基于边缘敏感的SLIC和二次密度聚类的GGO分割
2021-01-15陈晓楠王凯欣孙传恕刘晓凯毕京平
陈晓楠 王凯欣 孙传恕 刘晓凯 毕京平 彭 勇
1(大连海事大学信息科学技术学院 辽宁 大连 116026) 2(大连医科大学附属第二医院 辽宁 大连 116027) 3(大连理工大学水利工程学院 辽宁 大连 116024)
0 引 言
2019年1月,国家癌症中心发布的最新全国癌症统计数据显示,2015年全国的恶性肿瘤新发病例数达392.9万例,其中肺癌发病率占全国首位,发病病例高达78.7万[1]。肺癌已严重威胁到人们的生命健康。目前,CT(Computer Tomography)是早期肺癌检测中最为有效的医学影像检查手段之一[2]。随着科技水平的不断进步,医学影像切片的厚度越来越小,使得最终获得的切片数据量越来越大,导致放射科医生每天要阅读数以千计的CT图像,高的阅读量与诊断结果的准确率就产生了矛盾。为了尽量减少在前期由于主观因素而造成的漏诊、误诊现象,出现了计算机辅助诊断(Computer Aided Diagnosis,CAD)系统,CAD系统可以综合分析肺部医学图像,给医师提供“第二意见”[3]。
肺癌在早期一般表现为肺结节[4]。近年来,已有大量针对实质性结节分割算法的研究,而对磨玻璃型肺结节的分割方法中,如K近邻[5]、模糊聚类[6]、神经网络[7-8]、随机游走[9]等,都不能准确而高效地得到完整的GGO,且研究发现GGO的癌变率远远高于其他实质型结节。因此,研究GGO的分割对于肺癌的筛选和诊断具有更高的应用价值。
2003年,Ren等[10]首次提出超像素的概念,在近几年逐渐兴起,并成为目标识别、智能解释、目标跟踪、图像分割、人工智能等领域的研究热点。Achanta等[11]通过对目前超像素算法的比较分析提出一种简单有效的超像素分割方法——简单的线性迭代聚类(Simple Linear Iterative Clustering,SLIC)。该算法在区域紧密度、规则度以及算法的复杂度和准确率上都优于其他超像素方法,但在边缘贴和性上表现欠佳。DBSCAN是一种基于密度的空间聚类算法[12],该算法将达到一定密度阈值的块划分成多个区域,并在含有较多噪声或干扰的数据中找到相近的块并将其聚为一类,且可能由于GGO密度分布不均匀,导致一次密度聚类不能将其完整地分为一类。本文提出基于边缘敏感的SLIC和二次密度聚类的GGO分割方法,首先将边缘检测结果与SLIC相结合,改变初始聚类中心的选择标准,得到新的聚类中心,其次在传统密度聚类的基础上引入二次密度聚类的思想。实验结果显示,本文提出的算法具有较高的准确率和灵敏度。
1 算法原理及步骤
1.1 算法流程
本文在对含有GGO的图像进行分割之前,先对图像进行了预处理,去掉肺壁、衣物和机床等组织,得到肺实质轮廓。接着,对得到的肺实质进行边缘检测,将检测结果融入到SLIC产生的初始超像素块中,并且用区域质心代替其原始聚类中心,对图像进行过分割,然后对分割结果进行密度聚类,定位到GGO所在的簇,最后,对定位到的簇进行二次密度聚类,得到最终的GGO分割结果。算法的具体流程如图1所示。
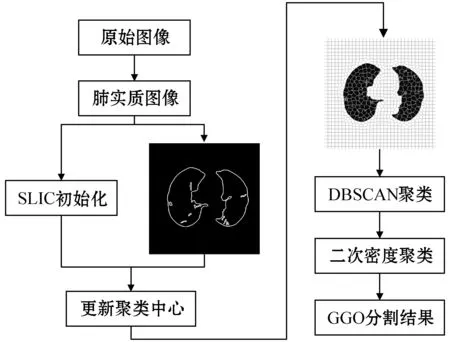
图1 系统总体流程
1.2 肺实质分割
由于医学图像的复杂性,在分割GGO之前,要将肺部区域分割出来,去掉无关的信息,例如肺壁、衣物、机床等。应用改进的区域生长和模糊C均值聚类相结合的方法分割肺区域,并用形态学的方法对区域边界进行修补。
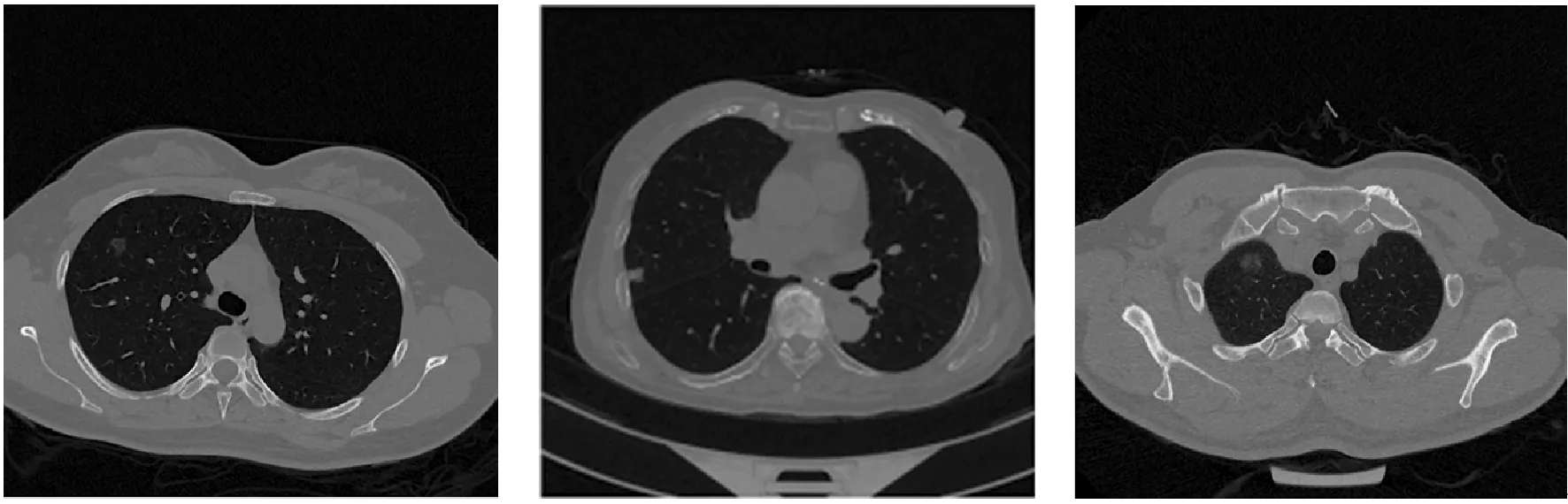
首先,将图像二值化,并根据二值化结果在含有最多空洞的区域中选择种子点,并选择此点作为生长的起点,进行自动区域生长并获得初始的肺实质轮廓。其次,由于轮廓边界具有模糊性,因此对初始轮廓进行边界展宽,且肺实质、肺壁、背景三部分具有较大的灰度差异,所以计算展宽的区域的灰度直方图,找到直方图的峰值,在展宽区域中选择对应峰值的像素点作为初始聚类中心,对图像进行聚类,得到肺实质。最后,为防止粘连肺壁组织对结果的影响,对聚类得到的肺实质用形态学方法进行边界修补。肺实质处理结果如图2所示。
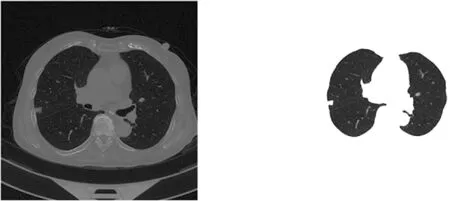
(a) 原始图像 (b) 聚类后图像
1.3 基于边界敏感的SLIC超像素分割算法
SLIC计算量较小且克服了以往算法产生的超像素数量不可控的缺点。SLIC将图像转化到CIELAB空间,并提取图像的五维特征向量V=[l,a,b,x,y],其中:[l,a,b]为像素颜色特征;[x,y]为位置特征。因此SLIC既考虑到了图像中像素之间颜色的相似性,又考虑到了位置的相近性。
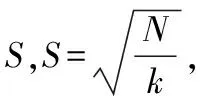
dc=(lj-li)2+(aj-ai)2+(bj-bi)2
(1)
ds=(xj-xi)2+(yj-yi)2
(2)
(3)
式中:dc和ds分别表示像素的颜色距离和空间距离;i表示聚类中心;j表示聚类中心搜索范围内的像素;m表示空间距离与颜色距离的权重系数,一般在1~40之间,值越大,分割后的超像素越紧凑,值越小,生成的超像素越不规则。
在SLIC初始化时,初始超像素块中如果包含图像边界,叫跨边界初始超像素,如果直接进行聚类,会产生跨边界超像素,此时超像素边界不会很好地贴合图像边界。跨边界超像素如图3所示。

图3 跨边界超像素
为了提高跨边界超像素的边界黏附性,提出基于边缘敏感的SLIC分割算法。该算法结合区域检测算子,判断初始超像素块是否为跨边界初始超像素块,若为跨边界初始超像素块,还需确保图像边缘与超像素块边缘形成闭合,若不闭合,则延长至距离最近的超像素块边缘使之闭合,用跨边界初始超像素的区域质心代替其原始的聚类中心进行聚类。新的聚类中心确定规则如下:
(1) 如果原始聚类中心的S×S搜索区域内存在图像边界,删除原始的聚类中心,并使边界与超像素块边界闭合,选择区域的质心作为初始聚类中心,如图4中的Bi。
(2) 如果原始聚类中心的S×S搜索区域内不存在图像边界,保留原始聚类中心不变,如图4中的Ci。
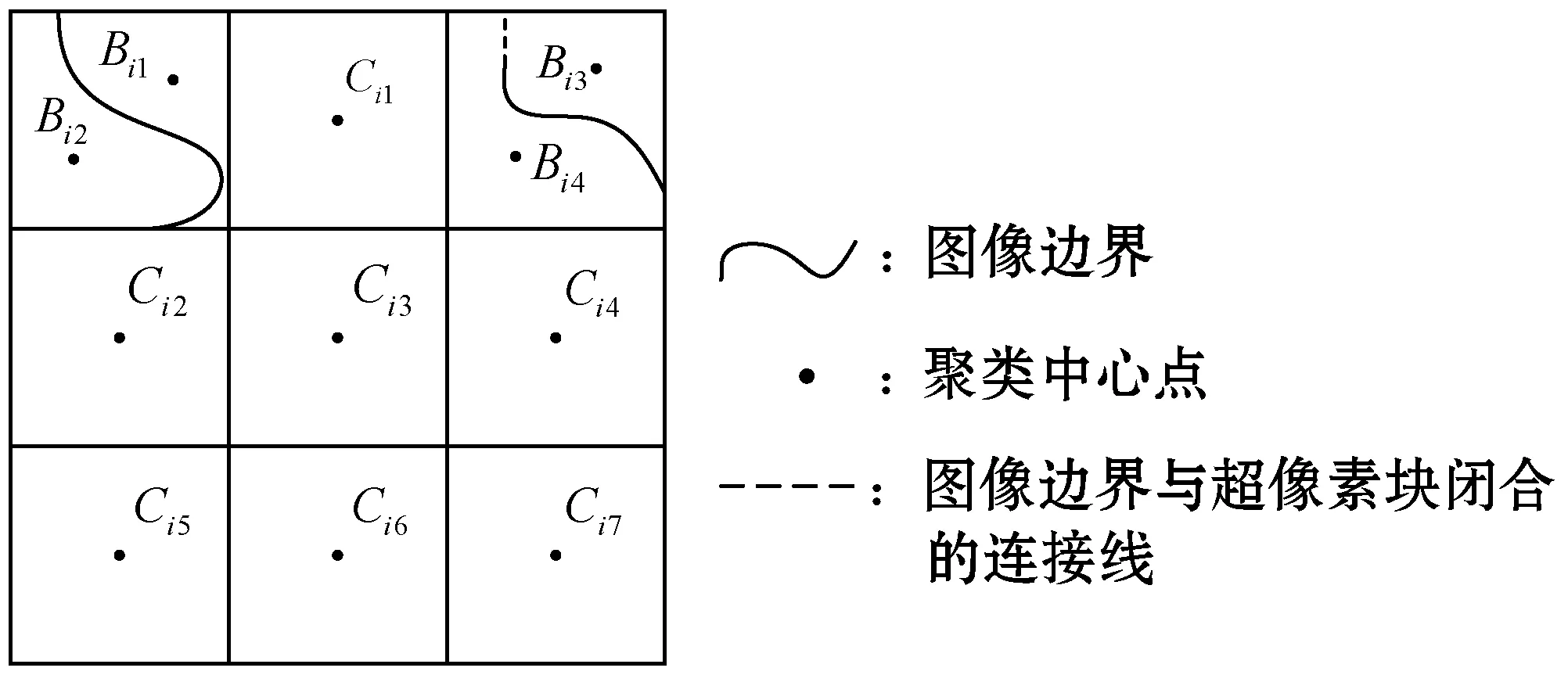
图4 聚类中心选择示意图
在分割算法中,需要根据k值,将图片划分为大小相等、排列整齐的超像素,本文选择k=1 000,因为此时的初始超像素块与GGO的大小最为相似,并选择每个超像素的中心点作为初始聚类中心。
对原始图像进行边缘检测时,本文选择LoG边缘检测算子,该算子克服了一般微分运算对噪声敏感的缺点。然后将检测得到的图像边缘和SLIC分割算法产生的初始超像素块相结合,更新原始的聚类中心,产生超像素过分割结果。
与传统的SLIC算法相同,选择聚类中心的2S×2S邻域,对属于该区域的像素进行搜索,通过计算像素与聚类中心的距离D,将每个像素归为距离相近的聚类中心。每当加入新的像素时,更新聚类中心为区域的均值,并重新计算新旧聚类中心的剩余误差。当剩余误差足够小时,迭代结束,删除此时面积过小的孤立区域,因为此时可能为血管干扰,并将其合并到相邻的超像素块中,得到最终的分割结果。
1.4 密度聚类算法
1.4.1DBSCAN算法分析
DBSCAN是一种基于密度的空间聚类算法,该算法通过引入密度可达的概念,将像素邻域内包含大于一定数量的点定义为核心点,相邻核心点直接密度可达,所有相互密度可达的点合并为一个簇,不属于任何一簇的点视为噪声数据,直到没有新的点添加到任何簇时,该过程结束。DBSCAN的几个重要概念:
(1) Eps邻域:以给定的对象为圆心,Eps为半径的区域,称为该对象的Eps邻域。
(2) 核心对象:若对象的Eps邻域内的样本个数不小于Minpts,那么对象为核心对象。
(3) Minpts:核心对象在其Eps邻域内包含的最小点数。
(4) 直接密度可达:样本中的两个点p和q,若p是核心对象,且q在p的Eps邻域内,则称p对q直接密度可达。
(5) 密度可达:对于样本集合C,给定一串样本点p1,p2,…,pn,p=p1,q=pn,若对象pi从pi-1直接密度可达,则对象q从对象p密度可达。
由于GGO与背景之间的对比度较低,且可能会存在密度不均匀的情况,使得在第一次密度聚类时,不能将全部的GGO包含在一类之中或GGO靠近边界的部分会和背景划分为一类,从而得不到完整的分割结果,因此本文提出一种二次密度聚类的方法。在第一次聚类后,根据超像素的类圆度、均匀度、密度小于血管的特性初步定位到GGO;根据邻域矩阵,只对定位到的GGO进行二次密度聚类,得到最终的结果。
1.4.2一次密度聚类
本文将DBSCAN聚类算法用于超像素而非像素[13]。将超像素作为核心对象,根据SLIC产生的超像素生成邻域矩阵,计算该超像素与其周围超像素之间的距离,若满足距离要求则将其合并到一个簇中,然后以新合并的超像素作为起点,重复上述过程,直到没有超像素加入到任何簇,得到聚类结果。由于经SLIC后产生的超像素块与其周围超像素块的距离相近,因此在第一次密度聚类计算距离时只计算颜色距离,计算公式如下:
d(i,j)=(lmj-lmi)2+(amj-ami)2+(bmj-bmi)2
(4)
式中:i、j为超像素;lm、am、bm为超像素三个颜色特征分量的均值。
经过聚类后,GGO仍然存在于含有实质的背景之中。因此,通过计算超像素的类圆度、标准差得到候选的GGO,然后根据GGO密度小于血管的特性得到GGO的精确定位。类圆度的度量标准如下:
(5)
式中:a是指目标的面积;p是指目标的周长。m越接近于1,则表示目标越接近于圆形。所以,候选GGO的确定规则如下:
(6)
式中:b为每个超像素的标准差;k为所有超像素中标准差的最小值。
选择其中z值最大的三个类作为GGO的候选,在候选的GGO中选择密度最小的区域,得到GGO的准确定位。
1.4.3二次密度聚类
针对第一次密度聚类时不能将GGO完整地分割在一个簇中的问题,本文提出二次密度聚类的方法,即在第一次密度聚类后,得到GGO的准确定位,以此超像素作为二次密度聚类的起始簇,只对该簇进行聚类。通过计算起始簇到其他簇的距离,根据阈值大小判断其他簇是否能够与起始簇合并。此外,要对第一次密度聚类后的图像要重新计算簇的邻域矩阵,确保满足阈值条件的簇为起始簇的邻域簇,否则,该簇不满足合并条件。采用五维特征向量来衡量两者之间的距离D′:
(7)
(8)
(9)
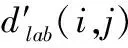
2 实 验
本文所用的含有GGO的肺部CT影像数据集均来源于大连医科大学第二附属医院。数据集中包含19个序列,每个序列平均包含300幅CT图像,所有图片的像素均为512×512,其中每幅包含有GGO的图像都由经验丰富的医生标注。实验平台为64位Windows 8操作系统,MATLAB R2016a,2.0 GHz处理器,4 GB内存。
本文提出将边缘信息融入到传统的SLIC算法中,并对跨边界初始超像素更新其聚类中心,本文算法与传统的SLIC分割结果对比图如图5所示。从图中可以看出,原始SLIC产生的超像素不能很好地贴和边缘,使产生的结果中含有无关信息,而本文提出的算法具有较好的边界黏附性。

(a) 传统的SLIC (b) 边缘敏感SLIC图5 SLIC和边缘敏感SLIC分割结果对比图
对于二次密度聚类的合并阈值,本文采用一种自适应阈值的方法。即通过计算第一次密度聚类得到的起始簇与其他簇的距离,对得到的距离大小进行排序,并绘制折线图,找到第一个斜率突变点。根据多次实验验证,选择阈值为30,即当不存在突变点或突变点大于30时,选择距离为30,否则选择突变点处的距离为合并阈值。距离排序后的折线图如图6所示,纵坐标表示起始簇与其他簇的距离,横坐标表示距离对应下每一个簇的密度聚类类别。
(a) 含有距离小于30的簇
图6(a)表示密度分布不均匀或靠近边缘区与背景对比度较低的GGO,此时,初始簇与邻域簇的差别较小,距离较近,根据自适应确定阈值的方法,此时的阈值为24.75。放大部分为第一个斜率突变点附近。图6(b)表示密度分布均匀的GGO,经一次密度聚类后能够得到完整的分割结果,因此与其他簇的距离较大,此时距离阈值设为30。放大部分为距离较小的前10个点。
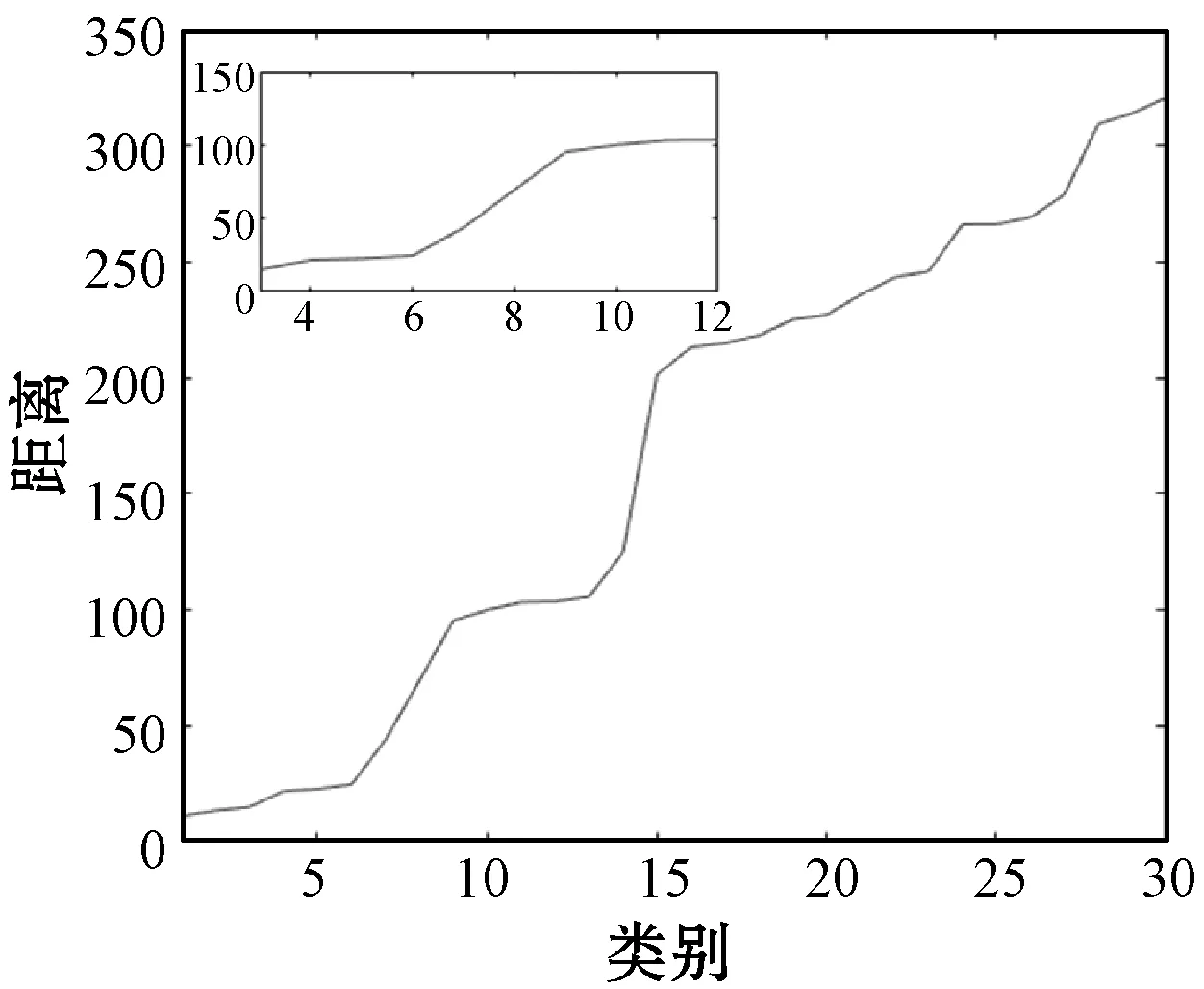
为验证本文算法的有效性,从影像数据集中随机抽取50幅含有GGO的图片进行实验,肺结节的部分处理结果如图7所示。
(a) 原始肺部图像
由图7(b)可以看出,经过预处理之后,图像中只剩肺实质部分,而与肺实质无关的组织(比如肺壁、机床以及患者衣物等)被去除,所以在进行超像素分割时,除肺实质外其他位置被视为背景,且被分割为接近标准的四边形。这样可以减少无关组织对于结果的影响。图7(d)为使用SLIC得到的结果,可以看出,由于原始SLIC边界黏附性较差,不融入边界信息的SLIC得到的结果会产生过分割或欠分割,得到的结果较差。图7(e)为密度聚类所得到的结果,由于GGO可能会存在局部密度不均匀,且边界与背景的亮度差异过小,使得在聚类时无法将完整的GGO聚为一个簇,所以要进行第二次密度聚类,以定位到的GGO为初始簇,只对该簇进行聚类,得到完整的GGO分割结果。
此外,要保证在第一次密度聚类后GGO边界区域不与背景划为一簇,要使第一次聚类的距离阈值尽量小,经过多次实验验证,第一次密度聚类的距离阈值设为8。图7(f)为本文算法分割得到的GGO,可以看出,本文算法能更加准确地得到GGO。
为了检测本文算法的准确率,采用准确率(Segment Accuracy,SA)和灵敏度(Sensitivity)作为算法的评价标准。将放射科专家手动分割结果作为评判的“金标准”,将“金标准”与本文分割算法所得到的结果进行对比,计算面积重叠度,得到算法的准确率[14]。准确率定义为:
(10)
式中:S1为本文算法的分割结果;S2为专家手动分割结果。SA的值越接近于1,代表分割准确率越高。
灵敏度的概念定义为将实际的结节像素点正确判断为感兴趣区域(金标准)结节像素点的比例。定义TP为检测出真结节的个数;FN为没有检测出真结节的个数,因此灵敏度可以表示为:
(11)
算法的交叉对比结果如表1所示,其中第一行为原始SLIC+DBSCAN算法所得结果,可以看出,该算法的准确率和灵敏度都较低;第二行为基于边缘敏感的SLIC+DBSCAN算法所得结果,可以看出,该算法灵敏度提高到了86%,比原始算法提高了24个百分点;第三行为SLIC+二次DBSCAN算法所得结果,可以看出,这种算法的准确率提高到了75.22%,比原始算法提高了19.05个百分点;第四行为本文算法,即基于边缘敏感的SLIC+二次DBSCAN,可以看出,该算法的准确率提高到了90.17%,比原始算法提高了34个百分点,灵敏度提高到了84%,比原始算法提高了22个百分点。
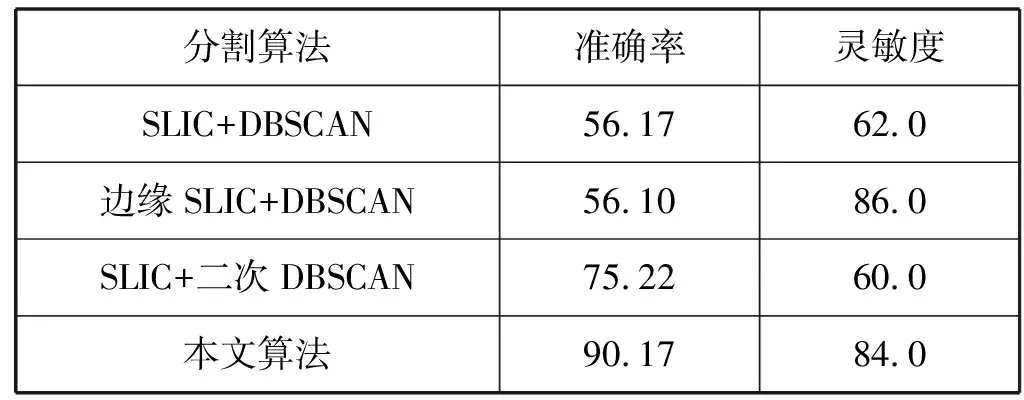
表1 算法准确率交叉验证结果 %
不同算法得到结果如表2所示,可以看出,本文算法的分割准确率和灵敏度均高于文献[15]提出的算法;与文献[6]所提出的算法相比,本文算法在灵敏度上虽然略低,但是在分割准确率上要远高于该算法。
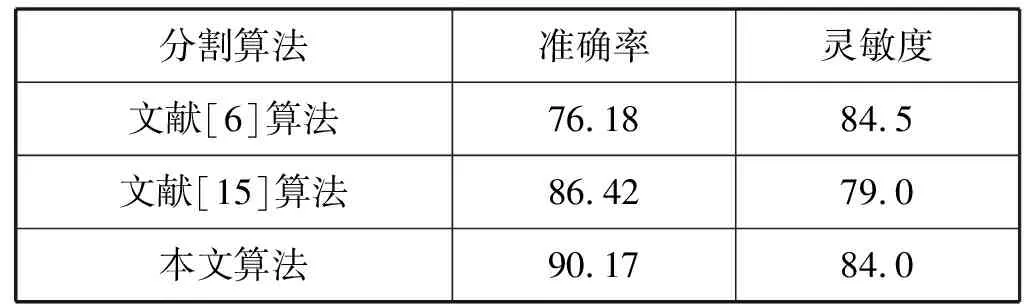
表2 算法准确率对比 %
3 结 语
本文提出一种基于边缘敏感的SLIC和二次密度聚类相结合的算法对GGO进行分割。针对传统的SLIC产生的超像素边界黏附性较差的问题,提出基于边缘敏感的SLIC,其分割结果能够很好地贴合边界,为后续的聚类奠定基础。随后,利用DBSCAN定位到GGO所在的簇,由于GGO可能会存在密度分布不均匀或边缘对比度过低等原因,导致在密度聚类后只得到部分GGO,为提高分割的完整性,提出二次密度聚类,只对GGO所在的簇进行聚类,得到完整的GGO。实验结果表明,本文算法能够更好地贴和图像边界且具有较高的准确率和有效性,在图像分割领域具有良好的应用前景。在实验过程中发现,孤立型GGO的分割准确率要高于肺壁黏连型GGO,下一步可针对孤立型GGO改进该算法模型。
