音圈电机直驱水液压球阀的动态特性建模与仿真研究

2021-01-14张增猛陈英龙

液压与气动 2021年1期

张增猛，王旭，杨勇，陈英龙，田昊

(大连海事大学船舶与海洋工程学院，辽宁大连 116000)

引言

直驱式电液伺服阀(Direct-Drive Valve，DDV)具有高频响应、结构简单等优点，是目前电液伺服阀的主要研究方向[1]。直驱式电液伺服阀在水液压领域的应用亦成为了研究重点。为准确地控制纯水液压系统中的压力或流量，直驱阀必须具有足够的控制精度和动态品质[2]。

近年来随着对环境友好性要求的提高，水液压技术发展取得了持续增长，水液压阀作为水液压系统的核心原件，广泛应用在煤矿水液压系统和海洋机电液装备中。国内外学者对水液压阀及其关键技术进行了广泛的研究。

刘晓鹏等[3]研制了一种音圈电机直驱高速水液压开关阀，实验结果表明直驱阀的流量可达100 L/min，在压力8 MPa、电压240 V的条件下，开启时间为7 ms，关闭时间为9 ms，动态特性较好。毛燕语等[4]研制了一种旋转式水液压比例阀，建立了其数学模型，并对其动态特性特别是频率响应进行了仿真研究。金铭[5]研制了一种伺服电机驱动式高压大流量水液压节流阀，仿真和试验结果表明该阀具有较好的位置控制精度和动态特性。白琼等[6]通过在Fluent中进行CFD仿真，分别研究了具有不同形式非全周阀口的水液压滑阀的液动力特性，结果表明水液压产生的液动力小于46#抗磨液压油产生的液动力。MAJDIC F等[7]在水液压三位四通滑阀阀芯上使用类金刚石涂层，循环寿命试验结果表明，此方法减小了水润滑条件下的滑阀摩擦力，改善了磨损和泄漏现象。周大伟[8]使用微造型技术改善了水液压三用滑阀的磨损现象。

本研究基于已研制的音圈电机直驱水液压球阀[9]，这是一种带有阀芯位移闭环的节流阀；经实验分析可知阀芯上各种作用力模型以及音圈电机模型不够准确是限制其动态特性提高的原因之一，而精确地建模是提高静态控制精度和动态响应效果的关键。对于阀芯上的作用力以及音圈电机模型，学者已进行了广泛的研究。

陈幼平等[10]自研了音圈电机并建立了数学模型，为了获取定量的黏性阻尼，对直线电机进行了自由振荡试验。YUAN Qinghui等[11]通过在Fluent中进行CFD仿真与试验研究了四边滑阀的稳态流体作用力，在分析滑阀流体作用力时使用了压力积分法与动量法，并指出在研究液动力时应当考虑流体黏性的影响。陈春等[12]对水液压伺服滑阀副之间的摩擦进行了实验研究，结果表明，Stribeck模型能较好的描述水液压滑阀副之间的摩擦力。

1 音圈电机直驱水液压阀的结构与数学模型

1.1 结构分析

音圈电机直驱水液压球阀的结构如图1所示。当音圈电机不通电时，阀芯通过两侧的弹簧定位使阀芯紧靠在阀座上。阀的最大设计流量为20 L/min，最大设计压力为4 MPa，阀芯位移为330 μm。流体由阀体6上的高压腔P流过阀套组件4进入阀腔，经球阀阀口后流入低压腔T，回到水箱。5为静压力平衡腔，可以平衡大部分的静压力。阀芯组件3由左推杆、球芯、右推杆组成；左推杆与音圈电机相连接，推动球阀阀芯与右推杆轴向移动，阀的出口流量与阀芯位移变化呈近似线性关系[9]。

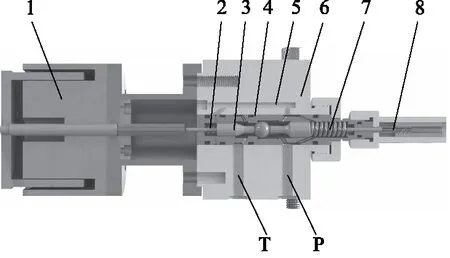
1.音圈电机 2.左弹簧 3.阀芯组件 4.阀套组件 5.静压力平衡腔 6.阀体 7.右弹簧 8.位移传感器

1.2 数学模型

阀芯上的作用力如图2所示，基于阀芯上的作用力关系建立阀芯动力学模型，如式(1)所示[13]：

1.陶瓷球 2.密封面 3.弹簧座

(1)

式中，Fem—— 音圈电机输出力

m—— 阀芯等效质量

x—— 阀芯位移

b—— 黏性阻尼系数

Ff—— 阀芯摩擦力

Fk—— 弹簧弹力

Fy—— 稳态流体作用力

Fo—— 密封圈阻力

1)音圈电机的数学模型

当音圈电机的结构和负载形式不同时，其数学模型也有差别[10]。本研究中将音圈电机动子的机械运动模型等效为一个单自由度的弹簧-质量-阻尼系统，如图3所示。

图3 音圈电机等效模型

由音圈电机的力平衡方程、电压平衡方程得到以x(t)为输出，u(t)为输入的音圈电机的微分方程进而拉氏变换得到音圈电机位移与控制电压之间的传递函数为：

(2)

式中，L—— 线圈电感

m—— 线圈质量

R—— 线圈电阻

k—— 弹簧劲度系数

km—— 电机力常数

2)流体作用力特性

阀内的流体对阀芯产生的液动力与静压力的合力称为流体作用力，流体作用力的存在影响阀的动、静态特性，是阀的设计中需要着重考虑的因素[14]。使用动量法来计算稳态液动力，从而可由式(3)计算阀芯上的流体作用力：

Fpoppet=pAp+Fy=pAp+ρQvcosα

(3)

式中，Ap—— 静压作用面积

ρ—— 水的密度，取998.2 kg·m-3

Q—— 流量

v—— 流束最小断面处的流速

α—— 流束方向与阀芯轴线的夹角，取45°

(4)

式中，A—— 阀口过流面积

Δp1—— 阀口前后的压差

Cd—— 控制阀流量系数，取0.95[15]

带入阀的参数，由动量法计算的稳态流体作用力数值如图4所示，由图可知，流体作用力随着压差和阀口开度的增大而增大，当压差为3.5 MPa，开口为330 μm 时，流体作用力达到最大值24.69 N。

图4 流体作用力数值

3)摩擦力模型

考虑阀芯与阀套之间的静摩擦力与动摩擦力，按Stribeck模型有：

(5)

式中，FS—— 阀芯静摩擦力

FC—— 阀芯库伦摩擦力

vs—— Stribeck速度

σ—— 黏性摩擦系数

4)密封圈阻力模型

O形密封圈的材料为丁腈橡胶，由文献[16]可知，其摩擦阻力可由式(6)计算：

(6)

式中，d—— 密封圈外径

B—— 密封圈宽度

f—— 摩擦系数，取0.2[17]

ε0—— O形圈预压缩量，本研究中为15%

E0—— O形圈的弹性模量

μ0—— O形圈的泊松系数

Δp2—— 密封圈两端的压差

根据以上分析，在Simulink中建立音圈电机输入电压与阀芯位移关系的模型，如图5所示。

图5 音圈电机直驱阀的模型

2 模型中的参数辨识

2.1 音圈电机黏性阻尼系数辨识

音圈电机的数学模型，其传递函数中的空气阻尼系数B未知，为辨识阻尼系数，设计搭建了带有弹性负载的音圈电机测试试验台，如图6所示。

1.弹簧 2.力传感器 3、5.直线轴承 4.音圈电机 6.LVDT传感器

带有弹性负载的音圈电机当外部作用力为0时，其力平衡方程为式(7)：

(7)

式中，m—— 运动部分质量

B—— 阻尼系数

k—— 弹簧劲度系数

将式(7)表示为典型二阶常系数齐次微分方程如式(8)所示：

(8)

即：

(9)

方程的左边完全由参数m，B，k所决定，反映了系统本身的固有属性；当电机进行初始振幅为A的自由振荡，得到电机的衰减振荡曲线方程式(10)：

x(t)=e-ntAcoskt

(10)

试验中，使用信号发生器输出正弦型号到功率放大器，功率放大器驱动电机实现振荡运动，待振荡稳定后，关闭信号发生器[18]，采集此时音圈电机位置信号随时间变化的振动曲线，并使用MATLAB拟合振动曲线为式(10)形式，如图7所示，辨识出空气阻尼系数为10.96 N·s/m。

图7 自由振荡曲线的拟合

2.2 阀芯摩擦力测量

为辨识Stribeck模型的关键参数，搭建试验台如图8所示，使用了步进电机带动滚珠丝杠推动阀芯，通过调节步进电机到一固定转速，就可以实现阀芯的匀速运动，此时不同运动速度下测量的轴向力就是阀芯与阀套之间的摩擦力。

图8 摩擦力测量试验台

将测量数值拟合为Stribeck函数，拟合结果如图9所示；经过拟合曲线得到参数：FC=0.6771 N，FS=1.65 N，vs=0.1276 mm/s，σ=0.3488 N·s/mm。

图9 摩擦力测量数值与拟合

3 动态模型的仿真分析

3.1 阶跃响应

通过辨识试验完善了直驱阀的Simulink模型，得到了线圈电压与阀芯位移之间的传递函数。

仿真时设置进出口压差为0.5，1.0，1.5，2.0，2.5，3.0，3.5，4.0 MPa，音圈电机最高电压输入电压为42.4 V，考虑到高压环境下阀芯上的阻力较大，因此分别选取音圈电机的阶跃电压为15，20，25，30，35，40 V。图10是稳态值的对比。图11～图13是选取了3组电压值和3组压差得到的阶跃响应曲线。

图10 阀芯位移的稳态值

图11 压差为0.5 MPa时的阶跃响应

图12 压差为2 MPa时的阶跃响应

图13 压差为3.5 MPa时的阶跃响应

由图可知：

(1)稳态值随着阶跃电压的增大而增大，随着进出口压差的增大而减小。当压差为3.5 MPa、阶跃电压为15 V时，稳态值最小为0.2234 mm；当压差为0.5 MPa、阶跃电压为25 V时，稳态值最大为2.196 mm；

(2)调整时间随着压差增大而增加，随着阶跃电压的增大有略微减小的趋势。当压差为0.5 MPa、阶跃电压为15 V时，调整时间最小为0.01654 s；当压差为3.5 MPa、阶跃电压为25 V时，调整时间最大为0.02225 s；

(3)阀芯位移的超调量随着压差增大而增大，随着阶跃电压增大几乎没有变化。当压差为0.5 MPa时，超调量最小为1.08%；当压差为3.5 MPa时，超调量最大为1.32%；

(4)上升时间随着压差的增大而缩短，随着阶跃电压的增大而缩短。当压差为0.5 MPa、阶跃电压为15 V时，上升时间最长为0.00854 s；当压差为3.5 MPa、阶跃电压为25 V时，上升时间最短为0.00533 s。

同时，压差增大，电机力需要补偿的轴向力越大，在图12、图13中阶跃响应曲线刚开始阶段位移为0反应了这一现象。

3.2 频率响应

本研究中直驱阀因为定位弹簧和密封圈的存在，音圈电机需要先抵消弹簧预紧力和密封圈的阻力才能推开阀芯，所以正弦响应的电压区间设置为6～16 V，频率为10 Hz，响应曲线如图14所示。由图可知，压差为0.5 MPa时，正弦响应幅值为1.016 mm；压差为1 MPa 时，正弦响应幅值为0.847 mm；压差为1.5 MPa时，正弦响应幅值为0.725 mm；随着压差的增大，正弦响应的幅值变小。