基于改进迭代贪婪算法的产品服务系统订单调度优化
2021-01-14高华丽
张 杨,但 斌,高华丽
(1.重庆工商大学 管理学院,重庆 400067;2.重庆市人文社科重点研究基地 重庆工商大学企业管理研究中心,重庆 400067;3.重庆大学 经济与工商管理学院,重庆 400044;4.西南政法大学 商学院,重庆 401120)
0 引言
近年来,由于产品同质化竞争的加剧、客户个性化需求的增加、生产要素成本的上升以及资源和环境问题的突显,全球制造业正在向信息化、智能化、绿色化和服务化转型升级。服务型制造作为创新发展的重要转型方向之一,得到了许多企业和国家的重视与推广。例如,IBM和罗尔斯·罗伊斯等公司从单纯的产品制造商成功转型为“产品+服务”解决方案提供商,全球500强企业中有两成跨国制造企业的服务收入超过总收入的50%。为了推动国家制造业的转型,德国推出了“工业4.0”,美国提出了“国家制造创新网络”,日本制定了“工业价值链”战略,这些国家战略均强调要推动服务型制造。2015年5月,国务院印发《中国制造2025》,提出“积极发展服务型制造和生产性服务业”[1]。2016年7月,工信部、国家发改委和中国工程院三部委联合印发《发展服务型制造专项行动指南》,提出到2018年“基本实现与制造强国战略进程相适应的服务型制造发展格局”[2]。在服务型制造模式下,制造企业将产品和服务整合为全面的解决方案,即产品服务系统(Product Service System, PSS)[3]。例如,在装备制造业(例如电梯、风电等行业),机械设备的生产与安装是一类典型的PSS。对于该类PSS订单,很多客户通常希望企业尽早交付,从而能够将PSS尽快投入使用以创造收益。例如,房地产开发商通常希望楼盘配套的电梯能尽早安装完毕,以加快新盘入市和资金回流;风电场业主通常希望风机能够尽早完成安装,以尽快实现并网发电创收。对于这类时间敏感型的客户,较短的PSS交付时间意味着更高的客户服务水平,同时也说明了企业具有更强的竞争力和更高的运营效率。这是因为在价格与质量相同或相近的情况下,客户通常会选择在更短时间内交付PSS的企业;从长期来看,PSS的交付时间越短,企业在单位时间内能够满足的PSS订单越多,收益就越多,同时对生产资源以及服务资源的利用率也就越高。因此,研究如何制定合理的PSS订单调度策略以实现订单的快速响应与交付,对于服务型制造企业提升服务水平和实现降本增效具有重要意义。
近年来,PSS得到了企业界和学术界的广泛关注与研究。许多学者采用定性方法对PSS的概念、设计和案例分析等内容进行了研究[4],然而仅有少量学者对PSS进行了定量研究,这些定量研究主要集中在市场博弈、合作契约分析和系统运作优化等方面。例如,Xie等[5]针对制造商和零售商合作提供PSS的供应链,在信息不对称条件下研究了3种协调契约对供应链决策的影响;Lee等[6]考虑单纯提供产品的传统渠道和提供PSS的服务化渠道间存在价格与质量竞争,基于博弈理论分析了服务依赖性和渠道可替代性对服务化竞争力的影响;刘宇熹等[7]针对租赁PSS设计了一种节约共享契约来协调再制造企业与客户间的收益。在运营管理领域,Li等[8]针对带有额外服务能力和面对不耐烦客户的PSS,构建了一种块结构的马尔可夫链优化模型;为了评估公共仓库的服务能力和优化资源配置,Cao等[9]采用目标分流法建立了一种仓库PSS服务能力成熟度模型;Wang等[10]针对同时提供产品与PSS的服务型制造系统,研究了最优生产和准入控制问题;王康周等[11]针对由生产设施和服务中心组成的柔性生产服务系统,研究了生产和服务能力的协同分配问题;Zhang等[12]基于物理互联网和PSS为云物流构建了智能箱型PSS,并结合云计算技术提出一种物流任务动态优化方法。上述文献为PSS的营销运营管理提供了经验和参考,然而这些文献均未探讨如何对几乎同时到达的批量PSS订单进行优化调度,该问题的本质是对PSS订单的生产任务和服务任务进行协同调度,因此目前亟待对PSS订单的调度问题进行深入探讨。本文的研究能丰富和拓展生产运营管理领域中调度管理和服务质量管理的相关理论与应用。
另一个与本文密切相关的研究方向是订单调度问题,该问题已成为生产与运营管理领域的研究热点。Wang等[13]考虑每个客户订单包含多个需要在不同专用设施上处理的作业,以最小化加权订单完成时间总和为目标研究了相应的订单调度问题;周水银等[14]针对流水车间环境,在服务水平约束下研究了成套订单的调度问题;梁旭等[15]针对加工和装配混合生产形态下的多订单调度问题,提出一种新的遗传算法;Xu等[16]提出一种基于位置学习效应的多订单调度问题,其优化目标设定为最小化总延误;为了解决具有准备时间的双代理多设施订单调度问题,Lin等[17]基于粒子群算法设计了3种元启发式算法;刘俨后等[18]针对混流装配线上的紧急插单情形提出一种动态调度策略,从而实现了紧急订单的最大程度交付和生产目标的最优化;Framinan等[19]针对最小化总延误的订单调度问题,提出了多种构造型启发式方法;Wu等[20]在客户订单调度问题中考虑基于加工时间的学习效应,并以订单总延误最小化为目标建立了相应问题的优化模型。上述研究仅考虑了单一生产类型或单一服务类型订单,而本文讨论的PSS订单调度问题同时包含了生产和服务的协同调度,情形更为复杂且难以求解。因此,以往针对单一类型订单调度问题的解决方案不适用于PSS订单调度问题,需要基于PSS的运作特点制定新的调度策略。
鉴于此,本文以拥有多条生产线和多支安装团队的服务型制造企业为对象,考虑客户在订单中规定了最早允许服务时间,对相应PSS订单调度问题进行研究。首先以最小化订单交付时间总和为目标构建问题的数学模型,然后根据问题特点设计改进的迭代贪婪(Interative Greedy, IG)算法进行求解,最后通过仿真实验分析算法的有效性。
1 问题描述
考虑拥有m条生产线M={1,2,…,m}和l支安装团队L={1,2,…,l}的服务型制造企业,面向市场满足客户的PSS订单需求,其交付流程如图1所示。在计划期的初始时刻即零时刻,企业接收了包含n个PSS订单的订单集合N={1,2,…,n}。其中,每个订单包含一单位的产品及相应安装服务,并规定了客户要求的最早允许服务时间,早于该时间客户会由于各种原因(如不具备安装条件)而不能接受服务。各PSS订单的交付需要依次经过生产阶段和服务阶段这两个阶段H={1,2},在生产阶段,企业需要决策各订单的生产任务分配给哪条生产线及各生产线上执行生产任务的顺序;在服务阶段,企业需要决策各订单的服务任务分配给哪支安装团队及各安装团队执行服务任务的顺序。企业的优化目标是通过制定最优的PSS订单调度策略,使得所有订单的交付时间总和最小化(等价于订单的平均交付时间最小化)。根据以上描述,在表1中给出了PSS订单调度问题的目标函数、输入条件、约束条件和输出条件,作为建立优化模型的基础。
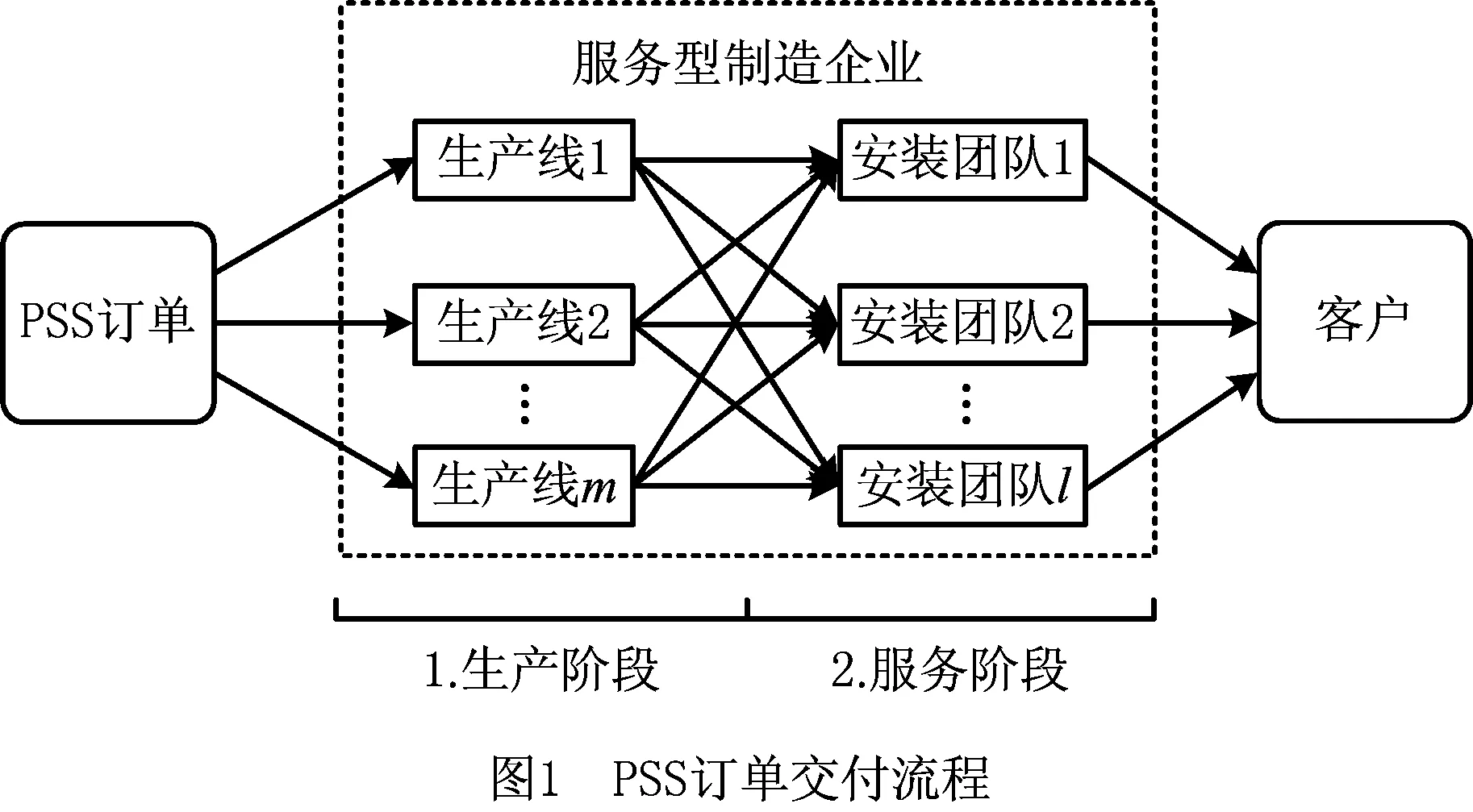

表1 PSS订单调度问题构成要素
本文研究的PSS订单调度问题的主要特点是:生产调度与服务调度的整合与协同。由于实物产品与服务具有不同的性质:产品是有形的、可储存的,而服务是无形的、不可储存的,因此在生产调度过程中,产品可以被提前生产并储存起来,并在后续时间成为提供服务的载体。这说明生产调度过程可以利用库存作为一种缓冲,从而能够在一定程度上保证产品供应的及时性。然而,服务的生产和消费是同时进行的,且服务的提供必须以产品为基础,因此服务调度过程不存在缓冲,而且会受到产品生产完工时间和最早允许服务时间的双重制约。由此可见,PSS订单调度中的生产调度和服务调度相互影响、相互作用,如何有效协同两种调度过程是企业面临的一个难题。此外,最小化订单交付时间总和的PSS订单调度问题属于NP-hard问题。如果不考虑最早允许服务时间的约束,将订单看作“工件”,同时将生产线和安装团队看作“机器”,则服务型制造系统可以看作是柔性流水车间(flexible flowshop)。而已知最小化加权完工时间的柔性流水车间调度是NP-hard问题[21],因此根据等价传递规则,本文研究的问题也是NP-hard问题。但在PSS订单调度问题中,由于服务具有不可储存性,生产完工后不能早于最早允许服务时间提供服务,这与多阶段生产系统可利用库存缓冲下一阶段的生产作业是不同的。PSS订单调度问题的上述特点和NP-hard特性使得该问题的求解非常困难,必须寻找协同和集中决策下的调度策略。
2 模型建立
2.1 模型假设
为了便于对PSS订单调度问题进行研究,本文假设:
(1)每个订单的生产时间和服务时间均是确定且已知的;
(2)同一订单在每条生产线上的生产时间均相同,在每支安装团队处的服务时间也相同;
(3)生产任务和服务任务一旦开始,不允许中断;
(4)同一时刻,每条生产线只能执行一项生产任务,每支安装团队只能执行一项服务任务。
2.2 符号定义
为了方便建立PSS订单调度问题的数学模型,定义如下符号:
(1)下标
i,j为订单序号;
k为生产线(安装团队)编号;
h为阶段类型,h=1表示生产阶段,h=2表示服务阶段。
(2)参数
pti为订单i的生产时间;
sti为订单i的服务时间;
ei为订单i的最早允许服务时间;
Q为足够大的正数。
(3)决策变量
STPi为订单i的生产开工时间;
CTPi为订单i的生产完工时间;
STSi为订单i的服务开始时间;
CTSi为订单i的服务完成时间;
yikh为如果订单i的生产(服务)任务被分配给生产线(安装团队)k,则yikh=1,否则yikh=0;
xijkh为如果订单i和j的生产(服务)任务被分配给生产线(安装团队)k,且订单i先于订单j,则xijkh=1,否则xijkh=0。
如果订单i∈N是生产线k∈M上第一个生产的订单,易知其最早生产完工时间等于生产时间pti。为使最早允许服务时间起到约束作用,需要求最早允许服务时间不早于其最早生产完工时间,即满足ei≥pti。
2.3 数学模型
基于上文描述和假设,构建PSS订单调度问题的数学模型如下:
(1)
s.t.
CTPi=STPi+pti,∀i∈N;
(2)
STPj≥CTPi+Q(xijk1-1),
∀i,j∈N,i≠j,k∈M;
(3)
STSi≥CTPi,∀i∈N;
(4)
STSi≥ei,∀i∈N;
(5)
CTSi=STSi+sti,∀i∈N;
(6)
STSj≥CTSi+Q(xijk2-1),
∀i,j∈N,i≠j,k∈L;
(7)
xijkh+xjikh≤yikh,

(8)
xijkh+xjikh≥yikh+yjkh-1,
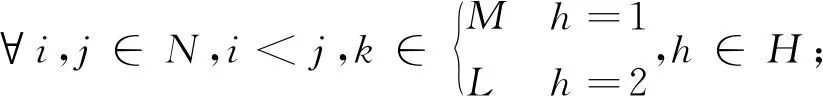
(9)
(10)
STPi≥0,CTPi≥0,STSi≥0,CTSi≥0,
∀i∈N;
(11)
xijkh,yikh∈{0,1},∀i,j∈N,

(12)
其中:式(1)表示目标为最小化订单交付时间总和;式(2)表示产品在生产过程中不允许中断;式(3)表示同一时刻每条生产线只能执行一项生产任务;式(4)表示同一订单的服务开始时间不能早于其生产完工时间;式(5)表示同一订单的服务开始时间不能早于其最早允许服务时间;式(6)表示服务在提供过程中不许中断;式(7)表示同一时刻每支安装团队只能执行一项服务任务;式(8)和式(9)表示每条生产线的生产任务执行顺序,以及每支安装团队的服务任务执行顺序;式(10)表示每个订单的生产任务必须被分配给一条生产线,服务任务必须被分配给一支安装团队;式(11)和式(12)定义了各决策变量的取值范围。
3 问题求解
最小化订单交付时间总和的PSS订单调度属于NP-hard问题,当规模较大时难以在多项式时间内获得精确解,因此通常采用启发式算法寻找问题的近似最优解。IG算法由是Ruiz等[22]提出的一种新型智能优化算法,该算法主要由邻域搜索、扰动算子和接受准则3个基本部分组成。IG算法提出后,以其参数少、易实现和效率高等特点引起了众多国内外学者的关注和研究,并在阻塞流水车间调度[23]和二次多重背包问题[24]等领域得到了理论研究和实践应用。
本文提出一种改进的IG算法来求解PSS订单调度问题,其基本思想为:首先基于订单的最早允许服务时间排序,设计一种构造型启发式算法来产生初始调度;然后采用局部搜索策略,在当前解的邻域内进行搜索和优化;局部搜索后,利用扰动算子跳出局部最优以防止算法过早收敛;最后,根据接受准则更新当前解和最好解,直到迭代满足终止准则。本文对IG算法的改进主要包括:①根据PSS订单调度问题的特点,提出了基于订单排列的整数编码与解码方法;②基于订单的最早允许服务时间排序,设计了一种用于产生初始解的构造型启发式算法;③基于变邻域搜索的思想,提出一种结合了插入和交换操作的高效邻域搜索策略;④在破坏和重建过程中,通过嵌入针对部分解的局部搜索优化提出了一种改进的扰动算子;⑤基于轮盘赌选择,设计了一种新的接受准则来更新当前解。下面对改进IG算法的主要部分进行说明。
3.1 编码与解码
本文采用基于PSS订单排序的编码方式对个体进行编码,个体的解可表达为π={π(1),π(2),…,π(n)},其中π(j)表示序列中排在第j个位置的订单。在对个体进行解码时,需要规定在PSS订单的交付过程中,不允许出现任何非强迫的空闲,即当生产线或安装团队处于空闲状态时,不存在可被立即执行的订单任务;此外,本文定义一个订单的“服务就绪时间”为该订单可以开始提供服务的最早时间,该时间一定不早于订单的生产完工时间和最早允许服务时间。个体的解码步骤如下:
步骤1在生产阶段,按照给定订单排序每次取出一个订单,将其生产任务分配给最先空闲的生产线,直到所有订单分配完毕;如果有多条生产线同时处于空闲,则将订单的生产任务分配给编号最小的生产线。
步骤2按照各订单的服务就绪时间对订单进行升序排列,从而得到一个新的序列;如果有多个订单的服务就绪时间相同,则将编号较小的订单排在前面。
步骤3在服务阶段,按照新的订单排列每次取出一个订单,将其服务任务分配给最先空闲的安装团队,直到所有订单分配完毕;如果有多支安装团队同时处于空闲状态,则将订单的服务任务分配给编号最小的安装团队。
步骤4各生产线和安装团队执行各自分配的任务,所有任务完成后,计算每个订单的服务交付时间。


表2 示例的订单参数

3.2 初始化
本文基于PSS订单的最早允许服务时间排序对NEH(Nawaz-Enscore-Ham)算法[25]进行改编,提出一种NEHEAST(NEH with earliest allowable service time)算法作为IG算法的初始化方法。该算法的基本思想如下:首先根据最早允许服务时间对订单进行升序排列,得到一个初始序列;然后对该初始序列前两个订单进行排序,选择具有较小订单交付时间总和的调度作为部分序列;接下来将初始序列中的剩余订单逐一插入到部分序列中的所有可能位置,并选择具有最小订单交付时间总和的调度作为新的部分序列;当所有订单插入完毕,最后重新得到一个完整序列。NEHEAST算法的伪代码如图3所示。

3.3 邻域搜索
邻域搜索方法对IG算法的求解效果影响很大。经典IG算法采用的邻域搜索方法是一种基于插入操作且首次改进即更新的高性能局部搜索算法,该算法能够找到基于插入邻域的局部最优,但是忽略了交换邻域这种常用的邻域结构,而关于插入邻域的局部最优解不一定是关于交换邻域的局部最优解。因此,受Solis等[26]提出的随机搜索(random search)以及Hansen等[27]提出的简化变邻域搜索(reduced variable neighborhood search)思想的启发,本文将插入邻域搜索和交换邻域搜索相结合,提出一种随机邻域搜索(Random Neighborhood Search,RNS)算法,以扩大搜索空间和提高寻优效率。其基本思想是:每次从当前解中随机地选择一个订单,随机地选择插入邻域或者交换邻域进行搜索,前者将其从原位置移除并插入到所有可能位置中的最优位置,后者将其与所有可能位置中最优位置的订单进行交换;如果通过邻域搜索找到的新解优于当前解,则替换当前解并且继续搜索,否则结束搜索。随机邻域搜索的伪代码如图4所示。

3.4 扰动算子
为了避免IG算法在求解PSS订单调度问题时陷入局部最优,必须设计一种有效的跳出机制,该机制也称为扰动算子。经典IG算法采用破坏(destruction)和重建(construction)过程作为扰动算子,其主要思想是:在破坏阶段,从当前解中随机选择若干订单并移除,得到两个部分序列:由剩余订单组成的部分解、由移除订单按照移除顺序组成的部分序列;在重建阶段,将部分序列中的订单逐一插入到部分解中所有可能位置的最优位置,从而最终得到一个扰动解。然而,该扰动算子在扰动后,可能丢失局部最优解的优良特性,从而导致后续局部搜索可能陷入比之前局部最优解更差的局部最优点。Framinan等[28]以及Rad等[29]的研究表明,在构造完整解的过程中对部分解进行邻域搜索优化能够改善最终解。受上述研究的启发,本文提出一种破坏—优化—重建(Destruction-Optimization-Construction, DOC)作为改进IG算法的扰动算子,其主要创新在于:对执行破坏操作后的部分解实施若干次插入邻域搜索,再对优化后的部分解执行重建操作,以期改善扰动解的质量。DOC扰动算子的伪代码如图5所示。

3.5 接受准则
接受准则的作用是更新IG算法的当前解和最好解。然而,由于扰动算子的扰动有时可能不是足够大,导致算法在后续局部搜索过程中又陷入到相同局部最优点。为了帮助IG算法更有效地跳出局部最优,本文基于遗传算法中常用的轮盘赌选择(Roulette Wheel Selection,RWS)策略,提出一种新的接受准则。在该接受准则中,需要构建一个精英表(elite list),该精英表储存了通过局部搜索找到的新解。
RWS接受准则:通过局部搜索找到新解后,如果新解优于最好解,则更新最好解,且清空精英表;如果新解不在精英表中,则将新解添加到精英表的尾部;如果精英表的长度超过ω,则从表中删除最坏解;按照RWS策略从精英表中选择一个解为当前解。令精英表的长度为τ(τ≤ω),RWS策略的实现步骤如下:
步骤1对精英表中每个解的目标值进行min-max归一化处理,计算公式为:


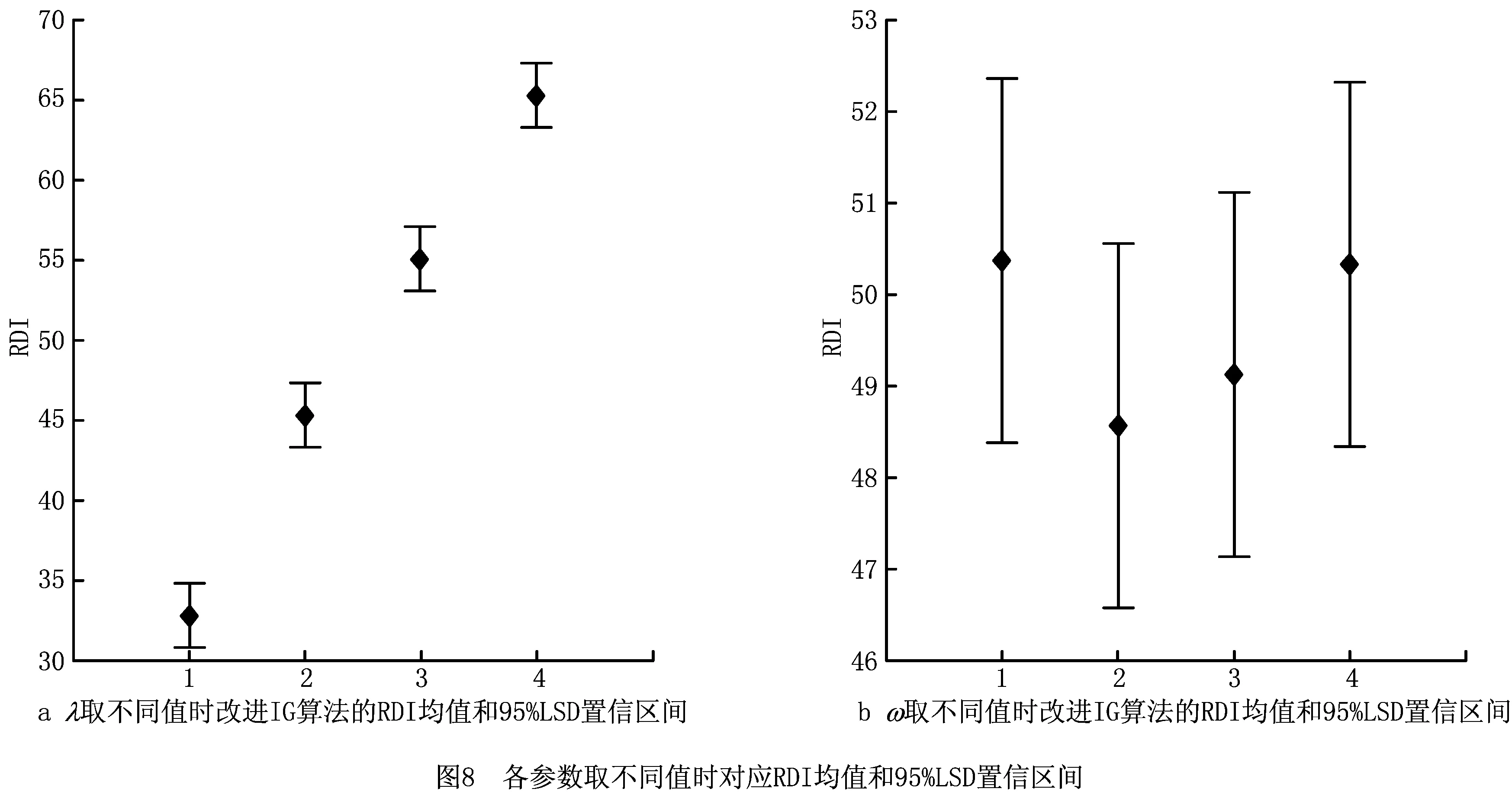
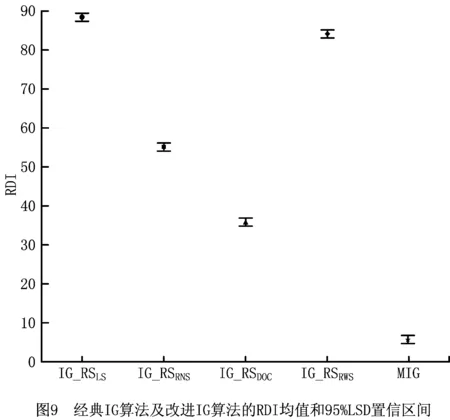
步骤3由[0,1]区间的均匀分布产生一个随机数Rand。如果Rand RWS接受准则的伪代码如图6所示,其中π和π*分别表示当前解和最好解,EliteList表示精英表。 Procedure RWS(π,π*,EliteList,ω) if Z(π) π*:=π; EliteList:=∅; end if if π∉EliteList then add π to the end of EliteList; end if if |EliteList|>ω then remove the worst solution among EliteList; end if π:=a permutation selected from EliteList according to the RWS strategy; return{π,π*,EliteList} end procedure 图6 RWS接受准则的伪代码 由于具有较大订单规模的PSS订单调度问题可能需要运行更长时间来搜索最优解,本文设置改进IG算法的终止条件为最大CPU时间100nms,该终止条件能够随着订单规模n动态地调整。 结合PSS订单调度问题的特点,上文对改进IG算法的主要组成部分进行了描述,如图7所示为整个算法的求解流程。 Procedure MIG set the parameters λ and ω; π0:=NEHEAST; π:=RNS(π0); π*:=π; EliteList:={π}; while CPU time≤100n do π′:=DOC(π,λ) π″:=RNS(π′) {π,π*,EliteList}:=RWS(π″,π*,EliteList,ω); end while return π* end procedure 图7 改进IG算法的求解流程 本章通过仿真实验来评价改进的IG算法的优化性能。所有算法均采用MATLAB(R2018b)编制程序,并在一台配备2.50 GHz Intel(R)Core(TM)i5-7300HQ CPU和8 G RAM的PC机上进行实验。 根据PSS订单调度问题的特点,考虑随机产生测试算例。令生产时间pti和服务时间sti均由区间[1,100]的均匀分布随机产生,最早允许服务时间ei由区间[pti,(1+θ)pti]的均匀分布随机产生。算例的实验参数取值为n={50,100,150,200}、m={2,5,10}、l={2,3,5}和θ={1,2,3},故共有4×3×3×3=108种参数组合。对于每种参数组合,随机产生2个算例,这样可得到一个包含108×2=216算例的基准测试算例集。 评价算法性能的指标为相对偏差指数(RDI), 其中对于每个算例,Zalg表示给定算法得到的订单交付时间总和,Zbest和Zworst分别表示所有算法得到的订单交付时间总和的最小值和最大值。如果Zbest与Zworst相等,表示所有算法得到的订单交付时间总和均相同,此时令RDI的值为零。RDI的值越小,说明给定算法的性能越好。 算法的参数设置对求解效果有重要影响,因此本节采用实验设计(design of experiments)[30]方法对改进IG算法的参数进行调整。Pan等[31]指出,将参数校准的基准算例与最终测试的基准算例分离是至关重要的,因为采用最终测试的基准算例进行参数校准会造成过度校准和产生过于乐观的结果,算例一旦改变将导致算法无法再获得好的计算结果。据此,本文用于参数设置的算例集合包含50个算例,每个算例通过随机选取n′={20,50,80,100,120,150,180,200}以及上述m、l和θ的参数取值集合中的一个值来产生。 在实验设计方法的因子设计中,考虑将算法参数看作因子,并对因子的不同水平进行测试。改进IG算法包含两个参数:λ和ω,测试水平分别为:λ={1,2,3,4}和ω={5,6,7,8},这样共有4×4=16种参数组合。对于每种参数组合,改进IG算法分别对每个算例运算5次,并对计算结果取平均值。 参数设置的实验结果采用双因素方差分析(ANalysis of VAriance,ANOVA)技术进行分析。采用ANOVA进行统计分析需要满足3个基本假设:正态性(normality)、方差齐性(homogeneity of variance)以及独立性(independence),实验数据的残差分析表明这些假设均是有效的。改进IG算法的ANOVA结果如表3所示。根据统计学理论,F值越大,则对应因子的影响就越显著,P值给出了对应因子的最小显著性水平,P值小于0.05表明对应因子的影响是显著的。由表3可见,参数λ对改进IG算法性能的影响在统计学意义上是显著的,但是参数ω对算法性能的影响并不显著。此外,参数λ和ω之间的交互作用对改进IG算法性能的影响也不显著。 表3 改进IG算法参数设置实验的ANOVA结果 为了更好地分析参数λ和ω对改进IG算法性能的影响,图8给出了各参数取不同值时对应RDI均值和95%LSD(least significant difference)置信区间。根据统计学理论,如果其他因子在不同水平下的置信区间不重叠,则可认为该因子在不同水平下的效果有显著区别。由图8a可见,随着参数λ取值的增大,改进IG算法的性能显著下降,参数λ取值为1要显著优于取值为2、3和4。图8b表明参数ω取不同值时并未产生统计意义上的显著差异,但改进IG算法的平均性能在参数ω取值为6时要略优于其取值。因此,根据改进IG算法参数设置实验的ANOVA结果,改进IG算法的参数可以设置为λ=1和ω=6。 为了检验改进IG算法的有效性,将其与经典IG算法(记为IG_RSLS)[22]进行对比分析。首先对经典IG算法进行改编,以适应求解PSS订单调度问题的需要,包括编码和解码方法、初始解产生方法和终止条件均采用本文提供的方法,以保证对比的公平性;但是经典IG算法中的局部搜索方法、扰动算子和接受准则这3个主要组成部分均保留不变。基于经典IG算法,分别采用本文所提改进策略对上述3个主要组成部分进行改进,从而得到3种部分改进的IG算法,分别记为IG_RSRNS、IG_RSDOC和IG_RSRWS。将经典IG算法、3种部分改进的IG算法和完整改进的IG算法作为参与比较的算法,以分别检验每种改进策略的有效性。分别采用上述5种IG算法求解基准测试算例集,每个算例运算5次。 基于实验数据,绘制各个IG算法的RDI均值和95%LSD置信区间,如图9所示。由图9可见,IG_RSRNS、IG_RSDOC和IG_RSRWS算法的RDI均值分别领先IG_RSLS算法约38%、60%和6%,表明DOC扰动算子对经典IG算法性能提升的改进效果最好,其次是RNS局部搜索算法,最后是RWS接受准则;此外,这些改进IG算法的优化性能均优于经典IG算法,表明本文所提出的RNS局部搜索算法、DOC扰动算子和RWS接受准则3种改进策略都是非常有效的。特别地,MIG算法的RDI均值相比IG_RSLS算法领先了约94%,表明MIG算法的改进是非常成功的;而且,MIG算法的求解效果相比IG_RSRNS、IG_RSDOC和IG_RSRWS算法都要好,说明本文所提出的各种改进策略之间具有较好的兼容性和协同性。 为了考察MIG算法对算例的关键参数n、m、l和θ的敏感性,图10~图13分别描述了MIG算法关于这些参数的变化趋势。由图10可见,随着订单规模的增大,MIG算法的RDI均值逐渐下降,而IG_RSLS算法的RDI均值却逐渐上升,表明在求解较大规模的PSS订单调度问题时,改进IG算法相比经典IG算法更有优势。由图11和图12可见,生产线数量和安装队数量的变动对MIG算法性能的影响较小,表明MIG算法对这两个算例参数具有较好的鲁棒性。在图13中,参数θ的值越大,意味着各订单的最早允许服务时间越分散。图13同样表明,MIG算法的性能对于最早允许服务时间的波动同样具有较好的鲁棒性。 上述实验结果表明相比经典IG算法,MIG算法在求解各种规模(尤其是较大规模)和不同特征的PSS订单调度问题时具有更好的性能和较好的鲁棒性,因此可以作为决策者解决此类问题的有效求解工具。 本文针对拥有多条生产线和多支安装团队的服务型制造企业,考虑客户规定订单交付的最早允许服务时间,以最小化所有订单交付时间总和为目标构建了PSS订单调度问题的数学模型,并根据问题特点设计了求解问题的改进IG算法。该算法的主要创新在于:开发了一种高效的随机邻域搜索算法作为局部搜索方法,提出了一种破坏、优化与重建过程作为扰动算子,并基于轮盘赌的选择策略设计了一种新的接受准则。通过仿真测试验证了IG算法改进策略的有效性,并分析了关键参数对算法性能的影响,发现改进IG算法不但性能优异而且具有较好的鲁棒性。本文的研究可以为服务型制造企业的PSS订单调度决策者提供高效的优化建模与求解工具,从而有助于企业提高客户服务水平和实现降本增效。未来可进一步研究具有多个优化目标的PSS订单调度问题,以及如何设计更加有效的元启发式算法对相关问题进行求解。3.6 终止条件
3.7 求解PSS订单调度问题的改进IG算法流程
4 仿真实验
4.1 算例构造与性能评价指标
4.2 实验参数设置

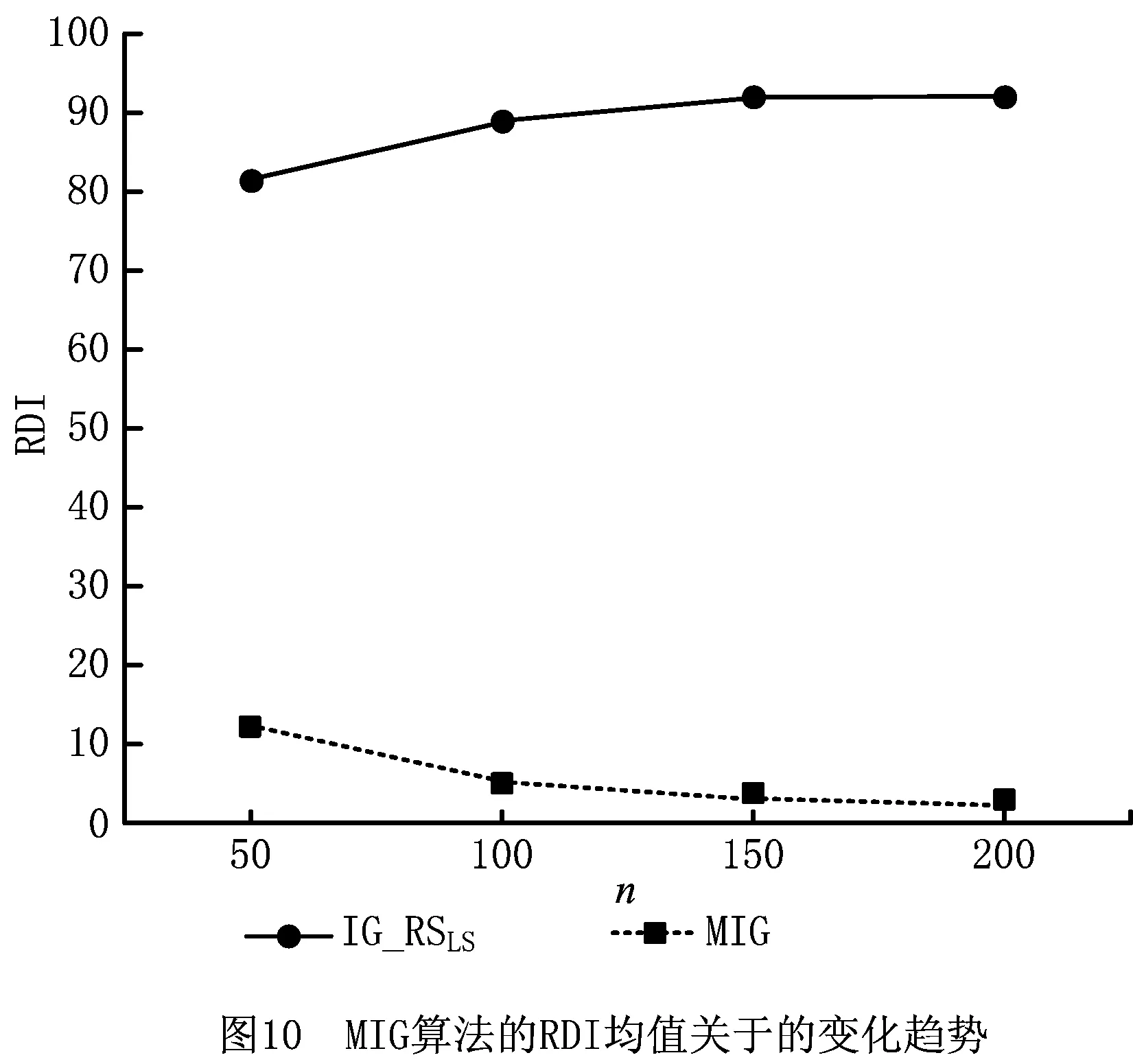
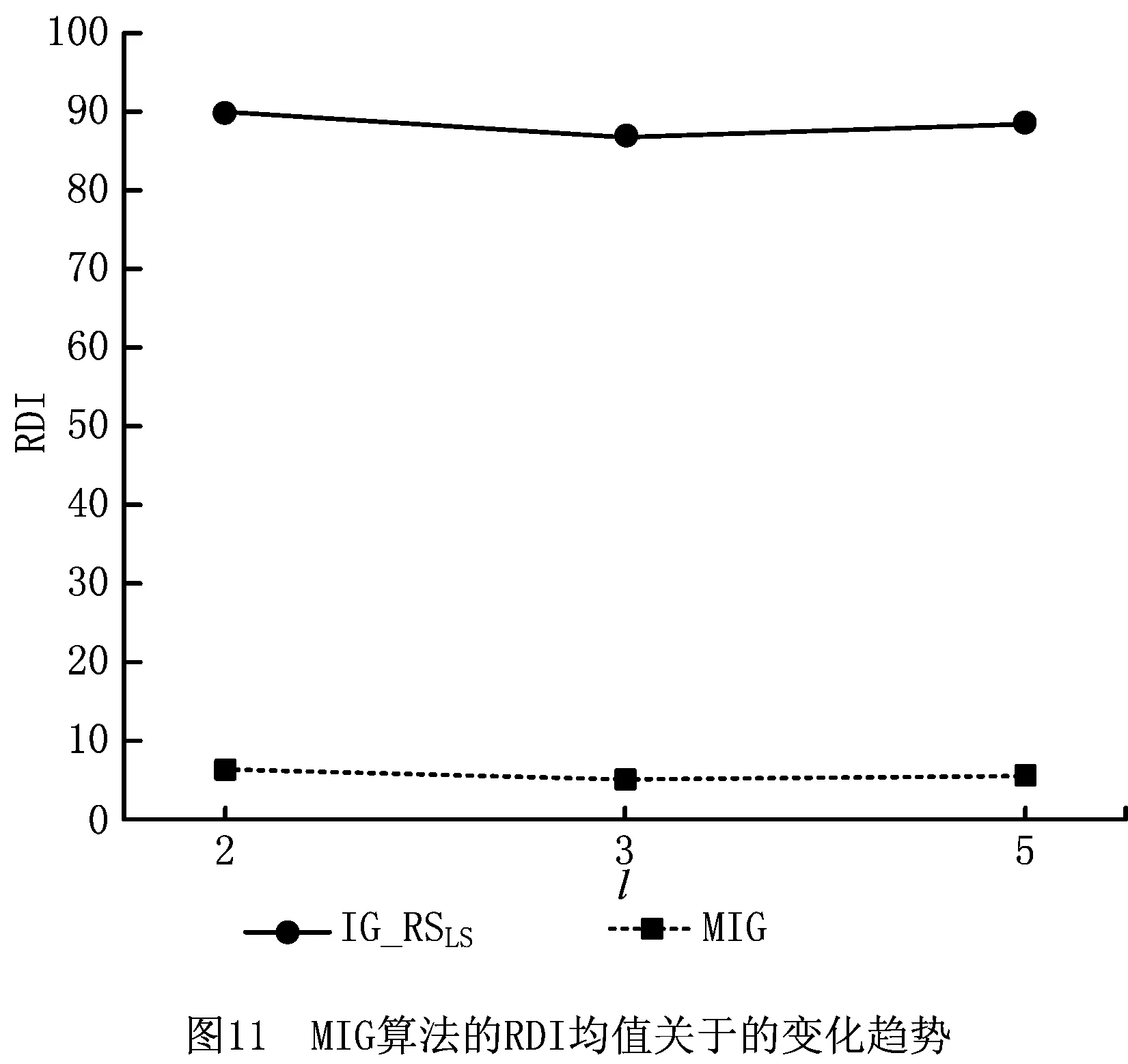
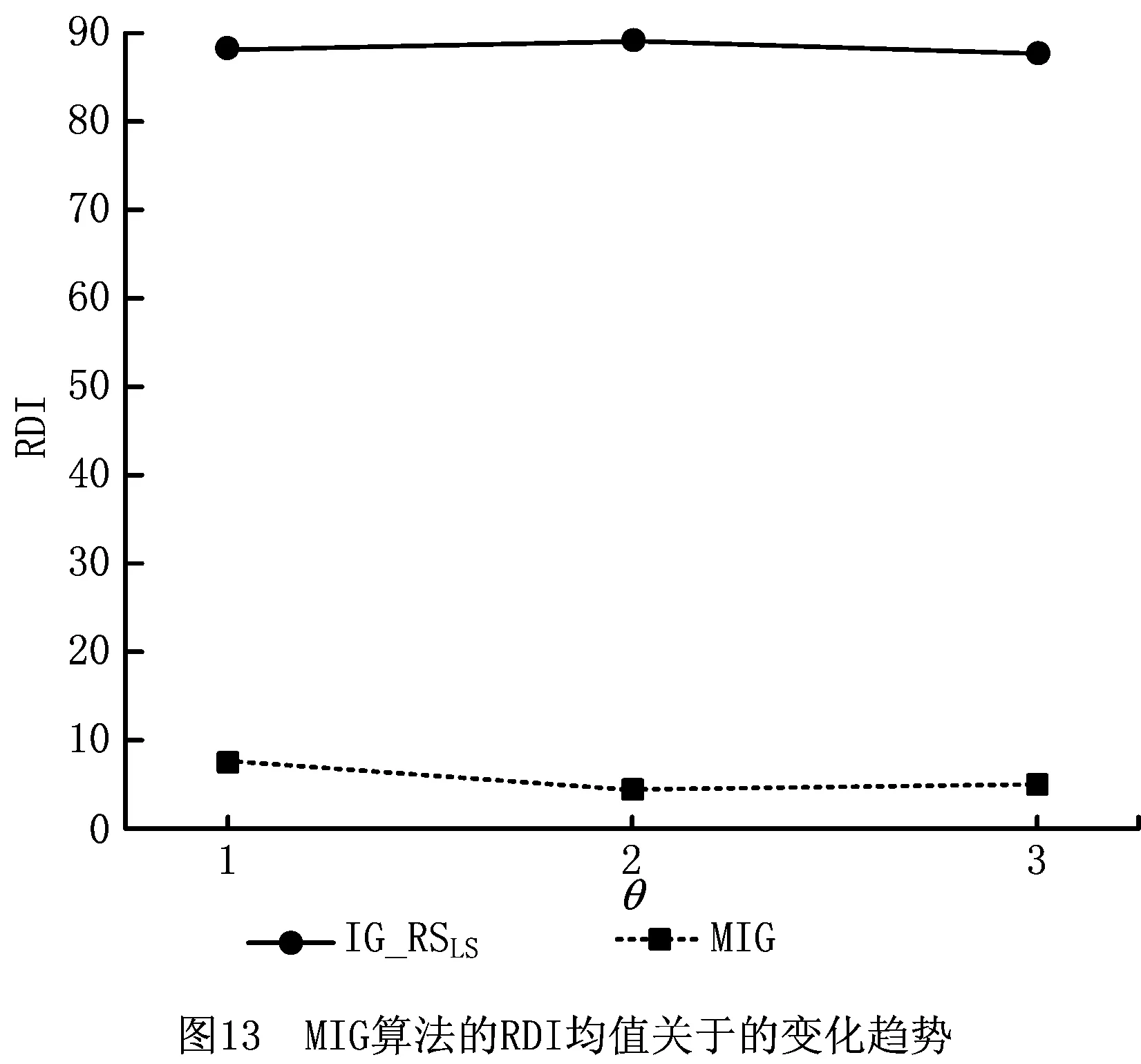
4.3 改进IG算法的有效性与鲁棒性分析

5 结束语
