面向宏观工艺重用的三维CAD模型检索方法

黄 波，张树生+，黄 瑞，李秀玲,3，梁嘉宸

(1.西北工业大学 现代设计与集成制造技术教育部重点实验室，陕西 西安 710072；2.河海大学 物联网工程学院，江苏 常州 213022；3.郑州铁路职业技术学院 实践教学中心，河南 郑州 450052)

0 引言

目前，数控加工工艺设计虽然应用了功能强大的计算机辅助制造(Computer Aided Manufacturing, CAM)系统，但在工艺分析和决策的各个层面，仍非常依赖工艺设计人员的知识和经验，导致数控加工的工艺准备周期长、工艺设计智能化程度低等突出问题。据某飞机主机厂统计，在航空关重件的数控加工过程中，超过70%的时间花在工艺分析和交互编程上，而数控机床的有效加工时间则不到30%。另一方面，大量的加工工艺数据(本文主要指三维计算机辅助设计(Computer Aided Design, CAD)模型及其关联的数控工艺)在产品制造过程中不断地积累，蕴含了设计人员丰富的工艺知识、意图和经验[1]。据统计分析，在新产品开发中，设计人员通常通过修改或者直接重用相似实例来进行新产品的设计，而相同模式也存在于产品的数控加工工艺设计阶段[2]。因此，如何快速准确地获取相似的零件，并对其携带的制造信息进行重用，是提高产品开发效率和质量、缩短产品开发周期急需解决的问题。

在工艺数据中，宏观工艺过程作为工艺设计人员对零件整体加工工艺的综合分析结果，能够有效地反映零件的整体拓扑结构、关键制造特征以及精度要求，其蕴含了丰富的高层次工艺设计意图，使得它对零件的整个加工过程具有指导性作用[3-4]。因此，工艺数据中内含的宏观工艺过程具有巨大的重用价值。近年来，基于内容的三维CAD模型检索技术的出现，为相似零件的精细发现与工艺数据的有效重用提供了一种新的使能手段。然而对于面向宏观工艺重用的三维CAD模型检索来说，查询到整体都符合检索需求的模型并进行重用的情况较少。另一方面，针对零件整体的三维CAD模型检索研究已得到广泛关注并取得丰富研究成果。Ramesh等[5]通过体分解方法识别零件三维模型的加工特征，通过加工特征的类型、方向、数量等7个特征量的比较对模型进行相似性评价。Cardone等[6]将三维模型相似性评价用以支持零件的加工成本估算，引入了加工特征的走刀和进给方向等，以反映装夹次数等与工时估算相关的因素。Zhang等[7]提出一种基于产品综合信息模型的机械零件相似性评价方法。该模型集成了几何信息与非几何信息，以达到更好的模型识别与分辨能力，通过对这些信息的比较可以有效地实现模型间的相似性评价。You等[8]针对汽车面板加工提出一种面向冲压工艺规划与模具设计的几何相似性评价方法。Li等[9]提出一种面向模具数控加工刀具序列重用的相似几何检索方法，该方法通常适用于具有对称面的特殊曲面。但是这些方法仍是以三维几何相似性为前提，难以保证检索结果关联工艺的可重用性，还需设计人员进一步甄别其重用价值。

为了解决上述问题，本文提出一种面向宏观工艺重用的三维CAD模型检索方法，以支持数据驱动的工艺设计模式。该方法的创新点概括如下：①引入工艺骨架将工艺数据实例进行基于宏观工艺的结构化表示，提高了在线检索过程的效率；②采用概率统计方法构建查询零件中制造特征与宏观工艺的关联映射关系，不是对已制零件的逐一匹配，而是相似零件族驱动，检索过程具有较好的柔性；③以工艺骨架为驱动，从可加工区域角度出发评估查询零件与工艺数据实例之间的整体相似度，检索结果可以保证其关联工艺的可重用性，无需设计人员进一步甄别其重用价值。

1 基本概念与方法概述

1.1 基本概念

定义1宏观工艺重用。区别于微观工艺重用对制造特征/局部结构的加工方法、加工策略以及加工参数等微观工艺参数的重用，宏观工艺重用则是在三维CAD模型检索结果的基础上，进一步从已有的相似零件族实例中挖掘共有的核心宏观工艺，即工艺骨架，从而实现对工序/工步、时序关系、刀具、加工余量等宏观工艺信息的快速重用，取代或基本取代交互式工艺分析过程。宏观工艺重用为对相似零件族的共有核心宏观工艺的继承操作，具体可以表示为

∀PC(GPs,PS),P(GP),

其中：PC为零件族；P为待制零件；GP表示零件的三维几何信息及精度要求，包括制造特征、公差、表面粗糙度等；PS为工艺骨架；f为宏观工艺重用操作函数，本文中对应为后续的关联映射关系；π(NP(GP),NP(GP,PS))表示在f的作用下，待制零件继承可重用宏观工艺后的状态，即在宏观工艺的驱动下将零件三维几何划分为可加工区域集合；MR表示可加工区域；→表示并行加工顺序，·表示串行加工顺序。

定义2基于制造特征的结构化CAM模型(Feature-based Structured CAM model, FSCAM)。FSM是由制造特征F、局部结构C、加工操作Op、工步WS以及工序WP构成的树型层次结构，可表示为FSCAM::=({F|C|Op|WS|WP},R)。其中R为该结构化模型中的关系集合，包括加工关系RM、时序关系RT、父子关系RP和耦合关系RC。

如图1所示为一个工艺数据实例结构化后的FSCAM模型，包括6个孔(如H1，H2)，3个凸台(如B1，B2)，16个型腔(如P1，P2)，构成了9个局部结构(如C1，C2)。同时，包含了116个加工操作(如型腔铣Po1，轮廓铣Pf1)，构成了10个工步(如精铣型腔底面D32FPB)，3个工序(如粗加工Roughing)。由图1可知，父子关系构成了树形层次结构，而耦合关系描述了制造特征间的相互作用，从而反映特征间的加工顺序。加工关系和时序关系共同描述了零件中特征的加工形成过程。

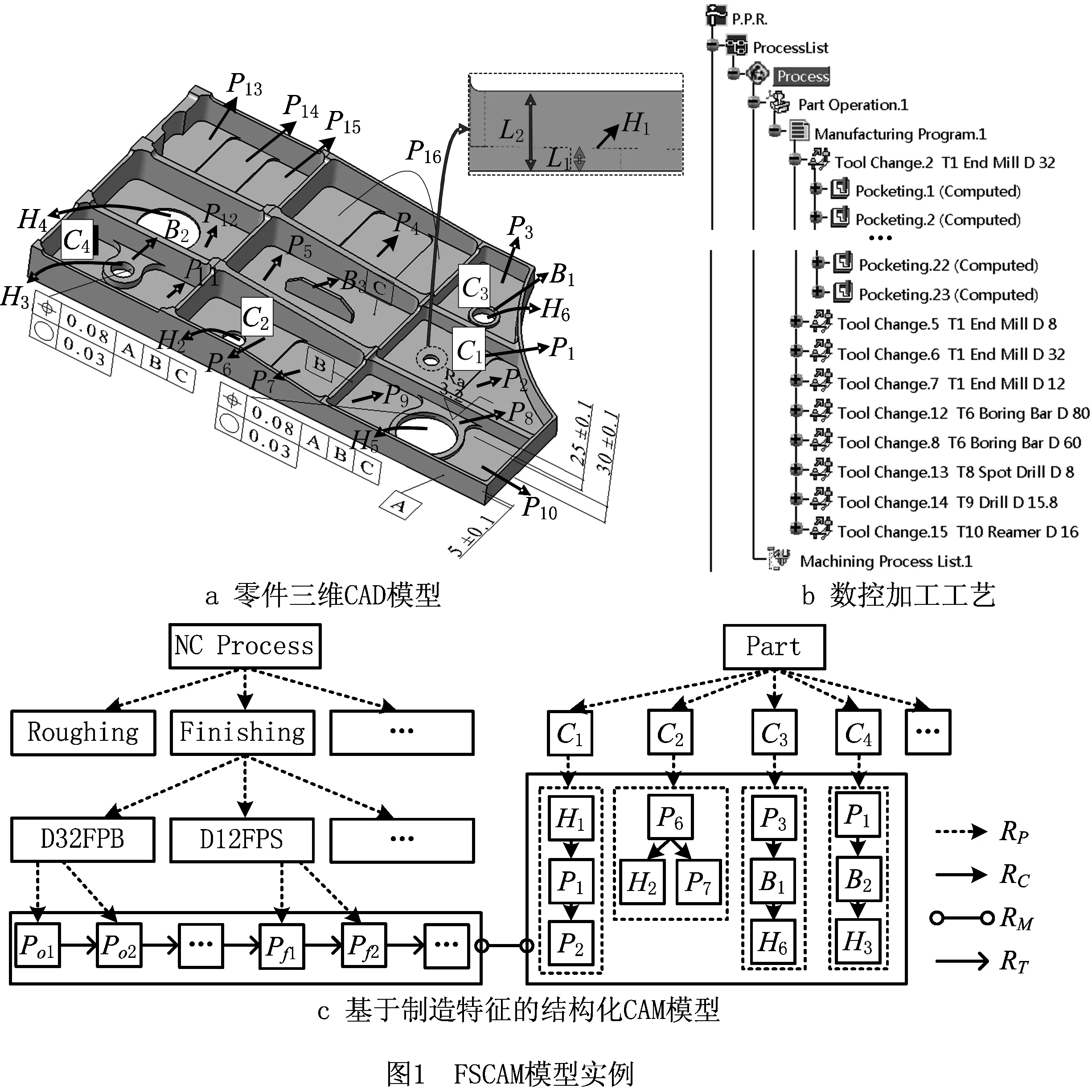
1.2 面向宏观工艺重用的三维CAD模型检索认知框架

为了清晰地描述本文方法在数控加工工艺设计过程中的作用，本文引入Belkin提出的一般认知与信息传递框架[10]，即用户为实现一定的目的，由此产生特定的需求，进而由需求触发对信息源的处理—信息的组织和表达，以及将信息向用户传递以满足用户需求。

根据一般认知与信息传递框架，本文提出面向宏观工艺重用的三维CAD模型检索认知框架，如图2所示。在该框架中，工艺设计人员的目的是高质高效地完成复杂零件的数控加工工艺设计。对于复杂零件，设计人员往往首先回忆是否有相似的零件，然后查找其相关的工艺信息，并直接重用或修改重用来完成数控加工工艺设计。在这个过程中，设计人员往往会陷入困境，例如查找相似零件困难，查找关联数控加工工艺困难，加工参数设置交互操作多。目前工艺数据的大量积累也加大了这些问题的难度，这进一步促使对能够自动高效查找数控加工工艺数据的三维CAD模型检索的技术产生需求。该需求触发了对工艺数据实例的处理，即零件模型及关联的数控加工工艺需要合理地组织与表示。在此基础上，对查询零件与工艺实例进行整体相似性评估，实现相似零件的快速查找与可重用宏观工艺的推送，最终满足工艺设计人员的需求，将设计人员从困境中解救出来。

由图2可知，该框架主要包括关联概率模型学习和整体相似性评价两个阶段。具体地：

(1)关联概率模型学习 针对工艺数据实例，实现其以工艺骨架为核心的结构化表征，主要包括FSCAM模型构建和基于工艺骨架的工艺知识模型(Process Skeleton-based Process Knowledge Model, PSBPKM)构建。并在此基础上，根据零件几何拓扑、精度要求对宏观工艺的影响特点，计算各工艺要素之间的关联概率分布，实现关联概率模型学习。该学习过程在离线阶段完成，不占用检索时间。

(2)整体相似性评价 根据学习到的关联概率模型，采用概率统计方法构建查询零件的制造特征与工艺数据的宏观工艺之间的关联映射关系，进一步计算基于该宏观工艺的零件整体相似度，并依据相似度将可重用宏观工艺推送给工艺设计人员。该评价过程为在线阶段完成，即检索过程。

2 关联概率模型学习

2.1 基于工艺骨架的工艺知识模型构建

为了学习出工艺数据中工艺要素间的关联概率，本文首先引入基于工艺骨架的工艺知识模型，对工艺实例进行聚合并结构化表示。

定义3基于工艺骨架的工艺知识模型(PSBPKM)。PSBPKM是以工艺骨架为核心，以FSCAM为实例，包含具有相似加工特性的制造特征簇FC、用于描述制造需求的工艺要素PP，以及与该组实例工艺要素相对应的概率分布P，可以表示为：

KM:=[W]PS∪(FC)∪

其中W为工艺骨架边的权重，表示该组工艺实例中工序间在同一零件中采用的次数，由实例统计获得。

给定一组来自CAM系统的工艺数据实例，包括CAD模型和CAM模型。在对工艺实例进行结构化表示后，根据工艺实例间的相似程度，通过宏观工艺层面的聚类，可以提取工艺骨架并将工艺实例向工艺骨架聚合，从而获得基于工艺骨架的工艺知识模型。具体地，该方法主要步骤如下：

输入工艺实例集V={PIi,1≤i≤n}；

输出基于工艺骨架的工艺知识模型集PSBPKMS={KMj,1≤j≤m}。

步骤1针对CAD模型，通过特征识别获得需要加工制造的特征F，并对特征间的耦合关系RC进行提取，具体提取过程参考文献[11]。

步骤2针对CAM模型，应用CAM系统的接口函数遍历其关联的数控工艺树并解析获取加工操作Op，并通过计算制造特征的加工面与加工操作刀位点的距离约束关系，构建制造特征与加工操作之间的关联映射关系RM，具体构建过程参考文献[12]。

步骤3根据加工操作的时序关系RT，通过相同工步意图加工操作的聚类，提取零件工步WS。进一步通过相同加工阶段零件工步的聚类，提取零件工序WP，获得零件的宏观工艺。

步骤4重复步骤1～步骤3，构建基于特征的结构化CAM模型FSCAM。

步骤5采用文献[13]中面向图的凝聚层次聚类算法(G-AHC)对FSCAM进行聚类，获得l个工艺实例簇PCC={PCk,1≤k≤l}。

步骤6遍历PCk中的工序语义，对其进行统计编码，并将工艺实例依据编码构建工艺优先图PPGki；

步骤7根据步骤5聚类过程中的匹配结果，将每类工艺实例中的工艺优先图PPGki进行融合，获得融合工艺优先图PPGk，并对节点对之间的协作次数统计作为边的权重。

步骤8重复步骤6～步骤7，输出基于工艺骨架的工艺知识模型集KMS。

图3以薄壁零件为例，构建该类零件基于工艺骨架的工艺知识模型。可以看出该类零件的工艺骨架为：D16粗铣型腔→D16精铣型腔底面→D8半精铣型腔轮廓→D8精铣型腔轮廓，由零件分析可知，该类零件工艺实例中都存在薄壁结构。由于F11的最小宽度为11 mm，需要增加工序(D8粗铣型腔)进行二次开粗。另外，由于工艺实例3中特征F31的转角较小，只有5 mm，在精加工前需要增加工序对转角进行加工。

2.2 工艺要素的表示方法

工艺要素的值涉及较多的数据类型(包括浮点型、区间型、字符型等)，在对工艺实例进行统计分析前需要对其量化表示，以获得统一、便于计算的数据格式。从数控加工工艺分析角度，为了生成零件的宏观工艺过程，设计人员需要分析或计算零件的整体拓扑、关键制造特征以及精度要求。因此，本文对于零件实例及其关联的宏观工艺，可采用特征属性、空间分布、工艺属性以及时序关系等向量来描述。

(1)特征属性Af

特征属性描述了零件的基本组成单元，并体现制造特征的关键特性，包括零件材料、制造特征类型、精度要求等。

1)材料/特征类型。

材料/特征类型从宏观角度描述了零件制造过程中需要满足的必要条件，对零件总体工艺方案制定、刀具选择等具有基础作用和影响。

2)几何尺寸。

为了有效表示制造特征的几何尺寸，本文采用制造特征的最小包围盒来表征，L、W、H分别表示最小包围盒的长、宽、高。

3)几何开敞性。

刀具几何的选择与特征的几何开敞性紧密相关。另外，几何开敞性计算与特征的类型相关，例如型腔采用理论刀具直径范围[D1，D2]，孔则计算径深比。其中，理论刀具直径范围采用中轴转换法[14]进行计算。

如图4所示为一个型腔特征的中轴变换实例。如图所示，特征F的极限刀具直径为Dmax(T)=25.109 mm，Dmin(T)=7.149 mm。采用直径D14和D6的刀具时所获得的有效切削区域，其可连续加工区域数量分别为3和7，对应的有效切削弧长为73.326 mm和78.023 mm。

4)公差/粗糙度。

公差/表面粗糙度直接影响制造特征的加工方法。对于几何拓扑相似、公差/粗糙度差异较大的零件，其对应的宏观工艺过程仍非常不同。因此，精度类制造语义在数控加工工艺分析中占有重要的地位，本文中加工精度包括最大/最小公差ITmax/ITmin，最大/最小表面粗糙度Ramax/Ramin以及形状公差Tf。

(2)空间分布As

空间分布信息描述了制造特征间的相对位置与关系，表征着零件的整体拓扑情况，其对于零件加工过程中所需的工位、加工方法有着重要的影响。本文对于制造特征Fi与Fj之间的空间分布信息采用8维向量Ds(Fi,Fj)表示：

Ds(Fi,Fj)=[Fi·zmin-Fj·zmin,

Fi·zmin-Fj·zmax,

Fi·zmax-Fj·zmin,v4,Dist(Fi-Fj),v6,v7,v8],

v4=Dist(Fi·center-Fj·center),

v6=Area(Fi·box∩Fj·box)/Area(Fi·box),

v7=Area(Fi·box∩Fj·box)/Area(Fj·box),

v8=ni,nj。

其中：Fi·box是以刀轴方向为基准的特征Fi的最小包围，Fi·center则为特征Fi的几何中心，Dist表示特征几何中心点的距离。其中：1～3维表示特征间在刀轴方向的位置关系，4～5维表示特征间在水平方向(垂直于刀轴方向)的位置关系，6～7维表示特征间的相交关系，8维则是特征间的相对角度，定义为特征刀轴方向的夹角。

另外，位置公差反映的是在零件设计要求方面制造特征间的工艺约束。因此，在几何与拓扑表示空间分布关系的基础上，本文将位置公差Tp作为空间分布关系的补充，可表示为Tp={type1,value1,…,typen,valuen}，其中，type表示位置公差类型，例如平行度，位置度；value表示公差值。

(3)工艺属性Ap

工艺属性主要是宏观层面的工艺参数，不涉及具体的加工参数(如主轴转速、进给率)，主要包括加工工步序列WS={WS1,WS2,…,WSn}以及相对应的加工刀具序列T={T1,T2,…,Tn}和加工余量参数序列δ={δa1,δr1,δa2,δr2,…,δan,δrn}。其中，加工刀具主要由类型TT，刀具长度LT，刀具直径D，刀具圆角半径r等参数描述。

(4)时序关系At

除了基本的工艺属性，加工工步在数控加工工艺方案中的位置也是决定宏观工艺的重要因素。因此，本文采用工步与初始和终止工步的最短路径作为当前工步的位置。

综上所述，本文设计了一个能够描述不同类型工艺要素的工艺实例量化表示方法，该表示方法对零件实例及其关联宏观工艺进行向量化表示，包括特征属性、空间分布、工艺属性以及时序关系。表1给出了本文各工艺要素的具体表示方法。

表1 工艺要素的表示方法

2.3 工艺要素的分布计算

通过PSBPKM对工艺数据进行结构化表示后，接下来在工艺骨架节点下计算各工艺要素的概率分布。根据工艺要素对宏观工艺的影响特点，可将工艺要素的概率分布计算主要分成3部分：工艺属性、特征属性、空间分布关系。下面对它们进行详细说明：

(1)工艺属性关联概率分布计算

对于工艺属性，工步及工步间时序关系构成了一类零件的宏观工艺过程。工序语义及其属性的频度能够有效描述该工序在一类零件加工过程中的重要性或参与度。工步序列的频度则能够有效反映零件数控加工工艺方案中的宏观工艺约束，例如，特征F1与特征F2之间形成薄壁，在零件的数控加工工艺方案中，通常工步精加工型腔底面之后安排工步精加工型腔侧壁。因此，本文对工艺数据实例中的工步语义及工步序列直接进行统计分析，从而获得工艺属性方面的关联概率，可以表示为：

(1)

式中：M为工艺实例中工序序列总数量；oi表示第i个工序序列是否是指定工序序列，是则oi=1，反之，oi=0。

(2)特征属性关联概率分布计算

根据制造特征的定义可知，材料、几何、精度要求等制造信息能够用来表征制造特征。对于离散值，与工艺属性关联概率计算类似，可以直接采用频率计算获得。对于连续值，假定特征所有制造信息独立且服从高斯分布，特征属性与加工工艺的关联概率则来自工艺数据实例的各属性的统计，可以表示为：

(2)

式中:μ与σ分别表示特征属性高斯分布G的均值和方差，Dg是特征属性向量。其中，需要注意的是统计计算都是在相同工序/工步下进行的。

图5所示为特征属性关联概率计算示例。在同工艺骨架的零件族中，采用工步D12粗铣型腔(δr=1 mm,δa=1 mm)进行加工的制造特征具有不同的尺寸(如24.5 mm,20 mm,14 mm等)和精度要求，以最小宽度Wmin作为示例。统计这些制造特征实例，采用高斯分布进行拟合，可以获得该零件族中特征最小宽度与工步D12粗铣型腔的关联概率服从均值μ=18.23，方差σ2=0.77的高斯分布。由此可以根据新实例的最小宽度值计算其关联该工步的概率值，从而判断新实例是否采用该工步，其余参数的分布计算相同。

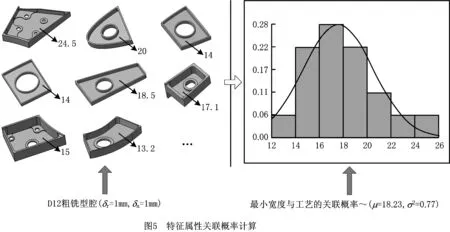
(3)空间分布关系关联概率分布计算

空间分布关系直接反映工艺约束，对于宏观工艺过程的制定有很大影响。在2.2节，已通过8维向量Ds表征制造特征间的相对位置关系，该向量描述了特征间的水平、垂直、相交以及刀轴方向关系。这些空间关系通常不是围绕单个均值分布，因而本文采用基于非参数技术的核密度估计[15]来表示空间分布关系与工艺的关联概率分布，可以表示为：

(3)

式中：W[x,y]表示从工艺实例中获得的工序x和y参与同一零件加工的工序集；k为该工序集中实例的数量；Dw则是工序集中第w个实例；K和h分别为核函数及带宽系数，两者的选取决定了核密度估计的精度。由于高斯函数具有更好的平滑性，本文采用高斯核函数。为了选择最佳的带宽h，需要进行交叉验证估计。在实验过程中，本文针对不同的空间分布关系分别预定义带宽值。

3 整体相似性评价

整体相似性评价主要是通过概率统计形式判断待制零件的制造特征与已有工艺数据的宏观工艺之间的关联映射关系，并根据关联映射关系计算待制零件与相匹配零件实例族之间的整体相似度。

3.1 特征与宏观工艺关联映射方法

经过关联概率模型学习后，可以获得特征与工艺关联的先验概率。对于给定的待制零件和宏观工艺，首先需要评价待制特征与工序/工步的关联性，在此基础上，建立特征工艺关联概率矩阵来实现宏观工艺驱动下的待制特征的定向聚合，从而实现待制特征与宏观工艺的关联映射。

根据工艺上下文(与当前工序相关的工艺要素)分析，特征与工序关联不仅与当前工序有关，还受已映射到的其他工序影响。当pg和ps计算方式确定以后，可通过考虑所有的已映射特征与工艺上下文来计算最终的待制特征与工序的关联概率，用P(F,WP)来表示，其定义为待制特征、已关联特征与工序关联的联合概率，假定关联概率间相互独立，其中，W为关联到同一工序的特征集，Wh为已关联到其他工序的特征集，即

(4)

P(CS|FS,PS)∝P(FS,PS|CS)P(CS)。

(5)

式中：P(CS)是制造特征与宏观工艺关联的先验概率分布，表示为：

(6)

P(FS,PS|CS)是条件概率，表示工艺实例中出现特征FS与工艺PS存在某特定关联关系(即聚合形式CS对应的关联关系)的概率，可由式(4)计算获得。

最后，聚合评价形式定义为式(5)的负对数：

(7)

式中E(x)=-log(p(CS)p(FS,PS|CS))。

聚合簇中的所有制造特征的关联概率值描述了该簇关联同一工艺的紧密性，而整个聚合形式的所有制造特征的E(CS)指标则反映了聚合结果的质量，E(CS)指标越大表示聚合质量越好。

下面给出宏观工艺驱动的制造特征定向聚合的主要步骤：

输入待制三维CAD模型M1、工艺数据集PCS的工艺骨架PS；

输出与宏观工艺对应的制造特征簇集合CS={Ck,1≤k≤l}。

步骤1从零件三维模型M1中提取制造特征Fi，记作FS={Fi,1≤i≤n}。

步骤2从工艺数据集PCS的工艺骨架PS中遍历加工工序/工步WPj，记作WPS={WPj}，1≤j≤m。

步骤3由式(4)计算制造特征与工序/工步的关联概率并构建特征工艺关联概率矩阵M：

步骤4应用模糊商空间聚类分析算法获取待制特征的分层递阶结构，根据不同的概率值p划分不同的聚类形式(如图6)。

步骤5计算每个聚合形式的E(CS)指标，选择质量最佳的聚合形式，最终输出制造特征簇集合CS。

根据特征与宏观工艺关联模型，通过待制零件与工艺骨架的概率计算并判断匹配程度，可获得查询零件P的宏观工艺方案。但是，对于P，该宏观工艺方案的可重用价值仍需要进一步计算零件整体相似度来判断。

3.2 整体相似度计算

整体相似度计算主要包括制造特征相似度计算、特征簇相似度计算和整体相似度计算。

(1)制造特征相似度计算

给定2个制造特征C(实例)和F(查询)，当C和F在同一加工阶段时，假如其有效加工区域越相似，则认为其加工工艺的可重用度也相应地越高。鉴于已有方法利用特征终态进行相似性比较存在评价粗放的问题，本文以宏观工艺驱动来计算特征相似度。每个加工阶段所考虑的加工侧重点各不相同，其有效加工区域表征形式也各不相同，本文依据不同加工阶段提取相应信息，如粗加工提取加工体积信息、精加工提取加工面积信息。同时，在相同加工阶段，有效加工区域MR的计算只与刀具、加工余量以及特征几何有关。因此，有效加工区域的计算主要包括如下两个步骤：①从特征几何中抽取特征轮廓线Ls以及岛屿轮廓线Lb；②依据刀具直径和加工余量计算Ls和Lb的偏置，并对原始轮廓线与偏置线进行布尔操作。本文采用文献[16]中的偏置算法。

图7所示为一个制造特征的多视角有效加工区域计算实例。MR11与MR21是制造特征F不同工序下的两个有效加工区域，MR11的有效切削面积为13 897 mm2，其有效切削深度为45 mm，MR21具有相同的有效切削面积，而有效切削深度只有1 mm。MR11与MR12是制造特征F相同工序下的两个有效加工区域，MR11是半径为8 mm的刀具所能加工的区域，MR12则是半径为4 mm的刀具所需加工的残留区域，其有效切削面积为193 mm2。

给定一把刀具d，它与加工工步WP相对应。假设φ1(d)与φ2(d)分别为d在WP下的有效切削区域，那么该加工工步下的加工特征相似度为

(8)

式中：φ(d)表示刀具的有效切削面积或体积；n1与n2分别为可连续加工区域数量，其与提刀次数密切相关。

(2)特征簇相似度计算

通过特征与宏观工艺关联映射后，查询零件P和关联工艺骨架的零件族PC之间的一个匹配M被成功找到，在此基础上，整体相似度可通过计算相匹配工步下查询特征簇FC(P)与实例特征簇FC(PC)的相似度获得。由于同一零件中相似特征的数量多少并不影响宏观工艺，本文采用特征簇中心实例来度量两个特征簇的相似度。假设特征簇FC包含L个实例{F1,F2,…,FL}，σij为Fi与Fj的相似度，FC的中心实例S(FC)定义如下：

(9)

这样，假定FC(P)和FC(PC)的中心实例分别为S1与S2，查询特征簇与实例特征簇之间的相似度可以表示为：

σ(FC(P),FC(PC))=σ(S1,S2)。

(10)

这里，σ(S1,S2)为特征间相似度，可由式(8)计算获得。其中，对于两个特征簇中实例均小于2的情况，采用平均值计算两个簇的相似度。

(3)整体相似度计算

整体相似度定义为相匹配零件与零件族在给定宏观工艺下的相似度η(P,PC)，可以首先根据特征与工艺的关联映射关系M来计算特征簇匹配对的相似度，进一步将这些特征簇匹配对的相似度进行加权求和获得

(11)

这里，特征簇匹配对的相似度σ(FC,M(FC))由式(10)计算获得。同时，权重可通过计算加工工步间的协作次数获得，即共同参与不同零件加工过程的次数。

4 实例验证

为了有效验证本文算法的有效性，作者以Microsoft Visual Studio 2008为集成开发工具，在CATIA V5 R21 CAA环境下实现了面向宏观工艺重用的三维CAD模型检索算法。

4.1 概率模型学习实例

图8给出了某模具制造企业的一组模板零件，零件材料为Cr12。该组模板零件的部分三维CAD模型如图8a所示(上部分布圈对应为D63粗铣型腔，中部右侧分布圈对应为D40粗铣型腔，中部左侧分布圈对应为D30粗铣型腔，下部右侧分布圈对应为D26粗铣型腔，下部左侧分布圈对应为D17粗铣型腔)。，其制造要求均相同。零件上存在较多不同尺寸的型腔特征，其几何尺寸的分布如图8b所示。在该零件族中，采用工步D17粗铣型腔进行加工的制造特征的最小宽度概率分布如图8c所示，其概率分布为服从均值μ=36.25，方差σ2=0.56的高斯分布。由图8可知，几何尺寸是影响该零件族宏观工艺的主要因素。从几何尺寸分布可以看出，工步的选取不仅与宽度有关，还与长度有关，这是因为这里的宽度可以代表最小可行刀具直径，而长度则可以代表加工区域的大小。对于相同的制造特征可能采用不同的工步，如图8b中相交部分，这时根据概率值选择最可能的工步，例如第3个模型中的宽37长55的型腔特征，可以采用工步D26粗铣型腔和工步D17粗铣型腔，由式(2)可得，其概率分别为0.041和0.671，因而该型腔特征倾向于选择工步D17粗铣型腔。

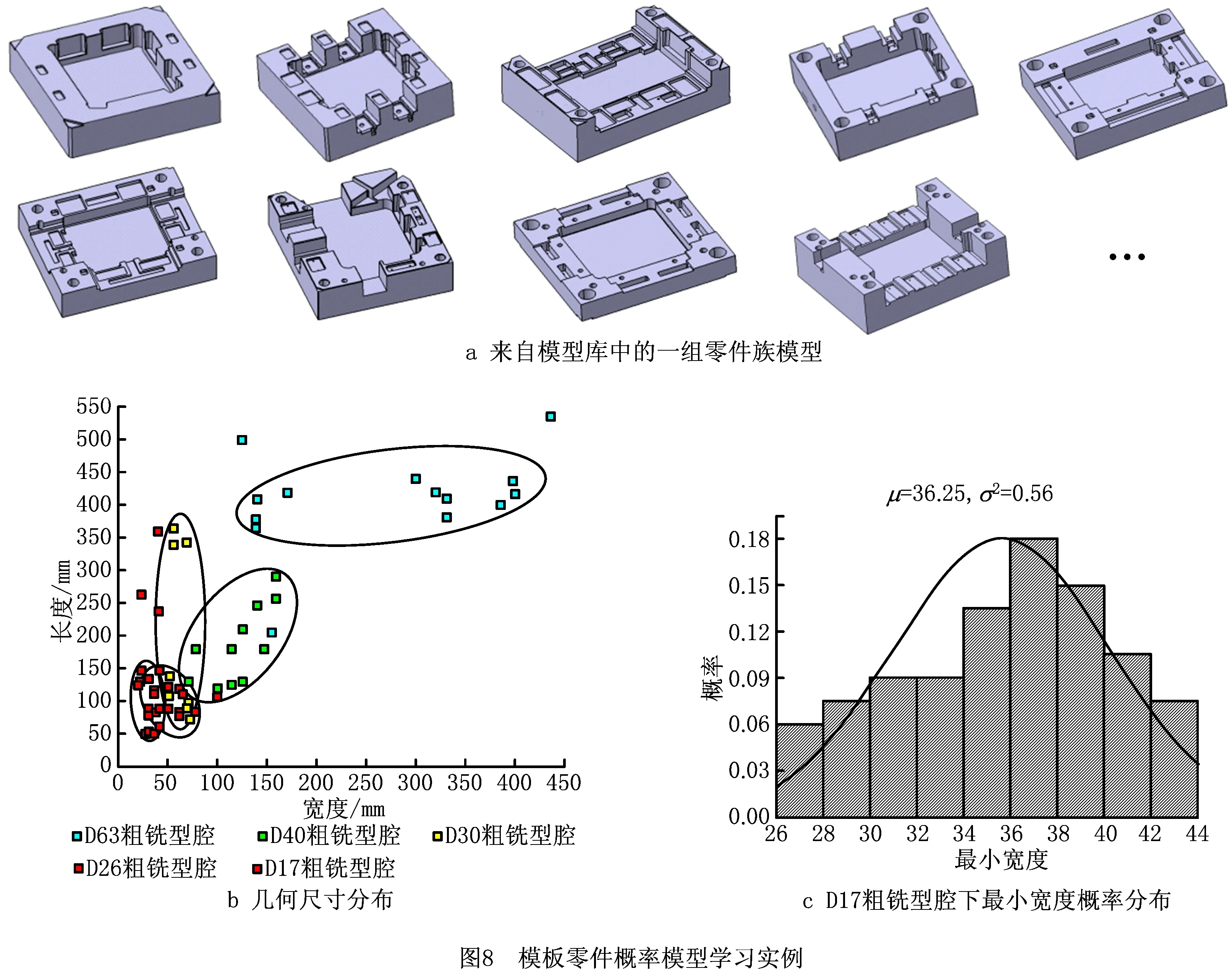
4.2 原型系统

图9给出了三维CAD模型检索的原型系统，包括结构化CAM模型构建模块与三维CAD模型检索模块。图9a所示为结构化CAM模型构建模块界面，其使用步骤如下：①制造特征自动识别与交互定义；②提取零件中的耦合关系并构建制造特征耦合簇；③从工艺文件中解析出数控工艺信息，提取工艺意图并构建宏观工艺。对于查询零件通过前两步骤来解析模型数据，而已制零件需要进一步解析数控工艺信息并提取宏观工艺。图9b所示为三维CAD模型检索模块界面，该模块的使用步骤包括：①在三维CAD模型检索模块中指定检索模式；②通过计算相似度进行检索。相似零件及其相似度会在检索结果列表中根据相似度由高到低显示出来。当某个检索结果被选中时，该零件模型在检索结果预览区中会被高亮显示。

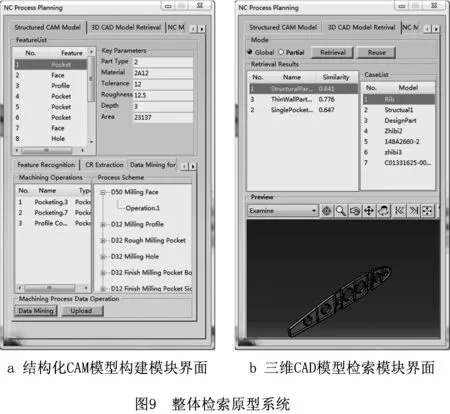
4.3 零件检索实例

表2给出了3个零件查询实例及其对应的检索结果(这里仅给出零件族中的3个零件模型)。在模型库中，为了提高检索效率，根据零件及其数控工艺进行了聚类划分，在检索过程中一类零件只进行一次匹配，能够与零件族关联的宏观工艺相匹配再进行相似性评价。在表2a中，检索出的零件族(1)中零件均为飞机结构件(薄壁结构)，具有相同的加工要求，并且关键制造特征相似(即F1，F2，F3，F4具有相似的几何开敞性)，这使得它们的工序、工步以及刀具非常相似，从而具有较高的相似度。相比于零件族(1)，零件族(2)则属于不同类零件，虽然结构简单，制造特征数量也较少，但反映了该类零件的加工方案，其中存在薄壁结构对宏观工艺制定具有决定性作用，这使得它们具有较高的相似度值。对于表2b中查询零件q2，该零件特点是存在较多不同尺寸的型腔特征，因而采用了较多的刀具，这使得工序数量增加。这里，零件的加工区域数量与值的不同并不会将它们从检索结果中排除出去，而只会影响相似度的大小。即零件整体拓扑结构、加工要求及关键制造特征等影响的是宏观工艺，而加工区域的大小影响的是加工效率。

表2c展示了双工位零件(代表多工位零件)的检索结果。很明显，单工位为多工位的特例。宏观工艺的影响主要来自与不同刀轴方向特征之间的空间分布关系。相对于查询零件q1，在相同刀轴方向上，查询零件q3的检索结果与其一致。

4.4 检索性能分析

图10给出了表2所示查询零件q1与q2检索结果的查全查准率图(Precision-Recall，PR)，该测试是在配有Intel Core i3 CPU 3.40 GHz和4 GB内存的PC机上运行的。实验中首先通过本文方法对测试模型库进行聚类划分，该模型库中的500个模型被聚类划分为46个零件族，然后分别对2个查询零件进行检索测试。由检索结果可知，各查询零件均能够较准确完整地检索出相似零件族。因此，其查准率均为1.0(在图中，其对应的查全查准率曲线相互重合)。其中，“Average”为整个模型库的查全查准率曲线。从图可以看出，当查全率小于0.6时，平均查全查准率曲线接近于1.0这条水平线，意味着随着检索到的相关零件数量的增加，零件检索的精度能够维持在一个较高的水准。此外，当查全率为1时，查准率达到了0.82。因此，本文的三维模型检索算法具有较好的检索性能。另外，以总用时作为评价指标，在所有的测试模型中，对这2个查询零件做检索效率方面的测试。查询零件q1，q2总用时分别为124.8 ms和110.6 ms，可以看出，查询零件所包含的特征的形状和拓扑结构越复杂，所需要的查询时间也越长。因此，本文的三维模型检索算法也具有较高的运行效率。

表2 整体检索实例

5 结束语

本文建立了以工艺骨架为核心的工艺知识模型，实现了对工艺数据实例基于宏观工艺的结构化表征，以及三维几何与数控加工工艺之间的深层次关联。引入概率统计方法，在工艺数据实例不断积累与丰富的背景下，将数据驱动思想融入查询零件制造特征与已制零件宏观工艺的关联映射关系构建中，以保证检索结果的可重用性以及检索方法的柔性。以宏观工艺为引导，工艺意图为驱动，计算查询零件与工艺数据实例之间的整体相似度，实现了从数控加工工艺角度对整体相似度的精准评价。

下一步研究工作包括：① 根据检索结果研究其关联工艺的重用实现方法，以提高零件数控工艺设计的智能化水平；②将本文方法扩展到其他知识重用领域，如曲面工艺设计、产品概念设计、装配规划等，以提高检索结果的可重用性与完整性。