木板抓取冗余机械臂逆运动学求解

徐呈艺，刘 英，贾民平，肖 轶,曹 健

(1.南京林业大学 机械电子工程学院，江苏 南京 210037；2.东南大学 机械工程学院，江苏 南京 211189；3.南通职业大学 机械工程学院，江苏 南通 226007)

0 引言

机械臂逆运动学是路径规划和伺服控制的基础。冗余自由度机械臂同一末端位姿会对应无数组运动学逆解[1]，具有较好的灵活性和避障能力[2-4]，可以更好地应用于工业、农业和服务业。但逆运动学求解比较困难[5]，目前国内外对其进行了大量的研究，主要包括代数数值法如雅可比矩阵伪逆法[6-7]、二次规划反向算法[8]；迭代算法如神经网络算法[9-10]、粒子群算法[11-12]、加权最小范数法[13]等；退化自由度法[14-15]；解析法[16-17]。文献[6-8]的代数数值法普遍都存在精度不高的问题，且每次只返回一个解，无法确定全部解。文献[9-13]的迭代方法运算量大、求解速度慢，不能满足机器人实时伺服控制要求；文献[14-15]的退化自由度法降低了机械臂的灵活性，失去了冗余机械臂的主要优点；文献[16-17]解析法求解过程采用位姿分离法，但未实现冗余度解耦，求解不全面；文献[18]引入自运动建立前3个关节姿态单位向量，求解后再进行逆运动运算；文献[19]引入自运动结合机械臂方向角以及人臂特性进行求解关节变量，求解较复杂。目前，引入自运动的研究技术文献中在臂型参考面时对前3个关节姿态矩阵求解较复杂，奇异点分析较少。

本文以用于木板抓取的七自由度拟人机械臂为对象，充分考虑七自由度机械臂的几何构型与向量特性，在建立正运动学模型的基础上，对该类机械臂逆运动学求解引入臂型角，并采用机械臂自运动结合位姿分离方法，其中由机械臂关节末端位置向量求解前4个关节角，由关节末端矩阵求解后3个关节角，分析机械臂奇异点，并对多组逆解进行优选。通过控制机械臂沿给定轨迹运动，对比其他算法时效与成功率等，验证该算法的性能，最后应用于木板抓取实例，验证其实用效果。

1 冗余机械臂正运动学

机械臂正运动学是后续逆运动学求解的基础。仿人双臂七轴冗余机械臂外形如图1所示，左右两臂完全对称，关节都为转动副，以其左臂作为研究对象。采用D-H法[20-22]建立关节坐标系，如图2所示，其中(Xb,Zb)为机械臂基座坐标系，(X0,Z0)为机械臂参考坐标系，(Xi,Zi)为机械臂关节i(i=1～7)的坐标系，(Xt,Zt)为机械臂工具坐标系，有D-H参数如表1所示。表中：ai为沿着xi方向从zi到zi+1的距离；αi为绕着xi方向从zi到zi+1的角度；di为沿着zi方向从xi-1到xi的距离；θi为绕着zi方向从xi-1到xi的角度。

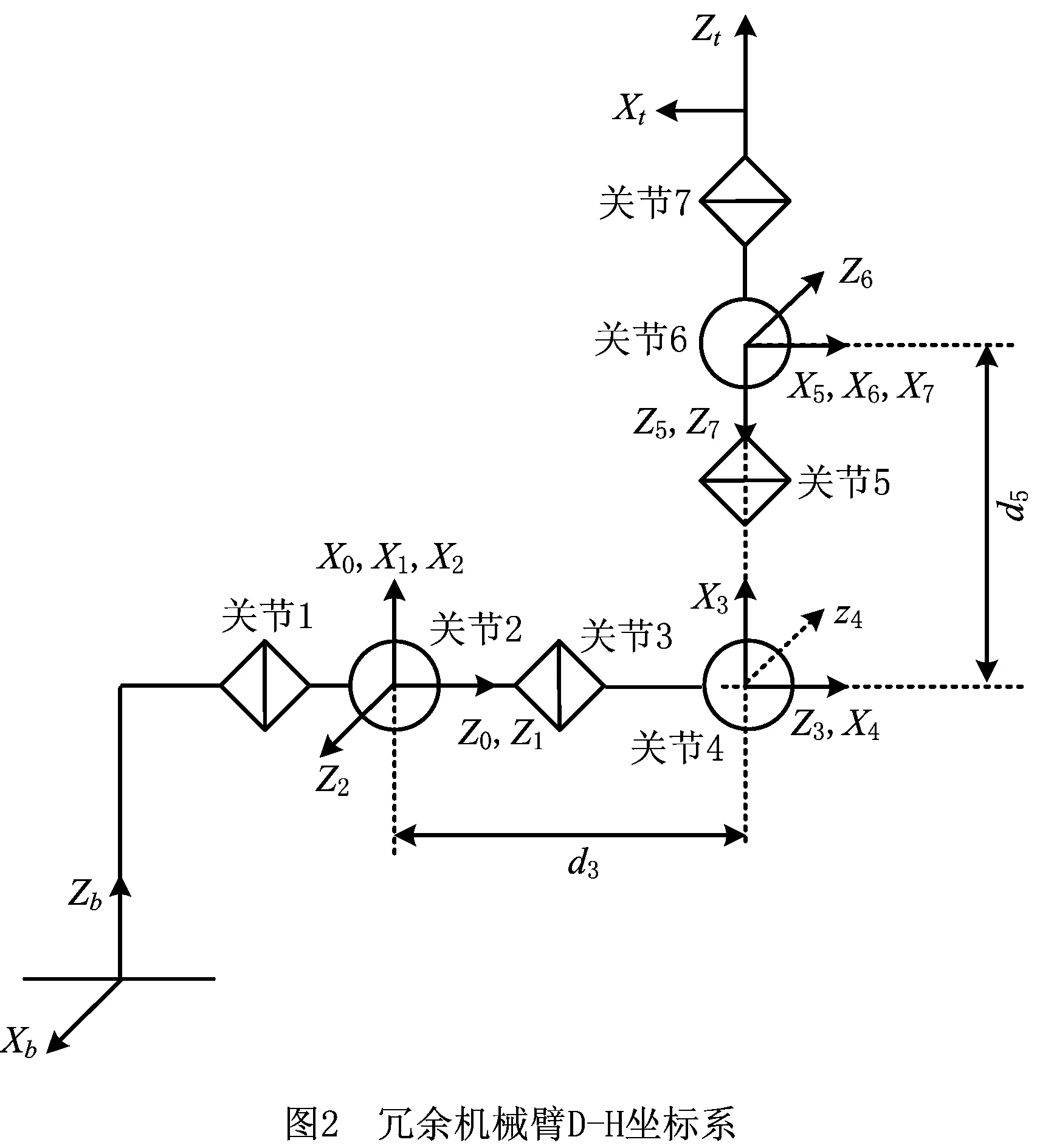
表1 冗余机械臂D-H参数

D-H参数可以用来描述相邻两个关节之间的变换关系，则相邻两个关节的变换矩阵为

Rot(z,θi)

(1)

(2)

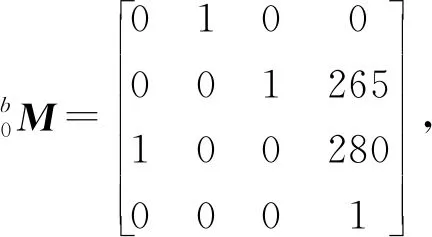
2 冗余机械臂逆运动学求解

2.1 θ4的求解

(3)

根据前述肘部自运动分析，关节4的角度θ4与臂型角无关，θ4直接由Δsew唯一确定，根据参考坐标系0建立的特点，可直接得

(4)

其中dse=d3，dew=d5，可解得

(5)

(6)

2.2 臂平面为参考平面时的求解

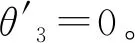
(7)

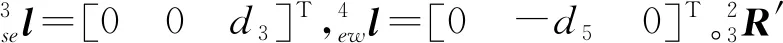
由正运动学模型结合参考平面相关向量可知机械臂末端位置向量有如下关系：

(8)

将式(7)代入上式展开运算则有：

(9)

对式(9)转换：

(10)

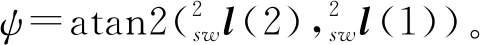
(11)

将(7)式代入式(8)展开运算有

(12)

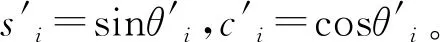
(13)

2.3 θ1、θ2和θ3的求解

当臂平面绕着虚拟轴sw旋转时，臂型角为φ，从参考臂型角到实际臂型角的自运动旋转变换根据Rodrigues公式可得：

(14)

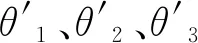
(15)

因此，可求得

(16)

又由D-H坐标变换可得

(17)

联立式(16)和式(17)可解得

(18)

2.4 θ5、θ6和θ7求解

由正运动学模型可知机械臂末端姿态矩阵有如下关系

(19)

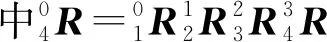
(20)

而根据D-H坐标变换又有

(21)

联立式(20)和式(21)可解得

(22)

2.5 机械臂奇异点分析

当θ4只有一个解时，即式(5)与式(6)相等，此时θ4=π/2，关节3与关节5旋转轴线重合，自由度减少，故为奇异点，θ3与θ5无法求解，但它们的和可求。

当θ2=0时，式(18)的θ1与θ3无法求解，此时关节1和关节3旋转轴线重合，自由度减少，故为奇异点，θ1与θ3的和可求。

当θ6=0时，式(22)的θ5与θ7无法求解，此时关节5和关节7旋转轴线重合，自由度减少，故为奇异点，θ5与θ7的和可求。

3 逆解的优选

在给定机械臂关节末端位姿与臂型角的情况下，根据前面分析的逆解求解过程一般有8组解，如图4所示。而实际上，当机械臂达到目标位姿状态时，其各关节角度是确定的。8组解在不考虑限位情况下都可以满足要求，只是每组的相同关节会存在不同转角。为了保证机械臂在抓取木板时，各关节轨迹连续，不发生突变，就要各关节跨度尽量小，即达到最短行程。

已知两个相邻的轨迹点A和B，机械臂末端在当前轨迹点A时时对应的机械臂的7个关节角度为qj，机械臂末端在轨迹点B时对应机械臂的逆解为qk，则需对在B点时的机械臂关节末端位姿进行逆运动学求解并选解，以达到两个时刻之间的行程最短，考虑到机械臂抓取木板运动过程中不同关节对末端位姿的影响，用加权重的构型空间距离作为评价函数，有

d=‖Qj-Qk‖2。

(23)

式中Q=(q1,q2,q3,2q4,2q5,3q6,3q7)。由于在对应轨迹B点时机械臂逆解Qk有多组，其中d值最小对应的一组机械臂逆解即为本文所选出的机械臂最优逆解。

4 实验

4.1 有效性测试

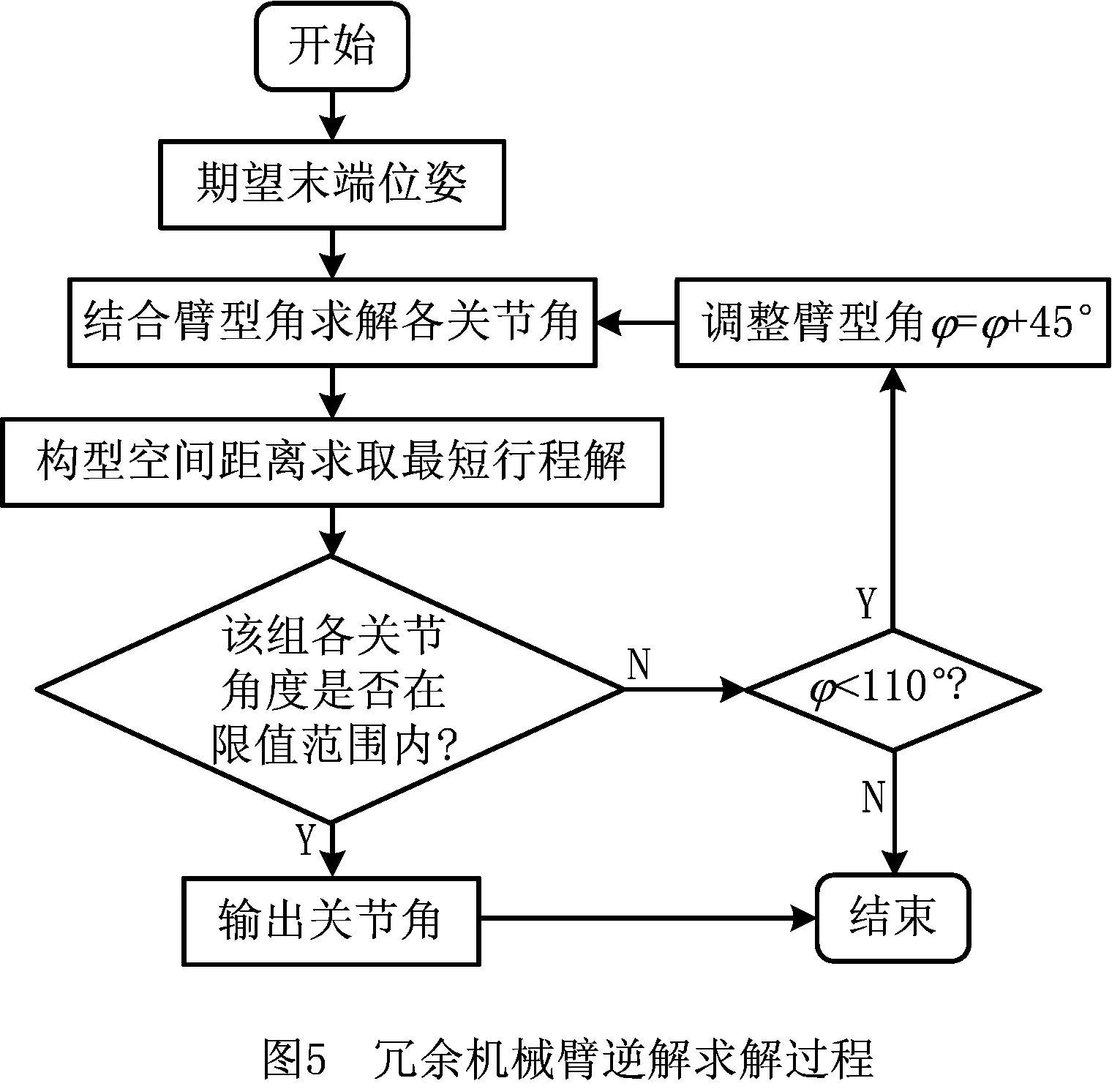
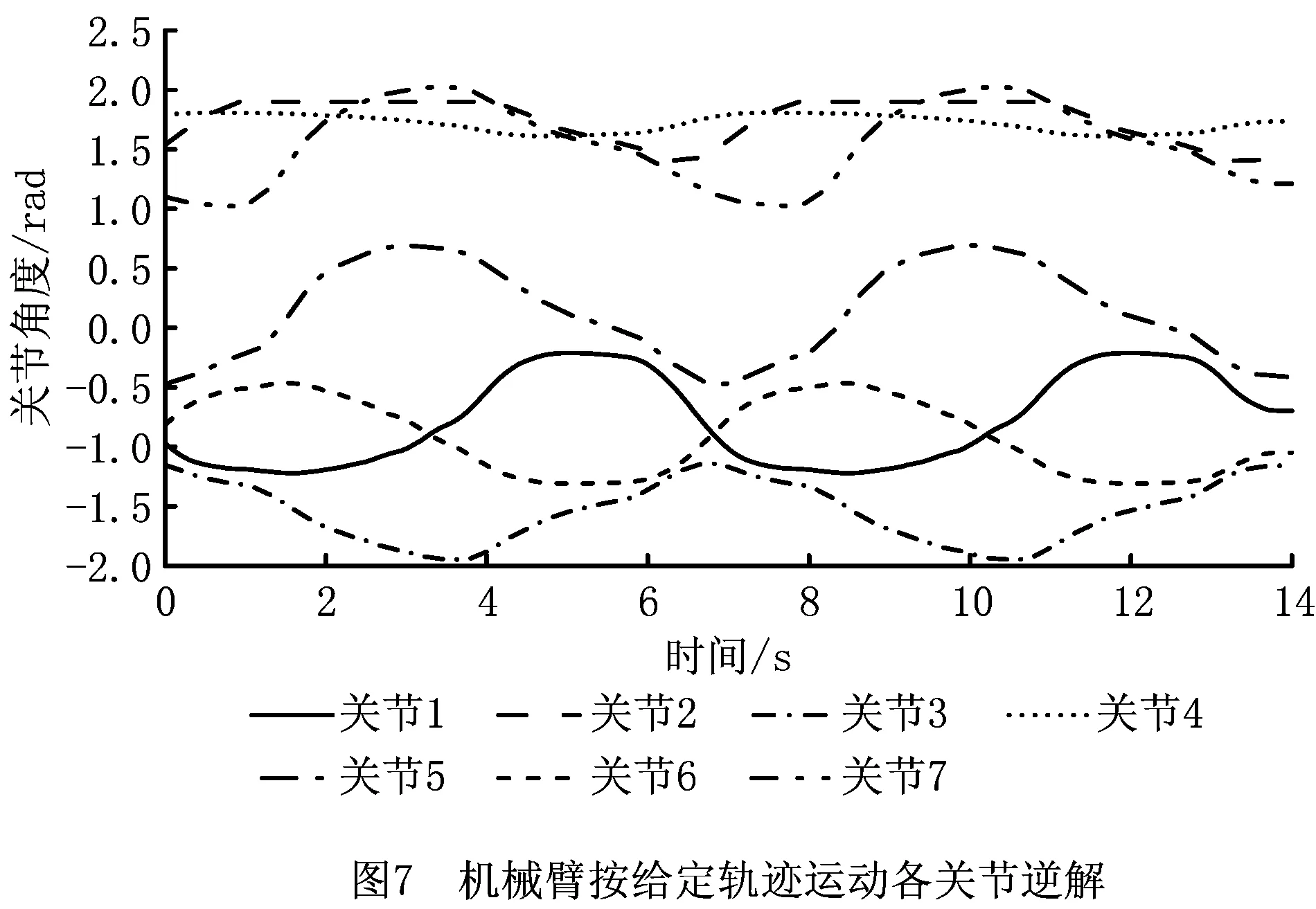
在机器人操作系统(Robot Operating System, ROS)中，建立了木板抓取机械臂运动学模型，冗余机械臂逆运动学具体求解过程如图5所示。首先由给定机械臂末端位姿和初始臂型角求解机械臂各关节角，臂型角初始值可设置为φ=0.785 rad，再根据构型空间最短距离对逆解优选，然后判断各关节角是否在最大范围内，满足要求则输出关节角，否则重新调整臂型角并进行逆解计算与优选。根据研究的逆运动学求解方法在臂型角固定的情况下控制机械臂，验证机械臂末端是否沿着给定的圆轨迹运动。当机械臂运动完后，可在3D可视化模块Riviz中显示其末端轨迹，如图6所示。机械臂运动过程中各关节角度即逆解的变化如图7所示，整个运动过程动作平稳流畅。在给定轨迹上采样64个点，按照前述方法计算机械臂逆解并优选，通过优选的逆解得到机械臂关节末端位置，与给定轨迹上对应采样到的到轨迹点对比，如图8所示。给定轨迹点与逆解轨迹点匹配，即机械臂可以按照图5的方法找到沿着给定轨迹运动的关节逆解，同时轨迹点的平均位置误差为4.35E-10 mm，说明研究的逆解求解方法正确且精度较高。

4.2 算法性能验证

为进一步验证研究的逆解算法的正确性，同时校验算法的性能，使用常见的几种算法求解逆运动学：雅可比数值解(Jacob-inv)[7]、TRAC-IK求解器[8]、Orocos项目中的KDL求解器[17]，以及本文研究的解析解算法(I-analytical)进行对比。实验过程如下：

(1)随机生成一组关节角度q0。

(2)用该关节角度计算机械臂运动学正解M0。

(3)计算q0时刻的臂型角φ0。

(4)利用M0计算机械臂运动学逆解。若实验组为数值解方法，设置其算法最高迭代次数为120，如果120次迭代内找到解，则返回逆解q，无返回则求解失败；若实验组为解析解方法，设定算法中的臂型角为φ0，所有返回的逆解组为qlist。

(5)如表2，成功率记录机械臂逆运动学求解的成功概率；平均耗时记录从计算开始所耗费的时间；平均位置误差是首先利用得到的逆解结果计算运动学正解，再与M0进行对比，并记录位置误差；找到q0占比(即完备性)，判断找到的逆解里是否有初始的q0。

(6)所有实验进行1万次。实验结果如表2所示，本文算法相对其他算法平均耗时少100倍以上、成功率更高，达到100%、平均精度达到3.75E-10 mm，所求到的机械臂逆解实际只取决于计算过程中的计算机程序所取数值精度。另本文方法能找到机械臂末端某一位姿对应的所有逆解。

表2 不同方法实验结果对比

4.3 木板抓取应用试验

机械臂关节末端当前位姿与视觉传感器识别的目标木板位姿之间需要插值形成机械臂末端轨迹。设当前机械臂位姿T0=(R0,p0)，需在t时刻运动到目标位姿Tt=(Rt,pt)实现木板抓取，为了位姿过渡更自然协调，设置位置和姿态插值分别如式(24)和式(25)所示：

(24)

(25)

插值后得到一系列位姿轨迹点，在相邻的轨迹点之间采用前述的逆解优选方法，根据机械臂与木板的实际位置，输出关节角控制机械臂运动实现木板抓取。在ROS系统中设置不同的目标木板位姿，进行1 000次实验，抓取木板均能成功，成功率为95.6%，其过程如图9所示，机械臂运行自动、快速、协调和平稳，达到要求。

5 结束语

本文充分考虑了用于木板抓取的七自由度机械臂几何构型与肘部自运动特性，采用D-H法建立了有利于逆运动学求解的关节坐标系和相应的正运动学数学模型。引入臂型角并将机械臂自运动结合位姿分离法对机械臂逆运动学进行求解。由机械臂关节末端位置向量求得第4个关节角和前3个关节角的参数化解，由关节末端姿态矩阵结合已求得的关节角得到后3个关节角，同时进行奇异点分析，并通过加权重的构型空间距离作为评价函数对逆解优选。该求解过程具有直观简便等特点。

通过控制机械臂沿给定轨迹运动并对比其他算法等试验，结果表明该方法成功率更高、运算量更小、速度更快，平均运行时间0.001 21 ms左右，实验结果精度更高，机械臂末端位置平均误差为3.75E-10 mm左右。应用该方法在不同目标位姿进行木板抓取试验，机械臂在抓取过程中运行平稳流畅，抓取目标成功率高，在冗余机械臂视觉伺服等实时控制中有较好的实用意义，如通过视觉识别待抓取目标位姿，通过本文算法实现机械臂末端高效的定位操作。