基于特征排序—神经网络算法的表面粗糙度预测

朱俊江，濮 玉，周柔刚

(1.浙江大学 能源工程学院，浙江 杭州 310058；2.中国计量大学 机电工程学院，浙江 杭州 310018；3.杭州电子科技大学 机械工程学院，浙江 杭州 310018)

0 引言

表面粗糙度指加工表面具有的较小间距和微小峰谷的不平度，是零件表面质量的重要参数。它由所采用的加工方法和其他因素共同形成，对机械产品的使用寿命和可靠性有重要影响。一些重要零件在高速、高压、高温等特殊环境下工作，表面层的任何缺陷不仅直接影响零件的工作性能，还可能引起应力集中、应力腐蚀等现象，加速零件的失效，如果不对表面加工质量进行检测，可能带来严重的安全隐患和事故。目前，实际生产中普遍采用“先加工，后检验”的方式检测零件的表面粗糙度。这种方式成本高、效率低，而且无法事先发现不合格产品，已经不能适应自动化、智能化生产的需要，因此开展粗糙度在线测量技术的研究已经刻不容缓。

从被测量的角度可以将表面粗糙度在线检测方法分为直接法和间接法两大类。其中直接法指的是利用图像[1]、激光等手段直接对表面微观形貌进行测量。直接法测量表面粗糙度的准确度较高，但实际生产中加工现场往往伴有切削液，切屑等影响，降低了直接法的测量效果，增大了其走向实际应用的难度。为了间接得到工件加工后的表面质量，许多研究聚焦在如何建立各式各样传感器信号与工件表面加工质量之间的关系。这些传感器信号包括振动信号[2]、声信号[3]，切削力[4-5]等。为准确获取工件表面加工的质量，一般需要两个步骤：①选择和布置传感器，搭建信号采集系统以获取信号；②对信号进行特征提取和预测。其中，如何选取合适的信号处理方法进行特征提取和预测制约了预测的准确性，已经成为近年来的研究热点。

针对间接法测量工件加工后的表面质量，国内外已经开展了大量研究。在特征提取方面，时域分析具有算法简单，运行速度快的优点，因此得到了广泛应用[6]。但时域分析在某些情况下准确性不高[4]。因此，奇异普分析[7-8]、主分量分析等[9]算法一一被应用到了信号的特征提取方面，另外一些频域、时频域方法，例如傅里叶变化[10]、功率谱密度[11]，小波包分解[2]等也得到了广泛应用。在预测方面，常用算法包括支持向量机[12]，神经网络算法[13]等。这些研究都对间接测量加工工件的表面粗糙度具有指导意义。但这些研究中的特征提取方法均由执行者根据自己丰富的工程实践经验得到，并没有对所选特征进行量化分析，而且忽略了特征提取对预测的直接影响，特征选择的目标是寻找最优特征子集，剔除不相关或冗余的特征，从而达到确保特征有效性、提高模型精确度、减少运行时间的目的。因此，为了优化特征的有效性，并将特征提取和预测环节联系起来，本文提出采用特征排序的方法配合交叉实验综合调整预测算法，以提高表面加工精度的预测。

1 方法描述

本文采用模式识别的方法，建立振动信号与表面粗糙度之间的关系，整个方法分为特征提取和预测两部分。传统上，特征提取方法均由执行者根据自己丰富的工程实践经验得到，且孤立了特征提取和预测两个环节，未考虑它们之间的关系。为了优选出特征提取方法，并设计出与特征提取方法匹配的分类器，本文基于相关系数的方法对所提的特征库中的特征进行了排序，并基于排序结果优化了神经网络结构。

1.1 基于小波包分解的特征提取

小波变换(Wavelet Transform, WT)是一种时—频域分析方法，它通过平移称为母小波的函数获得信号时间信息，通过缩放母小波函数的尺度获得信号的频率特性。信号的时间信息和频率特性通过信号与母小波函数内积得到的系数来表达，如式(1)所示：

W(a,b)=〈x(t),ψa,b(t)〉

(1)

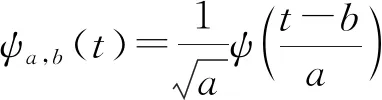
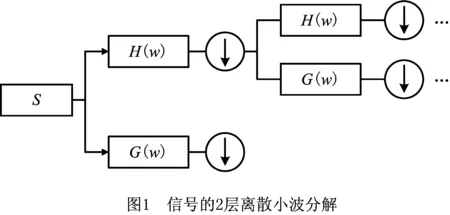
在图1中，H(w)和G(w)互为镜像滤波器，H(w)为低通滤波器。离散小波变化每次变换都只对低频部分进行分解，对信号的细节特征的描述能力不强，因此在对非平稳信号进行分析时，小波包分解往往取得更好的效果。小波包分解(Wavelet Package Transform, WPT)能同时对信号的低频与高频部分进行分解，提高了信号的时频分辨率。

采用如图2所示的小波包分解得到的DDD、DDA、DAD、DAA、ADD、ADA、AAD、AAA包含了信号在不同频段的信息，对分解得到的系数求取统计量，可作为预测粗糙度所用的特征。主要的统计量包括均值、标准差、峰峰值、偏度值、峭度值和能量熵，如表1所示。其中λi={DDD、DDA、DAD、DAA、ADD、ADA、AAD、AAA}表示进行统计时针对的分量；sj={Gx,Gy,Gz}分别表示x,y,z轴振动信号。

表1 选用的统计量特征

1.2 基于神经网络的预测算法

神经网络是一种具备自适应与自组织能力的学习型系统，具备非线性映射能力，其中BP神经网络具备自学能力强、推广和概括能力强等特点。典型的前馈神经网络一般包括一个输入层、一个输出层、一个或者多个隐藏层。对于浅层神经网络，由于增加隐含层个数并不能明显提高算法精度，三层神经网络得到了广泛应用。图3给出了三层神经网络的架构：输入层神经元个数与神经网络输入个数相同，当采用采用线性函数作为激活函数时，输入层的输出就是网络的输入；隐藏层包含若干个神经元，每个神经元的输入由上一层输出的加权和以及偏移组成，隐藏层的输出由隐藏层输入经激活函数作用而得到。因此，假设三层神经网络的输入x∈Rn，隐含层的输出h(x)∈Rm可以表示为式(2)：

h(x)=f(W1x+b1)。

(2)

(3)

式中：b2∈RL为偏移向量，W2∈Rl×m是权重矩阵，其中l为输出层神经元数，其与预测项目类别的数量有关，本文中仅对表面粗糙度的Ra值作预测，因此设定l=1。g(z)为非线性的激活函数。当给定一系列样本数据X={xi}及标签Y={yi}时，用神经网络最小化式(4)来确定最优的网络参数θ={W1,W2,b1,b2}：

(4)

1.3 基于特征排序的预测算法优化

特征提取和预测两个环节是模式识别法的两个重要且相互依赖的环节，在进行特征提取时，提取到的特征作为预测算法的输入，因此，特征的数量和特征之间的相关性都严重影响算法效果[14]；而在采用神经网络及其他类似的监督学习算法进行预测分析或回归分析时，也需要设计出合适的网络结构与特征进行匹配。为此，本文在传统模式识别方法的基础上，引入了相关性分析。首先利用相关性分析对提取到的特征进行排序，然后根据排序结果，采用正交实验的方式优化设计出选取特征的个数以及神经网络算法的隐含层神经元个数，具体算法如下：

输入振动信号集合S;

输出最优网络NET。

将集合S随机划分为训练集Str和校正集Sv；

采用小波法对每个信号sk进行3层分解，得到信号8个不同的分量DDD、DDA、DAD、DAA、ADD、ADA、AAD、AAA；

采用表2中的参数，对8个不同的分量进行统计，得到48个特征值；

针对Str根据相关性准则对特征量进行排序[F1,F2,…,F48]；

For i=48:1

选取特征[F1,F2,…,Fi]作为输入；

For j=1:10

初始化隐含层神经元个数为j个；

End

其中，相关性准则实质是用相关系数定量评估单个参数与结果之间的相关程度。已知第i个特征xi和标签y时，相关系数被定义为式(5)：

(5)

2 实验

采用如图4所示的实验系统对本文所提方法进行了验证。

采用型号为Z540B的钻削加工中心光机对材料为6061铝合金，大小为12×12×24 mm的长方体铝块进行进行铣削。该机床主电机功率为5.5 KW，电主轴最高转速为24 000 r/min。系统使用的是BT30刀柄和直径10 mm的三刃立铣刀。在铣削之前铝块已经进行了粗加工。铣削过程中，对铝块、刀架、夹具的振动情况以及铣削过程的声音情况进行了监测。其中，振动信号采用北京东方振动和噪声研究所生产的INV3062T0 24位4通道振动采集仪，与美国Dytran 3263A2三轴振动加速度传感器配合获得，采样频率设置为10 240 Hz。铣削加工参数的设定如表2所示。

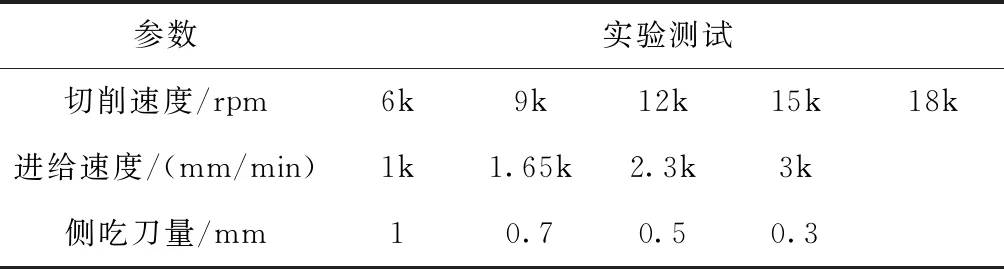
表2 铣削加工条件

采用SJ-210SJ-210粗糙度仪，以轮廓算术平均偏差Ra作为衡量指标，对加工后铝块的表面粗糙度进行了测量。测量时，将工件表面分为4个等距采样区域(D1，D2，D3，D4)，如图5所示。其中：D1和D4表示靠近卡盘端口的工件两侧区域，D2和D3表示工件的中心区域。

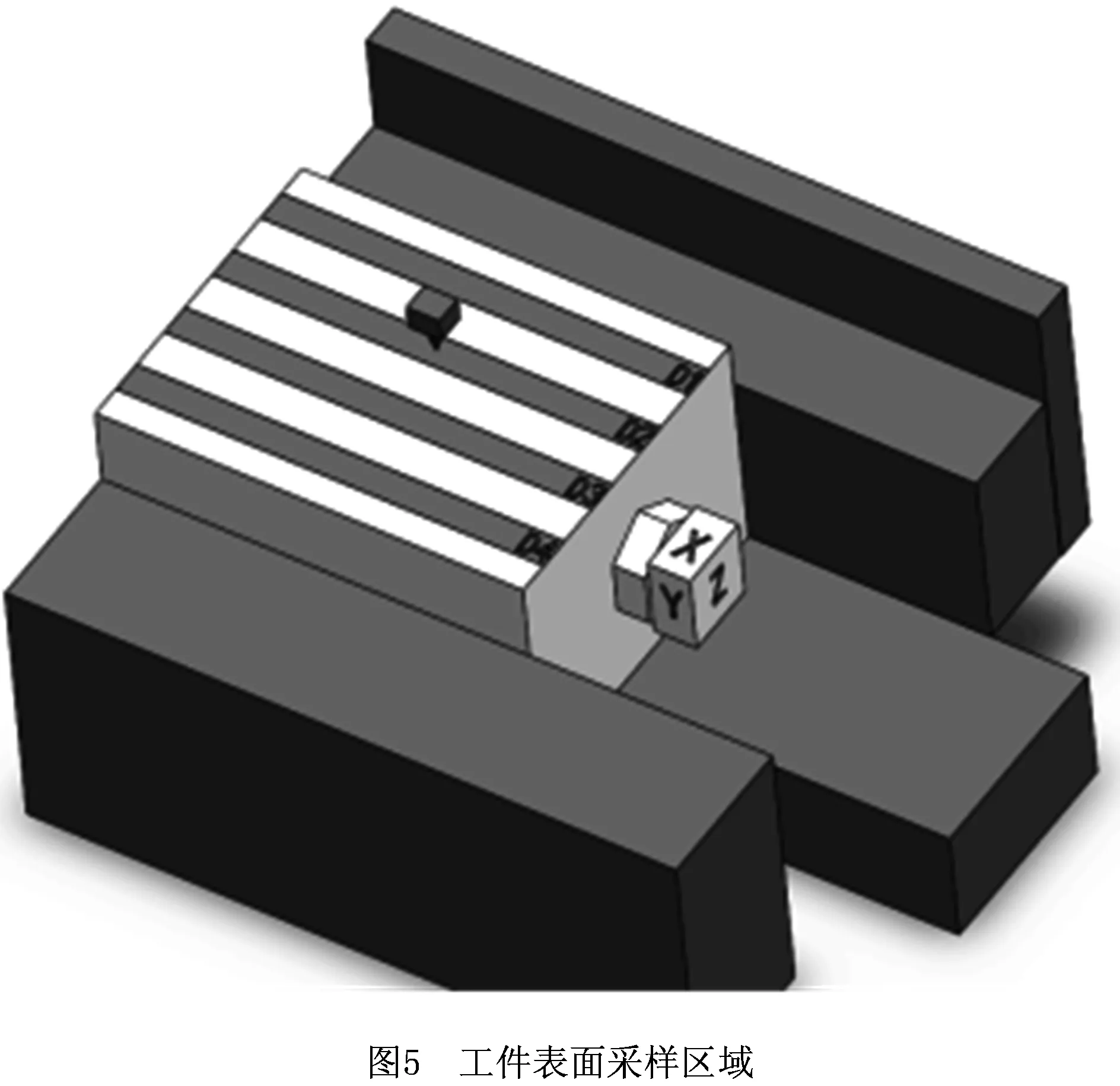
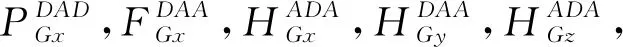
表3 表面粗糙度预测结果

文献[15]根据时域分析法处理振动信号并结合切削参数作为预测模型的输入，但由于振动信号的频率成分复杂，因此平均偏差大于其他方法。文献[2]和文献[4]均采用了小波包+统计量的方法对信号进行特征提取，并且统计量指标均为表1中给出的均值、均方差值等6个量。表4给出了使用文献中所提方法针对本文实验的数据得到的平均偏差，相比于文献中针对车削实验得到的数据，这些方法在处理本文中的铣削实验数据时，准确率均得到小幅度提升。从表4中可以看出，在针对本文中的铣削实验数据时，所提方法预测的表面粗糙度平均偏差为6.57%，比G-WPT低4.15%，相比于G-WPT对每个特定分解级别上获得的数据包都进行参数评估和表征，本文所提的方法根据相关性分析所得特征排序结果优化了特征个数，明显降低了计算成本，相比于文献[2]和文献[4]所用的多项式回归方法，本文所提基于特征排序—神经网络算法在处理粗糙度预测方面具有一定优势。

表4 研究方法结果对比

3 结束语

采用工件加工过程中的振动信号对加工后表面粗糙度进行预测，有利于实现工厂的自动化和智能化生产。本文首先采用小波包分解法对振动信号的特征进行了提取，然后利用神经网络对形成的表面粗糙度进行预测。为了设计出相互匹配的特征提取方法和预测方法，采用特征排序的手段优化了提取到特征的个数以及神经网络算法的参数。以6061铝合金铣削加工为例，对加工时的振动信号和加工后的表面粗糙度的轮廓算术平均偏差进行了测量，采用测量到的数据对所提方法进行了验证。实验结果证明：所提方法的预测偏差分布在0.005 7μm～0.066 7μm之间，平均偏差为6.57%，预测值与实际值比较接近，证明具有潜在的应用价值。本文在优化提取特征之前首先建立了一个由48个特征组成的特征库，然后利用特征排序的方法对特征进行筛选，因此，最终结果可能受限于特征库的组成。如何挖掘出更多的潜在有效的特征，或者设计出端到端的特征提取方法，还有待于进一步的研究。