基于遗传规划的泥石流多因子融合预测方法

翟淑花，冒 建，南 赟，刘欢欢，王云涛，王强强，熊春华，王艳梅

(北京市地质研究所，北京 100120)

0 引言

泥石流是山区多发频发突发的地质灾害之一，常给人民生命财产安全带来极大威胁，泥石流预警作为泥石流防治的有效手段，一直是众多学者研究的焦点问题。多年来，针对降水在泥石流暴发中的触发作用公开了大量研究成果及工程实践经验[1-14]。有学者采用线性拟合、Logistics回归等方法建立了前期有效雨量、小时雨强、过程雨量等降雨指标的泥石流灾害临界预警表达式；也有学者采用人工神经网络建立了泥石流非线性预警模型，但预测精度在很大程度上依赖于使用者的经验与水平，限制了模型推广和应用。大多数地区的泥石流预警模型中以降雨作为预警因子，而较少涉及泥石流流域形态、地质岩性等地质环境背景因素，造成泥石流预警多以区域预警为主，泥石流精细预警程度不高。因此，本文以泥石流孕灾因子、降雨指标为预警指标，以遗传规划为手段，建立以泥石流地质环境背景为基础的泥石流综合预测模型，提高预测模型的普适性和可靠性。

1 遗传规划模型的构建

在历史泥石流地质因子和降雨数据分析的基础上，采用遗传规划建立地质因子与关键降雨因子之间非线性函数关系，输出泥石流预测二叉树模型，实现不同地质环境背景下的泥石流预测(图1)。

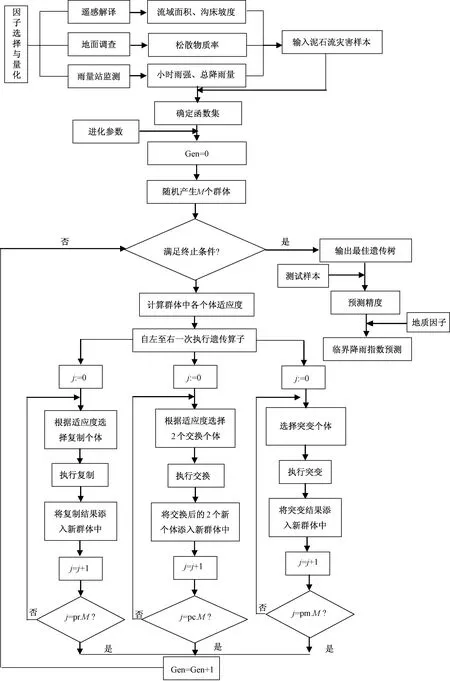
图1 基于遗传规划的泥石流多因子融合预测方法流程图Fig.1 Multi-factors fusion method of debris flow prediction model based on GP

1.1 泥石流暴发影响因子的选择与量化

充分搜集历史泥石流灾害事件，以遥感解译，历史地面调查为手段，获取历史泥石流地质环境背景因子，收集泥石流沟域内历史雨量站数据，建立以流域面积、松散物质比率、沟床平均坡度等地质因子为自变量，以小时雨强、当日雨量为因变量的历史泥石流样本库，并将样本库样本分为学习样本和测试样本。

1.2 遗传规划模型的建立

以学习样本为基础，根据泥石流影响因子的特征，确定函数集和终止符集，函数集F可以从运算符或函数符中选择F={+,×,/,sin,cos,log,exp}，终止符集可选择变量X，Y，Z或常数。设定遗传规划进化参数，初始群体产生方法、群体规模、交换概率、突变概率、选择方法、最大允许代次、最大突变深度、以及终止准则等。遗传规划程序开始寻优搜索，满足终止准则后，输出临界降雨因子与地质因子之间的非线性函数表达式，建立泥石流综合预测模型。

(3)模型的验证与应用

将测试样本带入建好的模型，得到预测的临界降雨指数，并与实际临界降雨指数作比较，计算模型的预测精度。整个方法的技术流程见图1。

2 模型应用

2.1 选择泥石流预测因子

泥石流的暴发具有随机性和不确定性，受地形地貌、地质条件以及人类工程活动等众多因素影响。泥石流暴发影响因子的选择对预测精度具有重要影响，若因子选择过多，会增加模型的负担，降低模型应用效果，若因子考虑偏少，则会降低模型预测精度。鉴于此，在充分借鉴国内外已有研究成果的基础上，选择流域面积、松散物质比率、沟床平均坡度为影响泥石流临界雨量的自变量，以最大小时雨强和总累计雨量的乘积为因变量，建立不同地质环境背景下的泥石流临界降雨指数预测模型，各因子具体含义如下：

(1)流域面积(X1)：以流域出口为基准点，基准点以上分水岭为界的流域面积。

(2)松散物质率(X2)：流域内松散物质面积与流域面积的比值，其大小与岩层理化性质、地质构造、地下水的多寡、边坡坡度、植被状况等因素有关。

(3)沟床平均坡度(X3)：沟床平均坡度=tan-1(高程差/主沟长度)，为达到单位的统一，采用平均坡度的正切值作为计算因子。

(4)降雨指数(RTI)：为最大小时雨强(R)×总降雨量(T)/1 000，其中最大小时雨强为降雨过程中的最大小时降雨量(R)，总累计雨量(T)为当日雨量与前期有效雨量之和，前期有效降雨量采用前5天有效降雨量。

2.2 建立历史泥石流样本库

参考文献[15]中所列历史泥石流数据，建立以流域面积、松散物质比率、沟床平均坡度为自变量，降雨指数为因变量的泥石流暴发综合因子样本库，具体明细见表1。

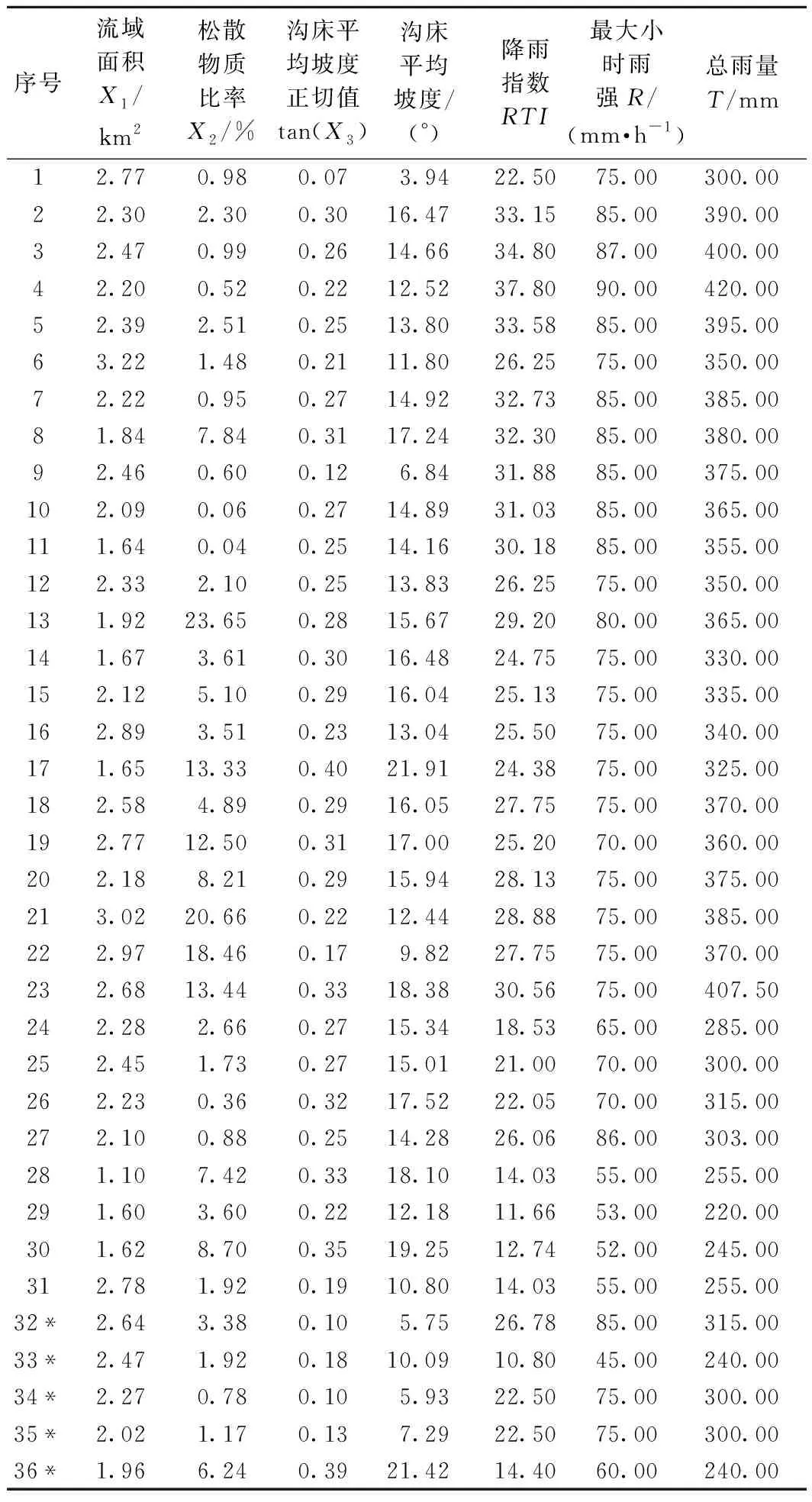
表1 泥石流暴发综合因子一览表Table 1 Comprehensive factors due to debris flow

2.3 建立遗传规划泥石流预测模型

以表1中前31项数据为训练样本，设定遗传规划模型参数如表2所示，经过遗传规划程序的反复学习和训练，当满足最大迭代次数51次且目标函数误差值最小时，获取泥石流暴发降雨指数与自变量X1、X2、X3的函数关系式(图2)，其中X1、X2、X3分别代表区域流域面积、松散物质比率以及沟床平均坡度的正切值。

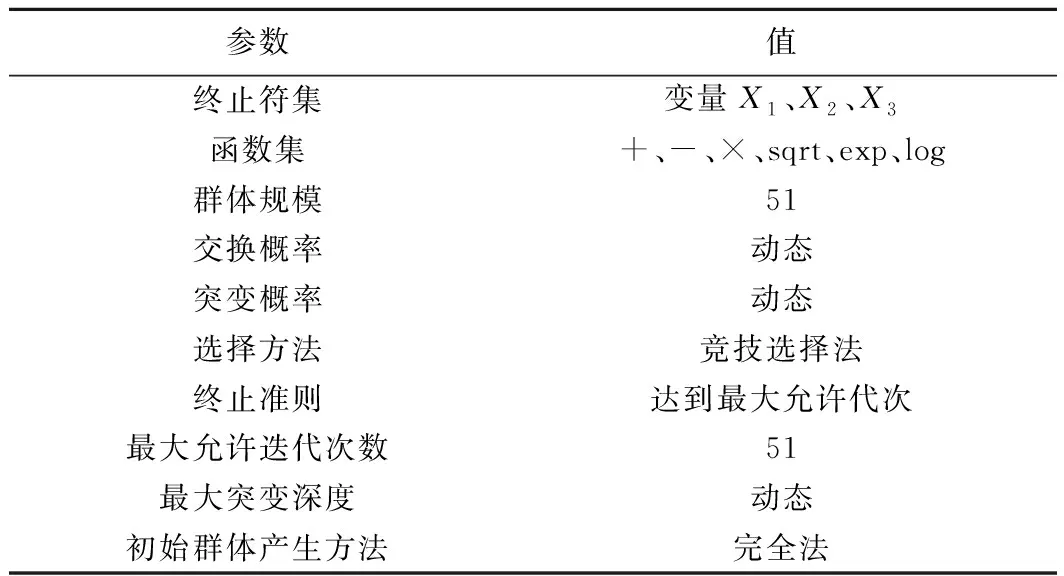
表2 遗传规划的基本参数一览表Table 2 Basic parameters of genetic programming

2.4 泥石流预测模型验证

将表1中带*的测试样本带入泥石流暴发降雨指数预测模型，得到各测试样本对应的降雨指数RTI预测值(表3)，并计算各预测值与实测值的相对误差((预测值-实测值)/实测值)，当预测值大于实测值时相对误差为正值，反之则为负值，计算结果显示，5个测试样本相对误差均在8%之内，满足模型预测精度要求。

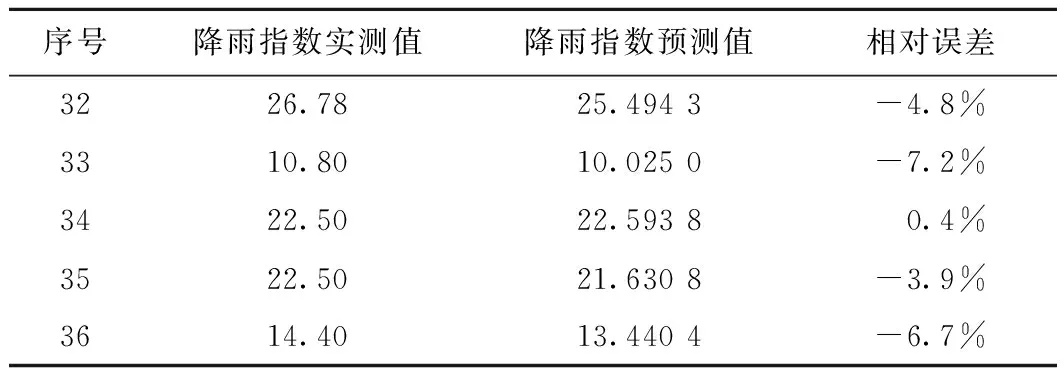
表3 基于遗传规划的泥石流临界降雨指数预测误差一览表Table 3 Model prediction error

3 结论

(1)泥石流是一种多发的地质灾害，常对人民生命财产安全带来极大的威胁，其暴发不仅与降雨有关，还与众多地质环境因子相关。本文以流域面积、松散物质比率、沟床平均坡度为地质因子，以最大小时雨强和总降雨量的乘积作为降雨指数，在获取的泥石流地质因子和降雨因子综合样本库的基础上，采用遗传规划法建立了基于地质因子的泥石流临界降雨指数预测模型，克服以往仅以单雨量为泥石流预测指标的弊端。

(2)与传统参数识别方法相比，基于遗传规划的泥石流多因子融合预测方法不需要进行模型的事先假定，只需经过选择、复制、交换和突变等遗传操作、逐步迭代而逼近最优解，并采用二叉树的形式输出泥石流地质因子与降雨因子的因素之间确定的非线性表达式。

(3)基于二叉树的遗传规划方法，仿照生物界进化过程，采用复杂多变的树状结构表达多变量之间线性或非线性数学关系，适用于处理大型、复杂的非线性问题，为解决类似非线性问题提供了技术参考。