水平井油藏建模统计偏差的处理方法与应用

张改革，佟彦明

(斯伦贝谢中国公司，北京 10015)

目前，随着油田老井产能恢复、致密油气压裂开发增产以及页岩油气的大规模开发[1-3]，水平井在常规油气藏和非常规油气藏的勘探开发中的应用越来越普遍。随着水平井数量的增加，水平井数据在常规油气藏精细表征中起着越来越重要的作用。由于水平井主要设计于储层段，水平段延伸距离长，因此，应用水平井数据参与储层精细表征与建模过程中，可以有效减小井间预测的不确定性，提高砂体连通性的分布预测[4-6]。

但是由于水平井一般针对特定目的层，在特定目的层段内水平层段的数据使得建模过程中目的层段的数据集中度过高，从而数据无法满足统计学的无偏最优估计，因此，应用井上数据统计储层的分布以及孔渗性不能正确反映储层的特征[7-8]。

前人对如何应用水平井资料进行油藏精细描述和建模进行了大量研究，主要可以概括为以下几点：①为砂体平面展布特征研究提供更多的资料来源；②落实目标油藏构造层面和精确落实砂体在纵向上的微构造起伏；③为物性模型提供更多平面上的有效数据[9-10]。水平井资料在以往的建模过程中，主要为帮助定性分析储层在平面分布的非均质性，从而进一步提高储层表征精度，但水平井资料在实际建模过程中的定量统计插值、水平井资料权重统计偏差的处理一直是困扰建模的一个难题，这在过往的研究中没有提出有效的处理方法。

本文从建模过程中水平井资料的定量统计插值出发，阐述分析了水平井资料权重统计偏差的处理方法与适用条件，并应用理论沉积相模型验证了处理方法对于提高储层描述的精度与可行性，优化了定量统计插值中存在的问题。

1 统计偏差处理方法概述

常规直井油藏建模过程中对于采样统计偏差的处理方法，一般为通过计算并赋值一定权重给不同采样密度区域的相应数据，在计算过程中数据比较集中的区域使用较小的权重，而在数据较稀疏的区域使用较大的权重(通过调整数据统计分布实现)[11]。网格去丛聚方法即是通过应用网格的大小来控制不同区域井数据的分布的统计偏差，而对于水平井资料，由于水平井与直井的差异性，内核去丛聚法则能够更好地处理数据的统计偏差。

1.1 方法原理

1.1.1 网格去丛聚方法

网格去丛聚方法为一种常规去权重的方法，这种方法是将地质模型划分为不同的区块网格，然后根据不同区块网格内井上粗化网格的数量来计算每一区块的权重方法。每一区块的权重由区块的大小和形态决定，这由建模数据分析中的I、J、K参数所设定，如图1所示。因此寻找最优的I、J、K参数，对于网格中数据在建模过程中的权重起着重要作用。

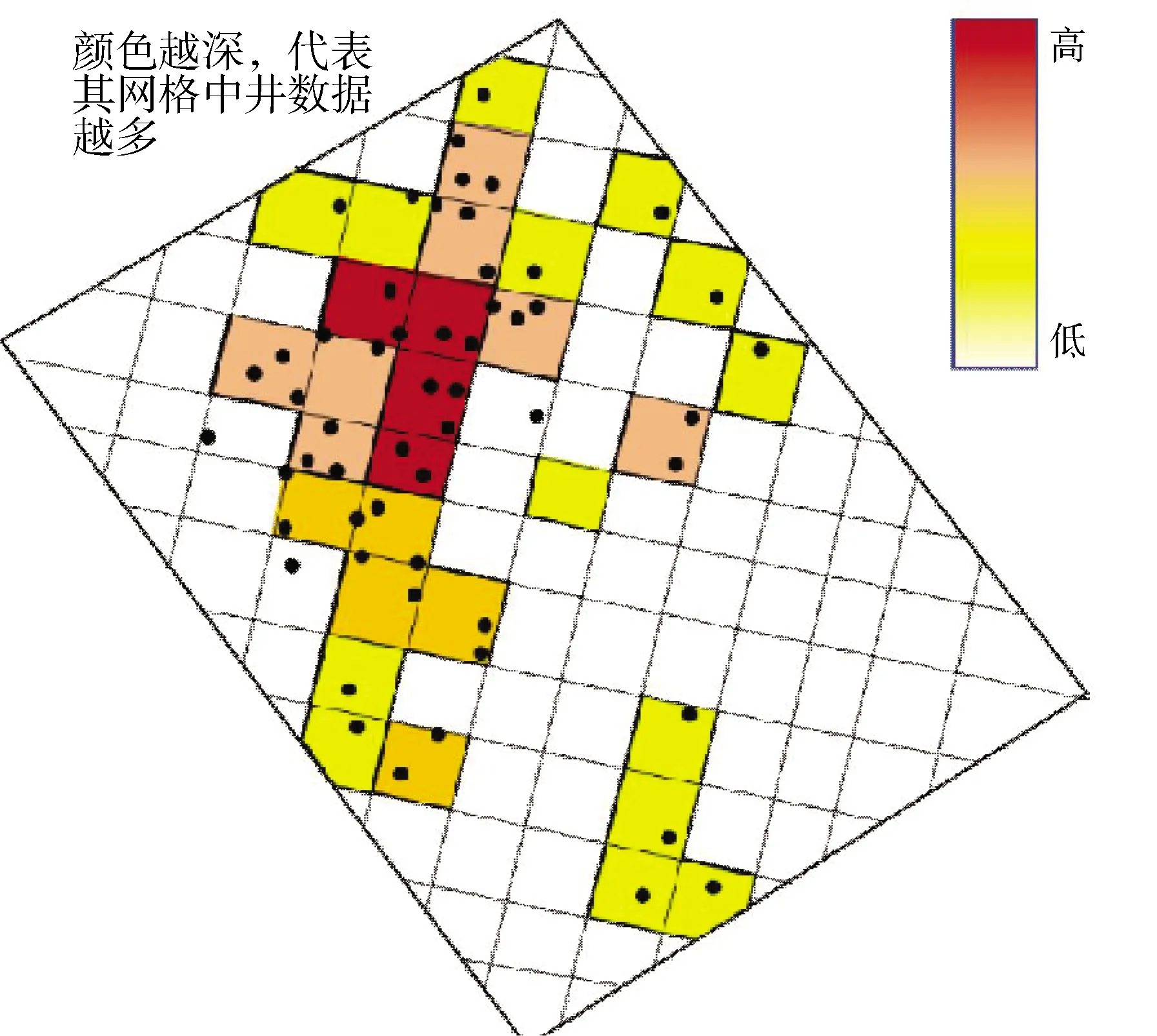
图1 网格去丛聚权重估计方法

其权重系数：α=1/网格中井数据。

1.1.2 内核去丛聚方法

内核去丛聚方法是基于内核密度估计的一种统计去权重的方法。简言之，通过在粗化地质网格卷积平滑的内核函数来估计每个地质网格的密度分布函数。这可以简单地理解为应用内核函数和平滑参数到每一个粗化的地质网格，然后将多个内核函数相加得到其最终的密度分布函数(图2)。去丛聚的权重为其局部密度函数的倒数。

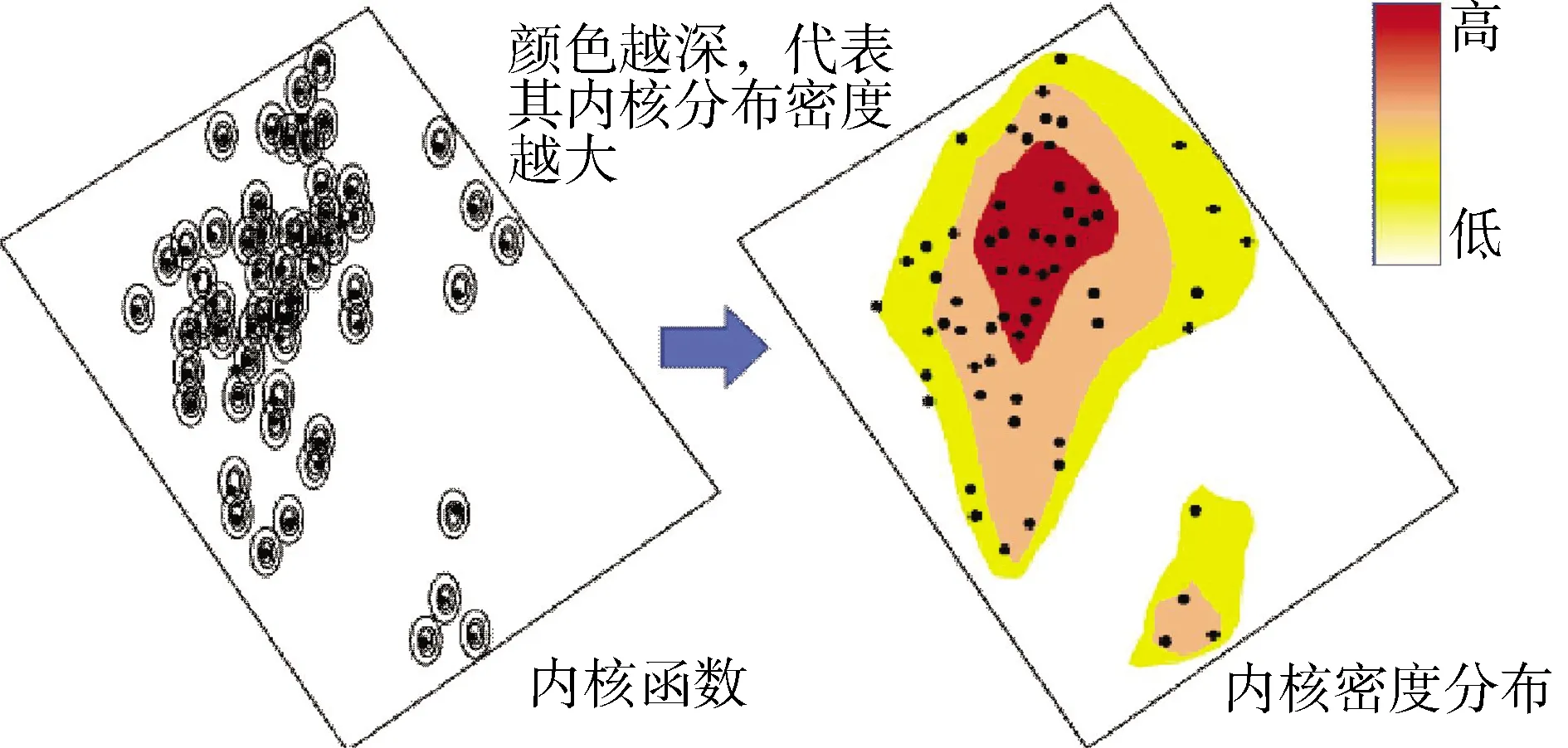
图2 内核去丛聚权重计算方法

在这种方法中，内核去丛聚的网格形态由I、J、K3个方向的平滑参数所决定，通过给予相应的网格数量来实现。内核去丛聚的网格形态决定了地质网格相加平滑的数量和方向，最终影响内核去丛聚的权重系数，如图2所示。

其权重系数：α=1/内核密度分布。

不论是应用网格去丛聚方法，还是内核去丛聚方法，其最终目的是计算测井曲线粗化后井轨迹穿过的每个井网格的权重，然后根据其井轨迹穿过网格的测井曲线的平均值，来优化计算去丛聚后能够更加符合真实地下储层特征的沉积相比例或者储层参数。

其最终去丛聚的平均值计算公式如下：

(1)

αi——井轨迹穿过每个网格的权重系数；

P(ci)——井轨迹穿过的每个网格的平均值。

1.2 水平井去丛聚的适用条件

应用水平井数据进行储层精细表征去丛聚的过程中，由于去丛聚方法会改变原始数据的统计柱状分布和其他统计学特征(例如平均值、方差等)，如果数据不满足去丛聚条件，盲目地使用会造成数据的错误。在进行数据采样之前，重要的一步就是分析查看水平井数据是否会由于井斜的原因导致统计偏差，其分析的数据可以为沉积相、岩相等离散类数据，也可以为孔隙度、渗透率及饱和度等连续型数据。

首先需要评估沉积相分布比例是否会由于水平井输入数据的采样而导致统计偏差：

(1)确保对储层沉积相或者沉积环境了解详细，需要对全区不同沉积相的形态、维度和不同方向的连续性进行详细定量描述。

(2)检查水平井或者大斜度井是否穿过特定目的层的特定沉积相。这些可以影响数据是否会出现采样偏差，如图3所示。

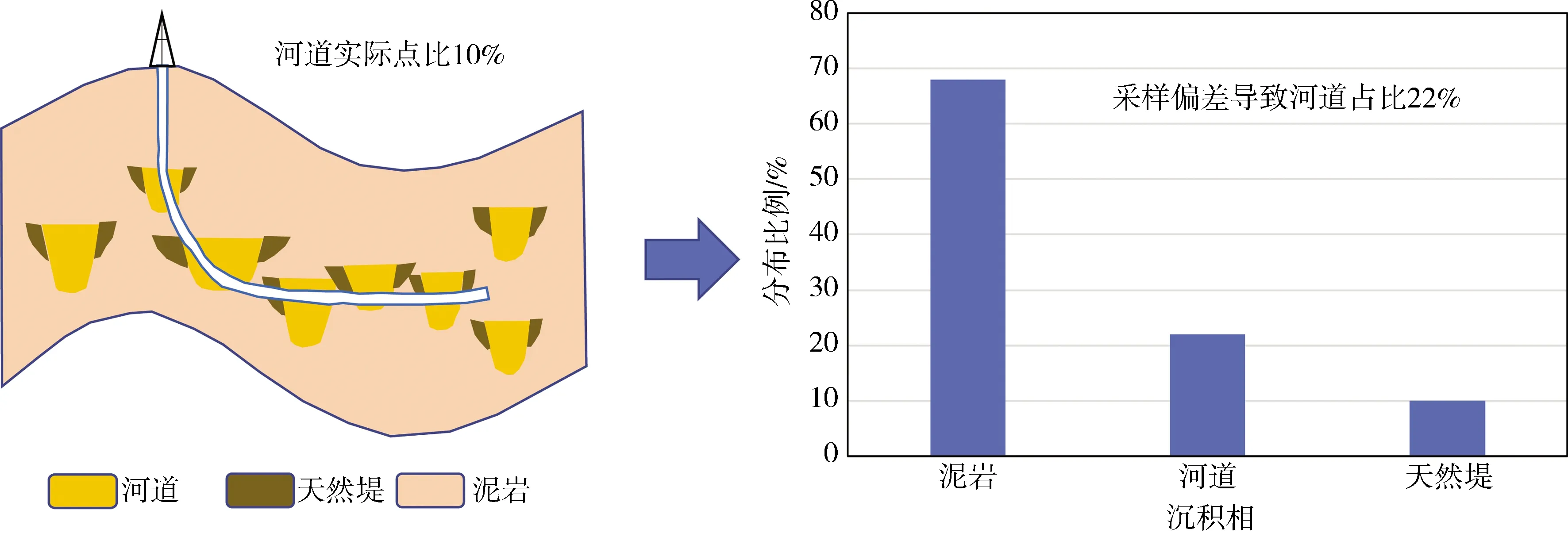
图3 水平井数据采样沉积相分布比例偏差示意图

(3)检查原始沉积相测井曲线是否由于采样而过度估计或者欠估计，并与实际沉积相的已知分布比例相对比。

如果确认水平井数据存在统计偏差，在应用去丛聚处理统计偏差之前，需要检查以下条件是否满足：

(1)是否有足够的数据可以覆盖目标属性分布的整体值域分布。由于权重值只影响不同值域区间内的值，因此去丛聚方法只有当好的研究区和差的研究区都有足够的水平井分布时才可以应用。

(2)没有证据表明地质趋势分布会导致数据的空间采样偏差。如果地质趋势分布导致数据分布出现偏差，则去丛聚方法不能校正此类偏差。在这种情况下，应当首先应用数据分析将原始数据中的趋势进行去趋势分析，再来查看是否会导致出现采样偏差。

如果出现上述两种情况，可以应用3D去丛聚方法来尝试处理其采样偏差，但不能保证其采样偏差可以完全被校正。如果没有明显的证据可以显示输入数据存在采样偏差，或者没有足够的数据可以覆盖全区的数据分布，则在其处理过程中建议采取简单的无权重的处理方法来处理其数据分布。

2 水平井油藏建模难点及质控分析

2.1 水平井油藏建模难点

在页岩气勘探开发或者油气田开发后期，水平井的大量出现可以极大地提高目的储层的油气产量，使得水平井在油气田勘探开发中起重要作用。但是在储层精细描述过程中，由于水平井一般钻遇目的储层的特殊性，使得其大量数据在统计上的分布具有不稳态特征；且由于水平井一般针对特定储层，其储层沉积相及孔渗饱等储层参数的统计往往会大大好于整个区域的实际储层参数分布，从而使得储层沉积相及孔渗饱分布出现过度良好的估计偏差。

在常规储层建模过程中[12-14]，一般以排除水平井数据、抽稀水平井数据或者采用其他间接方法来应用水平井数据进行储层建模，这样会大大降低水平井这类有用数据在储层建模过程中的作用。而网格去丛聚方法由于受网格的方向和大小影响较大，一般对区域分布不均的直井数据的统计偏差处理效果较好，但对于斜井和水平井数据，由于其井轨迹在不同深度的差异性而导致处理结果并不理想。

在水平井地质建模过程中[15-16]，应用Petrel数据分析中的三维内核去丛聚方法[17]直接对原始测井曲线采样进行优化估计，既可以最大限度地应用已有水平井的数据分布，又可以良好地处理水平井数据在建模中的采样偏差，从而提升水平井油藏建模的精度。

在应用3D内核去丛聚方法水平井油藏建模过程中，其难点主要包含以下几点：

(1)水平井的分布是否足够均匀，即在欠估计和过分估计的区域水平井的分布数量要足够，过度的分布不均即使应用去丛聚，其与实际结果差别也会较大。

(2)对不同沉积相的分布或者属性分布有较好的分析了解，以便了解哪些沉积相或者属性是欠估计或过分估计。

(3)3D内核去丛聚密度函数的估计，以及I,J,K密度平滑参数的优化估计。

2.2 技术实现

在应用Petrel进行去丛聚过程中，其主要通过数据分析(Data Analysis)中的Declustering来实现，如图4所示。在其应用过程中，通过估计调整I,J,K网格的大小来估计密度函数，生成的密度函数可以输出来查看质控。在进行沉积相去丛聚过程中，选择主要的沉积相类型，如果对应的沉积相采样完成后为过分估计则选择Minimize proportion，如果为欠估计则选择Maximize proportion，然后再来进行估计。如果应用自动估计的I,J,K网格大小去丛聚的结果达不到要求，还可以选择Specified来进行人为调整。

图4 Petrel Declustering去丛聚设定

在应用Declustering去丛聚对水平井采样数据进行优化去偏差之后，需要在沉积相模拟过程中应用去丛聚优化的沉积相分布比例作为研究区沉积相模拟的最终目标，这样才会在沉积相建模过程中应用去丛聚的数据统计，进一步才能达到优化沉积相或属性建模的结果。

2.3 质控分析

正如之前所说，应用去丛聚方法并不能100%保证能将由于优选采样而导致的水平井采样偏差完全去除，但是可以通过此种方法来优化建模的结果。因此，对于应用去丛聚储层建模结果的质量控制就变得非常重要。

在质量控制过程中，需要将应用去丛聚优化之后的沉积相分布比例或者孔、渗、饱等连续型数据的分布，与之前已知的或者假定的沉积相或者连续型属性分布比例来对比。分别对比应用去丛聚方法之前和之后的建模结果，并与实际估计的沉积相比例或连续型属性对比，来最终确定是否需要应用去丛聚方法的统计结果来建模。

一般可以通过定性和定量两种方法来对结果进行质量控制。

(1)定性质控：对比检查应用去丛聚方法和不应用去丛聚方法建模结果的差异性，分别在三维窗口显示、剖面显示、连井地层对比，或者对某一沉积相、某一地层或者某一区块来分别进行过滤对比显示；此外还可以生成质量可信度图(QA)属性图来对某一层或者某一层的每一个沉积相来进行质控。

(2)定量质控：分别对比应用去丛聚方法和不应用去丛聚方法沉积相比例的柱状分布表、沉积相分布比例的统计数据，优选查看哪种结果更能与实际分析估计的结果相一致，则选择哪种方法。

3 实例分析

由于地下实际沉积相的分布比例一般只有定性的分布类型与分布区域，而整体沉积相比例在区域上很少获得精确的沉积相分布比例，因此，为了能够更好地说明去丛聚方法对水平井数据统计偏差的处理，在此应用理论沉积相模型作为例子，来说明去丛聚方法处理水平井导致的统计偏差在沉积相建模中的作用。

首先在Petrel中做一个理论的河流相模型，此沉积相模型称为Facies_origional(理论沉积相模型)，在模型中不同的小层定义河道相和天然堤相两个相，其各相的分布在不同小层不同区域分布不同，如图5(左图)所示。河道相和天然堤相在工区的西北部较为发育，其相的分布比例如图5(右图)所示，泥岩相占比为74.8%，河道相占比为15.7%，天然堤相占比为9.5%。

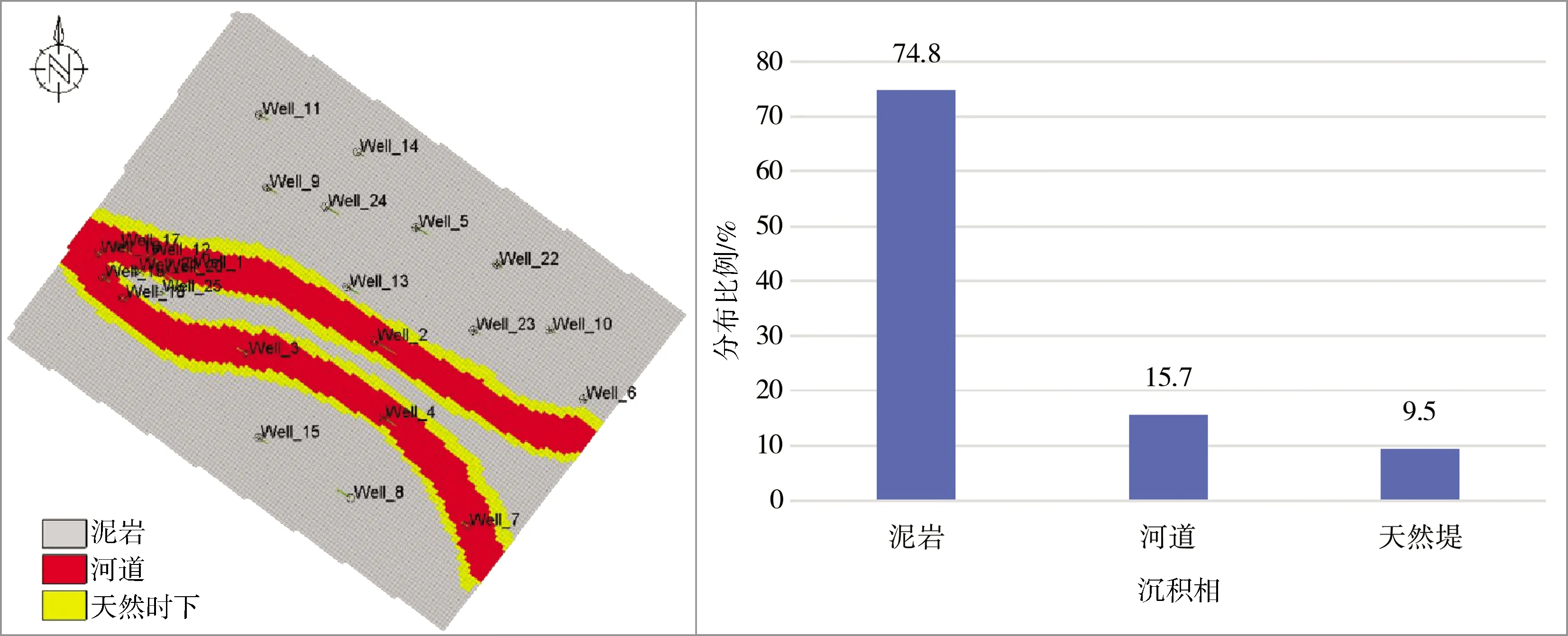
图5 理论沉积相模型、井位分布及各相占比

在此模型中，井的分布、河道平面厚度分布如图6(左图)所示，全区共分布25口水平井，在工区的西部，河道相和天然堤相较为发育的区域，井分布较密，共有9口井。在理论模型的基础上，从模型中生成沉积相测井曲线，并再次粗化到模型中去，应用数据分析功能分析粗化的沉积相曲线。由于井的平面分布不平均，在河道良好发育的西部共计10口井，导致其粗化的相数据出现很大偏差——泥岩的分布占比为49.0%，河道占比为38.0%，天然堤占比为13.0%，如图6(右图)所示。

从测井曲线粗化后各沉积相占比(图6右图)可以发现，由于平面上井在河道发育区分布较多，且水平井轨迹钻遇层段主要为河道和天然堤较为发育的层段(图7)，导致其河道相和天然堤相被过分估计，分别由实际占比15.7%和9.5%被过分估计到分别占比38.0%和13.0%。这就是由于水平井的分布导致的数据统计偏差，去丛聚方法即是为了将这个偏差降到最小。在数据分析中应用3D Declustering方法对粗化的测井曲线进行处理，在粗化的数据中，需要将欠估计的泥岩、过估计的河道和天然堤应用三维内核去丛聚方法重新进行相比例估计。其应用去丛聚方法处理之后的结果见表1。

图6 河道垂向累积厚度平面分布图(左图)及测井曲线粗化后沉积相占比(右图)

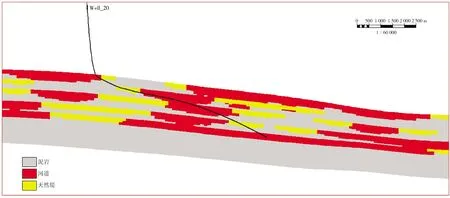
图7 水平井剖面钻遇层段示意图

表1 去丛聚处理前后与实际理论各相占比

通过去丛聚方法对统计偏差的处理，可以发现，处理后的泥岩相分布比例有了很大提高，由原来的49.0%提高到63.7%，而河道相分布比例降为26.9%，天然堤相分布比例降为9.4%。河道相分布比例与实际理论相分布比例还有差距，但相比较原始的38.0%已经有了很大提高；而天然堤相分布比例已经接近实际理论沉积相的分布比例。

应用去丛聚的数据统计结果和不应用去丛聚的统计结果，应用相同的建模地质参数分别进行基于目标的河流相建模以及基于像素的序贯指示模拟，在此分别生成10个模型来进行综合统计，提取10个模型中各个网格出现最多的沉积相(Most of)作为最终相模型，对比其模拟结果的各相统计比例，从模拟的统计结果中可以发现，应用去丛聚方法模拟的各相比例与不应用去丛聚方法模拟的各相比例相比(图8)，其沉积相的分布比例更符合真实的理论沉积相分布，结果更加准确，对于勘探开发具有更符合实际的指导意义。

图8 去丛聚方法与不应用去丛聚方法各相比例模拟结果对比

应用基于目标的河流相模拟方法进行沉积相模拟，比较去丛聚方法的模拟结果与不应用去丛聚方法的模拟结果(图9)可以发现，由于去丛聚方法对过分估计的河道和天然堤进行了优化估计，应用去丛聚方法的河道和天然堤的分布比例更加符合真实的沉积相分布，其模拟结果中河道和天然堤的分布区域更小，多次模拟的结果统计更加符合实际沉积相的分布。而不应用去丛聚方法由于对河道和天然堤的过分估计，使得模拟结果分布比例过高，从而进一步影响全区横向范围和不同小层河道和天然堤的分布更广。

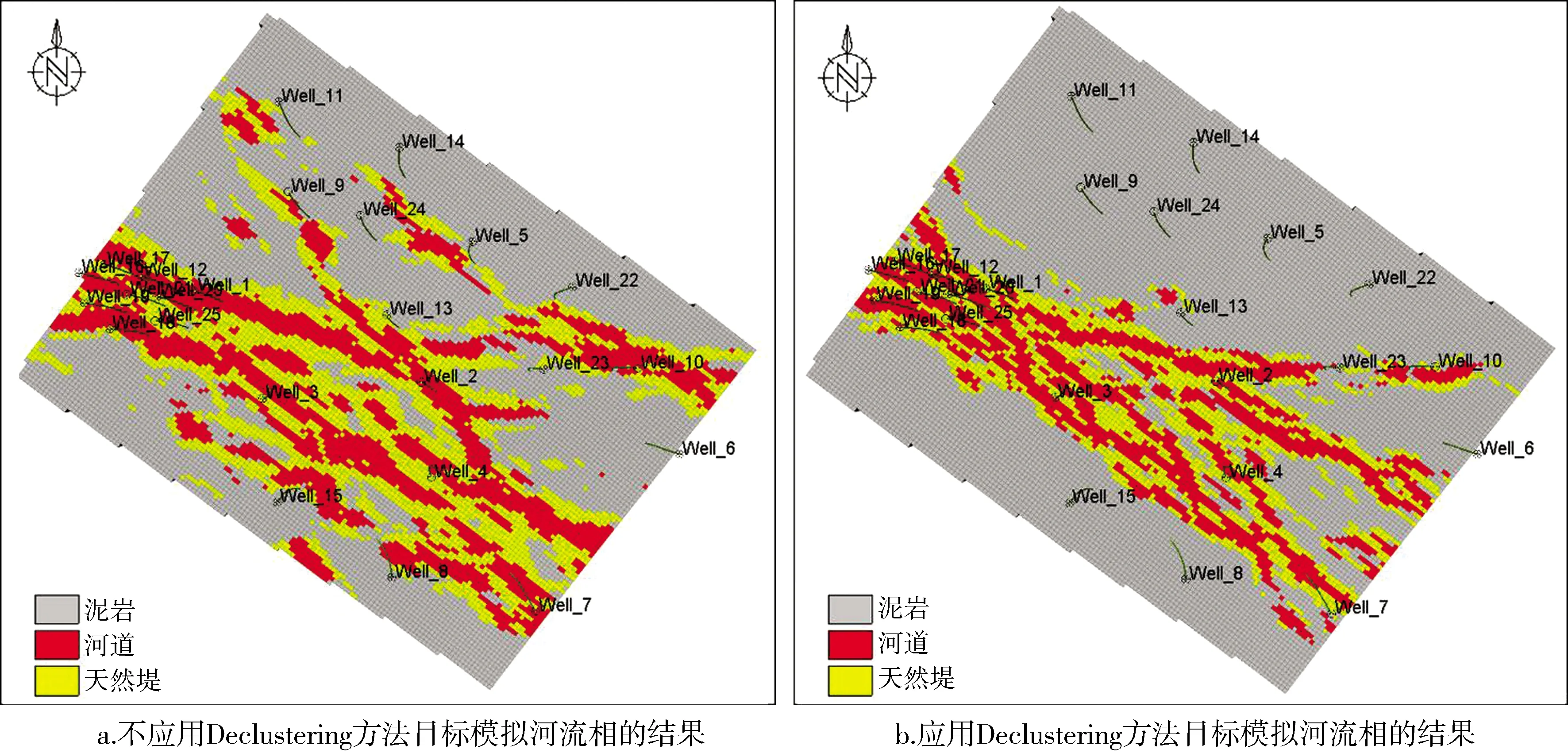
图9 不应用去丛聚方法与应用去丛聚方法沉积相目标模拟结果对比

4 结论

(1)网格去丛聚法(Cell Declustering)适用于由于直井平面分布不均所导致的沉积相及孔渗饱数据的统计偏差，其方法受去丛聚中网格大小和方向参数影响较大，且对大斜度井和水平井的处理效果较差。

(2)3D 内核去丛聚法(Kernel Declustering)应用内核密度分布函数，针对水平井及大斜度井三维油气藏模型中的不同位置和深度的网格计算不同密度函数，生成相应的权重，并对储层精细建模中的统计偏差进行优化再估计，可以大大提高建模中的沉积相与储层参数分布。

(3)应用Petrel中的3D内核去丛聚方法，以理论河流沉积相模型为例，对比分析了应用与不应用水平井3D内核去丛聚方法对建模结果精度的影响。应用3D内核去丛聚方法可以优化提高水平井采样数据沉积相统计结果的精度，使其更加符合真实沉积相的分布比例，河道相和天然堤相占比分别由38.0%和13.0%降低到26.9%和9.4%。

(4)对目标研究区沉积相及储层参数分布的精细研究、水平井的分布是应用Declustering去丛聚处理水平井统计偏差的必要条件，只有在对目标区充分了解的基础上才可以更好地应用去丛聚来处理水平井储层建模中的统计偏差问题。