机器人快速示教方法及示教点位姿变换的研究
2021-01-13韦祖杰
韦祖杰
(中国重汽集团柳州运力专用汽车有限公司,广西 柳州545112)
0 引言
近年来,工业机器人在生产制造业中扮演的角色越来越重要,越来越多的工业机器人取代了原来工人的位置,工业机器人代替人完成任务已成为一种必然的趋势[1]。要想使工业机器人完成工作,必须预先对机器人进行示教,所谓示教通俗来说就是给机器人发出指令,让机器人按照指令一步一步来完成预想的工作任务。目前,机器人示教工作主要是借助于工人操作示教器来完成的。这种示教方法存在着示教效率低,且过程复杂,并且要求操作人员需要掌握一定的工业机器人的使用操作知识等诸多缺点。如此一来,提高机器人作业精度、工作效率以及使示教过程不再复杂也就成了当前迫切需要解决的问题。伴随着视觉技术的成熟应用使得这一问题得到了很大的改善。
1 目前常用的示教方法
1.1 示教器
示教器也叫示教盒,操作人员可通过示教器来对机器人进行示教,使用示教器编写程序,示教结束后,操作人员可通过运行已编写的程序即可实现示教再现。目前,大多数企业在工业自动化生产中需要进行周期性的重复工作,这就需要机器人完成示教再现功能,通过示教器进行示教编程即可完成。示教器编程存在以下优缺点[2]:
优点:编程门槛低、简单方便、不需要环境模型;对实际的机器人进行示教时,可以修正机械结构带来的误差。
缺点:
(1)示教过程比较复杂繁琐、且工作效率较低。
(2)示教人员通过目测进行寻位,导致了精度的不精确性。对于路径复杂的示教工作,示教编程达不到想要的结果。
(3)示教器种类繁多,操作人员需学习大量东西。
(4)在示教过程中,容易对设备造成损伤,同时对人身安全具有一定的威胁。
(5)进行示教时,我们需要通过操作机器人来进行。
1.2 拖动示教
示教器示教的方式,存在较多的缺陷。为了能够克服这些缺陷,研究人员提出了一种新的示教方式即“拖动示教”。拖动示教,其主要的操作就是拖动,拖动简而言之就是直接拖动机器人的各个关节,运动到想要的位置姿态,然后把该位置记录下来,机器人会把刚才运动的信息保存到上位机的存储器中,之后机器人再从上位机中读取相应的信息并进行示教。相较于传统示教器方式,拖动示教能够更加简单实现,而且示教所需要的时间会大幅度的缩减,效率也能够有较大的提高,其操作的门槛要求较低。拖动示教是一种比较有发展前景的示教方式。
2 示教点的齐次变换
2.1 机器人末端执行器相对于机身坐标系的齐次变换
根据D-H法建立坐标系可得出相邻连杆(图1)间变换矩阵为:
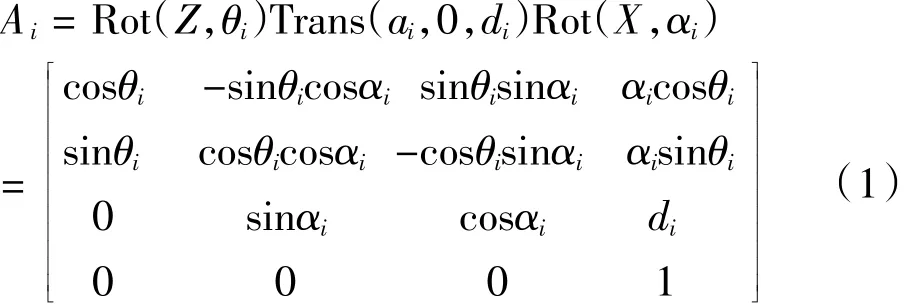
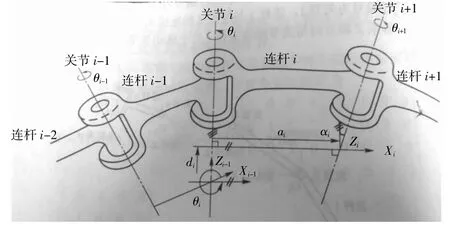
图1 相邻连杆坐标[3]
其中,θi为绕Zi-1旋转θi角,使Xi-1转到与Xi同一平面内;di为沿Zi-1平移一段距离di,把Xi-1移到与Xi同一直线上;Ai为沿Xi轴平移一段距离ai,把连杆i-1的坐标系移动到使其原点与连杆i坐标系原点重合的地方;αi为绕Xi轴旋转αi角,使Zi-1转到与Zi同一直线上[3]。
2.2 工具坐标系的标定(六点法)
确定机器人工具坐标系相对于机器人末端连杆坐标系的齐次变换即为工具坐标系的标定[4]。工具坐标系的标定方法多种多样,其中外部基准法和多点标定法是目前比较常见的标定方法。
机器人各关节坐标系建立示意图如图2,xoyozo机器人的基坐标系{B}=xoyozo;末端坐标系{E}=x6y6z6;工具坐标系为{T}[5]。为机器人末端坐标系相对于基坐标系的齐次变换矩阵,为工具末端坐标系相对于机器人末端坐标系的齐次变换矩阵,为工具末端坐标系相对于机器人基坐标系的齐次变换矩阵。三个矩阵之间的变换矩阵为:

其中根据机器人正向运动学求解得
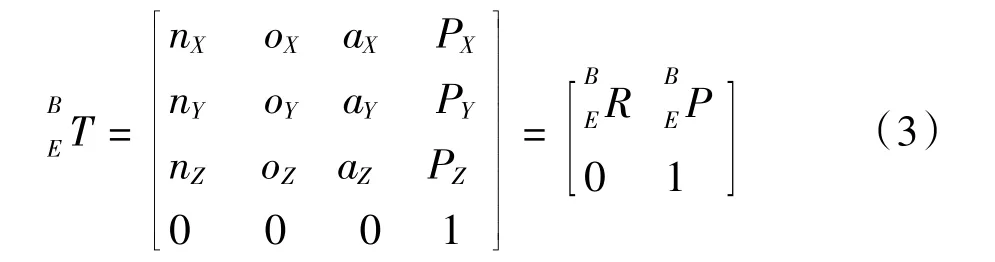
其中为机器人末端坐标系相对于机器人基坐标系的旋转矩阵,为位置矢量。
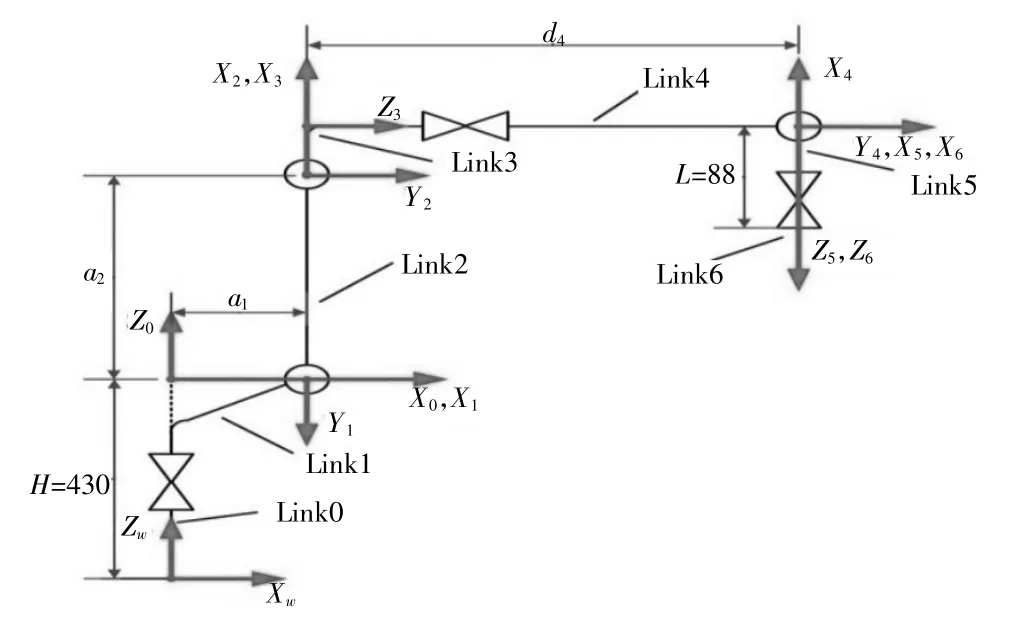
图2 六关节坐标图
2.2.1 工具坐标系的位置标定
采用六点法标定TCP,所取标定点如图3所示。在工作台上放置一个测量规尺,操作机器人以不同的姿态去点测量规尺尖端。P1为随机给定的初始点,P2、P3为随机取的 2 个点,P1、P2、P3三个点在同一平面内,P4的Z轴与测量规尺的Z轴在同一直线上。

图3 取点示意图
根据式(2)可得

因为P1、P2、P3、P4为不同姿态下标定参考点,由式子(4)变形可得:
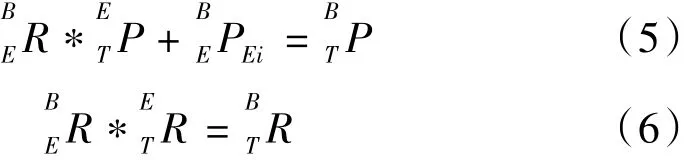
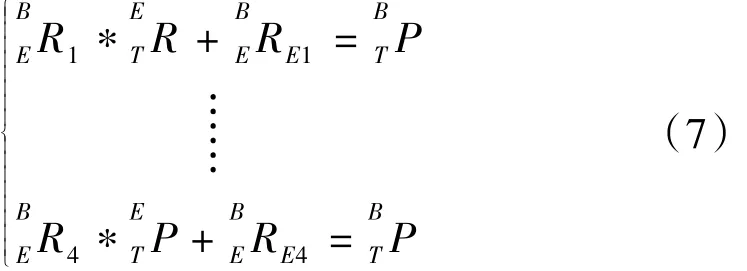
结合式(6)进行以下的变换:P2-P1,…,P4-P3,即
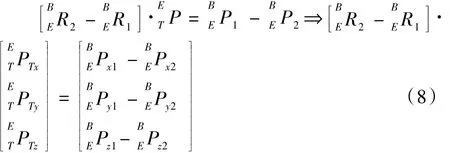
依次类推可得:

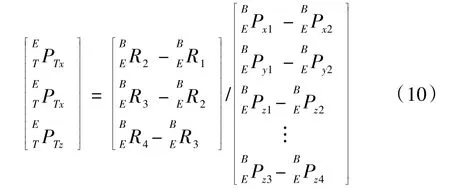
2.2.2 工具坐标系的姿态标定
如图4所示,以P4为第一点,操作机器人先沿+x方向平移一段距离得点P5,然后再回到P4,在沿+z方向平移一段距离得点P6。
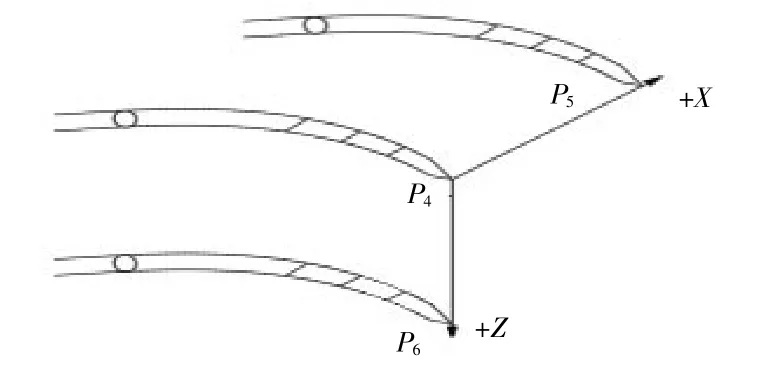
图4 取点示意图
已知都相等,已知。P4与P5之间的向量关系即为工具坐标系沿+x方向的向量。工具坐标系的x轴轴向向量为:

同理可得工具坐标系的z轴轴向向量为:
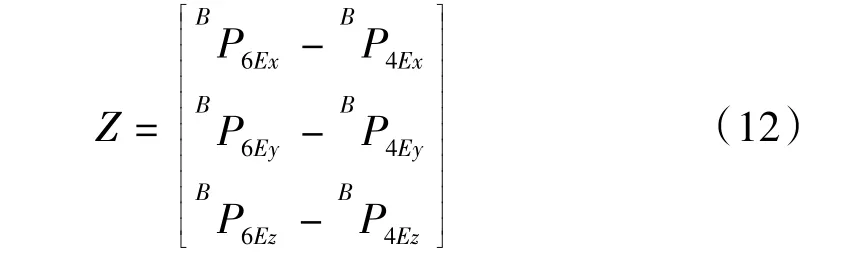
BP4E、BP5E、BP6E分别为P4、P5、P6相对于基坐标的位置。
根据右手定则有:

将式(11)和(12)代入Y=X·Z,并对其进行单位化矩阵变换。即可得出工具坐标系相对于机器人基坐标系的姿态。由(6)式,经过矩阵计算,即可求出旋转关系。
综上,即可求得工具坐标系相对于基坐标系的齐次变换。
2.3 工具坐标系到相机坐标系之间的转换(手眼标定)
工具坐标系与相机坐标系之间的转换常用手眼标定,手眼标定的过程即为求解齐次变换矩阵的过程。目前常用的求解方法主要分为两大类:线性法和非线性法[6]。
本次采用了传统的手眼标定算法两步法,传统手眼标定又有Eye-to-hand和Eye-in-hand两种方式之分[7]。Eye-to-hand是摄像机固定安装在机器人本体外的某一空间位置,不随机器人的运动而运动。Eye-in-hand是摄像机固定安装在机器人末端执行器,相机会跟随工业机器人的运动而运动。传统两步法本次是基于Eye-in-hand系统的方式进行标定。标定主要思路为借助某空间参考点,操作机械手以不同的位姿观察该点。
标定过程,设选定参考点的坐标系为{Cobj},相机坐标系为{C},操作机器人从P1运动到P2,图5为平移前后的坐标系关系示意图。
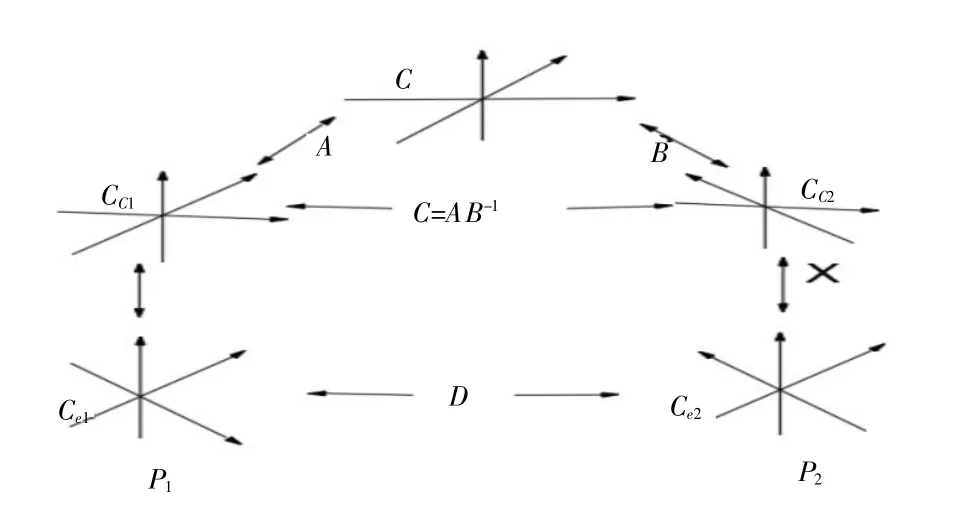
图5 相机平移前后坐标关系图
CC1、CC2为从P1运动到P2相机前后所在两位置对应的坐标系,Ce1、Ce2为从P1运动到P2机械末端执行器前后两位置所对应的坐标系。在CC1、CC2两位置根据摄像机标定法可求得相机的内外参数[8]。外参即为相机坐标系到参考点坐标系之间的转换关系,记为Ra、ta。用R、t表示机器人工具坐标系与相机坐标系之间的变换关系。如图有CX=XD,求解X的过程就是手眼标定过程。X即为我们想要的手眼标定参数。图中的各相对位置的关系A、B、C、D、X都是 4×
4 齐次矩阵的形式。
将CX=XD方程中的每一个 4×4矩阵都写成以相应的旋转矩阵以及平移向量组成的形式,并将其展开得到下式:
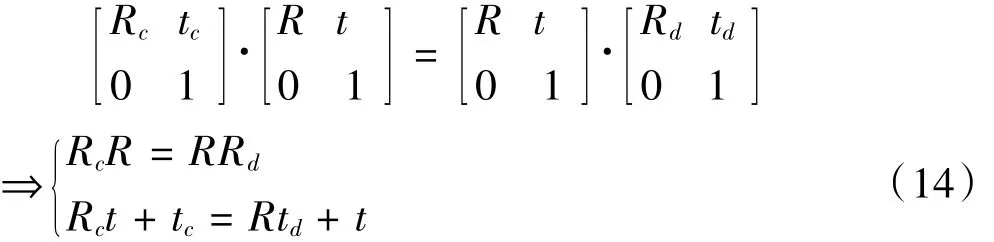
由式子(14)可知方程有无穷多解,为了确保方程有唯一解,则确定两组数据甚至两组以上的数据。为方便计算,在此取两组数据,代入式子(14)得:
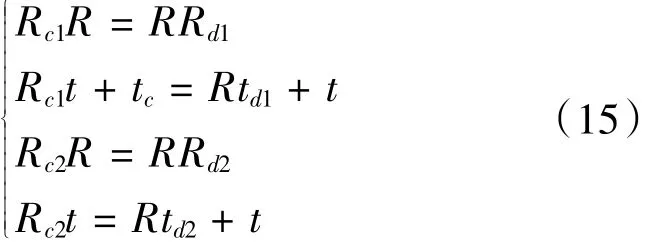
在(15)式中,Rc1、tc1、Rc2、tc2分别是摄像机在P1、P2处的参数,根据摄像机标定可求出其外部参数即旋转矩阵和平移向量;Rd1、td1、Rd2、td2分别为机器手在P1、P2处的参数,该参数一般都是从机器人控制器获取的;R、t为手眼矩阵中的旋转矩阵与平移向量,也就是要求的未知量。在(15)式中旋转矩阵都是3×3矩阵平移向量是3×1矩阵。根据摄像机标定可求出了相机的内外参数,在内部参数已知的情况下,根据(15)式并运用了旋转矩阵的性质,即可求出旋转矩阵R,再将所求的R代回到(15)式即可求得平移向量t。在上述的算法之中,由旋转矩阵求平移向量的过程称为手眼标定传统两步法。
3 立体视觉技术的应用
经过几十年的发展,立体视觉技术在机器人导航、航空测绘、医学成像、和工业检测等领域中得到了广泛的应用。目前基于立体视觉技术的机器人示教方式在焊接领域中应用较为广泛。基于立体视觉技术的机器人示教装置(示教笔)已经出现,通过用示教笔进行取点,通过立体视觉技术将示教笔的运动轨迹传输至电脑终端并生成相应的代码程序,使机器人能够准确无误的跟随示教笔的轨迹进行工作。其示教过程简便,对操作人员的要求较低,而且能够确保较高的精度。
4 小结
通过对示教点轨迹的坐标转换,能够进一步了解到机器人是如何通过立体视觉技术来完成示教,无论是示教器还是拖动示教,机器人取点的方式都比较复杂,对操作人员的要求较高,且精度较低。随着立体视觉技术的发展,基于立体视觉技术的机器人快速示教方式得到了广泛的应用。
