基于智能算法的多目标路径规划
2021-01-13李传发杨舒音
李传发 ,杨舒音 ,李 末 ,孟 妤
(1.大连理工大学机械工程学院,辽宁 大连 116024;2.中机科(北京)车辆检测工程研究院有限公司,北京102100;3.大连益利亚科技发展有限公司,辽宁 大连116000)
1 研究背景
随着着互联网技术的发展,物联网应运而生,其用途十分广泛,遍及智能交通、仓储物流、环境保护、工业检测等多个领域。随着快递等服务业的快速发展,物联网在仓储物流中的应用也是起着非常大的作用,比如中国的一些大型港口已经实现无人化,一些快递的中转地依靠机器人进行快递的分拣。在实际的应用场景中机器人有时需要从起点出发去不同的地点完成多个任务再回到起点,而为了减少机器人在路径上花费的时间,需要算法来规划其路径,使机器人在执行任务时经过最短路径。
本文所提出的算法所要解决的问题即当机器人需要从起点出发,路经多个需要停留作业的地点(目标点),然后回到起点时,规划出机器人所走过的最短路径。此类问题在现实中有很多应用的场景,因为我们有时需要的不只是从起点到终点两点之间的路径寻优,而是从起点到多个目标点的路径寻优。比如外卖的配送、快递的邮寄等,他们都是从一个起点出发,需要经过多个目标点再回到起点。而目前的路径寻优基本是单目标点的寻优即从起点到终点的路径规划,比如经典的A*算法、D*算法以及本文用到的JPS算法[3]等,在这些算法的基础上进行改进后,使得路径的规划更加高效,比如在A*的基础上进行改进的算法如:吴鹏等人[4]提出的双向 A*算法对比 A*算法效率上最大提升了73.4%,对A*算法的寻路策略进行优化,在保证原有算法路径平滑性和安全性的基础上,同时提升了机器人的寻路效率和实时规划能力;李冲等人[5]提出了一种单边矩形扩展 A*算法,通过受迫扩展规则,简化了终止条件,提高了寻路效率和路径质量;赵晓等人[6]提出跳点搜索方式以改进A*算法,降低对不必要节点的计算,从而使得寻路效率得以提升;Goldberg等[7]在启发函数的精准度方面加以改进,以提高寻路效率,但由于过于侧重速度提升使得空间复杂度增加。以上研究工作都是在路径规划的效率和路径平滑性上进行了研究。
在规划多个目标点之间的最短路径时,机器人经过目标点之间的先后顺序也是影响因素之一,根据上述算法的原理,这些算法只能规划出两个目标点之间的最短路径,所以在解决多目标路径规划问题时,上述算法就无法单独解决此类问题。为此,本文提出了在多目标路径规划时,可以先求解两两目标点之间的最短距离,再求出多个目标点在最短路径中所处的次序,即以JPS算法求解出两两目标点之间的最短距离,再使用蚁群算法求解出依次经过各个目标点的顺序,这样就可以实现由算法规划出一条经过多个目标点的最短路径。经验证可以很好的应用于多目标路径规划,在不同的环境下使用不同的超参数从而使算法整体的效率和准确性都大大提高。
2 智能算法
2.1 问题模型
本文的问题模型示例如图1所示,此实际环境中常为机器人需要从点1出发,在遍历其余四个目标点后,再回到起始点1,为了提高机器人的工作效率,要规划出一条最优路径。为了直观的显示未优化的路径与优化后的路径的效果对比,将由点1、4、5组成的三角形设为等边三角形,由点1、2、5组成的三角形为钝角三角形,且位于点5处的角为钝角。

图1 示例目标点
如图2所示,所采用的策略为按照目标点序号的大小进行遍历,采用这种方法时所经过路径的没有进行优化,与图3经过蚁群算法优化后的路径进行对比可知,后者的路径长度减少了3.5,当目标点增多时,经过在第四章的对比,这个结果会更加显著,所以对路径进行优化可以显著的提高机器人的工作效率。

图2 按序号遍历

图3 按蚁群算法优化后遍历
在实际的环境中,可能还会有障碍物的存在,不能直接得知两两目标点之间的最短距离,所以两个目标点之间的距离和路径也需要进行规划。而JPS是Daniel Harabor与Alban Grastien提出的一种基于A*的算法,它在栅格无权地图的搜索性能要强于A*算法,本文选用了JPS算法来降低整体算法的时间复杂度,因为在目标较多时,路径搜索的运算量也是呈指数级上升,所以找到一个低时间复杂度的算法显得尤为重要。
2.2 算法思路
(1)算法的整体思路为:输入所有目标点的坐标,利用JPS算法快速的计算出将两两目标点之间的最优路径,将这些路径的具体信息(如栅格地图中,路径所经过方格时,所有方格的中心坐标的集合即为具体信息)和路径的长度分别存储在各自的列表中,然后将存有各个目标点之间路径长度的列表,输入到蚁群算法中,计算出最优的路径中目标点的排列顺序,并返回到一个列表中,结合存有两两目标点之间路径具体信息的列表。就可以得出一次遍历所有目标点的具体路径。算法的总体流程框图如图4所示。
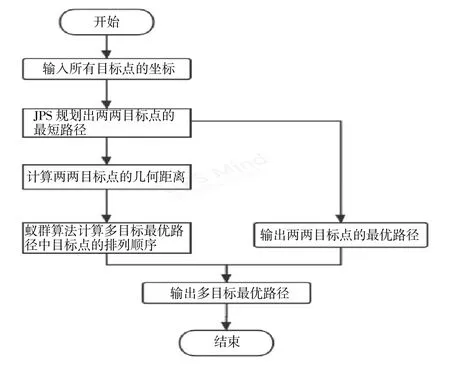
图4 流程框图
JPS的实现方式如下:从起点先随机寻找一个方向进行搜索,在搜索时为两个循环嵌套,在斜向上前进一个单位后,分别在此方向的横向和竖向进行搜索,比如选择(1,1)方向进行搜索时,那么在横向与竖向的搜索方向分别为(1,0)、(0,1),当在横向搜索与竖向搜索结束时,进行下一循环,即进入下一个状态的斜向搜索。当横向、竖向的下一位置为障碍物、边界或终点时停止横向与竖向的搜索,即停止循环进入斜向搜索循环,同样的,当斜向搜索下一位置为障碍物或边界时,一个循环至此结束,并将所有的强制临点,与强制临点的父节点加入到openset列表中,然后再在起点选择一个与之不同的方向进行循环,这样就可以遍历所有图的节点并最终可已找到一条起点与终点之间的最优路径。
强制临点的判断:如图5所示为直线方向在判断强制临点时,需要判断在p(x)上下两个位置,如果有障碍物则将其斜上方的点当做强制临点加入openset列表中,并将斜上方节点的父节点设为当前节点,一同加入openset列表中、diagonal方向在判断强制临点时,需要判断当前节点的下方与左方是否为障碍物,如x点下方有障碍物,则x的强制临点为左下方的节点,同样的将其加入到openset列表中,并将其设为x的子节点,这些节点再加入到openset列表中。

图5 横向搜索
将JPS与蚁群算法相结合的计算路径长度算法为计算由JPS规划出两两目标点之间的几何距离,因为蚁群算法需要在给定了两两目标点的距离后,才能开始优化,所以需要一个函数将JPS中各个目标点的具体路径(储存在图7的列表l1中)进行计算得出两两目标点之间的距离(储存在图7的列表l2中),再传入蚁群算法中。流程图中的第二个循环内的判断中点i与点j的距离L加1或加1.4(图6)当机器人沿栅格的斜边走时是其沿直角边走大约是距离的1.4倍,是根据点i与点j之间路径中相邻两点位于水平线或在对角线的位置为判断依据。经过其流程图为:
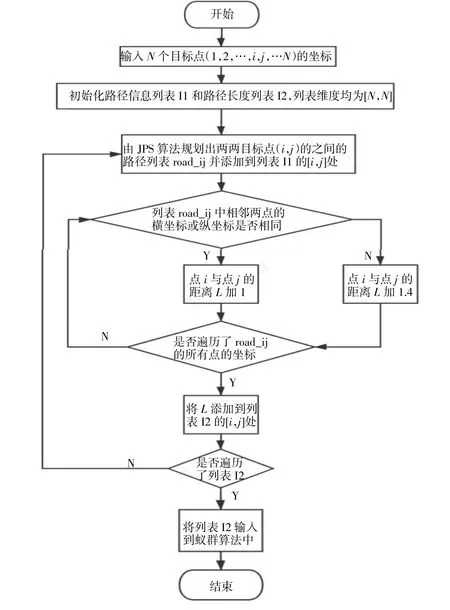
图7 计算路径长度算法
3 超参数测定
蚁群算法(ant colony optimization,ACO),又称蚂蚁算法,是一种用来在图中寻找优化路径的机率型算法,它由Marco Dorigo于1992年在他的博士论文中提出,其灵感来源于蚂蚁在寻找食物过程中发现路径的行为,蚁群算法是一种模拟进化算法,初步的研究表明该算法具有许多优良的性质[1-2]。
将计算出的各个目标点的路径长度传入蚁群算法中,然后利用蚁群算法进行计算。首先将参数进行初始化,然后开始使蚂蚁分别对一条路径进行探索,首先随机选择一个目标点,然后计算此目标点到其他未到达过得目标点的转移概率,选择下一城市的方式为轮盘赌的方式,然后在所有目标点之间进行循环,直到一只蚂蚁将所有的城市都遍历完毕,并将其所路经的距离进行计算,记为totle-distance,在所有蚂蚁循环完毕以后,将路过路径最短的蚂蚁记为best-ant,用于返回最优路径,在所有蚂蚁遍历过所有路径一次后,更新路径上的信息素,并进入下一次循环。流程图如图8所示。
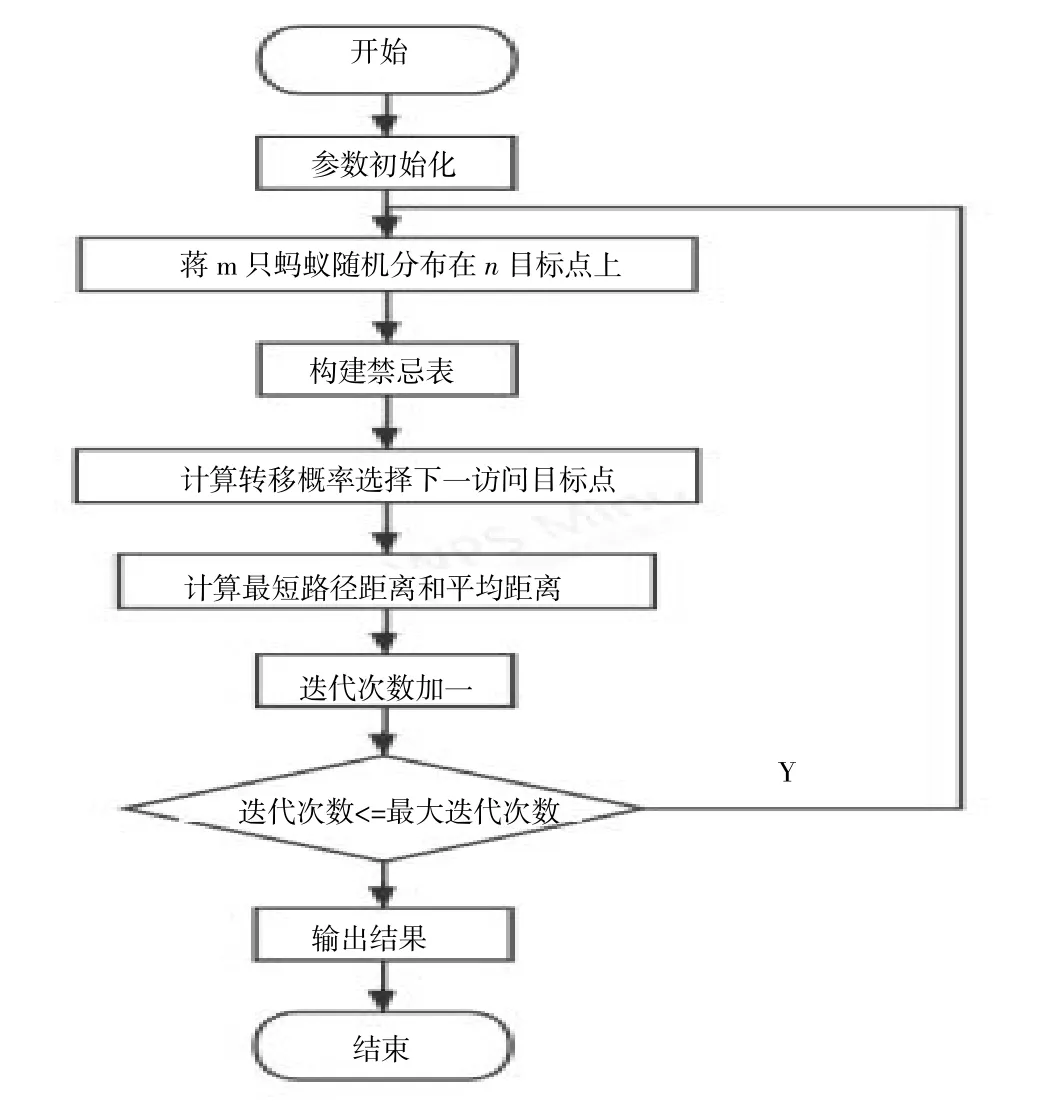
图8 蚁群算法规划目标点顺序流程图
在蚁群算法中需要对超参数进行预先设定,而一般人们对超参数的设定往往根据经验进行设定,但是对于不同的问题,不同的超参数会影响算法的整体效率,所以作者对本算法用到的模型进行了超参数的测定,使算法可以在特定的环境下更有效率。
图9中纵坐标为路径的最短距离,横坐标为迭代次数,从上到下,从左到右依次分别为10、20、30只蚂蚁进行优化的曲线。由图9中可以看出当目标点的数目在20个左右时,蚂蚁的数量为20左右时,路径就可以达到最优,当蚂蚁的数目再增加只是减少了迭代次数,但是目标点数目的增加对会使算法的效率降低,所以21目标点设置20蚂蚁进行迭代最优。
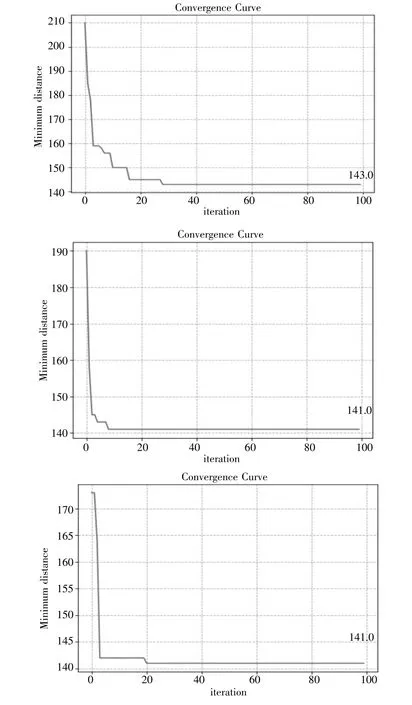
图921 目标点收敛曲线
图10从上到下,从左到右依次分别为30、50、70只蚂蚁进行优化的曲线,可以看出当目标点数为51时,蚂蚁数量为50时,就能找到最优路径。由上面两组图我们可以看出目标点的数目和蚂蚁的数量相当时,算法就可以达到一个很好的效果。
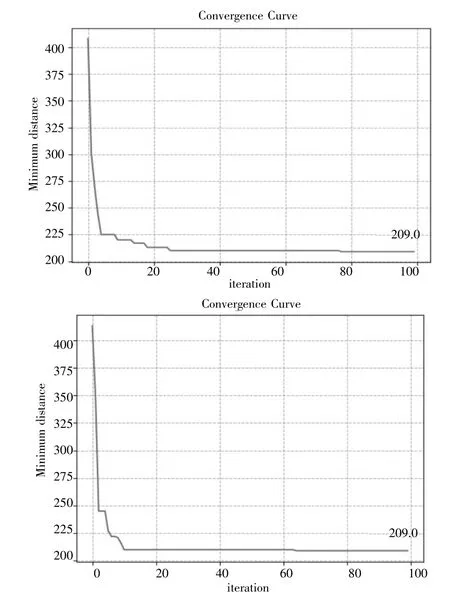
图1051 目标点收敛曲线
4 模拟实验
为了验证本算法的可行性,在python3.7的平台环境下进行了仿真实验,分别仿真了21个目标点和51个目标点,通过实验验证了本文所提出的算法的可行性。实验结果如图11-14所示:其中灰色的方块代表机器人[智能体]要到达的目标点,灰色实心格子为障碍物,灰色空心格子为可移动路径,灰色的实线为智能体的移动路径。

图1121 目标点路径寻优

图1221 目标点路径

图1351 目标点路径寻优

图1451 目标点随机路径
由图11与图12和图13与图14对比可以看出经过优化后的路径比没有优化的路径要短,经过计算得知图11的路径总长为75.8,图12的路径长度为76.2;图13的路径总长为182.4,图14的路径长度为279,图12的路径经过了简单的目标点顺序规划,如图15所示,左右两图目标点的坐标相同,但是两图中点2与点3的顺序不同,两图的遍历顺序都为点1到点2到点3到点4,这时可以看出右图的路径长度明显小于左边的长度。这是因为当遍历路径时当由交叉线时,路径的长度就会变大,所以可以在连接各个目标点时尽量避免路径重叠可以缩短路径,但是此方法费时费力,所以需要蚁群算法来帮助规划,当没有进行任何规划时,如果只是让机器人随机的遍历目标点,由14图可以看出路径明显的增多。所以经过对比可以看出此算法可以很好的应用于多目标点的路径寻优。
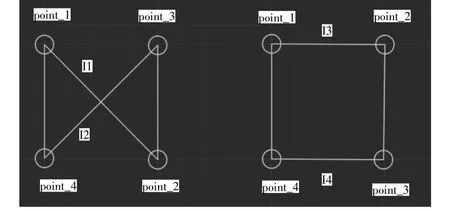
图15 路径规划
5 结语
本文所选用的蚁群算法和JPS算法很好的解决了所目标路径规划的问题,作者对整体的算法进行了设计,对蚁群算法中的超参数进行了仿真,使得算法的效率进一步提升。要想将算法应用到现实情况中,还需要对算法进一步优化,因为算法的路径的拐点过于曲折,所以作者下一步将会对路径进行优化,使其可以应用到实际情况中。
