城市场次降雨径流污染负荷快速估算方法*

2021-01-12何胜男陈文学廖定佳穆祥鹏

湖泊科学 2021年1期

何胜男，陈文学，廖定佳，周瑾，穆祥鹏

(1：中国水利水电科学研究院，北京 100038) (2：中国水利水电科学研究院流域水循环模拟与调控国家重点实验室，北京 100038) (3：深圳市水文水质中心，深圳518055) (4：深圳市东部水源管理中心，深圳 518172)

根据《2018年中国生态环境状况公报》，2018年全国地表水中Ⅳ类和Ⅴ类占比达22.3%,劣Ⅴ类占比6.7%,全国地下水水质监测点中Ⅳ类占70.7%，Ⅴ类占15.5%[1]，我国地表及地下水面临着不同程度的污染. 水污染控制和水环境保护的关键是控制污染物总量的排放，而其基础和关键是定量水体污染负荷总量[2]. 对于城市水环境而言，城市降雨径流污染是城市水质恶化的重要原因之一[3-4]，定量计算城市降雨径流污染负荷，可为城市水环境治理和污染控制提供科学依据.

定量非点源污染负荷计算最早是美国在1960s-1970s开展的[5]，中国始于1980s[6]. 目前，定量城市降雨径流污染负荷的计算方法较多，如浓度法[7-9]、统计方法[10]、推算方法[11]、反算方法[12-13]，这些方法大多用于估算年污染负荷，通常需要监测多场场次径流污染负荷，监测难度和工作量大、费用高，且估算精度与监测的降雨场次有关. 目前，关于估算场次降雨径流污染负荷研究相对较少. 随着计算机的高速发展，数学模型的优势逐渐显现. 目前，通用的计算模型较多，如SWMM[14]、STORM[15]、DR3M-QUAL[16]、SLAMM[17]、HydroWorks[18]、HSPF[19]、MOUSE[20-21]等. 数学模型是定量分析非点源污染负荷的重要手段之一，通常利用有限场次降雨的监测数据便可估算研究区降雨径流污染负荷. 数学模型存在的主要问题是建模和参数率定时间较长，并且在预测分析平原城市的污染负荷时存在子流域划分困难、河道流向难以确定等问题[22]，导致径流量计算偏差较大，增加了污染物负荷计算的难度和预测精度.

为此，本文提出一种适用地区较广的快速估算场次降雨径流污染负荷的数学模型，即以污染物累积-冲刷理论为基础，提出了“特征面积”的概念和计算公式，构建了场次降雨径流污染负荷数学模型，并结合多个案例，对数学模型的有效性、预测精度和适用性等方面进行评价，以期为场次降雨径流污染负荷的计算提供一种快速估算方法.

1 场次降雨径流污染负荷估算方法

地表径流污染负荷是指由降雨引起地表径流排放的污染物总量，其中由一场降雨引起的称为场次降雨污染负荷，由一年中多场降雨引起的称为年污染负荷[23]. 对于径流污染负荷，有学者采用径流量与对应污染物浓度的乘积进行计算，但数据需要现场监测，难度较大；另有学者通过多年监测数据统计出的估算模型进行计算，所需资料少，应用简便，如Schueler提出了城市开发区年地表径流污染物计算模型[10]，该模型中污染负荷与地表径流系数、汇水区面积、降雨量和污染物径流量加权平均浓度呈正比. 地表径流系数和污染物径流量加权平均系数对模型的精度影响甚大. Thomson等[24]研究表明，污染物径流量加权平均浓度的准确估算至少需要15～20场降雨径流观测数据.

污染物累积过程和降雨冲刷过程是决定降雨径流污染负荷的两个重要过程，描述累积过程的模型主要有线性、指数、对数等形式，其中以指数及一些变形形式相对比较成熟，而基于反映动力学假设的冲刷过程模型被人们广泛使用[25]. 应用广泛的SWMM模型中采用的是污染物线性累积模型和指数冲刷模型[26]，见公式(1)和(2). 该模型能较好地反映污染物负荷机理.

(1)

式中，C1为最大累积量，kg/m2；C2为半饱和常数(达到最大累积物一半时所用的时间),d；t为晴天时间，d.

W=c1·qc2·B

(2)

式中，c1为冲刷系数；c2为冲刷指数；q为单位面积径流速率，mm/h；B为污染物累积总量，kg/mm.

本文以污染物累积-冲刷理论为基础，提出“特征面积”概念，以表征污染物在各类土地上的污染负荷特性即污染物累积特性和冲刷特性. 污染物累积特性用权重系数表示，即以污染物在各类土地上的最大累积量作为各类土地面积的权重，用以表征污染物累积强度，并以归一化的方式计算特征面积的权重系数，即各类土地面积的权重系数等于污染物在各类土地上的最大累积量与在研究区所有土地上最大累积量的最大值的比值. 污染物冲刷特性用影响系数表示，以表征不同土地类型下降雨径流冲刷特性的差异. 影响降雨冲刷特性的因素较多，主要可以分为两类：一是降雨的基本参数和雨型，二是降雨区域的相关特征，包括城市下垫面类型、功能区类型和排水体制类型等，其中，下垫面条件对径流量和径流污染负荷有非常重要的影响. 本文将汇水区的土地利用类型分为透水区和不透水区两大类，分别设置透水区影响系数和不透水区影响系数. 特征面积与污染物最大累积量、土地利用性质、汇水区面积、权重系数和影响系数有关，计算公式为：

Sa=wim·Sim+wm·Sm

(3)

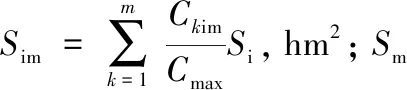
根据污染物累积-冲刷模型，降雨径流污染负荷与降雨量、汇水面积、污染物累积量、地表径流系数等因素呈正比，而特征面积表征了污染物累积特性和不同土地利用类型的冲刷特性，因此，降雨径流污染负荷与降雨量和特征面积呈正比，降雨径流污染负荷数学模型可表示为：

M=k·Sa·P+b=k1·Sim·P+k2·Sm·P+b

(4)

式中，M为污染物负荷，kg；Sa为特征面积，hm2；Sim为不透水区特征面积，hm2；Sm为透水区特征面积，hm2；P为降雨总量，mm；k为斜率，kg/(hm2·mm)；b为截距，kg.k1=k·wim，k2=k·wm.

图1 研究区各汇水区分布Fig.1 Distribution of catchments

斜率k1和k2表征降雨事件中不透水区和透水区降雨径流污染冲刷特性，其值与不透水率或径流系数有关. 特征面积与降雨量的乘积具有体积单位，可定义为“特征体积”，因此，斜率k1和k2可理解为单位体积的降雨径流污染负荷. 理论上讲，当降雨量为零时，污染量负荷为零，截距b也应该为零. 但是，受模型简化和测量误差等因素的影响，截距可能并不等于零，因此，公式(4)中增加了截距项，以提高模型的预测精度.

2 场次降雨径流污染负荷数学模型评价

2.1 材料与数据来源

2.1.1 研究区概况以安徽省某县城为例，研究区的总面积为43.6 km2，地势平缓，地面高程平均海拔26.5～33.5 m，地面自然坡降为1/9000. 研究区分为9个汇水片区，分别为ST1、ST2、ST3、ST4、ST5、ST6、ST7、ST8和ST9，各汇水片区范围见图1. 研究区的土地类型分为路面、屋面和绿地，各汇水片区的面积及其包含各土地类型的占比和面积见表1.

表1 各汇水区土地利用占比情况

2.1.2 非点源污染模型在建立场次降雨径流污染负荷数学模型时，需要多场污染负荷结果. 由于SWMM非点源污染模型易于生成不同降雨径流条件下的污染负荷样本，因此本文采用SWMM非点源污染模型的模拟结果验证模型. 以SWMM为平台，对研究区和排水系统进行概化，子汇水区690个，总面积为42.135 km2，管道876根，节点876个. 各子汇水区的不透水率和坡度利用地形资料和遥感影像借助ArcGIS计算得到. 管网计算选择动力波，下渗模型选择Horton模型，前期干旱时间选择10 d，清扫街道去除率为60%，汇水区宽度系数、不透水区糙率、透水区糙率、不透水区洼蓄量、透水区洼蓄量、最大入渗率、最小入渗率、衰减常数、晴天时间分别取0.8、0.013、0.17、1 mm、3 mm、76.2 mm/h、3.81 mm/h、2 h-1、7 d[27]. 设计暴雨雨型选择芝加哥雨型[28]，雨峰系数取0.4，设计重现期分别选取1、2、5、10、12、15和20 a(分别记为P1、P2、P5、P10、P12、P15、P20)，根据当地的暴雨强度计算公式，各降雨重现期下的降雨量分别为51、76、108、132、138、146和156 mm.

选取COD、TP和TN 3种污染物作为参考研究区降雨径流污染负荷情况的指标. 根据SWMM手册[26]和相关文献[29-30]得到污染物累积和冲刷的参数，分别见表2和表3.

表2 污染物累积参数

表3 污染物冲刷参数

2.1.3 数据来源本文中使用的两个主要数据集：(1)研究区遥感数据，是从欧洲航天局(ESA，European Space Agency)的哨兵系列卫星科研数据中心(Sentinels Scientific Data Hub)中以10 m的空间分辨率检索土地利用数据(https://scihub.copernicus.eu/dhus/#/home)；(2)研究区的地形数据，是当地人民政府提供的1∶1000 城市地形规划图.

2.2 数学模型的有效性

对7种重现期分别进行模拟，模拟时间为24 h(含退水时间). 假定有i个汇水片区，各汇水片区包含j个排水口，根据SWMM模型模拟结果即各排水口地表径流量qi,j(τ)、对应的地表径流污染物含量ci,j(τ)和模拟的总时间，积分计算出一个排水口的污染负荷，对j个排水口的污染负荷进行累积，即可得到各汇水片区污染负荷MSTi，其计算公式见公式(5). 研究区的污染负荷即所有汇水片区污染负荷的累加. 以污染物COD为例，各汇水片区在不同降雨条件下污染负荷见表4. 各汇水片区在不同降雨重现期下污染负荷与“特征体积”之间的关系分别见图2.

(5)

式中，T为模拟的总时间, s；qi,j(τ)为第i个汇水片区包含的第j个排水口对应汇水区径流量, m3/s；ci,j(τ)为第i个汇水片区包含的第j个排水口对应汇水区污染物浓度含量,mg/L.

图2 不同降雨条件下COD(a)、TP(b)和TN(c)累积总量与特征体积的关系曲线Fig.2 The relationship between cumulated COD (a), TP (b) and TN (c) and characteristic volume under different rainfall conditions

从图2中可见，降雨径流污染负荷与特征体积具有较好的线性关系，其中，TN和TP的相关系数为0.97，COD的相关系数为0.96，说明降雨径流污染负荷与“特征体积”即特征面积和降雨量的乘积呈正比，不同场次降雨下污染负荷可以用同一个公式进行描述，也从侧面说明了本文提出的估算模型是有效的. 由于各相关系数并不等于1，所以本文提出的数学模型的预测精度还需要做进一步分析.

2.3 数学模型的预测精度

研究区路面和屋面为不透水区，绿地为透水区，根据各汇水片区中各类土地面积(表1)、污染物在各类土地上的最大累积量(表2)，结合公式(3)，计算各汇水片区对应的不透水区特征面积和透水区特征面积；根据各降雨量和各汇水片区污染负荷(表4)，结合公式(4)，率定场次降雨径流污染负荷数学模型. 本文设置3种情景，即分别选择1场降雨(P5)、2场降雨(P5和P10)和3场降雨(P2、P5和P10)下的污染负荷，率定场次降雨径流污染负荷数学模型，预测其他场次降雨径流污染负荷，并与SWMM模型计算出的实际污染负荷进行对比，分析预测精度.

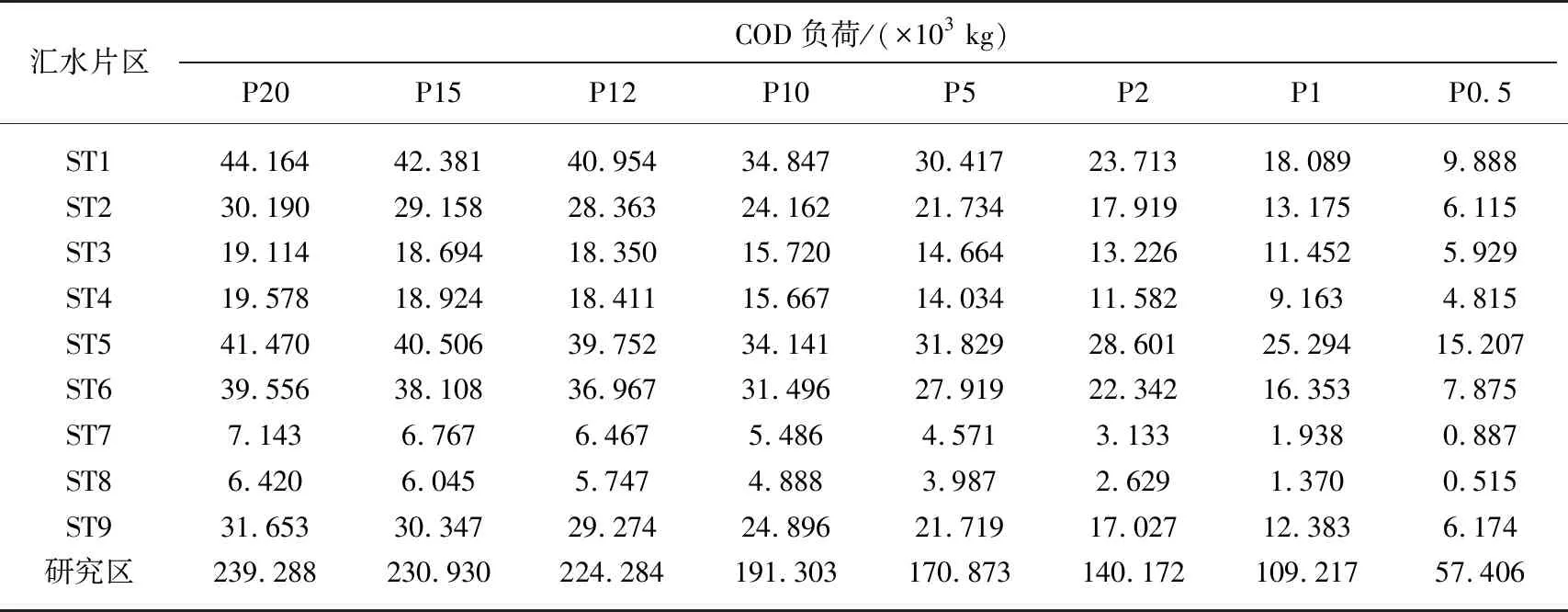
表4 各汇水片区和研究区在不同降雨条件下的COD负荷

2.3.1 各汇水片区降雨径流污染负荷预测精度以COD为例，3种情景下的率定结果见表5，各汇水片区的污染负荷预测误差如图3所示.

图3 各汇水片区污染物COD负荷预测误差(a：情景一；b：情景二；c：情景三)Fig.3 Prediction error of COD pollutant load under different storm frequencies in each catchment (a: scenario 1; b: scenario 2; c: scenario 3)

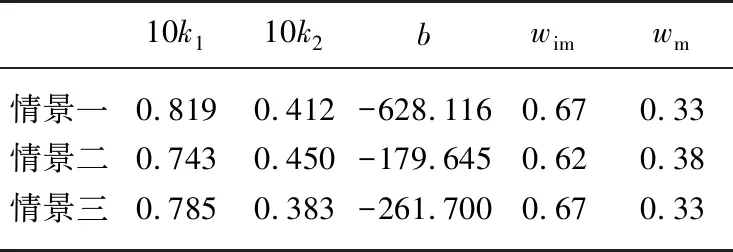
表5 模型系数和影响系数计算结果

从表5中可以看出，不透水区影响系数几乎是透水区影响系数的两倍. 透水区不仅能减少地表径流，也可控制降雨径流污染，低影响开发技术即是利用透水路面、植物透水砖、生物滞留池等技术增加透水区面积，降低降雨径流污染负荷. 影响系数的差异也表明本文提出的“特征面积”的合理性，反映了汇水区上污染物累积特性和不透水率差异引起的地表径流冲刷特性的差异.

从图3可以看出，3种情景下，P1和P2的降雨径流污染负荷的预测误差较大，P2以上的预测误差相对较小，预测精度较高.

图4 3种情景下各污染物在不同重现期下的预测误差Fig.4 Prediction error of each pollutant load under the three scenarios and different storm frequencies

2.3.2 研究区降雨径流污染负荷预测精度以整个研究区为对象，对3种情景下降雨径流污染负荷进行预测精度分析，计算误差如图4所示.

从图4中可以看出，对于COD，情景一时，P1的预测误差为-28.85%,P2及以上的预测误差在-7.3%～9.8%之间；情景二时，P2及以下的误差在-18.6%～30.0%之间,P12及以上的预测误差在-1.4%～7.0%之间；情景三时，P2及以下的误差在-29.2%以内，P12及以上的预测误差在-5.0%～0.78%之间. 对于TP，情景一时，P1的预测误差为37.62%,P2的预测误差为14.02%，P10及以上的预测误差在-10.10%～-1.82%之间；情景二时，P1的预测误差为36.02%,P2的预测误差为13.7%，P12及以上的预测误差在-9.6%～-9.2%之间；情景三时，P1的预测误差为26.61%,P12及以上的预测误差约为-11%. 对于TN，预测误差均在±11%以内.

综上，本文提出场次降雨径流污染负荷数学模型，对于P2以上的降雨径流污染负荷预测精度较高，其相对误差小于±11%，此外，降雨场次对数学模型的预测精度影响不大. 模型中有3个系数需要率定，因此，利用3场以上场次污染负荷结果便可预测其他场次的污染负荷，从而大大减小获取污染负荷数据的工作量. 对于2 a一遇以下的降雨情况，模型预测精度相对较低，其主要原因是：小降雨情况下，下垫面的洼蓄量和雨水下渗量在总降雨量中占比相对较大，采用大降雨事件的污染负荷结果率定模型参数与小降雨事件下有一定的差异，使得计算误差相对较大. 因此，对于小降雨工况而言，可以采用降雨量相近的数据进行率定，以提高模型的预测精度.

2.4 数学模型的适用性

选择武汉市和苏州市两个地区的实际案例进行分析和说明.

1)案例一

潘璐[31]研究了武汉市典型校区的降雨径流污染负荷. 研究区坡度在0.13%～0.50%之间. 经现场采样，TN和CODMn为主要污染物. 地面分为路面、屋面、庭院/广场、操场和绿地，CODMn在对应土地类别上的最大累积量分别为80、60、45、45和30 kg/hm2；TN在对应土地类别上的最大累积量分别为6、4、6、6和10 kg/hm2. 采用芝加哥雨型，雨峰系数0.4，降雨历时120 min，干旱时间10 d. 研究区降雨总量和各降雨条件下的污染负荷等基础信息如表6所示.

表6 武汉市典型校区降雨径流污染负荷[31]

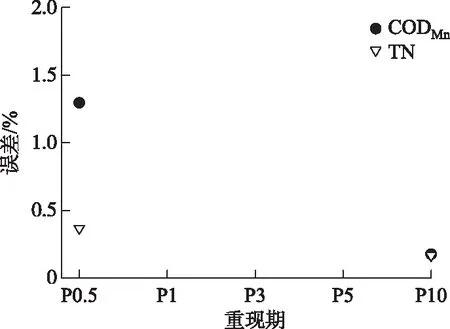
图5 案例一中CODMn和TN污染负荷总量预测误差Fig.5 Prediction error of total CODMn and TN pollution load of case 1

由于数据数量相对较少，因此，根据P1、P3、P5 3场降雨条件下的污染负荷结果率定模型，预测P0.5和P10下的污染负荷，预测精度均在98.5%以内，精度较高，计算误差见图5.

2)案例二

祁继英[32]研究了苏州市南园水系排水区的降雨径流污染负荷. 主要污染物为COD、TN和TP，地面分为屋面、绿地和交通道路. 各污染物在对应土地类别上的最大累积量见表2. 采用芝加哥雨型，雨峰系数为0.367，降雨历时60 min，干旱时间10 d. 研究区降雨总量和各降雨条件下的污染负荷总量等基础信息见表7.

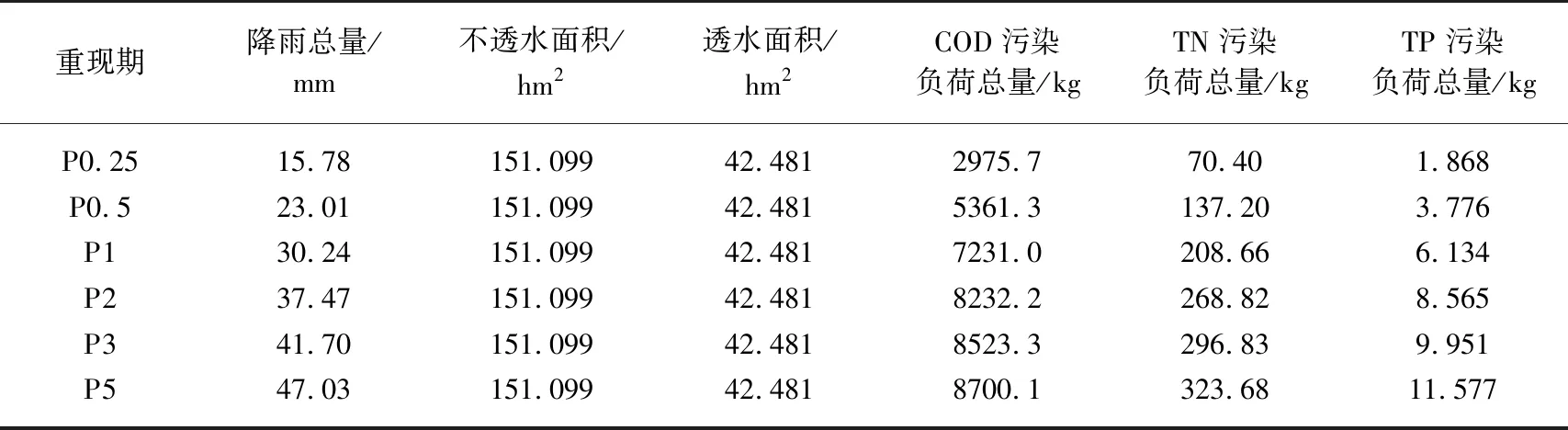
表7 苏州南园水系降雨径流污染负荷[32]

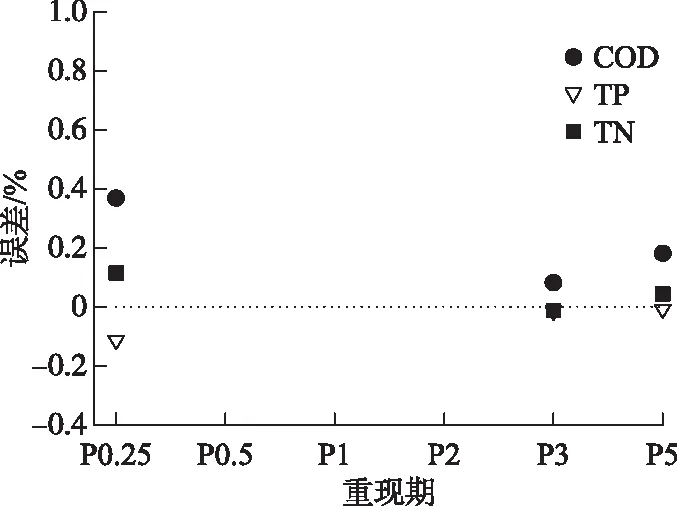
图6 案例二中COD、TN和TP污染负荷总量预测误差Fig.6 Prediction error of total COD and TN pollution load in case 2

根据P0.5、P1、P2 3场降雨条件下的污染负荷结果率定模型，预测P0.25、P3和P5下的污染负荷，预测精度均在99.5%以内，精度较高，计算误差见图6.

2.5 数学模型的局限性

本文构建了场次降雨径流污染负荷数学模型，预测精度较好，但其也有一定的局限性：

1)对于小降雨事件，模型预测精度比其他降雨条件相对较低. 为提高模型预测精度，建议采用降雨量相近的观测结果率定模型参数.

2)降雨间隔影响污染物在地面上的最大累积量，而不同土地上的污染物最大累积量是影响场次降雨径流污染数学模型预测精度的关键参数，该参数与土地利用性质和状况、绿化条件、交通状况以及土地裸露程度直接相关[4]，通常可在各类土地上选取有代表性的1 m2区域定时监测分析获得[33]，也可参考相关文献，或根据经验确定(如查阅SWMM手册等). 有分析表明[34]，一场典型降雨48 h后地表污染物才能恢复原状. 为此，对于连续降雨或者降雨间隔时间较短导致地面污染物在各类土地上的最大累积量发生变化，当全域最大累积量与局部最大累积量线性变化时，权重系数并不会发生较大变化，不会影响模型预测精度. 倘若发生较大变化且不是线性变化时，为了提高模型的计算精度，模型还需重新率定.