基于长短期记忆神经网络的冷水机组能耗预测

徐 麟 周传辉 胡云鹏 李冠男 方 曦

基于长短期记忆神经网络的冷水机组能耗预测

徐 麟1周传辉1胡云鹏2李冠男1方 曦1

（1.武汉科技大学 武汉 430081；2.武汉商学院 武汉 430056）

空调系统中冷水机组是主要的耗能部件，节能潜力较大。由于空调系统的末端需求的变化性，准确开展冷水机组的能耗预测能有效的为机组的优化控制提供参考。因此，引入长短期记忆神经网络（LSTM，Long Short-Term Memory）对冷水机组能耗进行预测，并结合EnergyPlus仿真模型数据和实际办公建筑数据验证LSTM能耗预测模型的预测效果。建立并优化LSTM冷水机组能耗预测模型。结果显示，相比于反向传播神经网络和多元线性回归模型，LSTM模型的计算时间有所增加，但LSTM模型的预测精度在三个模型中最高，LSTM能够更准确的预测冷水机组的能耗。

冷水机组；能耗预测；长短期记忆神经网络；时间序列

0 引言

随着空调系统在建筑中的应用越来越广泛，建筑能耗显著增长。空调系统的运行能耗在建筑总运行能耗中占较大比例，约三成以上[1]。冷水机组作为空调系统的主要耗能部件，占空调系统总能耗的40%以上[2]，其节能潜力巨大。空调系统的能耗预测作为空调节能研究的重要部分，能为未来短期的系统能耗进行预测和评估，从而指导空调系统的优化管理以达到节能的目的[3]。随着大数据时代的到来，多种基于数据挖掘的能耗预测方法被应用于能耗预测领域之中。由于数据挖掘方法可以在大量数据中发现隐含的信息，目前已成为比较流行的能耗预测方法[4-6]。

周峰等[7]运用支持向量机模型对办公建筑的空调系统能耗进行预测，通过将预测值与实际值对比找到运行不合理的现象。任律[8]运用建筑监测系统数据，结合神经网络模型实现了制冷机组的能效预测和自动诊断系统。严中俊等[9]运用某酒店的历史数据进行训练，建立了基于BP神经网络的冷水机组能效预测模型并取得了良好的预测效果。但关于空调系统中冷水机组的能耗预测研究相对较少。

神经网络预测法具有很强的非线性映射能力、很强的鲁棒性以及强大的自学习能力，在能耗预测领域同样得到了广泛的应用。高扬等[10]基于前向神经网络，精确的预测了建筑房间中的温度和热功率。Chang Yungchung[11]利用反向传播神经网络建立了水冷式冷水机组的能耗预测模型，通过冷冻水供回水温度与冷却水进水温度预测机组的能耗。这些神经网络模型都是非时序性的，即当前时刻的能耗值只与此时刻的输入变量有关而与变量的历史值无关。但是特定功能建筑物的使用计划通常是固定的，时间信息往往反映了建筑的占用状况和设备使用状况[12,13]。数据的时序性往往对建筑能耗和冷水机组能耗有一定影响。

为了发挥神经网络在能耗预测领域的优势，同时使预测模型能够处理时序性的数据。本文引入长短期记忆神经网络（LSTM，Long Short-Term Memory）能耗预测模型对冷水机组能耗进行预测。Hochreiter S等[14]在1997年提出的LSTM模型是循环神经网络（Recurrent Neural Network, RNN）的一种特殊形式，LSTM可以学习前面时间的信息并用于当前时刻的输出。由于梯度消失问题的存在，RNN只对短期信息比较敏感。与RNN相比，LSTM增加了一个单元状态负责承载长期状态信息，弥补RNN对长期信息不敏感的缺点，使得LSTM能够自动学习过去一段时间内的数据信息。筛选无用信息，保留有用信息，用来进行这一时刻的预测，使得预测模型更加精准。

本文采用LSTM方法建立冷水机组能耗预测模型，并运用EnergyPlus仿真数据验证模型的预测效果。建立好LSTM模型后，进行输入变量的相关性分析。本文着重于LSTM预测模型的优化，即根据预测结果优选模型输入变量组成、滞后数、网络结构和训练次数。并将LSTM模型与反向传播神经网络模型和多元线性回归模型的预测结果对比。结果表明基于LSTM时间序列的冷水机组能耗预测模型具有较高的预测精度。

1 LSTM原理

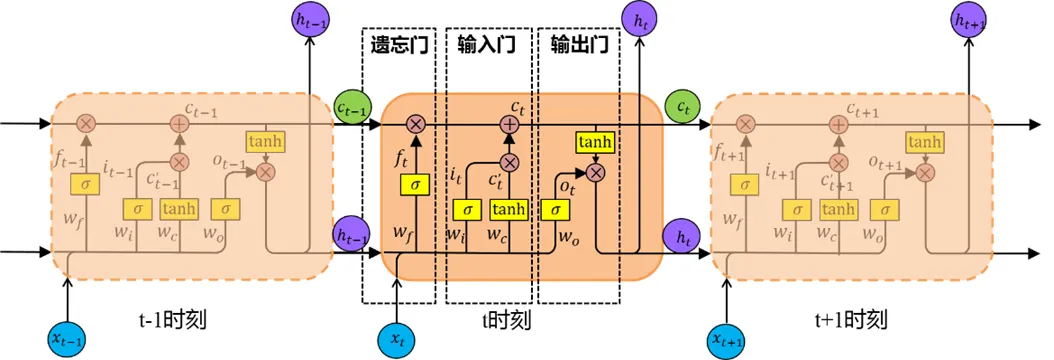
图1 LSTM结构示意图

三个门各自的作用和计算过程如下：

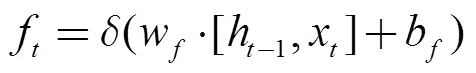
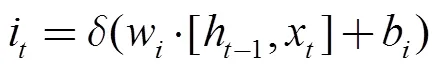
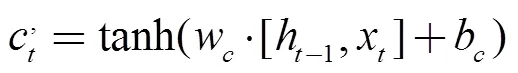
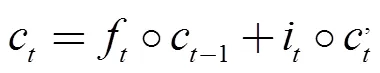
输出门：决定当前模块的输出值。

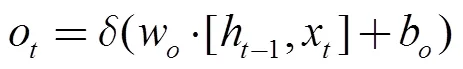
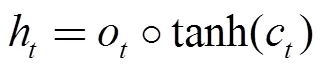
LSTM的训练计算过程采用的是反向传播算法类似的基于时间的反向传播算法（Back Propagation Trough Time，BPTT）。LSTM的训练过程主要分为四个步骤[15]：①按照公式（1）～（6）进行前向计算过程，得出每一个模块的输出值；②分别在时间和网络层级两个传播方向计算每一个模块的误差项；③根据误差项计算各个权重的梯度；④运用梯度优化算法更新权值。训练结束后，使得时间序列上的信息形成一个平衡的长短期依赖。能够运用LSTM进行冷水机组能耗预测工作。

2 数据来源和预测结果评价

2.1 数据来源

本研究采用EnergyPlus软件构建了武汉某办公大楼的空调系统仿真模型。夏季工况下，采用冷水机组和冷却塔组合的常规一次回风集中空调系统。该系统包括冷冻水循环系统、冷却水循环系统、空气处理系统。仿真输出得到正常工况下夏季制冷的完整运行数据集，输出的变量为：日期（d），时间（，h），室外干球温度（，℃），室外相对湿度（，%），太阳辐射强度（，W/m2），冷水机组能耗（Q，GJ）。数据在6月2号～8月29号之间采集。每一小时记录一组数据,共581组数据。

2.2 预测结果评价

预测结果精度评价指标采用：平均绝对误差（Mean Absolute Error, MAE）用来表示预测值和真实值之间绝对误差的平均值，均方根误差（Root Mean Square Error, RMSE）来反映预测结果和真实值之间的偏差。MAE和RMSE的值越小，预测结果的精度越高。

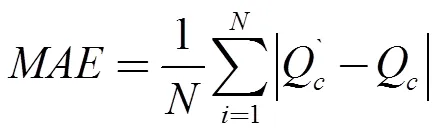
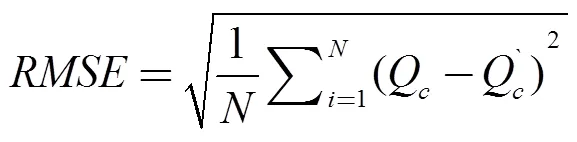
3 LSTM能耗预测模型的建立

3.1 数据处理

为去除不同变量的不同量纲和单位的影响，需要将数据进行标准化处理，以实现数据之间的可比性。采用z-score标准化方法，公式如下：

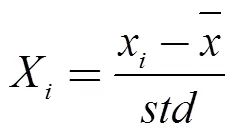
本文按照7:3的比例划分训练集和测试集，训练集为前405组（45d），测试集为后176组（20d）。

3.2 输入变量和滞后数

选取模型的输入变量分为三类：时间信息、室外气象参数和冷水机组能耗历史值（Q）。为了使能耗预测模型获得较好的预测效果，本文从三类变量中选取合适的变量组合来预测冷水机组的能耗。不同输入变量的组合方式如表1所示。

表1 不同输入变量组合

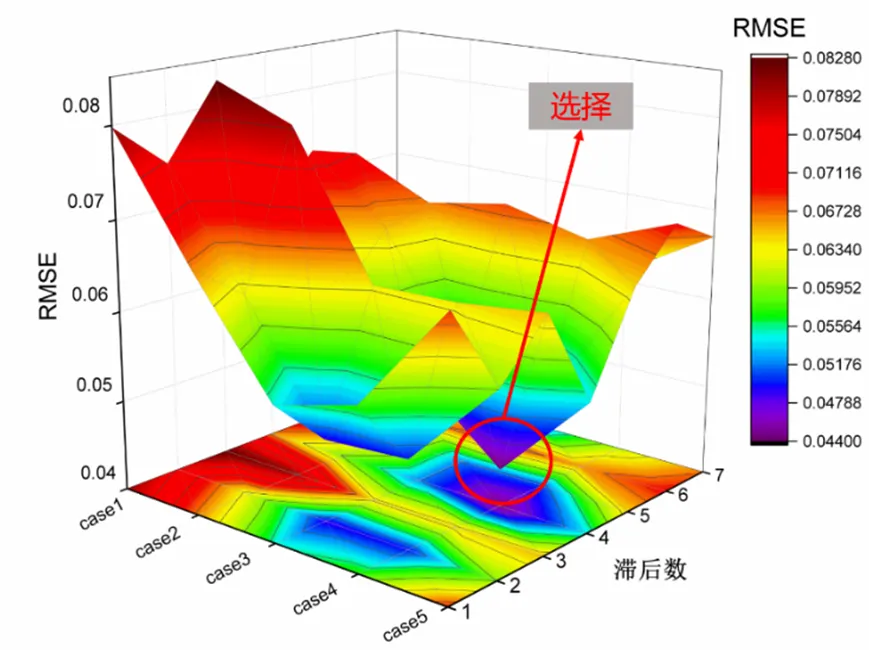
图2 不同输入变量组合和滞后数下预测结果

LSTM的滞后数是LSTM隐含层包含前后连接的同构模块的个数，即时刻数在-到范围内的时序数据参与了时刻的LSTM模型的建模。滞后数决定了当前时刻的LSTM单元中可以存储多少历史时刻的信息。滞后数的选取对LSTM模型的预测效果有着一定的影响。给定滞后数的取值范围为1～7，结合不同输入变量组合对能耗进行预测，寻找误差最小的滞后数和输入变量组合方式。如图2所示，选取预测误差最小时的输入变量组合方式4：、、、、Q，滞后数为4建立LSTM预测模型。由图2可知，输入变量加入日期后，组合5较组合4的预测效果有所降低，说明本模型中冷水机组的逐时能耗与日期的相关性不大。

3.3 网络结构

神经网络的结构往往对神经网络的性能有着较大的影响。一般来说，隐含层的层数越多，神经网络预测的精度越高，但会使网络结构更加复杂，增加计算时间。本模型选取隐含层层数的取值范围为1-4。

隐含层的神经元个数的确定没有明确的理论指导。一般以式（10）进行选取：

式中，为神经元个数；为输入节点数；为输出节点数；为取值范围1-10的常数。

本文的输入节点个数为5，输出节点个数为1，根据式（10）计算出神经元个数的取值范围为4-13。计算不同网络结构（不同神经元个数、隐含层层数）下的预测精度，选取最优的网络结构。得到的结果如图3所示，选取隐含层层数为3，神经元个数13确定神经网络结构。

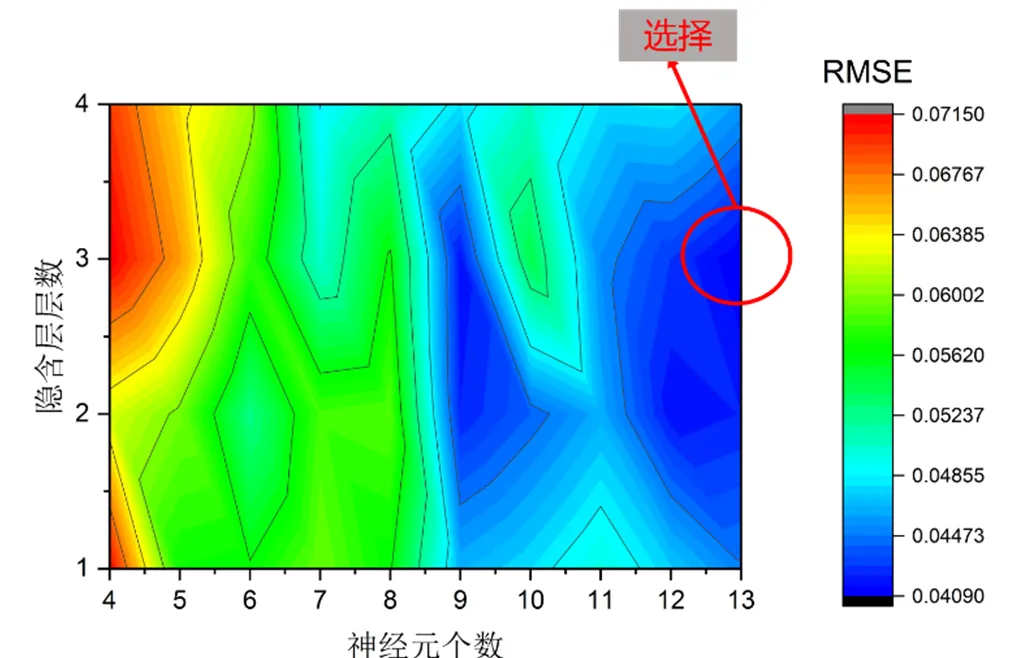
图3 不同神经元个数和隐含层层数下模型预测结果

3.4 训练次数

训练次数对LSTM的预测精度有着较大的影响。通过计算训练次数对预测精度和计算时间的影响，综合考虑以选取合适的训练次数。

由图4可知：随着训练次数的增加，模型计算的时间基本上呈线性增加的趋势。RMSE随着训练次数的增大，先逐渐降低后趋于稳定，预测精度先逐渐增大后趋于稳定。当训练次数超过150次时，模型精度虽有提高，但几乎可以忽略，反而计算时间会有一定的增加。故选定训练次数为150次。

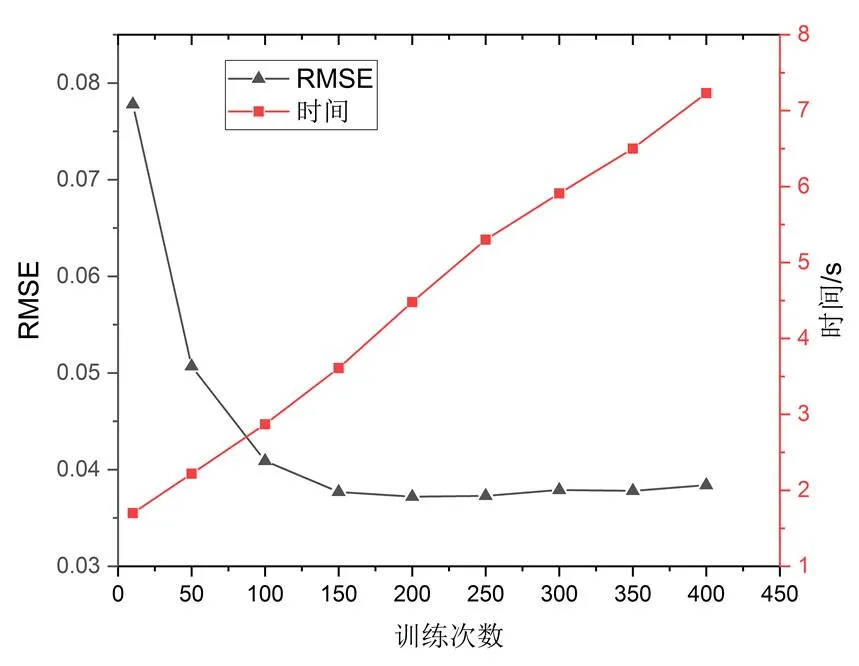
图4 训练次数对预测精度和和时间的影响

4 结果分析

综上分析，根据LSTM的预测结果对模型的参数进行优选后确定LSTM能耗预测模型。本LSTM能耗预测模型的输入变量为：时间（）、温度（）、相对湿度（）、太阳辐射（）和冷水机组历史能耗（Q），滞后数为4，神经网络隐含层层数为3层，每层所含神经元个数为13，训练次数为150次。实验所用计算机配置如下：CPU:英特尔酷睿i7-6700k,4.0GHz；内存32GB。

为了验证LSTM在冷水机组能耗预测中的优势，在同一实验环境中引入一种非线性的反向传播神经网络（BackPropagationNeural Networks,BPNN）模型和一种线性的多元线性回归（Multiple Linear Regression, MLR）模型。BPNN是一种按误差逆传播算法训练的多层前馈网络，具有较强的非线性映射能力。训练后的BPNN能够学习和存贮输入和输出之间的映射关系，用于预测模型的建立。MLR可以研究一个因变量依赖多个自变量的变化关系，根据数据建立能耗预测回归模型。选用相同的数据集建立BPNN和MLR能耗预测模型，对比分析LSTM、BPNN和MLR模型能耗预测的结果，如图5所示。

图5 三个模型对后20天逐时能耗值的预测结果

可以从图5看出，三个模型的能耗预测值和真实值的变化趋势基本相似，预测值和真实值总体上都比较接近，LSTM的预测值较BPNN和MLR更接近真实值。时刻63、72和81等是每一天上午冷水机组开机后所记录的第一组数据，因为机组刚开机时，房间温度较高，所需的制冷量较大，导致机组能耗较大，在图中反映为出现峰值。此时，LSTM的预测值与真实值较为接近，而BPNN、MLR的预测值和真实值相差较大。说明当能耗突然增大时，LSTM的预测能力比BPNN、MLR强。

运用3.2节中提出的预测结果评价指标对3种能耗预测模型进行评价，结果如表2所示。

表2 两种模型预测结果评价

为验证LSTM在实际建筑中的冷水机组能耗预测的效果，引入Kaggle平台上ASHRAE举办的建筑能耗预测大赛[16]所提供的实际建筑数据，从中选出五个实际建筑的运行数据集进行验算（LSTM预测模型的建模过程与第三节所述相同），结果如表3所示。

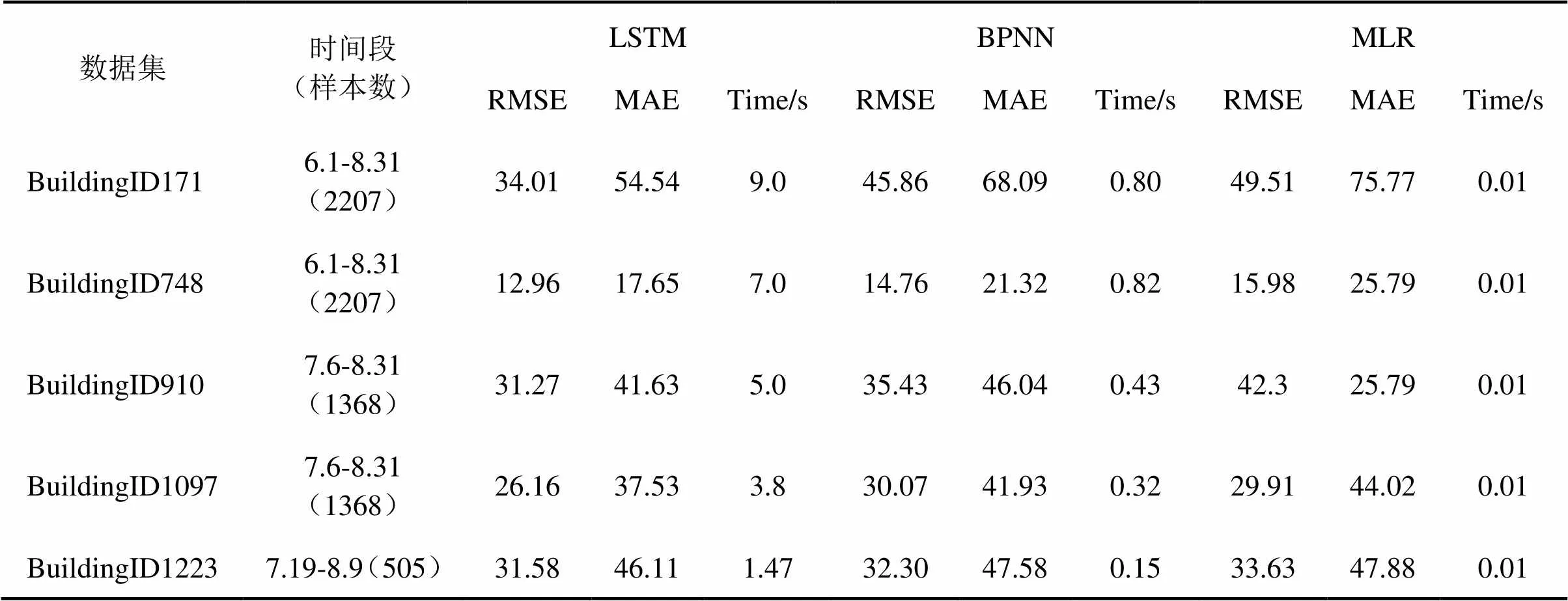
表3 实际建筑能耗预测结果

综合来看，针对模拟和实际建筑冷水机组的能耗预测。LSTM模型的预测结果的RMSE和MAE的值是三种模型中最低的，预测精度较BPNN和MLR大大提高，LSTM能够很好的预测冷水机组的能耗。LSTM模型的计算时间较BPNN、MLR有所增加，但如果计算过程在云平台上进行，计算时间能极大缩短，LSTM较BPNN、MLR多出的计算时间可忽略不计。

5 结论

本文提出了基于LSTM的冷水机组能耗预测方法，优选输入变量组成、滞后数、网络结构和训练次数后建立LSTM能耗预测模型。对模拟建筑和实际建筑中的冷水机组能耗进行预测，引入BPNN和MLR模型进行预测结果对比分析。得到以下结论：

（1）针对模拟建筑数据集，根据预测结果对LSTM能耗预测模型的参数进行优选得到：模型的输入变量为：时间（）、温度（）、相对湿度（）、太阳辐射（）和冷水机组历史能耗（Q），滞后数为4，神经网络隐含层层数为3层，每层所含神经元个数为13，训练次数为150次。这种优化模型的方法也为后续的提高模型预测精度提供思路。

（2）针对模拟建筑和五个实际建筑的冷水机组运行能耗进行预测。LSTM模型的计算时间较BPNN、MLR有所增加，但LSTM模型的预测结果的RMSE和MAE的值是三种模型中最低的，预测精度较BPNN和MLR大大提高，LSTM能够更准确的预测冷水机组的能耗。

（3）LSTM能耗预测模型相比于传统的能耗预测模型，发挥了其能兼顾时序性和非线性问题的优势，在冷水机组能耗预测中取得了更好的效果，有利于更好的支持空调系统节能工作。

致谢

感谢国家自然科学基金青年项目（51906181），湖北省高等学校优秀中青年科技创新团队项目（T201829），湖北省教育厅科学研究计划青年人才项目（Q20181110）资助。

[1] Fan C, Xiao F, Li Z, et al. Unsupervised data analytics in mining big building operational data for energy efficiency enhancement: A review[J]. Energy and Buildings, 2018,159:296-308.

[2] 胡云鹏,陈焕新,周诚,等.基于主元分析法的冷水机组传感器故障检测效率分析[J].化工学报,2012,63(S2): 85-88.

[3] 刘江岩,陈焕新,王江宇,等.基于数据挖掘算法的地铁站内温度时序预测方法[J].工程热物理学报,2018, 39(6):1316-1321.

[4] 李紫微,林波荣,陈洪钟.建筑方案能耗快速预测方法研究综述[J].暖通空调,2018,48(5):1-8.

[5] Kadir Amasyali, Nora M. El-Gohary. A review of data-driven building energy consumption prediction studies[J]. Renewable and Sustainable Energy Reviews, 2018,81(1):1192-1205.

[6] 陈焕新,孙劭波,刘江岩,等.数据挖掘技术在制冷空调行业的应用[J].暖通空调,2016,46(3):20-26.

[7] 周峰,张立茂,秦文威.基于SVM的大型公共建筑能耗预测模型与异常诊断[J].土木工程与管理学报,2017, 34(6):80-86.

[8] 任律.基于大数据的制冷机房能效自动诊断[J].制冷与空调,2019,33(5):494-496.

[9] 严中俊,闫军威.基于BP神经网络的冷水机组能效预测方法[J].制冷与空调,2013,27(5):443-446.

[10] 高扬,陈坦,胡海涛.基于神经网络的建筑节能预测方法[J].制冷与空调,2017,31(1):9-13,63.

[11] Chang Yungchung. Sequencing of chillers by estimating chiller power consumption using artificial neural networks[J]. Building and Environment, 2007,42(1): 180-188.

[12] Fan C, Xiao F, Zhao Y. A short-term building cooling load prediction method using deep learning algorithms[J]. Applied Energy, 2017,195:222-233.

[13] 杜前洲,姜梅,刚文杰,等.基于实测数据的夏热冬暖地区校园建筑负荷分析[J].制冷与空调,2019,33(2):135- 142.

[14] Hochreiter S，Schmidhuber J. Long short-term memory[M]. Supervised sequence labelling with recurrent neural networks, Berlin, Heidelberg: Springer, 1997:1735-1780.

[15] 王鑫,吴际,刘超,等.基于LSTM循环神经网络的故障时间序列预测[J].北京航空航天大学学报,2018,44(4): 772-784.

[16] ASHRAE-Great Energy Predictor Ⅲ. (2019-10-30) https://www.kaggle.com/c/ashrae-energy-prediction/overview.

Energy Consumption Prediction of Chiller Based on Long Short-Term Memory

Xu Lin1Zhou Chuanhui1Hu Yunpeng2Li Guannan1Fang Xi1

( 1.Wuhan University of science and technology, Wuhan, 430081; 2.Wuhan business school, Wuhan, 430056 )

The chiller is the main energy consuming part in the air conditioning system, which has great energy saving potential. Due to the change of terminal demand of air conditioning system, accurate prediction of energy consumption of water chiller can effectively provide reference for optimal control of the unit. Therefore, this paper introduces long short term memory (LSTM) to predict the energy consumption of water chillers, and validates the prediction effect of LSTM combined with the data of EnergyPlus simulation model and actual office building data. After the data is divided into training set and test set, the data is standardized. The energy consumption prediction model of LSTM chiller is established and optimized. The results show that compared with the back propagation neural network model and the multiple linear regression model, the calculation time of the LSTM model is increased, but the prediction accuracy of the LSTM model is the highest among the three models, and the LSTM can predict the energy consumption of the chiller more accurately.

Chiller; Energy consumption prediction; LSTM; Time series

1671-6612（2020）06-664-06

TU83

A

国家自然科学基金资助项目（编号：51906181）

徐 麟（1996.03-），男，在读硕士研究生，E-mail：1085318635@qq.com

李冠男（1988-），男，讲师，E-mail：leegna@163.com

2020-04-17