地磁矢量信息测量安装角的快速标定算法

2021-01-12高丽珍张莺莺张晓明薛羽阳

兵器装备工程学报 2020年12期

高丽珍，张莺莺，张晓明，薛羽阳

(1.中北大学电子测试技术国家重点实验室，太原 030051;2.中北大学仪器科学与动态测试教育部重点实验室，太原 030051)

制导弹药作为目前国内外实现精确打击的主要战术武器，在现代远程高精度作战中发挥着不可替代的作用[1]。制导弹药的姿态信息实时精确获取是实现外弹道飞行轨迹控制的关键核心技术，也是国内外制导武器弹载导航测姿的研究难点。利用地磁矢量信息进行弹体姿态测量技术具有自主性强、体积小、成本低、误差不累积的独特优势[2-3]，已成为制导弹药外弹道飞行中姿态测量的主要方案之一。美国、俄罗斯、法国等在本世纪初就开展了地磁测姿技术在制导弹药中应用工程化研究，并得到成功应用。受弹体安装空间限制，弹载磁矢量传感器主要是采用各向异性AMR磁阻传感器。构建基于地磁测姿系统时，由于AMR传感器体积尺寸小，焊接和弹上装配中磁敏感轴方向与弹体坐标轴方向存在度级以上的安装误差角[4-5]，且经过弹体磁干扰补偿后，地磁矢量信息的坐标基准也会发生改变，最终表现为地磁矢量信息与弹体坐标系间存在较大的安装误差角，进而导致弹体姿态角的测量精度下降。

国内对于地磁传感器的标定主要有基于高精度无磁转台的多位置标定方案和基于三维椭球拟合[6-8]的无基准标定方案两种。基于高精度无磁转台的多位置标定方案[9-10]将各轴的灵敏度、轴间耦合及安装误差角的共同作用统一表示为一个3阶误差方阵中，将三轴零偏电压表示为3维向量。该方案标定参数准确，但需要高精度无磁转台作为姿态基准，无法将安装误差角进行独立估计，且操作繁琐，不满足试验现场测试标定需求。基于三维椭球拟合的无基准标定方案[11]基本思路是基于地磁矢量传感信息在多角位置处地磁场强度不变原理，将测量矢量信息进行三维椭球拟合，再由椭球参数解算磁矢量传感器的三轴零偏电压、灵敏度、轴间耦合参数。该方案同样无法得出准确的安装误差角[12]，同时，当受弹体干扰重新标定磁测系统后，也会带来磁测信息与弹体坐标轴不平行的问题，该误差类似于安装误差角。

因此本文提出一种可应用于现场的基于牛顿迭代算法的三位置快速标定安装误差角方法。通过将弹体在无磁干扰平面中绕两个正交的轴向进行两次旋转，利用三位置的磁矢量约束关系实现三轴安装误差角的准确标定。

1 三位置磁矢量信息的非线性约束关系

标定坐标系选择标定平面的法向为y轴，平面中标定直线为x轴，z轴位于标定平面内与x、y轴构成右手坐标系，记为c系；弹体坐标系采用‘前-上-右’坐标系，记为b系。地磁矢量测量坐标系记为m系。其中m系与b系之间存在姿态失准角，记为：

α=[αxαyαz]T

其定义为弹体坐标系先绕y轴旋转αy，再绕z轴旋转αz，最后绕x轴旋转αx，如图1所示。

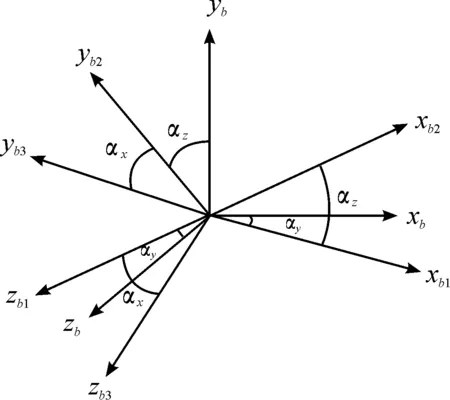
图1 地磁矢量信息失准角示意图

(1)

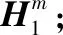
图2 旋转方案示意图

(2)

其中：

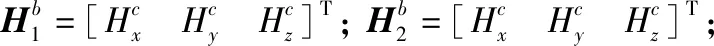
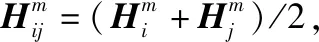
(3)

根据第2、3位置方程相加，可得：

(4)

根据第1、3位置方程相加，可得：

(5)

因此，测量磁场分量组合满足非线性约束方程组：

(6)

其中k为x、y、z轴磁场测量分量。

2 安装误差角现场快速标定算法

2.1 标定算法推导

根据三位置磁矢量信息的非线性约束关系，其中Hc与α为待求未知量，按照牛顿迭代法[13]的思想，令：

X=[αHc]

(7)

选择Xk为初值，将非线性方程组对X各分量在Xk处泰勒展开，略去其误差二次项，近似为线性方程：

ΔZ=AΔX

(8)

其中ΔZ为测量值与以迭代初值估计出来的估计值之间的估计误差；A=(∂fk,ij/Xk)为雅可比矩阵。

采用最小二乘法[14-15]，可以求出：

ΔX=(ATA)-1ATΔZ

(9)

迭代计算:

Xk+1=Xk+ΔX

(10)

直到|ΔX|小于指定的精度阈值。

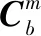
(11)

则相应的非线性方程可简化为：

(12)

初值选取为：

(13)

2.2 标定算法误差分析

设三轴磁传感器测量误差符合零均值正态分布且三轴信号相互独立，即：

(14)

其中i,j=1,2,3;k=x,y,z

因此：

(15)

当αx、αy、αz较小时，忽略二次项可得：

(16)

其中

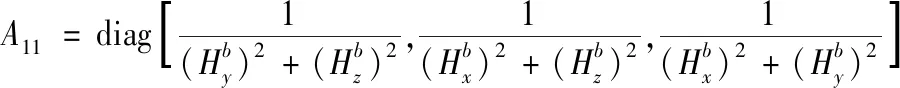
(17)

磁场信息姿态失准角的精度与磁传感测量精度和磁场矢量Hb的各分量在标定坐标系的投影有关。为使αx、αy、αz估计具有等精度，令磁场强度为|H|，则：

(18)

(19)

3 试验验证及分析

3.1 计算机仿真验证

设地磁场矢量强度为|H|=60 000 nT；三轴磁传感器的安装误差角分别为：[-1°,2°,3°]、[15°,-20°,40°]；选择标定坐标系中磁场三分量分别为：[59 983,1 000,1 000]nT、[42 421,42 421,1 000]nT、[34 641,34 641,34 641]nT、[34 641, -34 641,34 641]nT，对本文所提的三位置标定算法进行仿真分析，验证算法的标定精度与性能。仿真参数如表1所示。

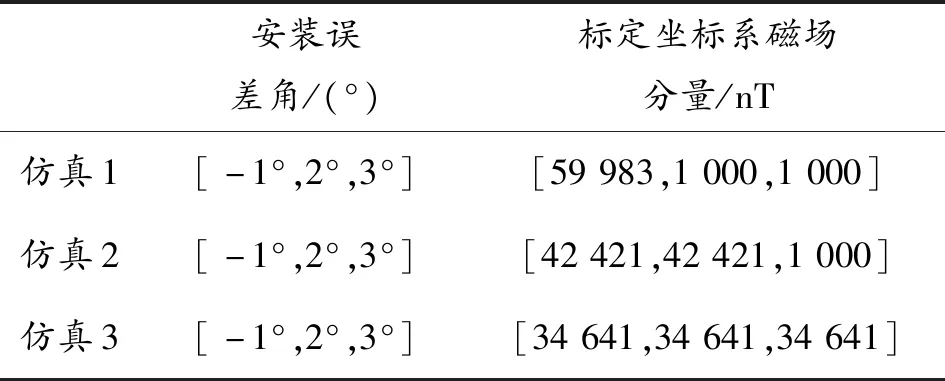
表1 仿真参数

三轴磁传感器测量误差满足零均值正态分布，标准差为100 nT。采用10 000次蒙特卡洛方法进行计算机仿真分析。仿真试验数据如表2所示。图3为10 000次蒙特卡洛统计分析安装误差角概率密度曲线图。

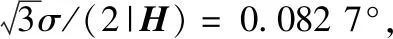
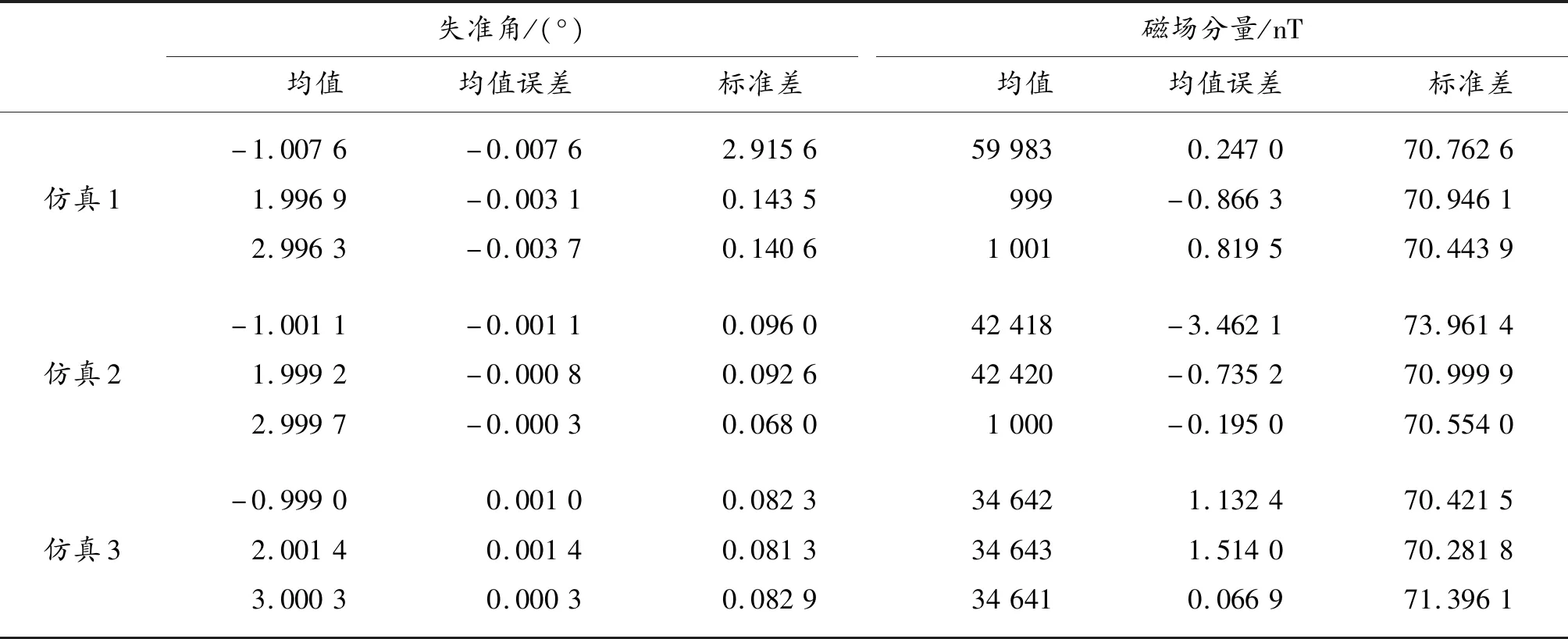
表2 蒙特卡洛仿真标定数据

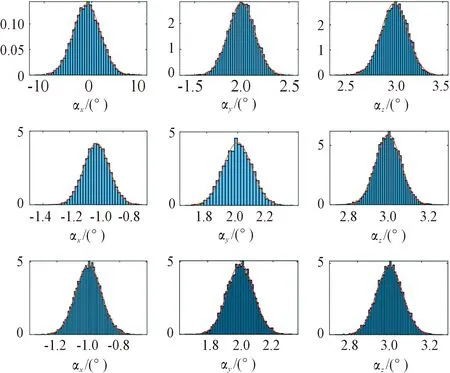
图3 10 000次蒙特卡洛统计分析安装误差角概率密度图

3.2 实测数据验证

为了进一步验证该标定算法在工程应用中对磁场矢量失准角的估计精度，将三轴磁传感器安装在某型制导弹药中，在试验靶场现场对三轴磁传感器的安装误差进行三位置标定，并对安装误差角进行弹上实时补偿，进而求取弹体俯仰角和滚转角。

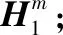
试验数据如下：标定坐标系磁场分量为[36 500,36 492,36 600]TnT。弹载三轴磁传感器的测量标准差为：86.4 nT。在位置1、2、3处的弹载磁传感器测量值如表3所示。通过本文所提的三位置标定算法，标定的三轴磁传感器安装误差角分别为：-9.271 4°、1.802 7°、 -2.484 8°；标定坐标系中地磁场三分量分别为：36 477 nT、3.655 6 nT、3.664 1 nT。