低重力模拟试验平台索并联驱动系统张力优化策略

陈强 董强 黄科 邢伟 程刚 隋毅

低重力模拟试验平台索并联驱动系统张力优化策略

陈强1董强1黄科1邢伟1程刚1隋毅2,3

（1 北京特种工程设计研究院，北京 100028）（2 北京空间机电研究所，北京 100094）（3 中国航天科技集团有限公司航天进入、减速与着陆技术实验室，北京 100094）

冗余索并联系统动力学方程的张力解不唯一，为保证随动平台在工作空间内姿态可控及索张力连续平稳，并且满足张力在最大最小限制范围，需要对其索张力优化策略进行研究。通过建立索并联驱动系统的动力学模型，分别运用封闭（Closed-Form，CF）优化法、常规最小方差优化法及将张力分为上、中、下斜拉的分类最小方差优化法对系统力控工作空间（Force Controllable Workspace，FCWS）以及典型工况的运动轨迹张力进行优化计算，结果表明：在相同张力限制条件下，采用CF优化法计算的FCWS范围最小，常规最小方差优化法次之，分类最小方差优化法计算的FCWS最大并满足系统要求；在相同运动轨迹条件下，采用CF优化法计算的张力上限最大，常规最小方差优化法次之，分类最小方差优化法的张力上限最小并满足系统要求；将分类最小方差优化法在索并联驱动系统进行张力试验，结果表明系统张力变化规律符合该优化算法的理论值，证明了该优化法的正确性。综上所述，将分类最小方差优化法确定为系统的张力优化策略。

索并联驱动系统 矢量封闭原理 索力优化 刚度控制 低重力模拟试验平台 航天返回

0 引言

实现对地外天体探测[1-3]，进行低重力模拟试验[4-5]是保证探测成功的关键环节。图1所示为我国在河北怀来县建造的采用悬吊法[6-8]地外天体低重力模拟试验平台。

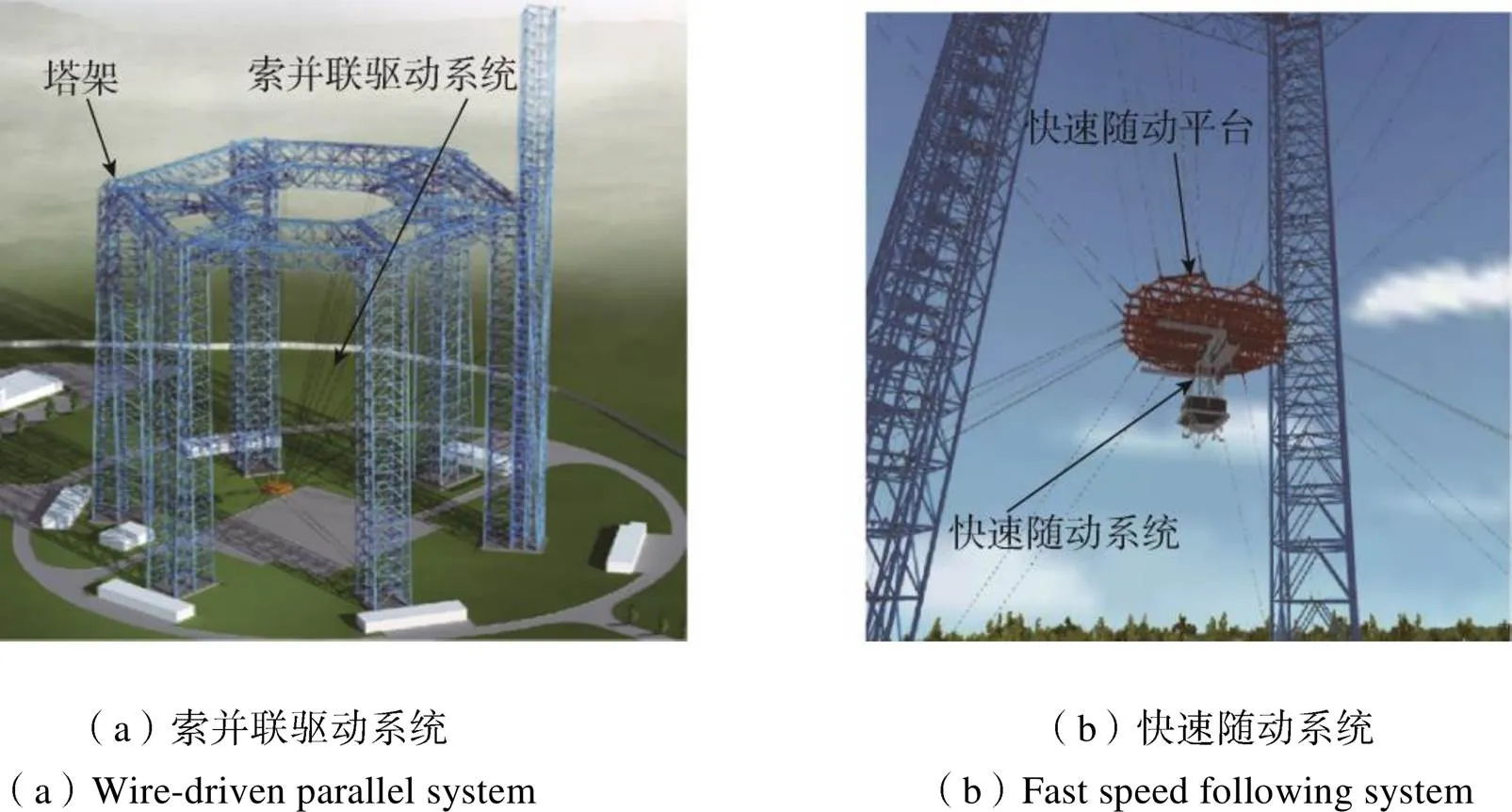
图1 地外天体低重力模拟试验平台

采用悬吊法的低重力模拟试验平台，由索并联驱动系统、快速随动系统组成。索并联驱动系统包括钢索和快速随动平台，快速随动系统安装在快速随动平台上通过吊绳连接探测器。在试验过程中，索并联驱动系统对探测器进行大范围的跟踪，快速随动系统控制吊绳保持垂直于水平面且张力恒定，抵消掉探测器的部分重力，实现对低重力环境的模拟。图1中的索并联驱动系统通过18根钢索为快速随动系统提供大范围工作空间以及高速度的运动基础，对系统随动性能有重要影响。索并联驱动系统受广义力平衡方程约束，同时绳索单向承载，为保证绳索不虚牵并且满足一定的刚度[9-11]控制要求，其张力必须要大于一定的张力下限，另一方面，绳索张力受驱动系统功率限制，必然小于一定的张力上限。同时，本系统为18索6自由度索并联驱动系统，属于冗余约束系统[12]，在工作空间中绳索张力的解并不唯一，为保证快速随动平台在工作空间内位置姿态可控，并且在系统运行过程中绳索张力连续及各绳索之间张力差异尽可能地小，需要对索张力进行优化控制。

本文通过对18索6自由度并联系统建立动力学模型，并分别运用CF优化法、常规最小方差优化法及将张力分为上、中、下斜拉的分类最小方差优化法作对系统力控工作空间（Force Controllable Workspace，FCWS）及典型轨迹张力进行优化计算，通过比较分析，确定用分类最小方差优化法作为系统的张力优化策略。

1 索并联驱动系统张力优化策略

为研究方便，以根绳索具有自由度索并联系统为研究对象，建立如图2所示坐标系。pppp为局部坐标系，坐标原点p位于快速随动圆盘几何对称中心；为全局固定坐标，坐标原点在试场地面驱动系统的对称中心，坐标轴正向垂直向上。A为第根索与塔架的连接点，B为第根索与快速随动圆盘的连接点（=1, 2, 3, …,）。

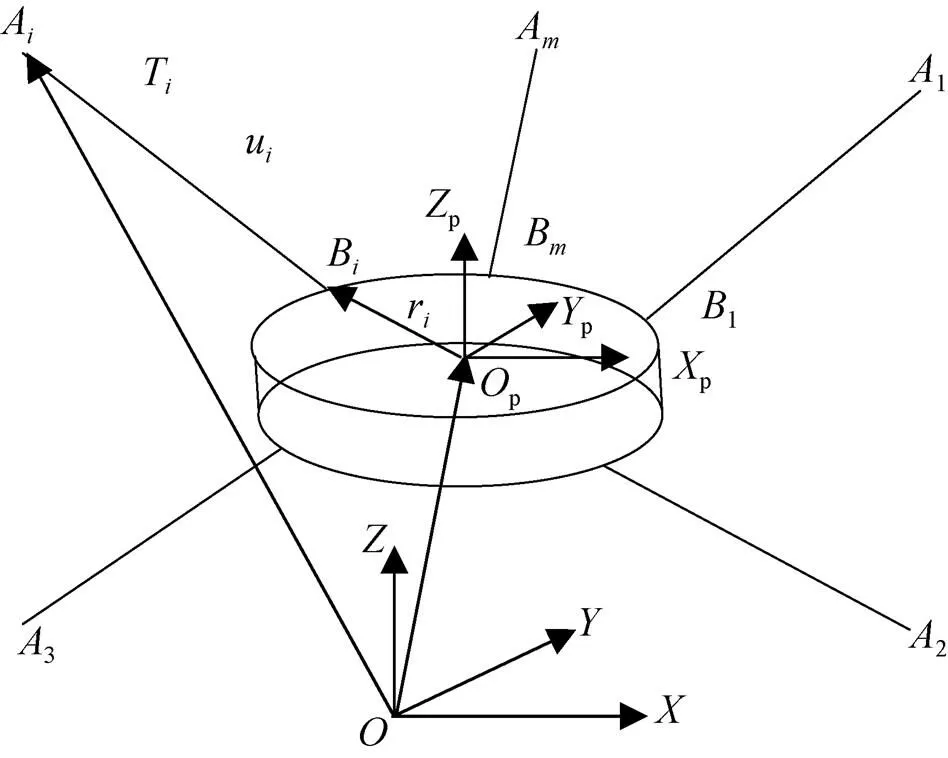
图2 系统坐标系

设=（u u u）T=（coscoscos）T为第根索张力方向在全局坐标系的单位矢量，，，分别为张力与，，轴的夹角；=（r r r）T为第根索力作用点在快速随动圆盘局部坐标系中的位置矢径；T为第根索的张力，根索组成的张力矢量=（12…T）T，则系统的广义力平衡方程为

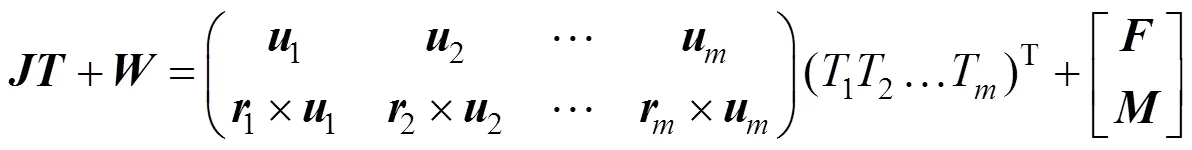
式中为与快速随动圆盘姿态和索张力方向相关的雅可比矩阵；为索并联系统的广义力，可以依据牛顿-欧拉法建立索驱动系统的6自由度动力学方程求解，包括合力和合力矩

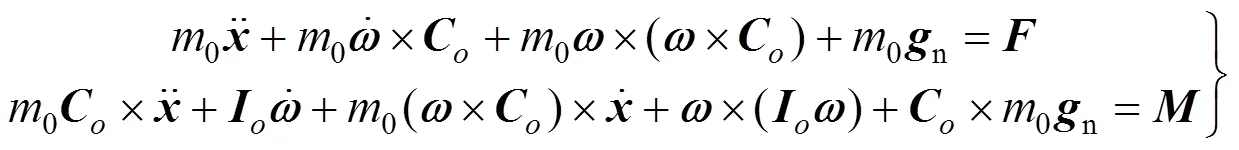
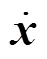
由于索并联系统只能单向受力，受驱动系统功率限制，同时为了保证绳索不虚牵，绳索张力受张力下限min与张力上限max限制，数学表达式为

min≤≤max（3）

式（1）的解为

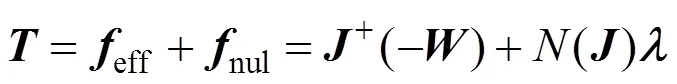
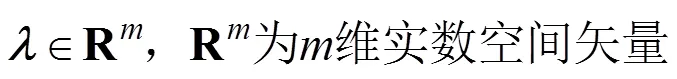
由式（4）可知，冗余索并联系统的张力解由特解及通解组成，其中通解并不唯一。为了保证系统运行的平稳，各绳索张力除了受最小、最大张力范围限制外，还要连续平稳，因此在系统工作空间内，必须对张力进行优化控制。

1.1 CF优化法

将各索张力进行拆分

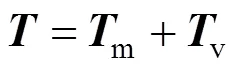
由式（5）可得

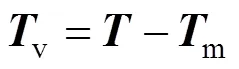
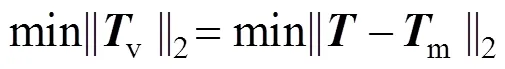
得到索力优化结果

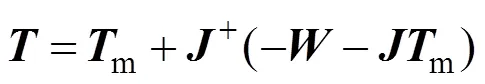
检查索力是否满足min≤≤max条件。

1.2 常规最小方差优化法

常规最小方差优化法以系统18根钢丝绳张力最小方差为目标进行优化，目的是使钢索张力在满足约束方程条件下趋向全部钢索张力的平均值，实现张力平稳连续，计算公式为

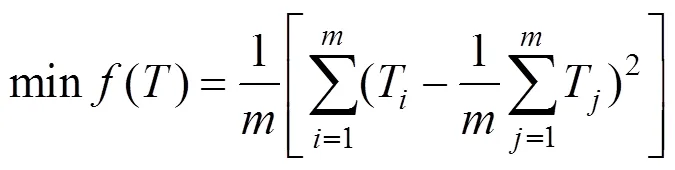
式中T，T分别为张力矢量的内外循环分量；=18。

相比CF优化法，常规最小方差优化法能够降低系统张力上限和提高张力下限，有助于扩大系统的FCWS范围。

1.3 分类最小方差优化法

分类最小方差优法是在常规最小方差优化法的基础上，将系统18根钢丝绳依据拓朴关系分为上、中、下斜拉三类，每6根钢索为一组，以各组张力最小方差为目标进行优化，计算公式为

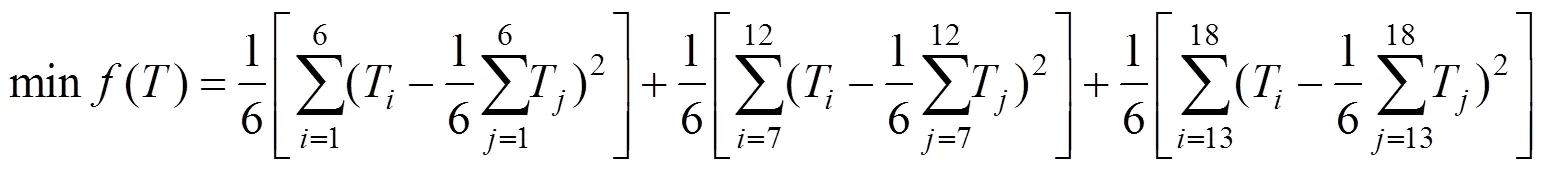
分类最小方差优化法使张力在分组内趋向其平均值，实现张力平稳连续，同时其上、中、下斜拉张力平均值相对独立，相比常规最小方差优化法，能进一步扩大其FCWS范围。

2 索并联驱动系统FCWS计算

索并联驱动系统要在工作空间内实现位置姿态可控，并满足张力限制要求，需要对其FCWS进行计算：

1）对索并联驱动预设工作空间以合理长度划分网格点；

2）提取一个网格点在-坐标系中的位姿参数，计算雅可比矩阵；

3）判断雅可比矩阵是否满秩，即rank（）=是否成立，如果不满秩，则该位姿点不属于FCWS，如果满秩，进入下一步；

5）返回步骤2），提取另一网格点重复3）~5），直到所有网格点计算完毕，即可确定系统FCWS范围。

地外天体低重力模拟试验平台18根钢丝绳在塔架上出绳滑轮位置A（坐标，为出绳点平面圆周半径）为

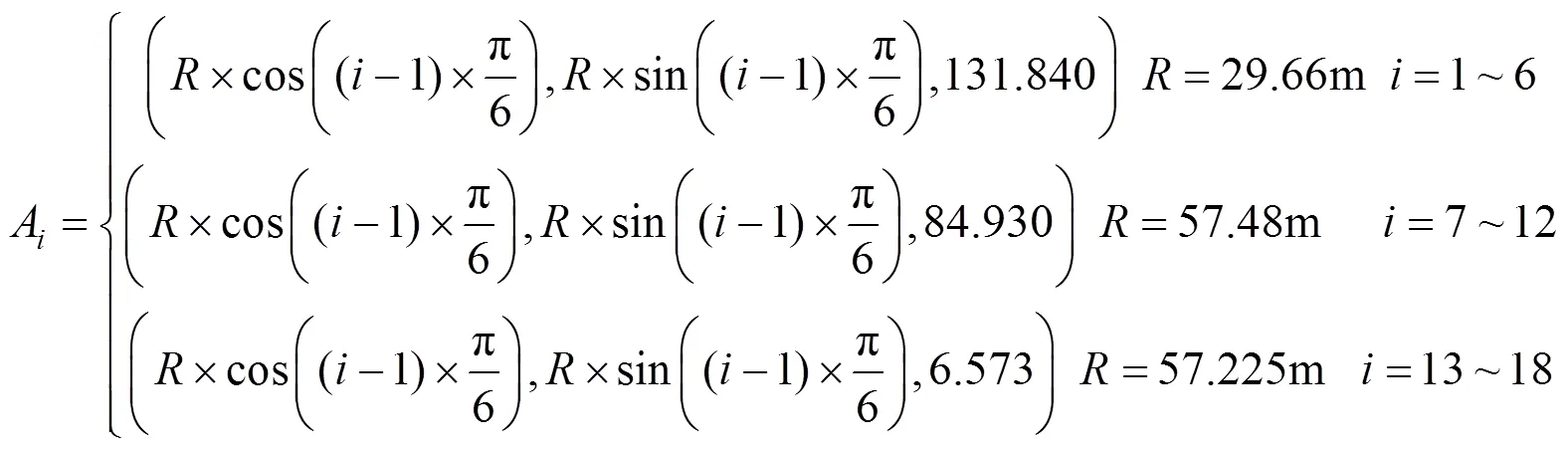
圆盘出绳点B（pppp坐标，为出绳点平面圆周半径）为

对低重力试验平台并联驱动预设的20m×20m×80m工作空间每隔1m划分网格，考虑钢丝绳切线刚度[22]所需预紧力及电机功率上限，设定索张力限制范围[min,max]=[1×104, 6×104]N，圆盘质量0=20t，分别用上述三种张力优化方法对其FCWS进行计算。

图3~图5分别为CF优化法、常规最小方差优化法、分类最小方差优化法计算的FCWS及截面示图。

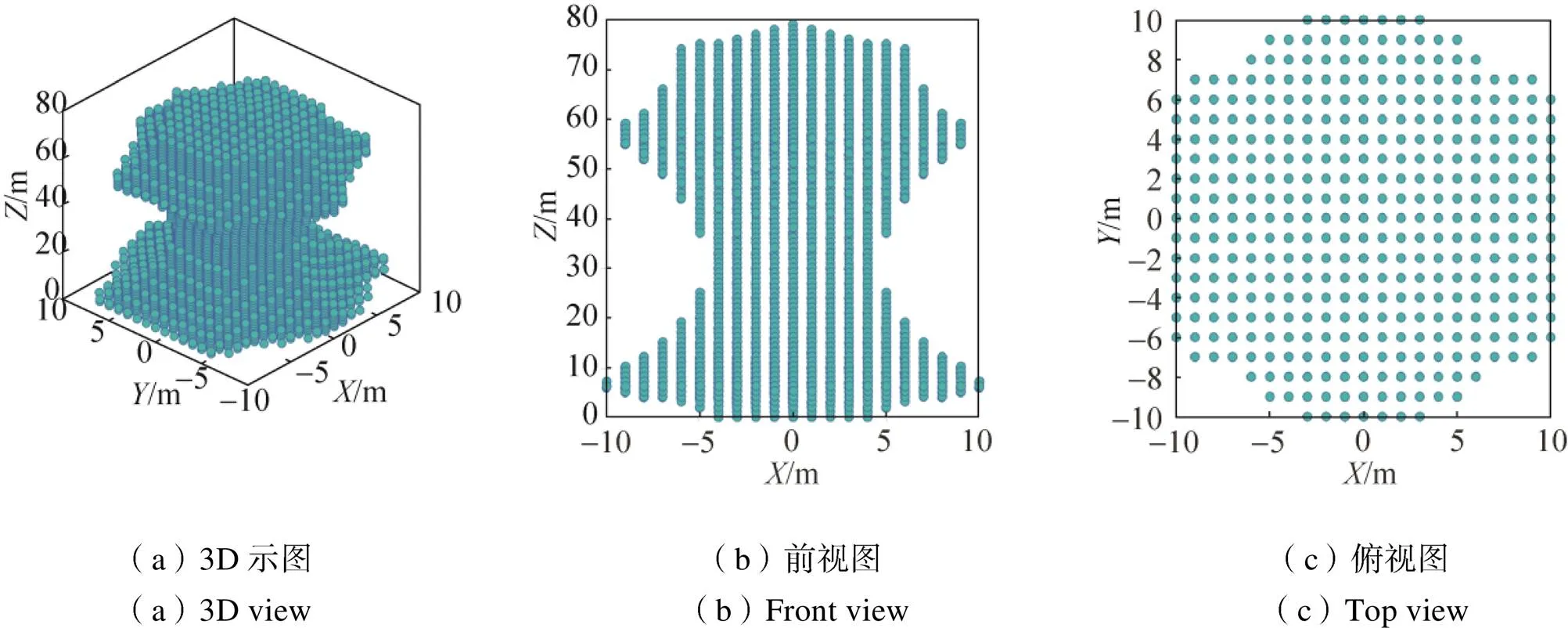
图3 CF优化法FCWS

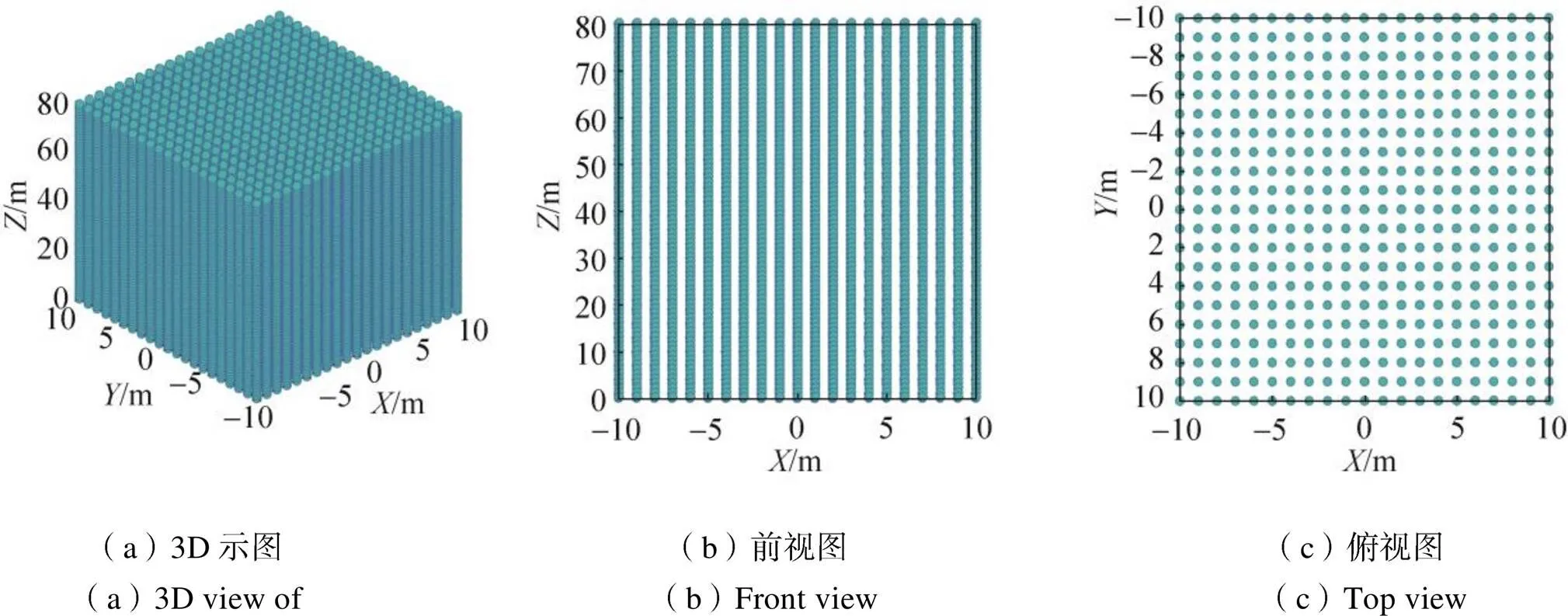
图5 分类最小方差优化法FCWS

由图3可知，采用CF优化法计算的FCWS似哑铃形状，从其前视及俯视图看，其只能在水平[-5, 5]m，垂直方向[0, 75]m范围内提供10m×10m×75m的工作空间；由图4可知，常规最小方差优化法计算的FCWS在65m高度上，水平面[–7,7]m区域内中间存在八角形空洞，只能提供20m×20m×65m工作空间；由图5可知，采用分类最小方差优化法计算的FCWS，在水平面[–10,10]m，在垂直方向[0,80]m范围内均满足张力约束条件，能提供20m×20m×80m工作空间。由此可见，在相同张力限制条件下，CF优化法计算的FCWS最小，常规最小方差优化算法次之，分类最小方差优化算法计算的FCWS最大，可以满足系统工作空间要求。

3 索并联驱动系统典型运动轨迹张力优化计算

对于索并联驱动系统在典型运动轨迹下的张力优化计算，选择工作空间内张力变化幅度最大的对角线直线运行轨迹作为计算对象：-坐标系中从（–10, –10, 0）m运行到（10, 10, 80）m，运行路径及其位移、速度、加速度曲线见图6。

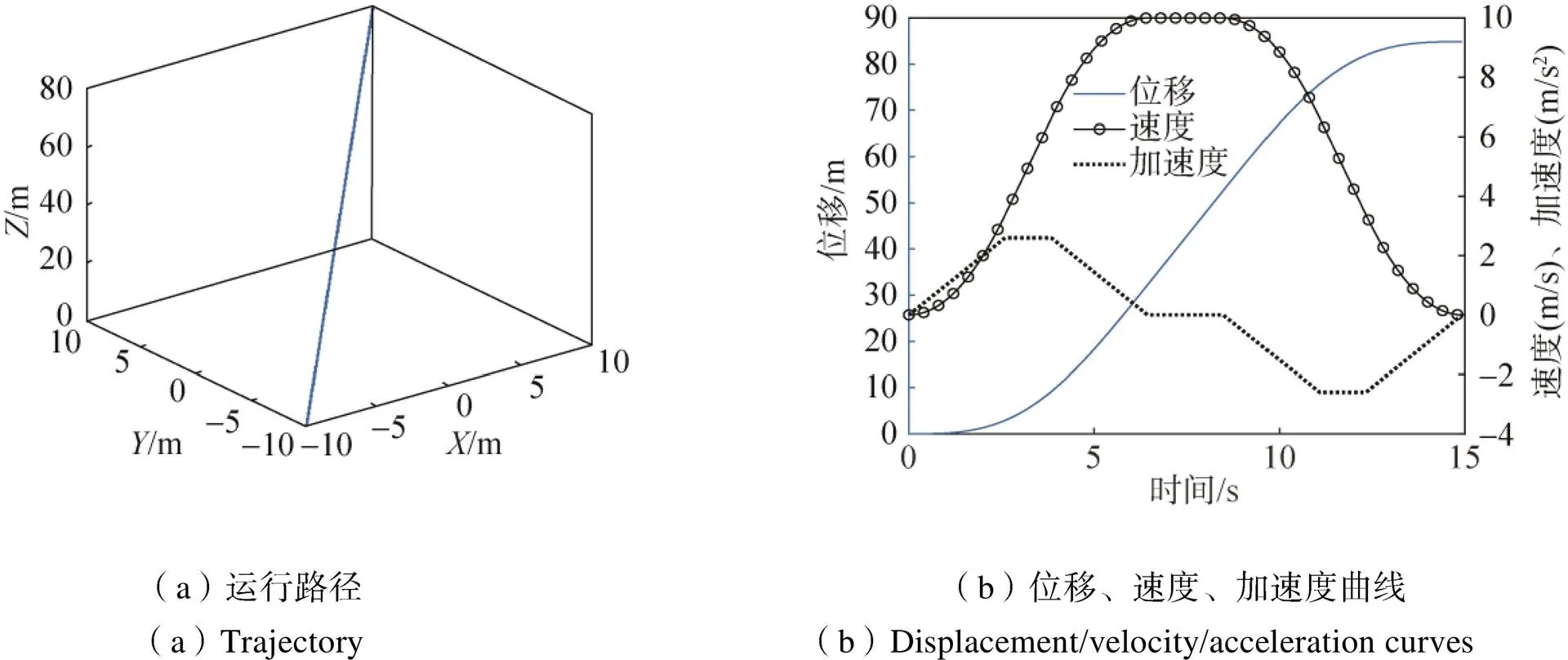
图6 典型直线轨迹

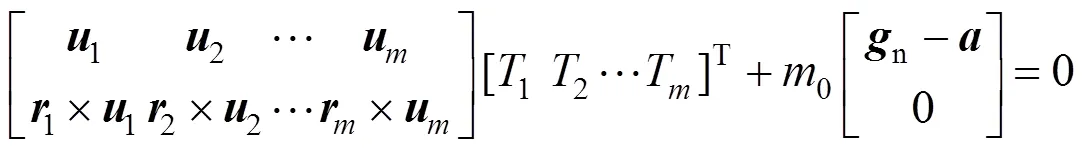
式中为平台加速度；0=20t。

分别用CF优化法、常规最小方差优化法、分类最小方差优化法三种方法，以动力学方程为约束条件，对典型运动轨迹从（–10，–10，0）m运行到（10，10，80）m的张力进行优化计算。索张力曲线见图7~图9，r1~r6为上斜拉，r7~r12为中斜拉，r13~r18为下斜拉。

由图7~9可知，在典型轨迹运行中，采用CF优化法的r8索张力最大可达7.5×104N，r5索最小张力只有5 000N左右，在运行过程中，钢索张力要么超出电机能提供的张力上限，要么过于松弛；采用常规最小方差优化法的r8索张力最大可达6.8×104N；采用分类最小方差优化法的r8索张力最大可达5.8×104N。比较可知，在相同运行轨迹条件下，CF优化法的张力上限最大，常规最小方差优化法次之，采用分类最小方差优化法计算的索张力上限最小，最小钢索张力可以维持在1×104N，满足系统对张力限制范围[1×104, 6×104]N要求。

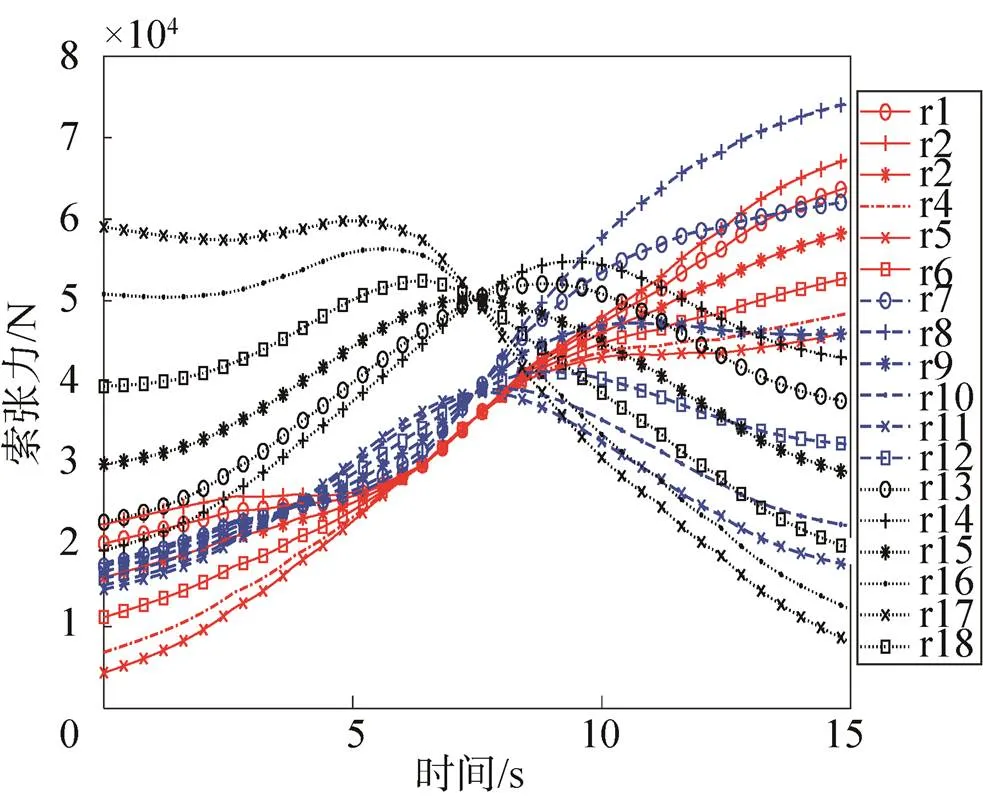
图7 CF优化法索张力曲线

图8 常规最小方差优化法索张力曲线

图9 分类最小方差优化法索张力曲线

4 分类最小方差优化法试验及结果分析

通过以上分析比较，分类最小方差优化法计算的FCWS最大，典型轨迹曲线张力上限最小，满足系统要求，下面用该方法对低重力模拟试验平台索并联驱动系统进行张力优化试验，以验证其正确性。

低重力模拟试验平台的索并联驱动系统采用伺服电机进行驱动，驱动控制器能够实时检测输出力矩，间接测量绳索的张力。控制系统采用力/位混合控制模式，首先根据典型轨迹用分类最小方差优化法事先计算好18根钢索的张力以及位置的变化曲线；在运动过程中，通过对上、中斜拉索长度按照位置变化曲线进行位置控制，使随动平台按轨迹运行；同时根据张力曲线控制下斜拉6根钢索张力大小，当张力比理论张力大时，加速释放钢索，当张力比理论张力小时，减速释放钢索。如果在运行过程中，上、中斜拉12根钢索张力变化与其理论张力曲线相符，则说明该优化算法的正确性。

图10为用分类最小方差优化法对（–10, –10, 10）m到（10, 10, 80）m直线轨迹进行张力试验结果。由结果可以看出，下斜拉索r13~r18张力按照理论曲线变化，上、中斜拉索r1~r12张力比理论值大300~800N左右，考虑传动系统的惯性力及摩擦阻力等因素，其变化趋势与理论曲线相同，说明分类最小方差优化法的正确性。

5 结论

通过建立系统动力学模型，设定索张力限制范围[min,max]=[1×104, 6×104]N，分别运用CF优化法、常规最小方差优化法及分类最小方差优化法对其FCWS及典型轨迹的索张力进行优化计算，比较分析，并对分类最小方差优化法进行试验验证，结论如下：

采用CF优化法计算的FCWS范围最小，对于典型轨迹张力最大可达7.5×104N，不能满足系统对张力限制范围的要求。

采用常规最小方差优化法计算的FCWS在65m高度上方存在空洞区域，对于典型轨迹张力最大可达6.8×104N，同样不能满足系统对张力限制范围的要求。

采用分类最小方差优化法计算的FCWS能够满足系统要求，对于典型轨迹张力最大为5.8×104N，满足系统对张力限制范围的要求。

对低重力模拟试验平台索并联驱动系统采用分类最小方差优化法进行典型轨迹运行试验，试验结果表明，索张力变化规律与理论计算张力曲线相符，证明了该优化方法的正确性。

综上所述，采用分类最小方差优化法，能够将最大张力限制在[1×104, 6×104]N以内，同时满足系统对工作空间以及运行典型轨迹两方面的要求。采用该优化法，一方面保证钢索的张紧度，提高系统的刚度及定位精度，另一方面，降低驱动系统对电机功率的要求，降低系统成本，将其选为系统索张力优化策略。

[1] 李虹琳, 李金钊. NASA 发布载人火星探索之路[J]. 中国航天, 2015(11): 19-20. LI Honglin, LI Jinzhao. NASA Announced the Road of Manned Mars Exploration Mission[J]. Aerospace China, 2015(11): 19-20. (in Chinese)

[2] 朱毅麟. 载人火星航行的先期研究[J]. 航天器工程, 2006, 15(2): 1-5. ZHU Yilin. Advance Research on Manned Mars Mission[J]. Spacecraft Engineering, 2006, 15(2): 1-5. (in Chinese)

[3] 于登云, 孙泽州, 孟林智, 等. 火星探测发展历程与未来展望[J]. 深空探测学报, 2016, 3(2): 108-113. YU Dengyun, SUN Zezhou, MENG Linzhi, et al. The Development Process and Prospects for Mars Exploration[J]. Journal of Deep Space Exploration, 2016, 3(2): 108-113. (in Chinese)

[4] 彭玉明, 李爽, 满益云, 等. 火星进入、下降与着陆技术的新进展——以“火星科学实验室”为例[J]. 航天返回与遥感, 2010, 31(4): 7-14. PENG Yuming, LI Shuang, MAN Yiyun, et al. New Progress of Mars Entry, Descent and Landing Technologies—Mars Science Laboratory Case Study[J]. Spacecraft Recovery & Remote Sensing, 2010, 31(4): 7-14. (in Chinese)

[5] 滕锐, 焦子涵, 张宇飞, 等. 火星六自由度大气进入制导方法对比分析[J]. 航天返回与遥感, 2020, 41(1): 18-27. TENG Rui, JIAO Zihan, ZHANG Yufei, et al. Analysis and Comparison of Mars Atmospheric Entry Guidance Methods in 6-DOF Model[J]. Spacecraft Recovery & Remote Sensing, 2020, 41(1): 18-27. (in Chinese)

[6] 曲健刚, 陈志刚. 悬吊式低重力模拟系统控制研究[D]. 哈尔滨: 哈尔滨工业大学, 2017. QU Jiangang, CHEN Zhigang. The Control Research of Suspended Low-gravity Simulation System[D]. Harbin: Harbin Institute of Technology, 2017. (in Chinese)

[7] 蒋银飞, 王立平. 悬吊式低重力模拟系统研究[D]. 成都: 电子科技大学, 2017. JIANG Yinfei, WANG Liping. Research on Suspended Low Gravity Simulation System[D]. Chengdu: University of Electronic Science and Technology of China, 2017. (in Chinese)

[8] 王启超，黄显林. 吊索式低重力模拟器控制系统设计[D]. 哈尔滨: 哈尔滨工业大学, 2015. WANG Qichao, HUANG Xianlin. Control System Design of the Sling Hanging Low Gravity Simulation System[D]. Harbin: Harbin Institute of Technology, 2015. (in Chinese)

[9] 杜敬利, 宝宏, 崔传贞. 基于等效模型的索牵引并联机器人的刚度分析[J]. 工程力学, 2011, 28(5): 194-199. DU Jingli, BAO Hong, CUI Chuanzhen. Stiffness Analysis of Cabel-driven Parallel Manipulators Using Equivalent Model[J]. Engineering Mechanics, 2011, 28(5): 194-199. (in Chinese)

[10] 保宏, 杜敬利, 段保岩. 大型射电望远镜悬索馈源支撑系统静刚度分析[J]. 机械工程学报, 2006, 42(7): 119-124. BAO Hong, DU Jingli, DUAN Baoyan. Analysis of Stiffness of Suspended Feed System for Large Radio Telescope[J]. Journal of Mechanical Engineering, 2006, 42(7): 119-124. (in Chinese)

[11] 刘欣, 仇原鹰, 盛英. 绳牵引并联机器人的静刚度解析[J]. 机械工程学报, 2011, 47(13): 35-43. LIU Xin, QIU Yuanying, SHENG Ying. Analysis on the Static Stiffness of Wire-driven Parallel Manipulators[J]. Journal of Mechanical Engineering, 2011, 47(13): 35-43. (in Chinese)

[12] VERHOEVEN R. Analysis of the Workspace of Tendon-based Stewart Platforms[D]. Essen: University Duisburg-Essen, 2004.

[13] VERHOEVEN R, HILLER M. Tension Distribution in Tendon-based Stewart Platforms[M]//Advances in Robot Kinematics: Theory and Applications. Dordrecht, Netherlands: Kluwer Academic Publishers, 2002: 117-224.

[14] 郑亚青. 绳牵引并联机构若干关键理论问题及其在风洞支撑系统中的应用研究[D]. 泉州: 华侨大学, 2004. ZHENG Yaqing. Research on Key Theoretical Issues of Wire-driven Parallel Kinematic Manipulators and the Application to Wind Tunnel Support Systems[D]. Quanzhou: Huaqiao University, 2004. (in Chinese)

[15] 颜玉娇, 尚伟伟. 绳索牵引并联机器人的动力学建模与控制研究[D]. 合肥: 中国科学技术大学, 2015. YAN Yujiao, SHANG Weiwei. Dynamic Modeling and Control of Cable-driven Parallel Robots[D]. Hefei: University of Science and Technology of China, 2015. (in Chinese)

[16] 苏宇, 仇原鹰, 韦慧玲. 考虑绳索质量和惯性力影响的绳牵引并联机器人动力学建模和张力优化求解[J]. 工程力学, 2016, 33(11): 231-239. (in Chinese) SU Yu, QIU Yuanying, WEI Huiling. Dynamic Modeling and Tension Optimal Distribution of Cable-driven Parallel Robots Considering Cable Mass and Inertia Force Effects[J]. Engineering Mechanics, 2016, 33(11): 231-239. (in Chinese)

[17] 欧阳波, 尚伟伟. 6自由度绳索驱动并联机器人力封闭工作空间的快速求解方法[J]. 机械工程学报, 2013, 49(15): 34-41. OU Yangbo, SHANG Weiwei. Efficient Computation Method of Force-closure Workspace for 6-DOF Cable-driven Parallel Manipulators [J]. Journal of Mechanical Engineering, 2013, 49(15): 34-41. (in Chinese)

[18] 张立勋, 宋达, 李来禄, 等. 柔索驱动并联机构工作空间算法与布局优化[J]. 哈尔滨工程大学学报, 2018, 39(12): 2017-2024. ZHANG Lixun, SONG Da, LI Lailu, et al. Workspace Algorithm and Layout Optimization of Parallel Mechanisms Driven by Flexible Cables[J]. Journal of Harbin Engineering University, 2018, 39(12): 2017-2024. (in Chinese)

[19] POTT A, BRUCKMANN T, MIKELSONS L. Closed-form Force Distribution for Parallel Wire Robots[C]//The 5thInternational Workshop on Computational Kinematics. Berlin, Germany: Springer, 2009: 25-34.

[20] 曹凌, 唐晓强, 王伟方. 基于定矢量力输出的八索并联机构索力优化及实验研究[J]. 机器人, 2015, 37(6): 641-647. CAO Ling, TANG Xiaoqiang, WANG Weifang. Tension Optimization and Experimental Research of Parallel Mechanism Driven by 8 Cables for Constant Vector Force Output[J]. Robot, 2015, 37(6): 641-647. (in Chinese)

[21] 王文杰, 梁艳阳, 蒋明. 六自由度绳牵引并联机器人力位混合运动控制[D]. 成都: 西南科技大学, 2018. WANG Wenjie, LIANG Yanyang, JIANG Ming. The Hybrid Force-position Control of Cable-driven 6-DOF Freedom Parallel Robot[D]. Chengdu: Southwest University of Science and Technology, 2018. (in Chinese)

[22] 李辉, 朱文白. 柔索牵引并联机构的静刚度分析[J]. 机械工程学报, 2010, 46(3): 8-16. LI Hui, ZHU Wenbai. Static Stiffness Analysis of Flexible-cable-driven Parallel Mechanism[J]. Journal of Mechanical Engineering, 2010, 46(3): 8-16. (in Chinese)

Tension Optimization Strategy Research of the Wire-driven Parallel System of Low Gravity Simulation Platform

CHEN Qiang1DONG Qiang1HUANG Ke1XING Wei1CHENG Gang1SUI Yi2,3

（1 Beijing Institute of Special Engineering Design and Research, Beijing 100028, China）（2 Beijing Institute of Space Mechanics & Electricity, Beijing 100094, China）（3 Laboratory of Aerospace Entry, Descent and Landing Technology, CASC, Beijing 100094, China）

The solution of the redundant wire-driven parallel system force equation is not unique, to insure the pose of platform is controllable and the wires’ tensions are smooth and contained in the lower and upper limitation, it is necessary to research the system’s tension optimization strategy. By establishing the dynamic model of the wire-driven parallel system, the closed-form (CF) optimization, the general minimum variance optimization and the up-mid-down wire tension classified minimum variance optimization is used separately to calculate the system’s force controllable workspace (FCWS) and the wires’ tensions of the typical trajectory. The calculation results show that: in the condition of the same tension constrain , the CF optimization’s FCWS is the smallest, the general minimum variance optimization’s is middle, the classified minimum variance optimization’s is the biggest and satisfies the system’s requirement; under the condition of the same typical trajectory, the closed-form optimization’s upper limit tension is the maximum, the general minimum variance optimization’s is middle, the classified minimum variance optimization’s is the lowest and satisfies the system’s requirement. The classified minimum variance optimization’s force experiment shows that the measurement force curves are consistent with the theory force curves, which proves the rationality of the optimization. Based on the above descriptions, the classified minimum variance optimization is taken as the system’s tensions optimization strategy.

wire-driven parallel system; vector close principle; tension optimization; stiffness control; low gravity simulation test platform; space recovery

TP242

A

1009-8518(2020)06-0066-11

10.3969/j.issn.1009-8518.2020.06.007

2020-05-28

国家重大科技专项工程

陈强, 董强, 黄科, 等. 低重力模拟试验平台索并联驱动系统张力优化策略[J]. 航天返回与遥感, 2020, 41(6): 66-76.

CHEN Qiang, DONG Qiang, HUANG Ke, et al. Tension Optimization Strategy Research of the Wire-driven Parallel System of Low Gravity Simulation Platform[J]. Spacecraft Recovery & Remote Sensing, 2020, 41(6): 66-76. (in Chinese)

陈强，男，1975年生，2004年获北京航空航天大学检测技术与自动化装置专业硕士学位，助理研究员。研究方向为航天机电一体化工程、特种设备设计与研究，E-mail：18511891338@163.com。

（编辑：王丽霞）