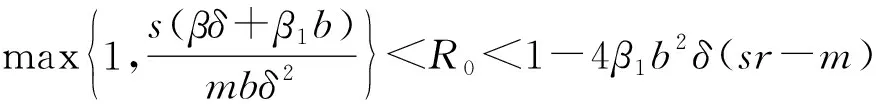具有“细胞-细胞”和“病毒-细胞”感染方式的病毒感染模型动力学分析
2021-01-11吴玉敏刘丽敏
吴玉敏,刘丽敏
(中国石油大学胜利学院 基础科学学院,山东 东营 257000)
众所周知,传染病对中国社会带来了重要的影响,几十年来,人们一直认为传染病在宿主中的传播主要是通过病毒颗粒。最早,在文献[1],[2]中,Nowak,Bonhoeffer等针对已感染细胞、健康细胞和游离病毒三者的相互作用生态关系,建立了具有“病毒-细胞”感染方式的模型,他们建立的模型较好地反应了宿主细胞与病毒之间的相互作用,故成为了常用的基本模型[3]。然而,文献[4]的研究表明,感染细胞可以通过接触方式感染健康细胞。文献[5]建立了“细胞-细胞”感染方式的HIV-1模型,并对模型的稳定性性质进行了研究,得到了保证各平衡点稳定的条件。笔者综合考虑细胞-细胞感染和病毒-细胞之间感染的两种感染方式,建立了病毒感染模型,并对模型的平衡点的稳定性进行了严格的分析。
1 模型的建立和平衡点的存在性假设
(1) 病毒感染健康的细胞之后,健康的细胞变为已感染的细胞;
(2) 已感染的细胞和健康的细胞接触,健康的细胞转变为已感染的细胞;
(3) 新的细胞以常数率产生;
(4) 未感染的细胞、已感染的细胞、病毒粒子成比例死亡。
构建病毒传播流程,如图1所示:
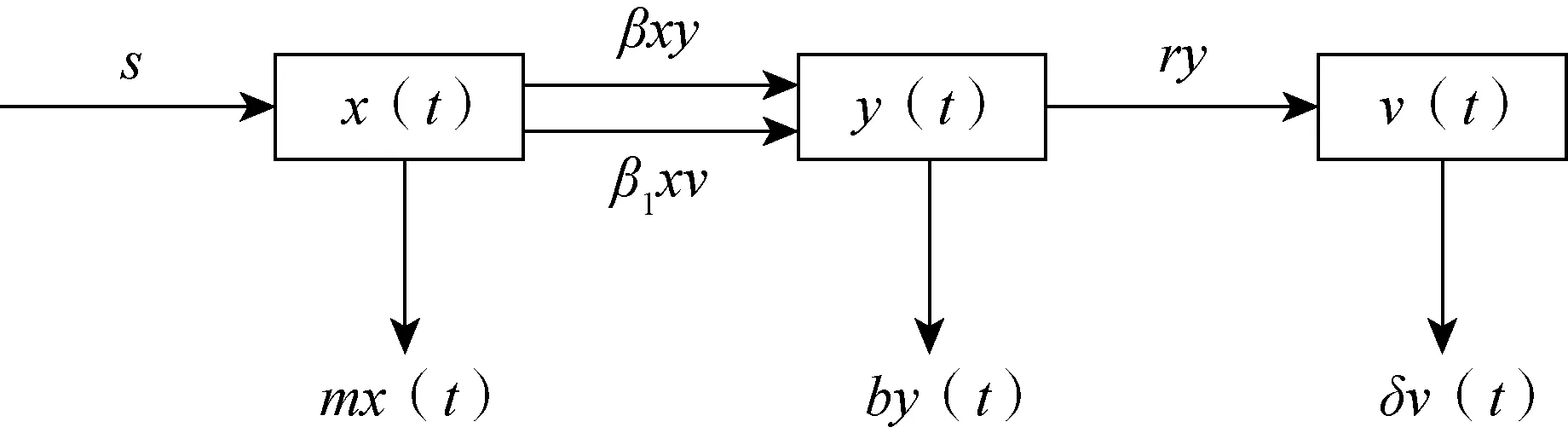
图1 病毒传播流程图
这里x(t)表示t时刻未感染的细胞的浓度,y(t)表示t时刻已感染的细胞的浓度,v(t)表示t时刻病毒离子的浓度,s,m,β,β1,b,r,δ均为常数,且大于0,s表示新的细胞的产生率,m表示健康的细胞的死亡率,β表示细胞的感染率,β1表示病毒的感染率,b表示感染细胞的死亡率,r表示死亡细胞溶解产生病毒的产生率,δ表示病毒被清除的速率。
建立下列细胞-细胞和病毒-细胞感染方式的病毒感染模型
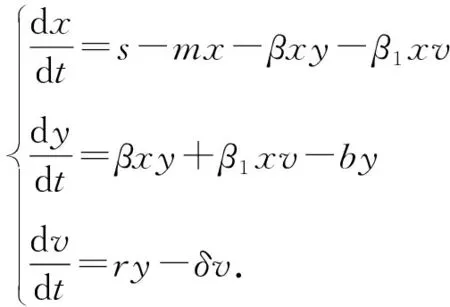
(1)
假设模型(1)满足以下初值条件
x(0)>0,y(0)≥0,v(0)≥0.
(2)
易知具有初值条件(2)的模型(1)的解是恒为正的。
定义基本再生数为
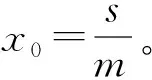
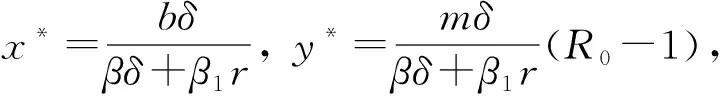
证明:根据平衡点的求解方法,解代数方程组
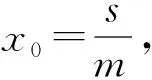
当y≠0,v≠0时,由ry-δv=0得
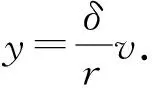
(3)
将式(3)代入βxy+β1xv-by=0得
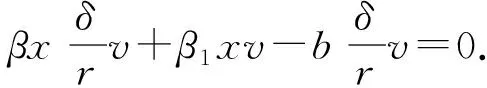
(4)
因为v≠0,所以有
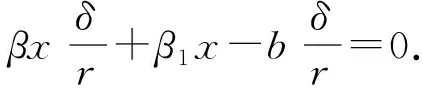
(5)
2 平衡点的稳定性
模型(1)的雅可比矩阵为
2.1 平衡点的局部稳定性
定理2当R0≤1时,E0是局部稳定的,否则是不稳定的。
证明:模型(1)在E0处的雅可比矩阵为
即
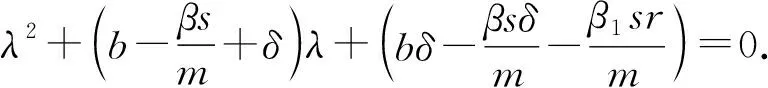
(6)
当R0≤1,即bmδ≥βsδ+β1sr时,可得
因此λ2<0,λ3<0,此时无病平衡点是局部稳定的。
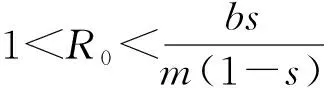
证明:模型(1)在E1处的雅可比矩阵为
则特征多项式
|λE-J(E1)|=(λ+δ)[(λ+m+βy*+β1v*)(λ+b)-(λ+m)βx*]=0
(7)
可得λ=-δ,或
λ2+Aλ+B=0
(8)
其中
A=mR0+b-βx*,B=mbR0-mβx*.
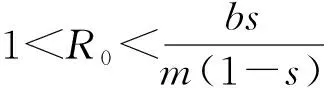
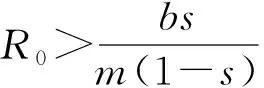
2.2 平衡点的全局稳定性
定理4 当R0≤1时,E0是全局渐近稳定的。
证明:构造Lyapunov函数
显然,对于模型(1)的正解,V(t)>0,且
故由Lasalls不变集原理可知,当R0≤1时,E0是全局渐近稳定的。
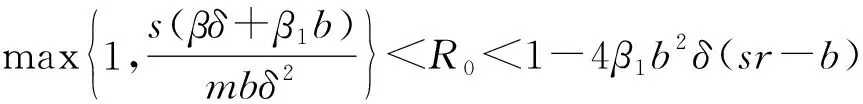
证明:构造Lyapunov函数
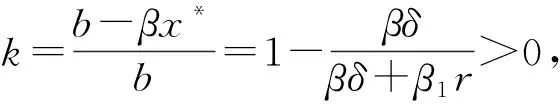
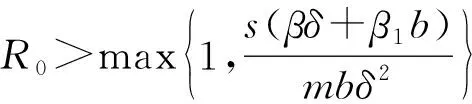
从而有
V′(t)≤(s+mx*+by*+kδv*)-(mx*+βx*y*)y0-
这里
又因为当R0<1-4β1b2δ(sr-b)时
4sδb2-(4sbβδ+4β1b2)x*+(bδ-βδx*)2v*=
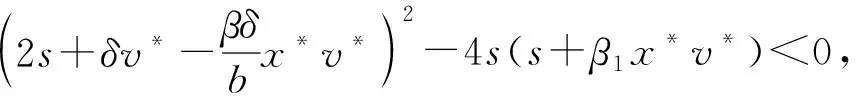
3 数值模拟
为了验证文中几个定理的正确性,考虑以下模型,进行数值模拟。
根据建立的模型(1),选取s=0.5,β=0.1,δ=0.2,β1=0.1,r=0.2,m=0.4,b=0.4,得到模型(9)
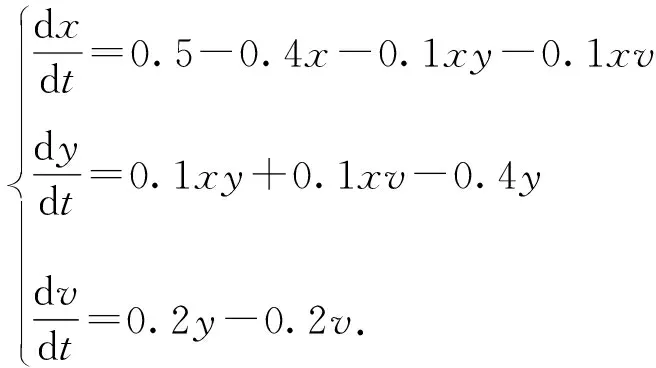
(9)
计算可知R0=0.625,于是模型(9)满足定理4的条件,所以模型(9)的无病平衡点E0是全局渐近稳定的。利用Matlab软件,进行数值模拟,得到图2,图2支持这一结论。
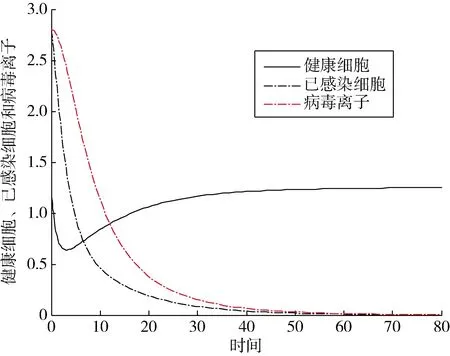
图2 模型(9)数值模拟
选取s=0.4,β=0.6,δ=0.95,β1=0.9,r=0.85,m=0.5,b=0.75,得到模型 (10)
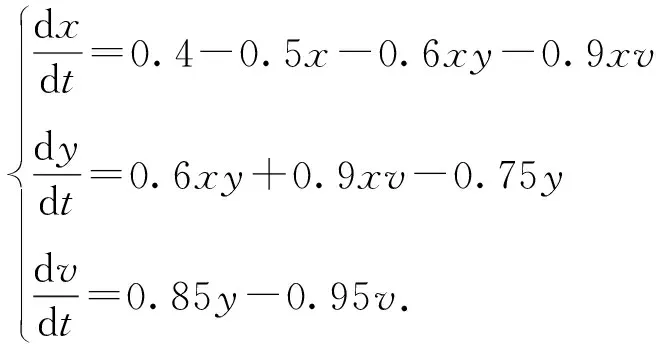
(10)
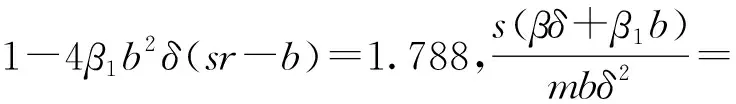
通过图2可以看出,即使初始状态有人群被感染,疾病最终也会消失。图3说明短时间内感染人数达到峰值,然后慢慢减少,最后稳定在地方病平衡点处。
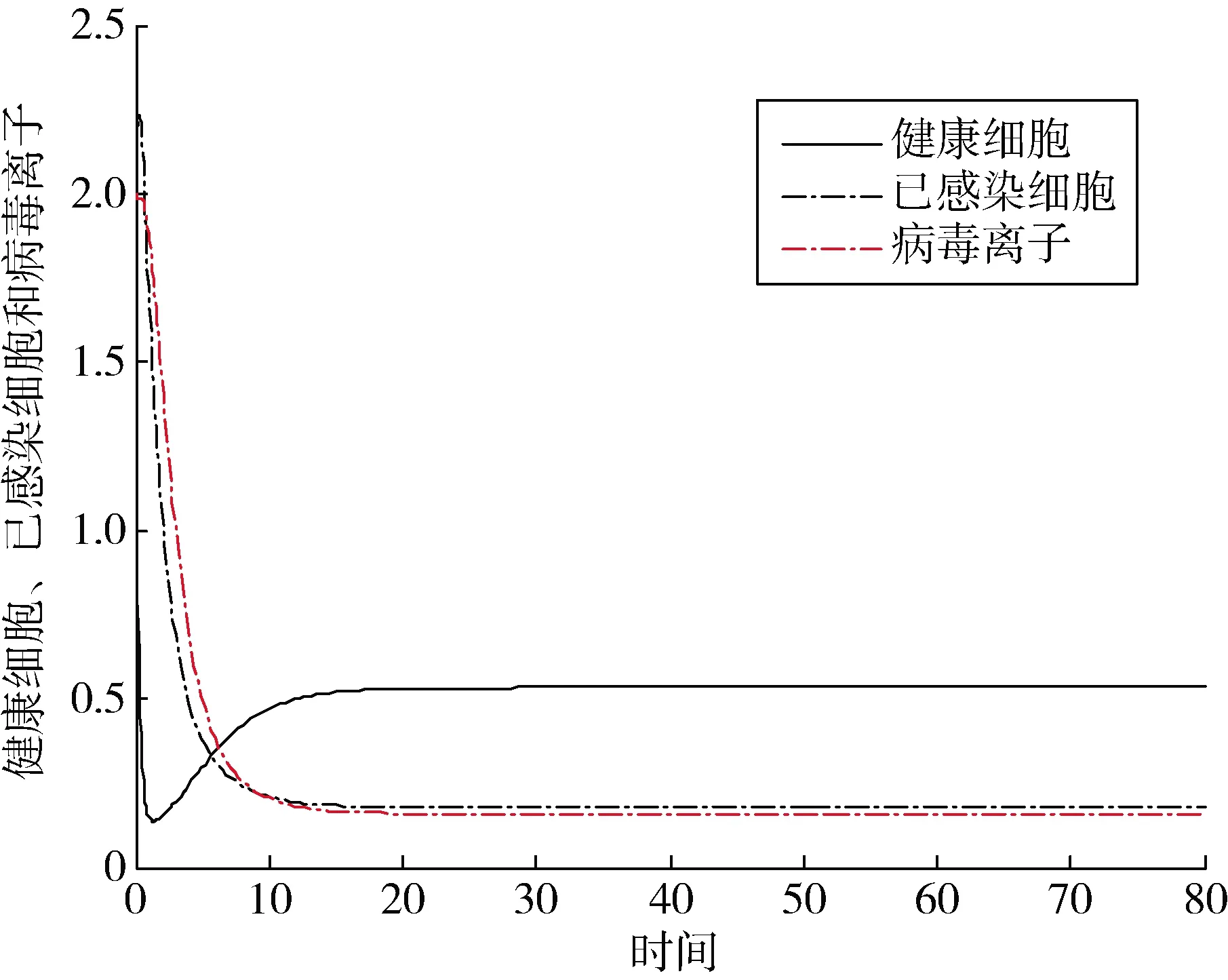
图3 模型(10)数值模拟
4 结 论
(1)利用代数的方法,计算得到了系统无病平衡点和地方病平衡点。