基于改进Q学习的“货到人”拣选系统AGV路径规划

杜卓颖，李金禧，张祥来，朱 琳

（哈尔滨商业大学 管理学院，黑龙江 哈尔滨 150000）

1 引言

目前仓储内的货物流通开始更多的使用AGV智能小车作为载体，随着自动化水平的提高和成本的降低，现在多数使用的是“货到人”拣选模式。在拣选过程中，系统内的拣选人有固定站位，货物通过AGV小车等载体自动输送到拣选人面前。这种模式不仅可以提高拣选和存储的效率，还可以有效减低人工成本和劳动强度[1]。因此，本文将在以“货到人”拣选系统为背景的仓储中进行仿真实验。

目前对单智能体的路径规划方法有很多：一是使用搜索算法,如姜涛，等[3]提出利用Dijkstra 算法提高路径规划中的定位精度问题，使机器人与障碍物之间距离最大化，使移动机器人的运动轨迹具有较高的可执行性，减少碰撞几率，实现了小型移动机器人在信号丢失情况下的自主返航；陈靖辉，等[4]基于A*算法，通过消除对称路径，减少扩展节点的方法，提高搜索效率和算法性能；二是使用启发式算法，如梁凯，等[5]基于蚁群算法进行动态路径规划时的缺陷，提出了结合狼群分配原则、局部搜索策略和两步可行域搜索策略的改进蚁群算法；周驰，等[6]在标准粒子群算法的基础上，结合遗传算法的交叉变异思想、变邻域搜索、动态惯性权重的寻优策略，对仓储环境叉车运动进行寻路。

随着对强化学习研究的深入，部分学者也将强化学习方法应用于路径规划中。由于Q学习的探索方式，导致Q学习算法的收敛速度并不高，算法性能较差。因此很多人对传统Q学习算法进行改进，如王健，等[7]改进传统Q学习算法探索收敛速度过低的问题，通过动态调整探索因子的探索方法，提高机器人对环境的熟知程度，提高算法收敛速度；张峰，等[8]提出基于树的经验存储结构来存储探索过程中的状态转移概率，并据此提出了基于期望经验回放的Q学习算法。该方法降低算法复杂度，实现对环境状态转移的无偏估计，减少Q学习算法的过估计问题；赵辰豪，等[9]使用Boltzmann 选择策略，通过动态调整算法对动作的选择概率，使回报值与动作被选概率呈正相关，提高学习的合理性与有效性，从而提高算法收敛速度。除此之外，遗传算法、模拟退火算法等对于解决单智能体的路径规划问题也有很好的效果。

传统Q学习存在收敛速度慢、寻路时容易陷入局部最优解的问题。对此，本文提出一种改进Q学习的强化学习算法。受文献[2]的启发，提出将类似模拟退火算法的动态调整选择策略因子的特性与Q学习算法相结合，动态选择下一步动作，进一步提高Q学习算法的收敛速度，提高算法性能，改善传统Q学习容易陷入局部最优的问题。仿真方面，结合“货到人”拣选系统这一实际物流场景，模拟出仓储AGV拣货送到拣选台的流程，找到了一种能够在充满货架和障碍的静态环境中使AGV 路线最优的解决方法。

2 “货到人”拣选系统

“货到人”拣选采用物流机器人（AGV）驼载货物到拣选人面前的方式，供人拣选。相对于传统的“人到货”拣选方式，“货到人”拣选在作业效率、成本控制、拣选正确率等方面，都具有显著的优势[10]。目前有几种主流的“货到人”拣选方案，包括多层穿梭车方案、Autostore 方案、Miniload 方案、旋转货架方案和类Kiva 方案。从市场热度来看，随着亚马逊Kiva 机器人的大规模应用，类Kiva机器人（也称为智能仓储机器人）得到越来越多的关注和追捧[11]。该系统相较于其他的方案更加灵活，易扩展性强，高度自动化，可以极大程度地代替人工。同时项目建立交付快，非常适用于一些库存保有量大、商品订单多品种的场景。本文采用的便是类Kiva机器人方案。

3 基于Q 学习的AGV路径规划

强化学习是做出最佳决策的科学，Q学习算法是其中的一个分支。Q学习算法是马尔科夫决策过程的递增式动态规划算法，由状态、动作和奖励组成的三元组来对Q值进行选择更新，最终得到AGV 最大限度的回报值，是通过值函数进行估计后验概率来得到预测的算法。在进行路径规划时，Q学习算法对AGV进行初始化操作，设AGV的初始状态为s,并建立矩阵R和矩阵Q分别存储AGV 每步探索的即时奖励和Q值函数值。通过AGV随机选择下一步路径动作a 并计算相应的Q值函数值，来进行Q值表的更新操作。在该算法下，每个Q(s,a)都有对应的一个Q值，即为得到的累计回报。最终根据得到的最大累计回报，选择相对应的AGV行走动作。

传统Q学习的主要流程如图1所示。

对于Q学习来说，最重要的一步是根据Q值函数对Q值表进行更新。Q值函数一般表示为：

根据Q值函数计算AGV路径下一步动作所带来的可能影响，并根据选择策略选择带来最好影响的路径动作。其选择策略为：

距离计算采用曼哈顿距离测算法，AGV 小车只能上下左右运动,排除对角线行走：

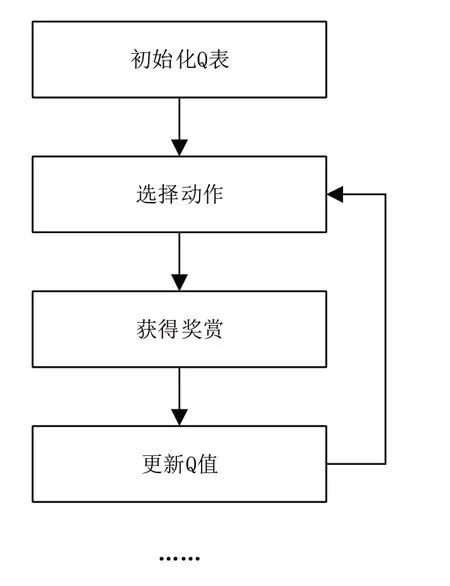
图1 传统Q 学习流程

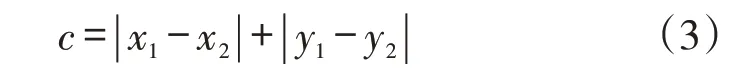
其中，Q'为更新的Q值函数值，s'为s的下一时刻路径状态，α'为α的下一时刻路径动作。α为学习率，定义了Q值更新占原Q值的比例，γ为折扣因子，定义未来奖励的重要程度。α和γ是Q值函数的两个可操作数，通常认为取值0时为程度最不重要，取值1时为程度最重要。

但传统Q学习算法具有自身的局限性，在寻路时较容易陷入局部最优解，并且当仓储内的AGV 数量增多或者单一AGV 可选择的行走动作集合过大时，易导致整体的状态空间过大，出现Q学习算法效率降低，学习效果不明显等问题，产生“维数灾难”。

4 基于改进Q 学习的AGV路径规划

4.1 模拟退火算法

模拟退火算法从某一较高初始温度出发，通过温度参数的不断降温，使算法中的解逐步趋于稳定。并在解集中以一定的概率跳出局部最优解，来寻找目标函数的全局最优解。在模拟退火算法执行过程中，主要存在三个参数设定问题：温度T、退火速度（迭代次数L）和温度管理（降温方式）。

每求出一个新的最短路径解x'，都要计算优化目标函数f(x)的增量，Δf=f(x')-f(x)。在寻找最短路径时，若Δf ＜0 则接受x'作为最优路径保留下来，否则以概率p的可能来接受x作为最优路径。其中p为：

文献[2]提出，降火过程中降火函数的选取在一定程度上也会对算法收敛速度有很大的影响。经过大量文献分析，笔者发现在寻最短路径过程中对于同一温度下的可选路径进行“充分”搜索是相当必要的，而因此也消耗了大量的时间成本。循环次数增加必定带来计算开销的增大。针对此问题并且结合本算例的特殊性，笔者提出使用路径表来缓解时间成本的压力。

4.2 改进Q 学习算法

在模拟退火算法中，通过以一定的概率跳出当前局部最优解的思想对于AGV寻路优化有一定的借鉴意义。结合上述模拟退火算法的思想，对传统Q学习的每个状态和动作的选择执行模拟退火降温过程，并将其中动作选择策略添加一个概率，使得算法能够以一定的概率跳出局部最优解。根据“货到人”拣选系统的特殊性，在动态调节因子的基础上增加一个路径表PTable，用于存放已得到的最优路径，包括路径起点、路径终点、路径经过节点、该段路起点和终点四周的四个点的坐标信息，以及所存储节点之间的父子节点关系。该改进Q学习算法核心算法的伪代码如下，其流程图如图2所示。

（0）扫描路径表PTable，若起点终点存在，则直接使用；若不存在，则从（1）执行。

（1）初始化初始温度T、终止温度Tmin、退火速度q、初始化Q(s,a)。

（2）初始化动作a，状态s。

（3）退火T=q*T。

（4）AGV在状态s时刻，选择随机动作a，计算回报值amax。

（5）随机产生一个（0,1）之间的随机数β。

（6）判断β与概率p进行比较，根据上述选择策略采取相应的最好动作amax或者随机动作a。

（7）若冷却完成，T=Tmin，执行下一步；否则返回（2）。

（8）依据Q学习算法Q值函数（式（1））和选择策略（式（2））更新Q值表。

（9）更新路径表PTable。

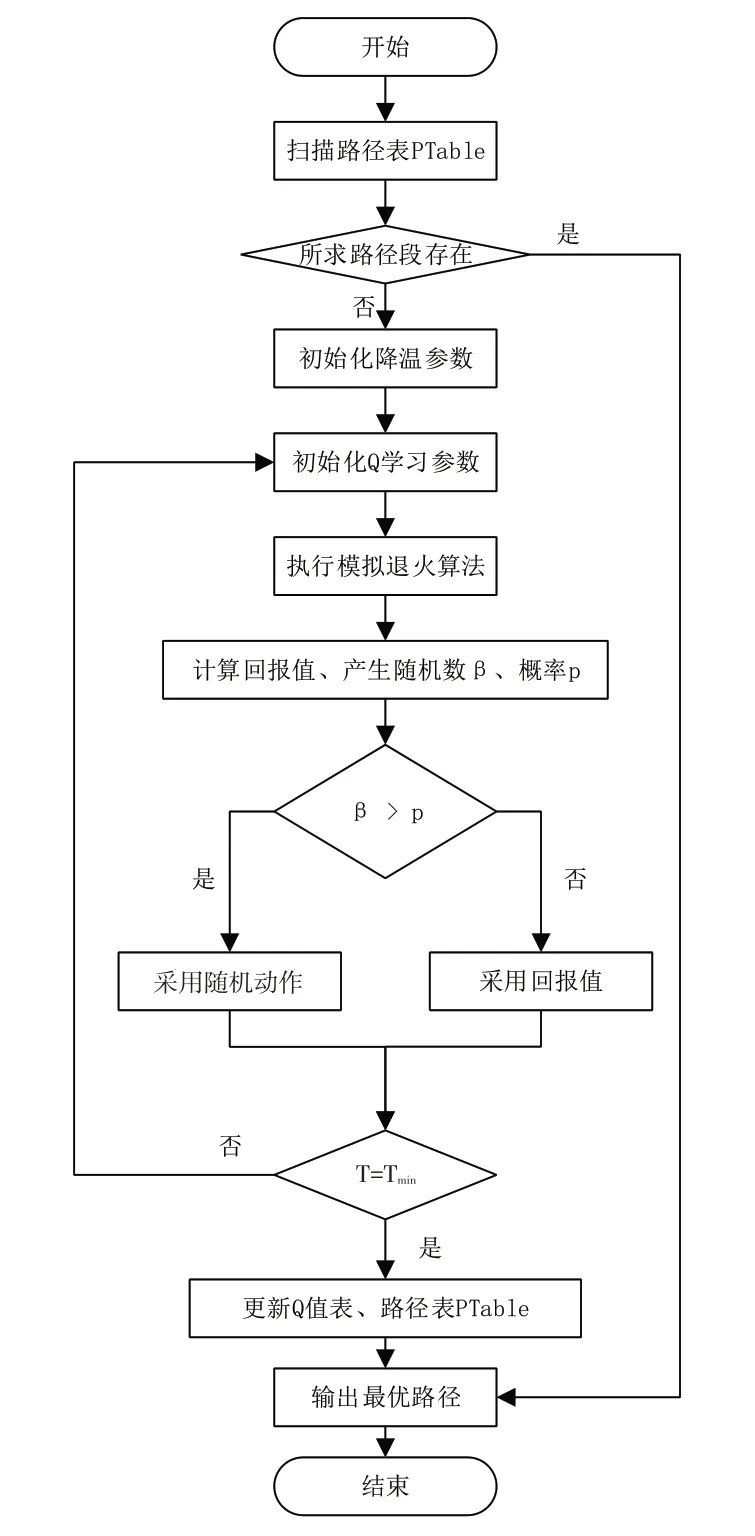
图2 改进Q 学习算法基本流程

5 仿真实验

5.1 实验描述

设计一个简单的方格“货到人”拣选系统环境（如图3所示），拣选环境模拟为26*26的栅格（单位：1），图中“START”和“GOAL”所在的区域分别为车辆的停车点和拣选台区域。中间部分8 个2*9 长方形黑色区域代表货架，其余17 个突起的灰色填充块状区域模拟静态仓储环境多AGV相遇情况。其中货架区域底部可走车。

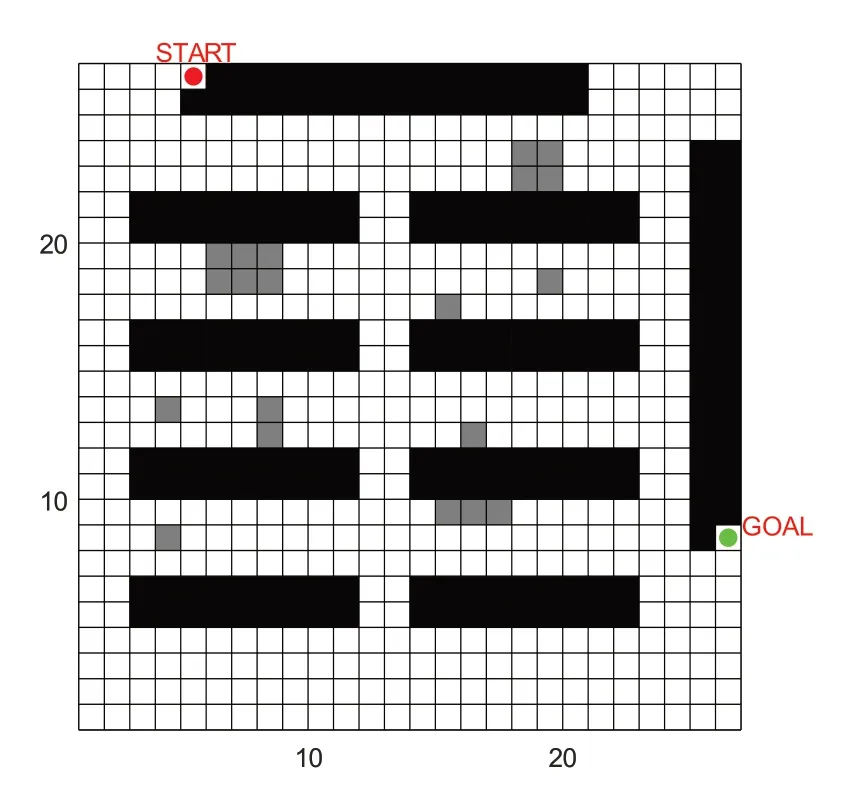
图3 仿真仓储环境图

给出5组任务，每组任务10个货物坐标点，随机给出每组任务的货架坐标和拣选台坐标点，任务逻辑为AGV从停车点出发，首先到达第一个任务货架，将货架运到拣选台，拣选完毕后将货架送回原位置，再走到下一任务货架，直至10个任务点全部走完，从拣选台返回停车点。

基于上述规则，比较在相同情况下分别采用改进Q学习和传统A*算法、传统Q学习算法时AGV的行驶距离长短，并且比较两种算法的寻路时间，来判断改进Q学习算法的有效性和优越性。其中，本次实验不考虑订单的任务分配问题，因此订单编号和位置均为随机，并未做归并处理。

5.2 实验结果与分析

模拟退火算法中规定初始温度T=1 000,终止温度Tmin=0.001，降温系数q=0.90。规定最大迭代次数为100 000 次。当迭代超过最大迭代次数时或寻到路径，本次寻路结束。在Q学习算法中，规定学习率α=0.7，折扣因子γ=0.95，奖励矩阵R如下：

给定5组路径信息（见表1），其中前三组为随机坐标点，第四组为第二组的对照组，拣选台同第二组重合，停车点为第二组停车点的相邻点，任务点坐标为部分重复点；第五组为第一组对照组，拣选台坐标为第一组相邻点，停车点坐标不同，任务点坐标与第一组部分相同或为相邻点。第四组、第五组用于测试路径表与改进Q学习的配合情况。

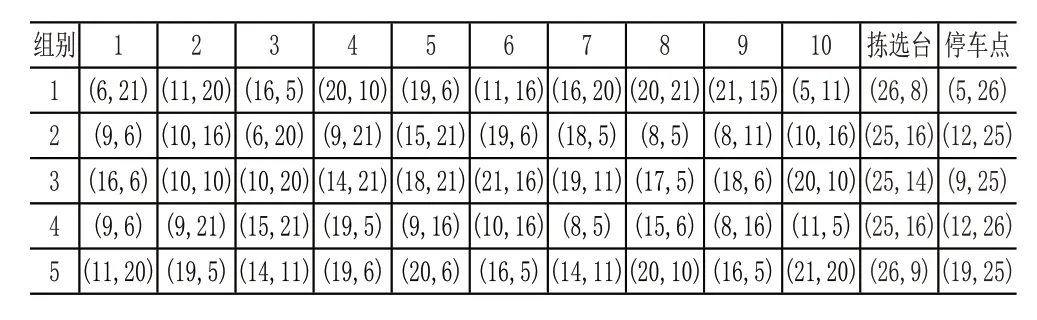
表1 任务点坐标

通过对比图4、图5可知，仓储环境中三种算法均能找到最短路径，寻路长度误差5%以内。寻路能力基本相同。但较于A*算法和传统Q学习算法，改进Q学习算法收敛到最优值的速度普遍快于其他两种算法的均值，效率最高可提高20%。由于改进Q学习算法引进了路径表，使第四组和第五组任务点寻路的效率大大提高，且具有一定的稳定性。

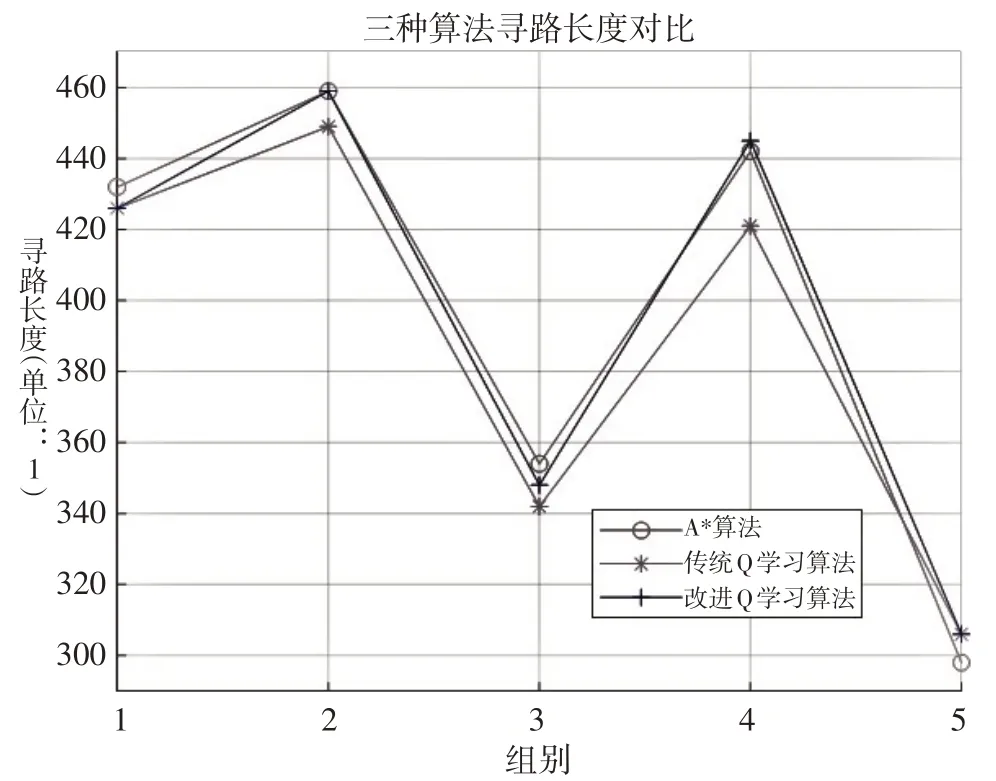
图4 三种算法寻路长度对比

图5 三种算法收敛对比

6 结语

本文针对“货到人”拣选系统，提出一种结合动态探索因子和路径表的改进Q学习算法，来改善传统Q学习算法效率低下、容易陷入局部最优解的问题。首先引入动态探索因子，将传统Q学习的最优选择策略以一定的概率实现，并提出路径表的概念，一定程度上节省了探路成本。然后建立栅格环境模拟仓储，通过仿真实验，将改进Q学习算法和传统Q学习、A*两种算法对比，得出在“货到人”拣选背景下仓储物流机器人AGV 的拣货路径最短。通过实验，改进Q学习算法能够找到最优解，并且收敛速度优于传统A*算法和传统Q学习算法，在一定程度上体现了该算法的高效和可用性。