基于遗传算法的飞机机翼结构拓扑优化设计方法
2021-01-10周志强胡宗浩邢本东崔灿
周志强 胡宗浩 邢本东 崔灿


摘要:为了降低飞机机翼结构的位移变化幅度,合理优化飞机机翼结构,开展基于遗传算法的飞机机翼结构拓扑优化设计方法研究,通过飞机机翼编码矩阵、检查拓扑结构外形、设计飞机机翼拓扑结构标准化约束条件、转换飞机机翼结构适应值,完成优化设计。通过对比实验证明,设计方法在应用到实际飞机机翼结构优化中时,能够实现对其结构的合理设计,提高机翼的承载能力,进一步实现对结构总重的降低,为飞机飞行安全提供保障。
Abstract: In order to reduce the displacement variation range of aircraft wing structure and reasonably optimize aircraft wing structure, the topology optimization design method of aircraft wing structure based on genetic algorithm is studied. The optimization design is completed by aircraft wing coding matrix, checking the topology shape, designing the standardized constraints of aircraft wing topology structure, and converting the fitness value of aircraft wing structure. Through comparative experiments, it is proved that when the design method is applied to the structural optimization of actual aircraft wing, it can realize the reasonable design of its structure, improve the bearing capacity of the wing, further reduce the total weight of the structure, and provide guarantee for aircraft flight safety.
关键词:遗传算法;飞机;机翼结构;拓扑;优化设计;方法
Key words: genetic algorithm;aircraft;wing structure;topology;optimization design;method
中图分类号:TU311.41 文献标识码:A 文章编号:1674-957X(2021)24-0016-03
0 引言
在现代化高速发展的时代背景下,与机械制造相关、与机械生产发展水平相关的行业综合水平,成为了评估国家科研制造能力的关键指标。为了提高飞机科研制造水平,我国在此方面投入了大量的人力与财力,致力于开发功能更加全面、结构更加完善的飞机。机翼是构成飞机主要结构,在飞机飞行过程中,机翼主要负责提供飞机上升的动力,因此,机翼整體结构的合理性,将直接干预到飞机在飞行中的多种性能。在掌握机翼在整体结构中的重要性后,技术单位便开始了对传统飞机机构进行优化设计[1]。在传统的机翼结构设计过程中,设计师大多是基于主观判断,实施结构设计工作。并在完成结构的基础设计后,对机翼的综合性能进行检验,倘若在检验中发现结构存在不合理问题,便需要设计师反复进行结构的修改与优化。尽管此种方式可以使最终集成在飞机上的机翼结构满足飞行需求,但在此过程中却需要设计人员持续投入精力,不仅工作烦琐,同时也会由于设计过程中缺少一个统一的结构标准,导致设计过程周期长、效率低。为了解决此方面的问题,在本文的研究中,引进遗传算法,采用在终端计算机上进行结构布局分析的方式,实现对机翼结构的拓扑优化,从而实现对我国机械制造综合水平的提升。
1 基于遗传算法的飞机机翼结构拓扑优化设计方法
1.1 基于遗传算法的飞机机翼编码矩阵
为了实现对飞机机翼结构的拓扑优化,在本章的研究中,引进遗传算法,结合机翼结构构成材料的细部结构性能与宏观结构性能函数关系,掌握设计飞机机翼结构时的最优函数表达式[2]。在此过程中,通过遗传算法进行结构的分析,可以获得性能更优的宏观力学参数,从而为后续相关优化设计工作提供参考。
为了满足本文设计要求,在开展此方面内容的研究时,可采用建立飞机机翼结构构成复合材料微观结构与宏观结构性能函数关系的方式,进行整体结构拓扑关系的描述。并通过对细部结构的优化设计,掌握整体结构的宏观力学能力。在设计编码函数时,为了实现机翼整体结构与HFGMC函数呈现匹配或对接状态,可将遗传算法进行二维二进制编码表达方式,即产生的染色体均由“1”与“0”构成,数字排列组合形成一个数字阵列。考虑到二维二进制编码方式存在一定特殊性,二进制数值交叉点可能存在缺陷,因此,可在此步骤进行结构断点交叉的改进。选择轮换法,进行结构交叉点的正点选择,根据结构整体数值的正比概率,进行染色体的选择,选择后可以生成一个新的编码种群[3]。为了降低染色体变异对编码形式的影响,可通过调整染色体基因的方式,对编码过程进行加速处理,即使前端的结构交叉点(父代交叉点与子代交叉点)同时参与下一种群的竞争。
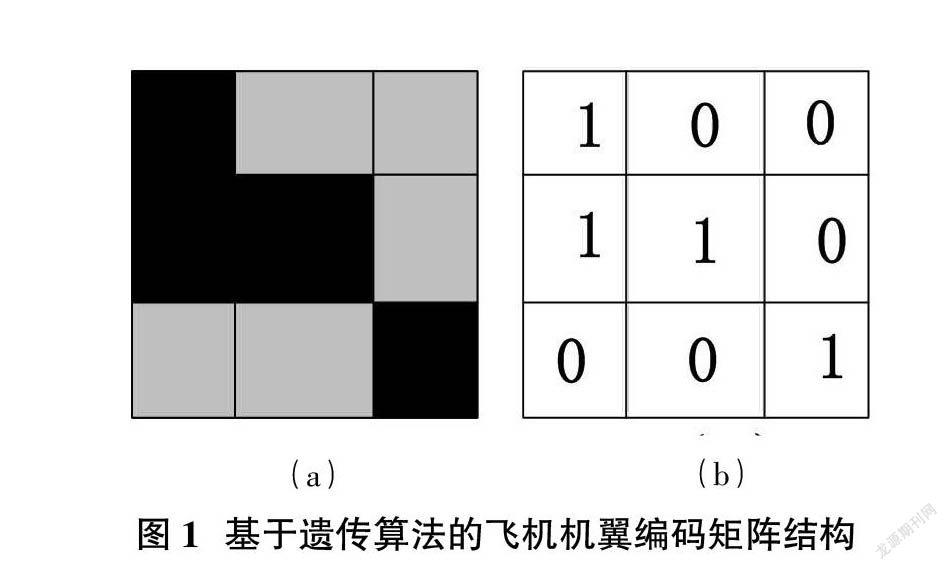
在掌握基于遗传算法的编码原理后,将对应的子代编码与HFGMC函数进行匹配。假设在此过程中飞机机翼结构的细部结构具有对称性特点,因此,可选择结构中的1/4结构作为一个染色体,其中HFGMC函数使用“0”与“1”进行描述,构成一个数字矩阵。矩阵结构如图1所示。
图1(a)中,黑色图片区域表示细部结构中的纤维结构;灰色图片区域表示为细部结构中的基体结构。对应图1(b)中,网格“1”对接纤维结构;网格“0”对接基体结构。按照此种方式,对飞机机翼编码矩阵进行拓展,以此实现对飞机机翼结构编码矩阵的构建。
1.2 拓扑结构外形检查
在完成对飞机机翼编码矩阵的构建后,需要根据编码结构与编码的顺序,进行拓扑结构外形适配性与合理性的检查。考虑到机翼整体结构的拓扑参数与外形均为遗传操作随机处理生成的,因此,在生成整体结构时,难免会出现由于遗传处理操作不当导致的不稳定问题,尤其是在机翼桁架结构中,当拓扑结构出现异常时,甚至会出现机翼损坏等方面的问题。为了实现对此种问题的规避,应采取有效的措施进行整体结构稳定性的核查。通常情况下,相关此方面的设计研究可从总刚度的矩阵正性结构性能来判断。当识别后矩阵为正定性,可以认为构建的飞机机翼拓扑结构矩阵具有稳定性特点,反之,可认为构建的飞机机翼拓扑结构不稳定。对于此过程中的不稳定结构,无需对其进行下一步骤的结构处理与分析,可直接将此部分结构作为不可行解的个体,并通过对其采取适度惩罚的方式降低结构与整体的适配度即可。
在随机生成的飞机机翼拓扑结构中,可能发生的另一种情况包括:当整体结构中的部分结构没有与杆件发生连接行为时,可以认为此时的节点在整体结构中处于独立状态,即此部分节点为无用节点,需要根据整体结构的优化设计需求,对其进行删除处理。同时,考虑到飞机机翼拓扑结构中的不同节点连接情况是不同的,此种行为会导致结构整体的总刚度与矩阵维度出现不适配的问题。为了降低或避免由于此方面问题造成的拓扑结构不稳定现象发生,简化对拓扑结构计算的步骤,可以采用基础结构总刚度生成的方式,进行节点的删除。但直接删除拓扑结构中的节点会造成基础结构刚度矩阵出现奇异现象,因此,对于删除的拓扑结构,需要对其进行矩阵修正与补偿处理。修正与补偿的过程为:以被删除的节点位置作为补偿支座,引进结构有限元处理模型,按照“主节点补偿1,辅助节点补偿0”的方式,进行整体结构架构的优化补偿。按照此种处理方法进行结构的优化处理,不仅可以实现将被删除节点的位移约束值保持“0位移”,也可以确保飞机机翼拓扑结构中的刚度矩阵对非奇异性问题的规避。
除上述提出的内容,可直接采用外观异常检查的方式,进行结构基础变量的分析,并根据基础结构的异常点,进行刚度矩阵的细致化修复。对于在此过程中较为精密的结构构件,可采用建立统一标准数学模型的方式,进行个体或细部结构与整体结构适配性的分析,通过此种方式,实现对飞机机翼拓扑结构的精密调整,从而确保对整体拓扑结构外形检查工作的有效性,为后续结构优化设计提供基础数据作为支撑。但在此过程中应注意的是,此方面工作的实施还需要根据机翼整体结构与其规模实施,并根据前端的优化设计需求,进行检查方案的调整。
1.3 飞机机翼拓扑结构约束条件标准化设计
在完成上述相关研究后,可根据机翼结构设计过程中,使用复合材料的细部力学性能,进行飞机机翼结构与基体结构之间函数关系式的表达[4]。表达式如下:
公式(1)中:W表示为飞机机翼结构受力;?琢表示为桁架结构;A表示为截面面积,计算单位为m2;i表示为结构位置;n表示为设计量;j表示为拓扑变量;G表示为循环动力;L表示为飞机机体长度。根据上述计算公式,可以得出飞机机翼结构在飞机飞行过程中的受力受到多种因素的影响,而要实现对机翼结构的拓扑优化,应当从多个因素层面考虑,设定对应的约束条件,以此种方式,确保优化后的结构具有更高的性能。
在此过程中,将飞机机翼结构复合材料细部结构的数据矩阵作为设计变量,将不同材料的力学性能作为目标函数,进行机翼结构纤维体积的百分比约束,约束的标准可参照下述计算公式:
公式(2)中:f表示为飞机机翼结构的宏观力学性能;X表示为机翼结构构成材料的设计参数,对应数据矩阵中的“0”与“1”;S表示为纤维结构;T表示为基体结构;Vf表示为纤维结构占机翼结构的百分比;Vi表示为选择结构中有效力学结构占机翼结构的百分比。按照上述计算公式,可实现对飞机机翼拓扑结构的约束。为了确保约束的条件与飞机机翼结构拓扑优化设计具有一致性特点,需要数字转换与交易的过程进行改进,改进的过程可采用对交叉点进行断点处理的方式进行,并通过对断点的处理,进行微观结构或细部结构约束条件的建模,以此为依据,进行不同行或不同列断点位置约束条件的建模,输出所有可用于约束断点交叉的条件,以此种方式,完成对此方面内容的设计研究。
1.4 融合约束条件的结构适应值转换
在掌握飞机机翼拓扑结构优化设计的约束条件后,可将对应的约束条件作为参照,进行机翼拓扑结构适应值的转换,将转换后具有较强适应性的结构值作为约束值,以此种方式,实现对飞机机翼拓扑结构的优化设计。在此过程中,考虑到改进结构交叉点具有一定的随机性,但仅按照二进制数值进行结构交叉改进的次数却是有限的[5]。具体包括“1-0”、“1-1”、“0-0”、“0-1”,为了简化转换的次数,可按照二进制数值转换方式,进行交叉点的选择与改进。此时,可先产生一个随机数值r,通过判断数值的奇偶性,决定结构交叉点调整数值时按照行结构排列或是按照竖向结构排列。在此基础上,产生另一个随机数a,按照随机数r的判断方式,决定染色体是否发生前端替换。按照此种方式,对飞机机翼编码矩阵进行重组。
完成矩阵数据的重构后,为了确保初始化的种群可以遍布整个分布空间,可实现对机翼结构形态的描述,获取结构中的等分结构点,作为初始化群体点。在此基础上,为了满足计算机的二进制数值存储方式,可将对应的二进制数值以物理方式存储在设备终端,直接使用调用程序,进行“1”与“0”的排序,确保优化后的交叉点与二进制点呈现对接关系后,便可以认为实现或完成了对适应值的转换。按照转换后的适应值进行機翼结构的优化设计,实现对结构拓扑的综合优化。
2 对比实验
结合本文上述论述内容,从理论层次实现了对基于遗传算法的飞机机翼结构拓扑优化设计方法的理论设计,为进一步验证该方法的实际应用效果,选择以某飞机机翼生产加工企业为依托,针对其某一架飞机机翼规格对其结构进行拓扑优化设计。已知该飞机机翼肋板结构的规格为450mm×250mm,通过本文上述飞机机翼编码矩阵得出该机翼肋板的单元数量为45×25,其弹性模量为2.8×109,泊松比常数为0.28。在实验过程中,为了方便分析,假设该机翼结构只会受到载荷的影响。结合上述参数,分别利用本文提出的设计方法和基于气动弹性载荷的设计方法对该飞机机翼结构进行优化设计。完成设计后,为验证两种飞机机翼结构的性能,选择将受到多种不同应力时的结构位移情况作为评价指标,若在受到应力作用时,飞机机翼结构的位移变化幅度较小,则说明该结构承载能力越強,结构设计越合理,反之,位移变化幅度越大,则说明该结构承载能力越弱,结构设计越不合理。在对飞机机翼结构位移测量时,采用结构光三维测量仪对飞机机翼结构水平方向和竖直方向上的位移进行测量,并将得出的结果绘制成表1所示。
表1中,X表示为水平方向上的结构位移;Y表示为竖直方向上的结构位移。从表1中得出的实验数据可以看出,因此,通过上述实验证明,本文提出的设计方法在应用到实际飞机机翼结构优化当中时,能够实现对其结构的合理设计,并提高机翼的承载能力,为飞机飞行安全提供保障。同时,为了进一步探究本文提出的设计方法在实际应用中是否能够起到降低飞机机翼结构总重的作用,分别选择四种不同的飞机机翼规格,在两种设计方法的基础上,设计并生产出四个飞机机翼,针对其结构总重进行测量。选用PD-CT230PLUS型号测量装置,对两种设计方法分别生产出的四个飞机机翼总重进行测量,该型号测量装置测量精度为0.01kg,能够充分满足本文实验精度需要。将PD-CT230PLUS型号测量装置测量得到的数据进行记录,并将其绘制成如图2所示的飞机机翼结构总重图。
从图2中绘制的两条曲线可以看出,基于气动弹性载荷的设计方法中飞机机翼的结构总重均超过700.00kg,并且编号为1、3、4三种飞机机翼其结构总重甚至超过800.00kg,严重不符合飞机机翼结构的设计和生产需要,无法将其应用到飞机结构安装当中。而本文设计方法中飞机机翼的结构总重均未达到600.00kg,并且编号为2的飞机机翼结构总重仅为500.52kg。因此通过上述得出的实验结果进一步说明,本文设计方法下四种飞机机翼的结构总重均明显小于基于气动弹性载荷的设计方法。通过上述实验得出的两种数据结果综合分析得出,本文设计方法在实际应用中可以在保证飞机机翼结构质量的情况下,使得设计精度更高,并且实现对其结构总重的降低。将本文提出的设计方法应用到实际可以实现对飞机机翼结构的全面优化,进而提升飞机制造行业的综合水平。
3 结束语
本文引进遗传算法,从飞机机翼编码矩阵、拓扑结构外形检查、拓扑结构约束条件标准化设计、结构适应值转换四个方面,提出一种针对飞机机翼结构的拓扑优化设计方法。为了证明设计后的方法在实际应用中具有较高的实用性,进一步设计了对比实验,经过实验证明,设计的方法在实际应用中,具有较显著的优化效果,可实现对飞机机翼结构性能的有效改善,在实际应用中可以在保证飞机机翼结构质量的情况下,使得设计精度更高,并且实现对其结构总重的降低。但此次实践研究受到时间与实验设备的限制,仅从单个方面进行了方法的检验,未能从多个方面进行方法有效性的验证。因此,此次研究成果仅能作为参照,仍需要在后续的研究中,对此方法进行多个维度的有效性检验。并在实践应用中定位此方法在功能方面存在的不足,以此种方式,为对我国现代化飞机制造行业的发展提供完善的策略,为电子制造与精密零构件的开发与设计提供技术层面的有效指导。
参考文献:
[1]刘晓晨.考虑结构失稳特征的复合材料机翼气动弹性优化设计[J].力学与实践,2020,42(05):571-575.
[2]郭文杰,常亮,王立凯,等.基于HAJIF系统的复合材料机翼结构优化[J].高科技纤维与应用,2021,46(03):65-70.
[3]李东辉,杨凤田,马宏图,等.基于气动弹性载荷的电动飞机复合材料机翼结构优化及试验验证[J].科学技术与工程,2020,20(18):7516-7523.
[4]邱福生,赵红娟,戴良景,等.考虑气动-结构耦合的机翼三维结构拓扑优化方法[J].科学技术与工程,2019,19(22):350-355.
[5]曾杰,钱文敏,肖志鹏,等.复合材料机翼结构的气动弹性优化设计与风洞颤振试验[J].航空科学技术,2019,30(09):120-129.
