基于模糊控制算法的移动机器人路径纠偏研究
2021-01-10卢惠林
卢惠林
(无锡商业职业技术学院 物联网技术学院, 江苏 无锡 214153)
跨仓库巡检移动机器人路径跟踪系统负责完成路径纠偏、速度控制、安全避障等任务,也即在各种路况中完成预设的导航任务。为了更好实现移动机器人路径跟踪,本文重点研究模糊控制路径纠偏算法。
模糊控制算法以模糊语言变量、模糊集合论和逻辑推理为基础,将输入输出状态进行模糊化处理,根据规则库计算控制输出,再将输出解模糊化输出至被控对象。邹细勇等人提出了一种基于分阶段的移动机器人模糊控制路径跟踪方法,将路径跟踪分为趋近和稳定两个阶段,各阶段拥有对应的模糊化比例因子,可实现快速纠偏后平稳行驶[1]。
一、路径跟踪系统的组成
移动机器人路径跟踪系统组成如图1所示,移动机器人在预设路径上行驶到各工位点,通过感知层—决策层—执行层,完成路径跟踪。预设路径包括色带路径、双磁钉路径以及RFID地标,在仓库区动态运行过程中,移动机器人还需要处理障碍物“占道”的特殊情况。
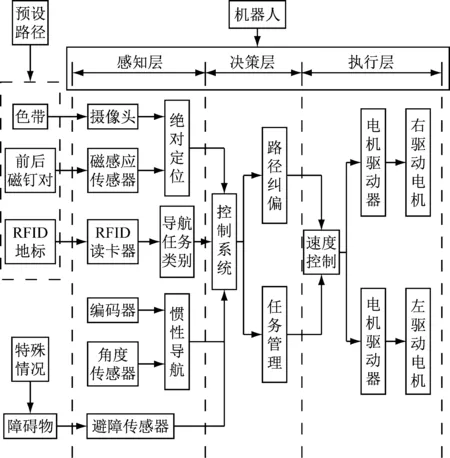
图1 路径跟踪系统组成框图
移动机器人感知层包括摄像头、磁感应传感器、RFID读卡器、编码器、角度传感器以及避障传感器。摄像头与磁感应传感器构成了移动机器人的绝对定位系统,编码器与角度传感器构成了惯性导航系统。由于外部环境的影响以及内部传感器的累积误差,移动机器人的行驶轨迹相对于预设路径会发生偏差,这时需要通过绝对定位信息来对移动机器人位姿进行纠偏。RFID地标可通过写卡器对其进行任务号编排分配,配备读卡器的移动机器人运行到对应RFID时,则会根据其预设的导航任务,实现工位点的启动、停止、左右转、加减速以及绝对定位模式切换。感知层信息通过数据传输的方式,将传感器信息传送到决策层,决策层主要包括路径纠偏以及导航任务管理。本研究采用模糊控制算法实现移动机器人路径纠偏,采用STM32内部中断优先级机制实现其导航任务管理,决策层会根据移动机器人自身姿态、绝对定位信息以及RFID任务,决策出移动机器人下一时刻左右轮的速度。执行层则根据决策层输出的速度信息,通过PID算法控制左右轮电机转速,最终完成路径跟踪。本文对模糊控制路径纠偏算法、速度控制PID算法以及导航任务管理方法进行研究。
二、路径纠偏的模糊控制算法
(一)算法流程
路径纠偏是跨仓库巡检移动机器人路径跟踪导航中最重要的一环,其算法设计质量直接影响路径跟踪导航精度。目前常用的路径跟踪算法有滑膜控制、反馈线性化、神经网络等,移动机器人在仓库区非结构路面运动过程中,其系统具有时变性、非线性等特性,难以建立明确的数学模型,所以需要一个非线性智能控制算法来实现路径跟踪。模糊控制算法以模糊语言变量、模糊集合论和逻辑推理为基础,具备高实时性、高适应性、高鲁棒性等优点,非常适合在该环境下使用[2]。
基于模糊控制的路径纠偏算法流程如图2所示。当感知层绝对定位系统(磁感应传感器/摄像机)检测到移动机器人相对于预设路径发生角度偏差和距离偏差(Δα、Δu)后,通过通信系统将偏差数据发送给决策层的模糊控制路径纠偏算法。算法在每个控制周期将偏差数据(Δαt、Δut)作为输入变量,经过模糊控制决策,输出左右轮速差ΔV给执行层,执行层使用PID速度控制算法,将左右轮速快速且稳定地调节到期望速度值。如此循环,直到将绝对定位检测到的惯性导航累计误差消除,移动机器人快速地调回预设路径后平稳行驶[3-4]。
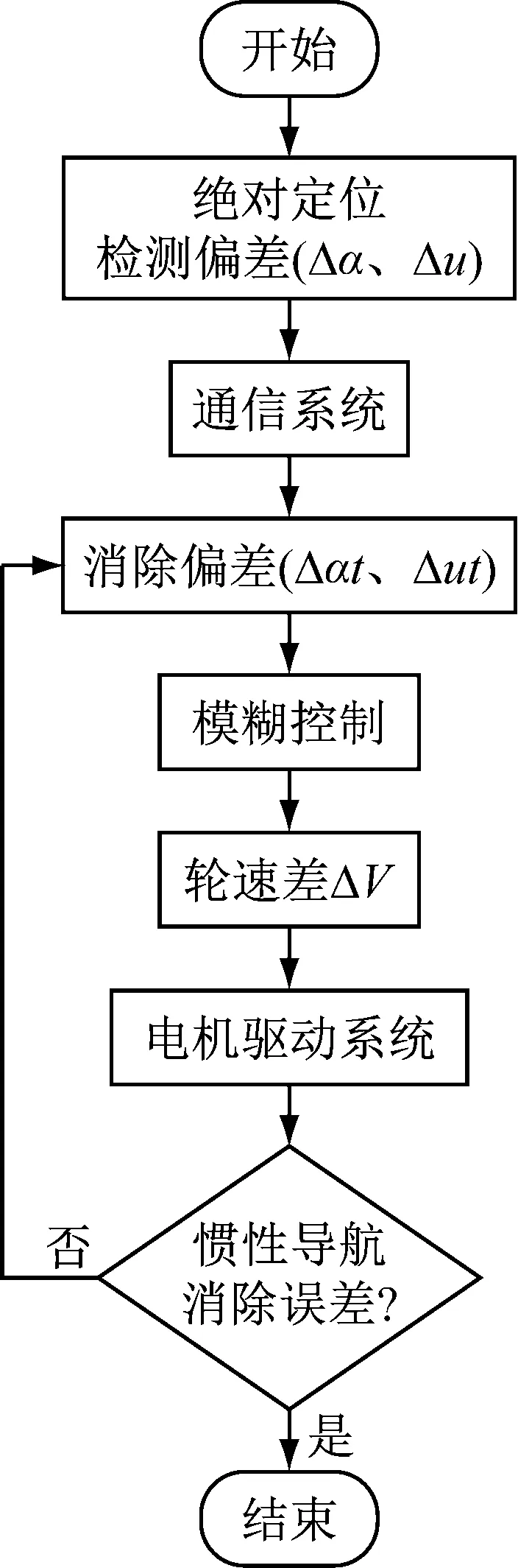
图2 路径纠偏流程图
模糊控制算法如图3所示,首先将输入变量模糊化处理,在每个伺服周期,控制算法会根据输入变量所处的模糊论域,去查离线制定好的模糊规则控制表,得到输出变量的模糊值,经解模糊后,得出下一个伺服周期的轮速差ΔV。
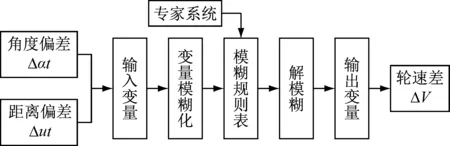
图3 模糊控制算法
(二)变量模糊化
变量模糊化是将输入变量、输出变量基本论域转换为模糊控制算法能够识别的模糊论域。本文以角度偏差、中心偏差数据(Δαt、Δut)作为输入变量,左右轮速差ΔV作为输出量,设计了一个双输入单输出的二维结构形式的模糊控制器。
根据传感器检测范围与实地环境,设定移动机器人偏离路径时,角度偏差极值为±10°,中心偏差极值为±100 mm。当通过绝对定位系统检测偏离路径值超过设定极值后,则认为巡检移动机器人脱轨。因此角度偏差的基本论域为[-10°,10°],中心偏差的基本论域为[-100 mm,100 mm]。由此得出:角度偏差的模糊子集为{NB,NM,NS,ZE,PS,PM,PB},模糊子集分别代表极左偏、左偏、微左偏、正中、微右偏、右偏、极右偏,角度偏差模糊论域为{-3,-2,-1,0,1,2,3};中心偏差的模糊子集为{NB,NM,NS,ZE,PS,PM,PB},模糊子集分别代表极左偏、左偏、微左偏、正中、微右偏、右偏、极右偏,中心偏差模糊论域为{-3,-2,-1,0,1,2,3}。
本文所选直流电机最快转速是10 rad/s,为保障移动机器人行驶平稳性和纠偏快速性,设定左右轮轮速调整范围上下浮动不超过1 rad/s,则左右轮速差的基本论域为[-2,2]rad/s,左右轮速差模糊子集为{LVB,LB,LM,LS,ZE,RS,RM,RB,RVB},模糊子集分别代表左极速、左快速、左中速、左慢速、无速差、右慢速、右中速、右快速、右极速;左右轮速差模糊论域为{-4,-3,-2,-1,0,1,2,3,4}。
基本论域值属于模糊论域的程度高低称之为隶属度,论域之间通过隶属度函数相互关联。常用隶属度函数有三角形、高斯形和梯形隶属度函数。
三角形隶属度函数对误差反应较为敏感,适合快速路径纠偏,但是误差在零点附近时移动机器人会左右抖动。三角形隶属度函数定义如下:
(1)
高斯隶属度函数可以在保证纠偏快速性的同时,解决车身抖动问题。高斯隶属度函数定义如下:
(2)
梯形隶属度函数的功能与三角形函数恰恰相反,对误差反应不敏感,适合误差值距离零点较远时使用,避免频繁调控。梯形隶属度函数定义如下:
(3)
根据各隶属度函数的特点,设立输入变量、输出变量隶属度函数,如图4所示。
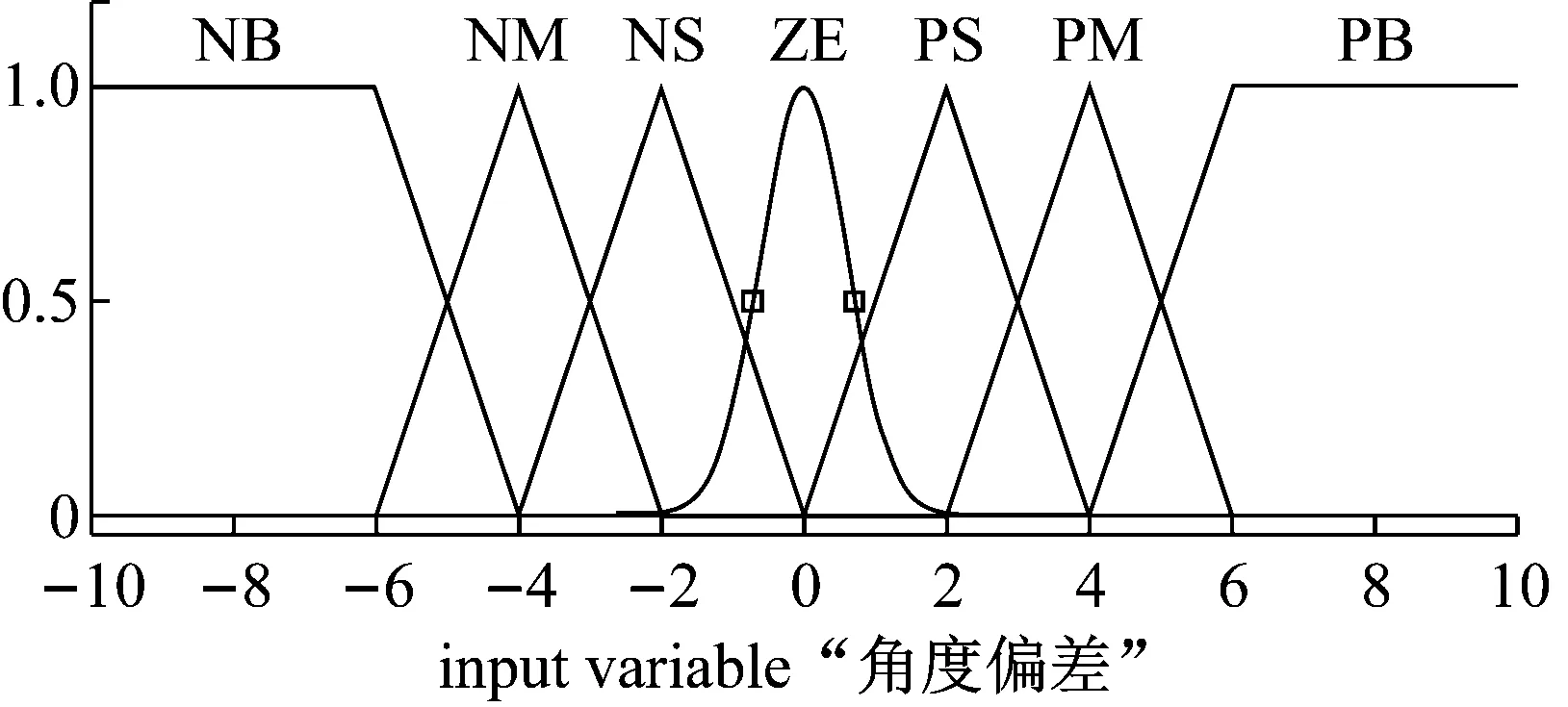
a. 角度偏差Δαt隶属度函数
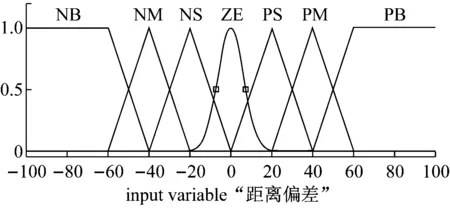
b. 距离偏差Δut隶属度函数
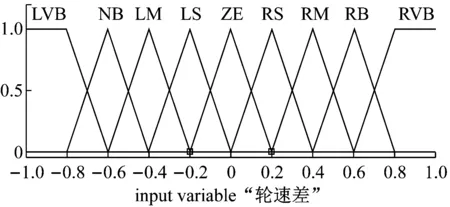
c. 输出变量左右轮速差ΔV
(三)模糊规则建立
移动机器人模糊控制规则通过人工控制经验总结而来,可根据专家经验法,设置模糊控制规则。借鉴驾驶汽车的经验,当由外部绝对定位检测到移动机器人相对于预设路径发生偏差时,移动机器人根据当前车体位姿与预设路径偏差情况,调节左右轮速度,重新回到预设路径。当车体位姿与预设路径无偏差时,保证左右轮速度无差值即可;当车体位姿与预设路径有较小偏差时,微调左右轮速,回到预设路径;当车体位姿与预设路径有较大偏差时,在保证安全行驶的前提下,迅速调节左右轮速度,使车体快速回到预设路径上[5]。
结合对移动机器人运动学模型与误差模型的分析,可得49条模糊控制规则:
R1: if Δαis NB and Δuis NB then ΔVis LVB
R2: if Δαis NB and Δuis NM then ΔVis LB
…
R49:if Δαis PB and Δuis PB then ΔVis RVB
将上述模糊控制规则语句转换成移动机器人模糊控制规则表,如表1所示。
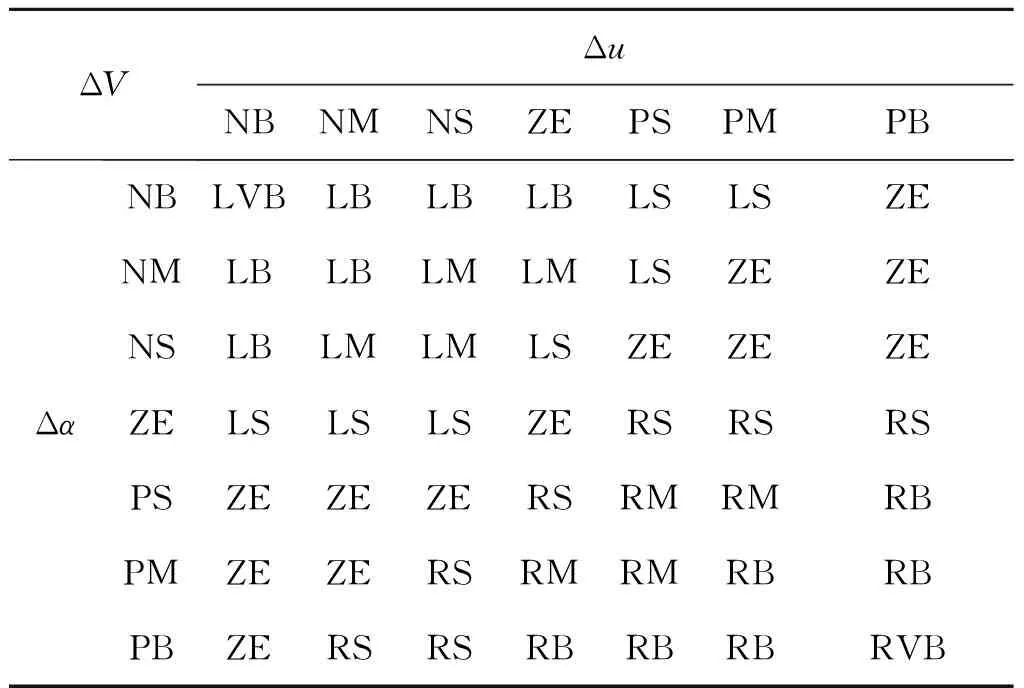
表1 模糊规则控制表
在MATLAB中将规则表输入fuzzy模块中,如图5所示。
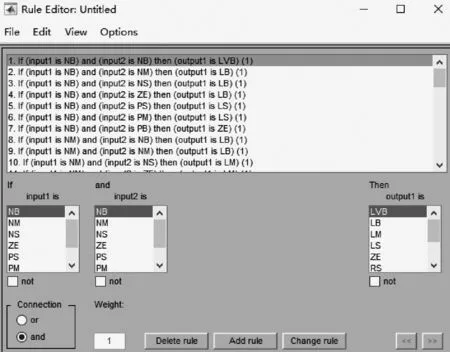
图5 模糊控制规则
(四)输出解模糊
建立模糊规则控制表之后,算法输出量依然是模糊量,要将输出模糊量实际反应在轮速差上,还需要进行解模糊,所谓解模糊就是将模糊集合映射为一个清晰值。模糊控制中常用的3种解模糊方法为:最大隶属度法、中位数法、重心法。
① 最大隶属度法:
μC′(Z0)≥μC′(Z),Z0∈Z
(4)
该方法只输出隶属度最大的对应的清晰值Z0,忽略了其余隶属度函数对输出结果的影响,适合控制要求不高的场合。
② 中位数法:
(5)
该方法以隶属度函数与坐标轴围成的面积求清晰值,面积均分点即为清晰值。该方法计算较为准确,但没有考虑到各隶属度函数所占的权重。
③ 重心法:
(6)
式(6)中,uc表示隶属度,Zi表示隶属度输出语言值。
本文考虑到输出变量清晰值的准确性,选择重心法解模糊,将输出模糊集的隶属度、权系数与输出论域上的点进行加权平均,得到输出变量的清晰值。
三、模糊控制算法仿真分析
经中心法解模糊后,在MATLAB中可看到模糊控制路径纠偏算法输出曲面,如图6所示。在路径偏差较小时,控制策略偏灵敏,三角形隶属度函数可根据输入变量的偏差情况,实时计算出相应的轮速差来缩小误差;而路径偏差在零点附近时,曲面图偏平缓,通过高斯隶属度函数可避免移动机器人零点抖动问题;在路径偏差较大时,曲面图中各平面间相对较陡,梯形隶属度函数可在较少更改轮速差的前提下将误差快速缩小。
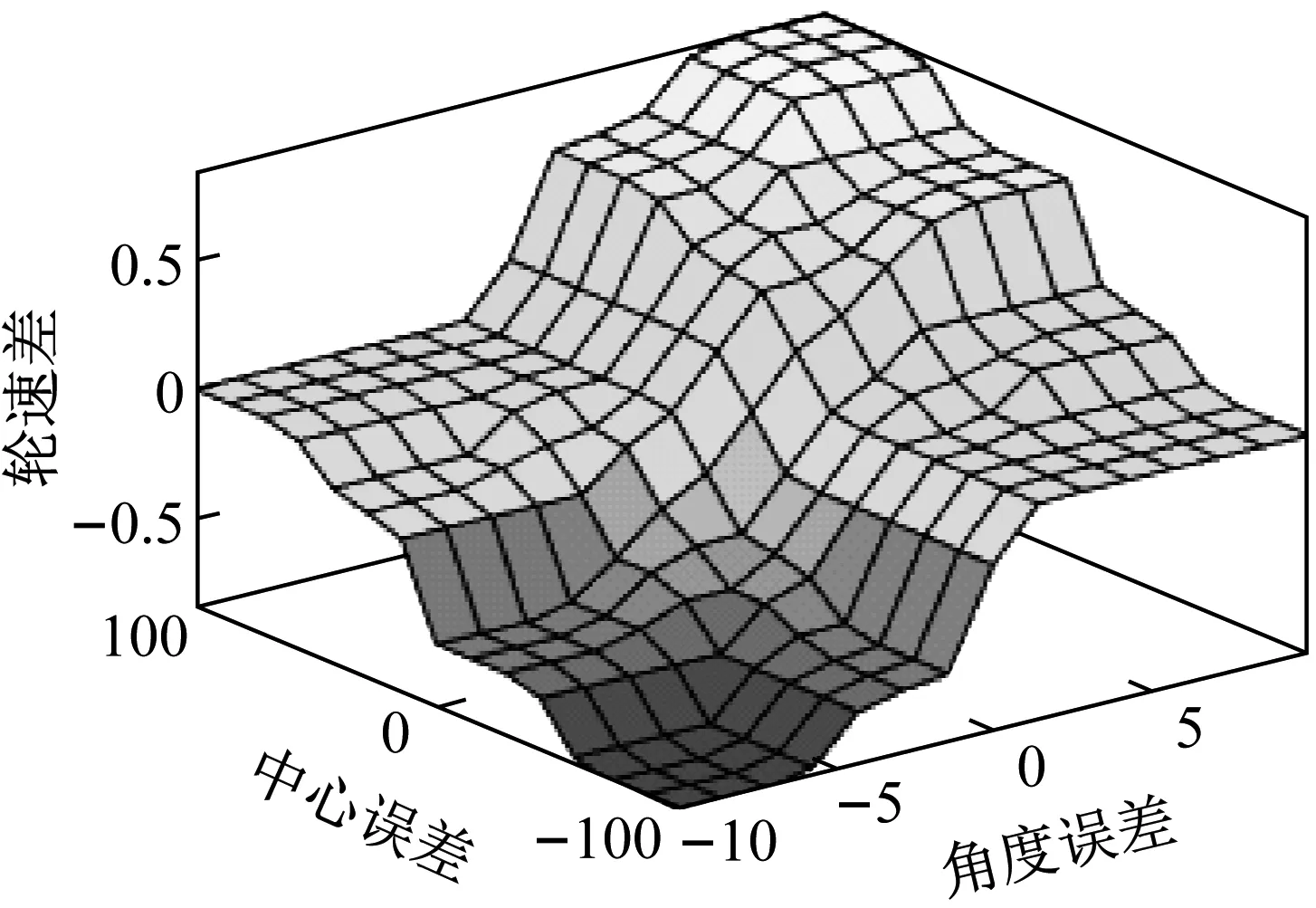
图6 控制输出曲面
图7为该模糊控制器的控制规则观测窗口。通过该观测窗口可以观测角度偏差和中心偏差输入变量变化时,对应的轮速差输出变量的清晰值,如当角度发生左偏差、中心无偏差时,轮速差为负,代表左轮加速、右轮减速(若为正,则左轮减速、右轮加速)。经多次验证,发现该模糊控制器控制效果与预期一致,如表2所示。
经模糊控制算法输出轮速差,系统需要在最短时间内控制驱动电机达到目标转速。本研究选择的电机为直流电机,其控制方法为利用控制器中的定时器产生PWM波来控制其转速, 如图8所示。在PWM调速系统中,在不改变脉冲周期的条件下,改变一个周期中高低电平出现时间,实现改变占空比,从而改变电机电枢两端平均电压,调整电机的转速。
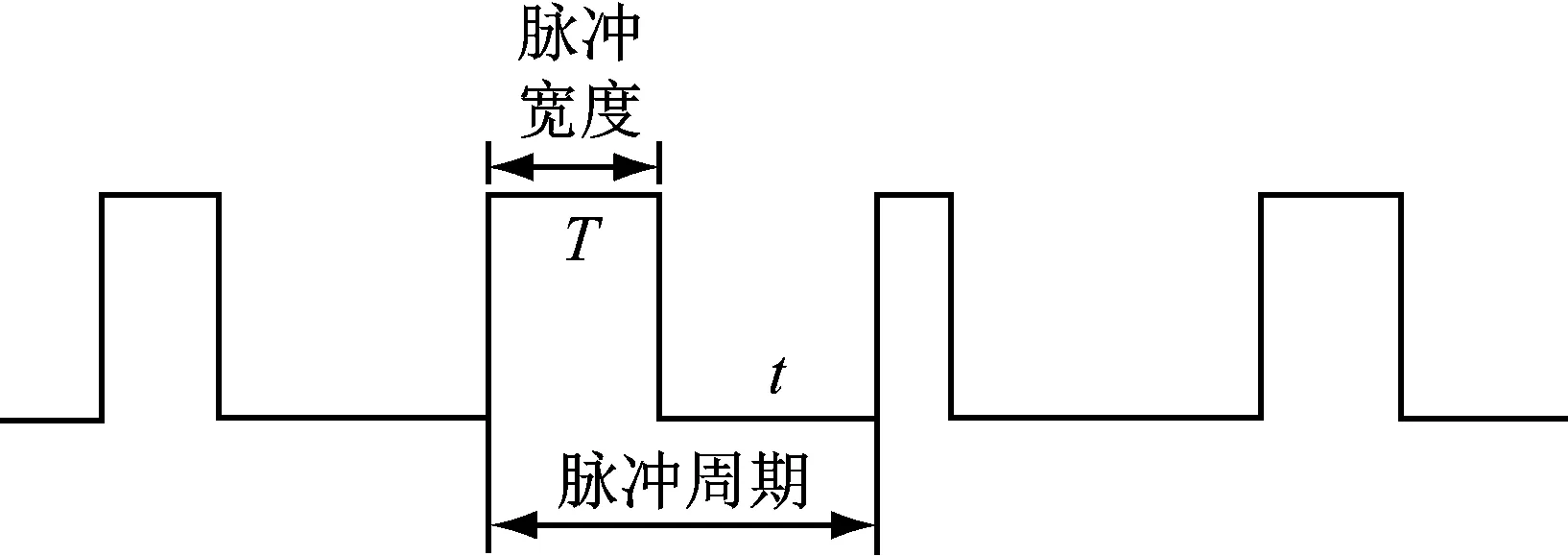
图8 PWM波示意图
假定Vmax为电机最高转速,D=T/t为占空比, 则电机的平均速度Vd=D×Vmax。由此可知,当改变占空比D时,就可以改变电机平均速度Vd,实现调节电机速度的目的。直接使用PWM波控制电机转速,这样的开环控制不能达到精准控制电机转速的目的,需要通过闭环控制电机精准、快速地达到目标速度,如图9所示。
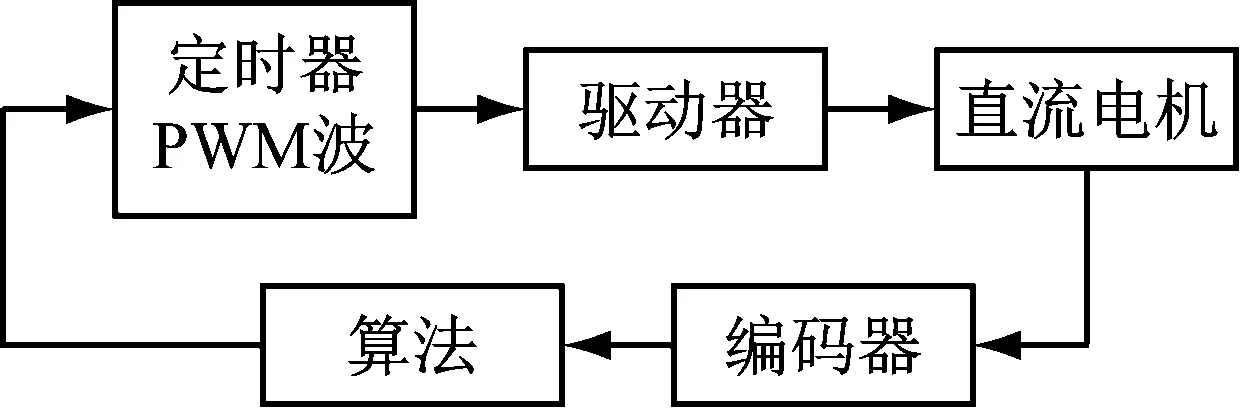
图9 闭环控制示意图
本文选择增量式PID算法闭环控制电机转速,当通过编码器计算检测到电机当前转速与期望转速有误差时,则会根据当前两次的误差值,通过增量式PID算法计算输出电机转速增量,进而控制PWM波占空比,使电机达到目标速度。PID算法控制电机转速流程如图10所示。
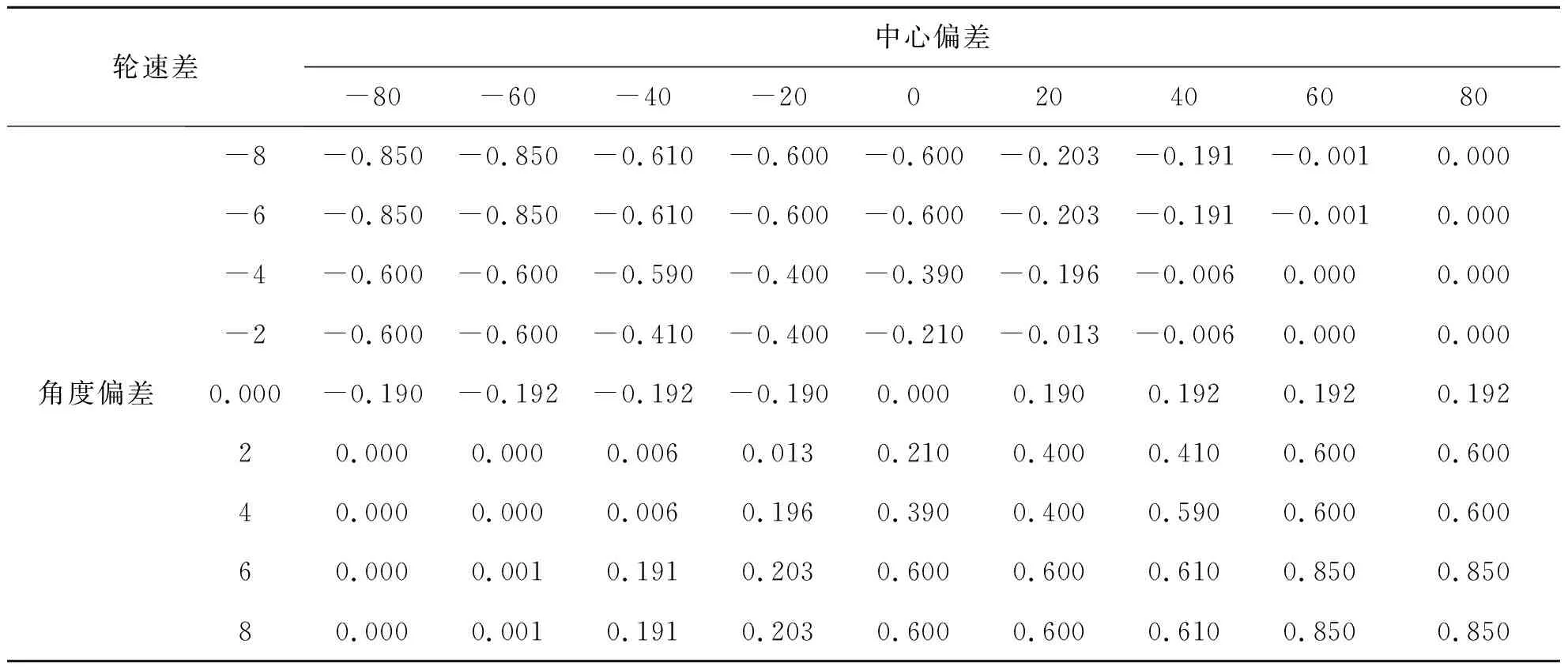
表2 控制规则观测表
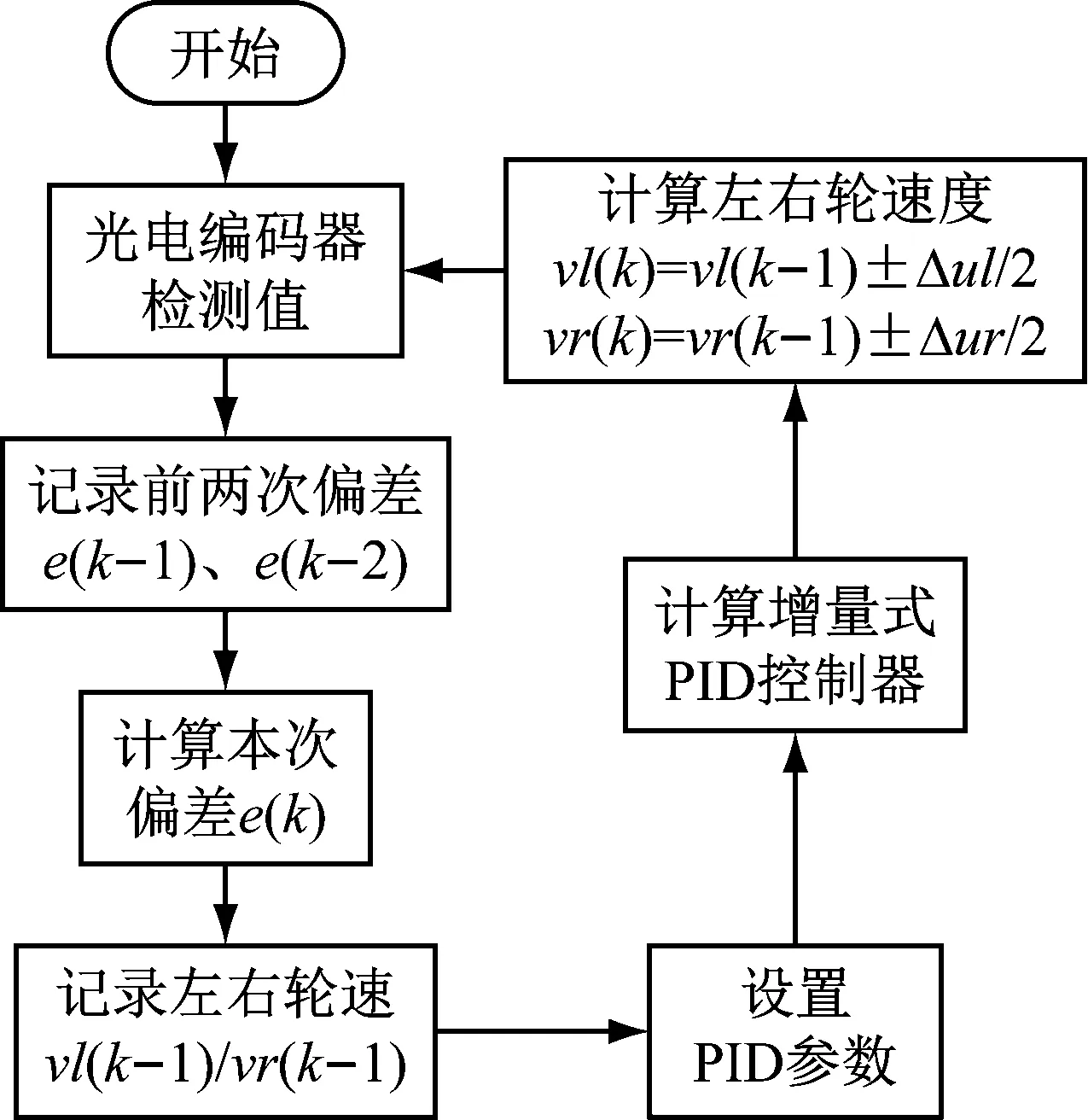
图10 PID算法控制电机转速
增量式PID公式如下:
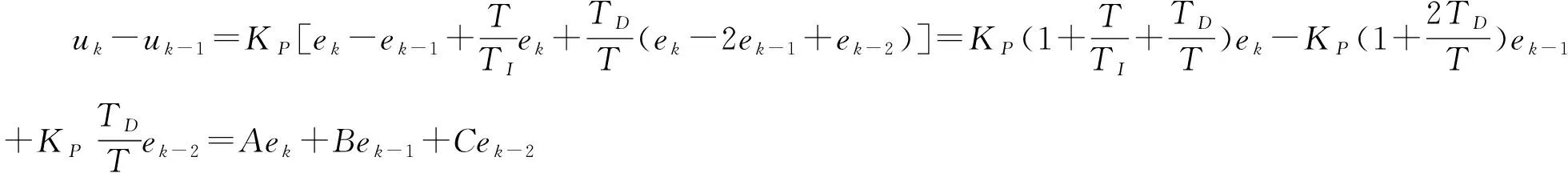
(7)
其中:
式(7)中,KP为比例系数,TI为积分时间,TD为微分时间,KP/TI为积分系数,KP/TD为微分系数。如果控制系统采样周期T固定,只需确定A、B、C,通过计算测量值与目标值的前后3次偏差,就可以求出轮速增量,从而达到闭环精准且快速地控制电机转速的目的。
精确且快速地控制电机达到期望转速,是实现模糊控制路径纠偏算法的基本要求,是移动机器人能够完成路径跟踪的保障。为了测试PID算法效果,设置实验如下:设定电机转速为5个脉冲/毫秒,检测周期为5毫秒,将目标脉冲(速度)设定值与实际脉冲检测值实时发送到上位机中监测,监测结果如图11所示。
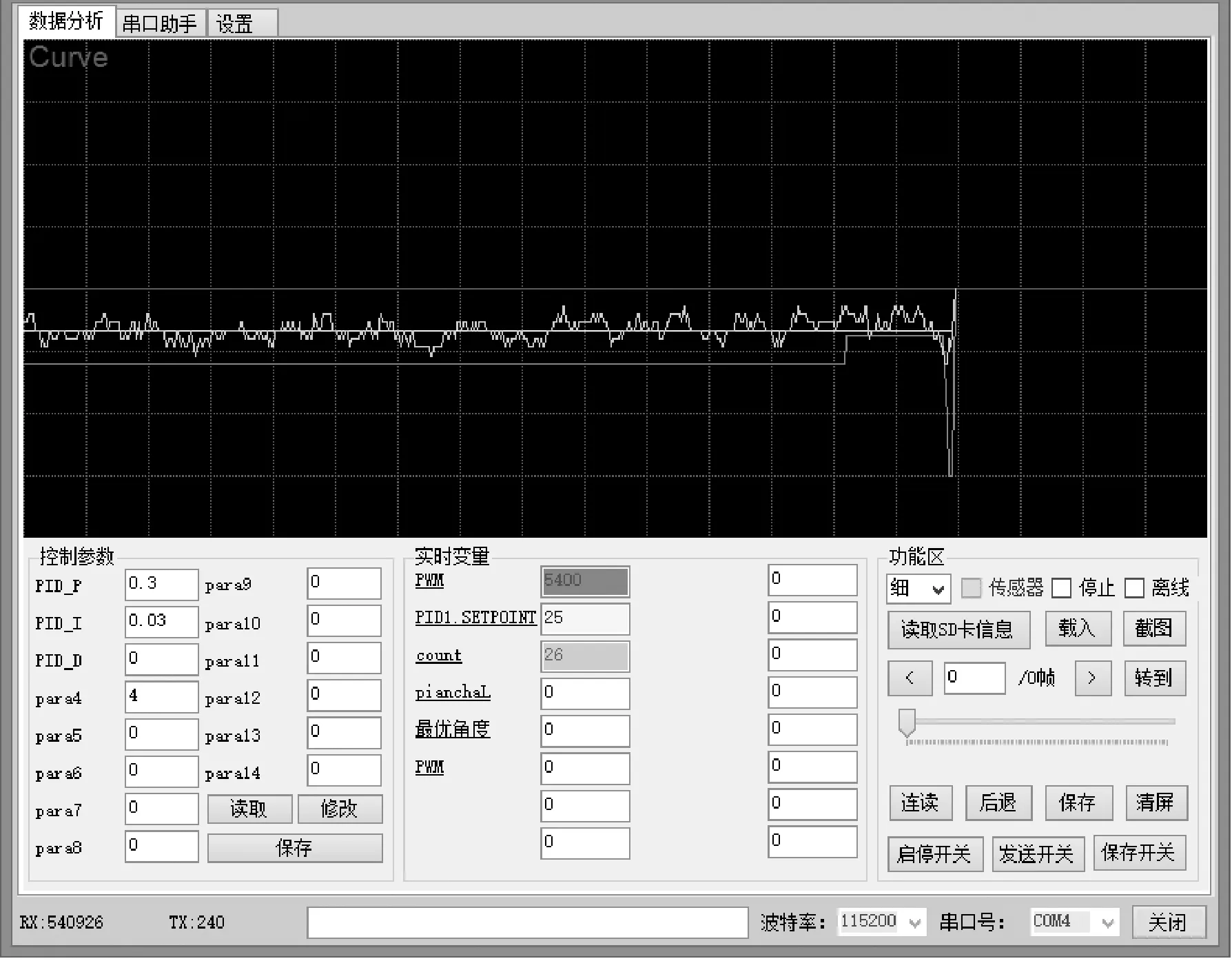
图11 速度控制实验图
图11中,中间直线为目标脉冲(速度)值,中间曲线为实际脉冲检测值,下面的折线为PWM波当前值。由图可知,当PID算法控制周期、比例系数与积分时间确定后,电机转速可精准控制在1个脉冲误差范围内,相对于电机转动一圈有8000个脉冲而言可忽略不计,可见PID算法控制电机速度效果显著。
四、结语
本文分析了组成路径跟踪系统的必要因素,包括路径纠偏、速度控制以及导航任务管理,研究了基于模糊控制算法的移动机器人路径纠偏,实现了移动机器人在非结构路面各种情况下的路径跟踪。
