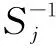关于不变测度的维数分布的一点注记
2021-01-09蔡恒超
蔡恒超
(福建师范大学 数学与信息学院,福建福州350117)
1 预备知识
为了研究一般概率测度μ及其支撑集的结构和复杂性,人们引进了所谓的局部维数:如果
其中,Br(x)表示以x为球心,r为半径的球,则称α为μ在x处的局部维数,称
为水平集.与此有关的一个由物理学家提出的著名公式是所谓的重分形公式:
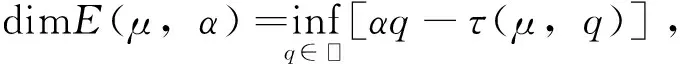
其中,dim代表豪斯多夫(Hausdorff)维数,τ(μ,q)是Lq谱,定义为

另一个考察概率测度μ及其支撑集的结构和复杂性的方法是研究μ的支撑集的维数分布.Cutler[8]考虑了μ支撑于维数不超过α的集合上的质量是怎样随着α的变化而变化的,定义了如下的维数分布:
定义1设dim(E)表示集合E的豪斯多夫维数,对于任意的α∈[0,N],定义集函数μα为
其中,B和D都是Borel集合.Cutler[8]证明了如下的结果:

这些测度μα实质上构成了概率测度μ的一个分解.利用这种分解,定义式
决定了集合[0,N]上的一个概率测度.Cutler[8]把这个测度称为测度μ的维数分布,并从 一种新的角度研究了概率测度的结构与复杂性.
一个自然的问题就是:对于由迭代函数系定义的不变测度,这种分解是否有用.本研究的目的就是回答这一问题,为此先给出迭代函数系及其不变集的定义如下:
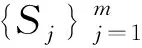
(1)
称为不变测度.
2 定理及其证明
定理设μ是(1)式定义的不变测度,μα见定义1.若Sj都是双李普希茨压缩映射(即存在大于零的实数c1 定理说明,对于由迭代函数系生成的不变测度,Cutler[8]所定义的维数分布是一个单点分布(退化分布). 证明:设α∈[0,N],使得μα不是零测度.令 其中,Sj1∘Sj2∘…∘Sjn表示n个双李普希茨压缩映射的复合,则由豪斯多夫维数的性质知道,Bα的维数不超过α.所以,由μα的定义知道 μα(B)=μ(B∩Bα) (2) 由于Sj都是双李普希茨映射,所以存在常数c>0,使得 所以,由豪斯多夫测度的性质得知 所以 对一切Borel集合B和{1,2,…,m}中的j成立. 利用概率测度μ的定义式(1)可知,对于任意的Borel集合B,由(2)式有 μα(B)=μ(B∩Bα) 由(3)式有 (4) 由于μα不是零测度.令ν=[μα(▯N)]-1μα,则ν是一个概率测度.由(4)式可得,ν满足 由μ的唯一性得知, μ=ν=[μα(▯N)]-1μα. (5) 如果μα≠μ,则μα(▯N)≠1,又因为μα(▯N)≤1,所以μα(▯N)<1.此时,μ-μα也是非零测度.令 ν′=[μ(▯N)-μα(▯N)]-1(μ-μα), 则由(1)式和(4)式得 由μ的唯一性得知, μ=ν′=[μ(▯N)-μα(▯N)]-1(μ-μα). (6) 所以,由(5)式和(6)式及(2)式得 [μα(▯N)]-1μα(Dα)=[μ(▯N)-μα(▯N)]-1[μ(Dα)-μα(Dα)] =[μ(▯N)-μα(▯N)]-1(μ(Dα)-μ(Dα))=0, 这与μα是非零测度矛盾,所以μα=μ.这说明,当μα≠0时,必有μα=μ.令 α0=inf{α≥0:μα=μ}, 则易知定理的结论(i)成立;而且α>α0时,结论(ii)成立.最后,由(3)式知道,当α=α0时,结论(ii)也成立.证毕.