球面LED阵列的光斑传输特性
2021-01-09刘沁
刘 沁
(重庆工商大学 设计艺术学院,重庆 400067)
引言
LED(发光二极管)作为一种节能、耐用的新型光源,已在各种照明环境(包括公共场所照明、家庭照明、景观照明等)中广泛地使用[1-3]。为了更加充分地发挥LED这种新型光源在照明领域的应用,从理论上对LED的照明特性进行研究显得越来越重要,并取得很多重要的研究成果。如罗晓霞等[4]对单个LED光源的大视场角准直照明问题做了研究,丁毅等[5,6]研究了单个LED光源的均匀照明问题。由于单个LED光源的亮度较小,因此绝大多数的LED光源都是由多个LED灯芯构成的阵列来实现照明的。为了在理论上弄清楚LED阵列的照明特性,我们的科研团队也开展了对这个领域的研究。我们对方形阵列和圆形阵列的照度特性做了研究[7-10], 得出了方形阵列和圆形阵列的光斑的发散规律和照度的变化规律。进而研究了圆形阵列和矩形阵列的照度均匀性[11,12],得出这两种阵列的照度均匀性的特征和变化规律。
以上对LED的阵列研究中,都是将LED阵列面固定在一个平面内。而实际的LED阵列光源多数的LED灯芯的分布是在一个曲面上。因此,研究曲面LED阵列的照明特性以及变化规律在理论上和应用上都有着非常重要的价值。球面LED阵列是在各种曲面阵列中最基本、最典型的阵列,因此在理论上弄清球面LED阵列的光斑传输特性,对应掌握曲面LED阵列的照明规律有着基础性的作用。下面以球面LED阵列为对象,引入弯曲度的概念,利用非相干光的叠加原理推导出计算球面LED阵列的照度公式、光斑半径公式以及光斑发散角公式。通过数值计算研究球面LED阵列的光斑半径随球面弯曲度的变化规律,光斑发散角随球面弯曲度的变化规律,照度峰值随球面弯曲度的变化规律。研究结果表明,球面LED阵列对光斑半径、光斑发散角以及照度都有明显的汇聚作用。利用这些特性,可以在各类场景照明中使用球面LED阵列来提高光束的方向性和照射面的亮度。
1 模型与理论
首先建立这样一个球面LED阵列模型,该球面阵列由以球面顶点为中心,在球面上作M个弧长等距的圆环,相邻圆环在球面上的弧长间隔为a。在每一圆环上都均匀分布着36个LED芯片,不同圆环上的36个LED芯片沿径向一致排列,沿X轴方向排第一列,在XOY平面内以球面顶点为圆心,每隔2π/36的圆心角方向上排一列芯片。 球面LED阵列的芯片总数为36×M。该球面LED阵列的顶点坐标在(0,0,0)处,用Aij标记其中某一芯片,其中i表示其圆心角的区别(i=0,1,…,35)、中j表示圆环的区别(j=1,2,…,M)它的坐标为(Xn,Yn,Zn),目标平面在z=h处,如图1所示。
球面LED阵列在目标平面产生照度为阵列上的每个LED芯片产生照度的非相干叠加。单个LED芯片在视角θ方向上的光强I由下式确定[7],如图2,芯片到P点的距离为l。

(1)
其中I0为0°角的光强,m值由LED芯片的产生工艺确定。
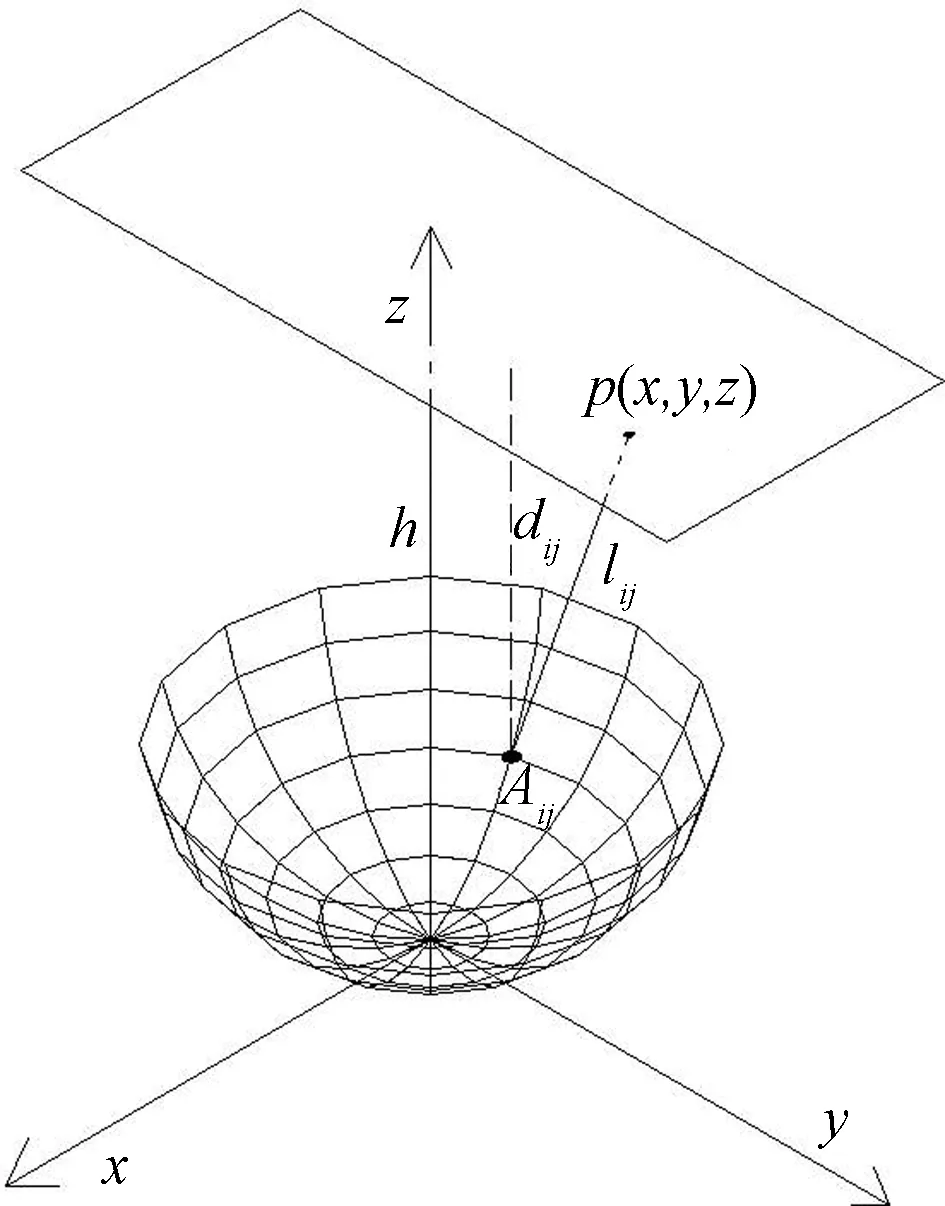
图1 球面LED阵列Fig.1 Spherical LED arrays

图2 芯片的照度Fig.2 Illuminance of LED
若芯片的坐标在(x,y,z)处,目标平面上的照明点P的坐标在(x,y,h)处,则芯片在P点处产生的照度E由下式确定[11]:
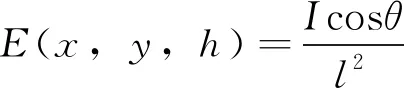
(2)
由式(1)、式(2)得到单个芯片在P点的照度为

(3)
如果阵列是由N个芯片构成的,这N个芯片发出的光彼此是非相干光,由非相干光的叠加原理阵列在P点处产生的照度为[12]

(4)
其中Xn、Yn、Zn为第n个LED芯片的坐标。
为了描述球面LED阵列的弯曲程度,需要引入弯曲度的概念。用R表示球面的半径,该球面阵列在通过球心和顶点的截面上对应的弧长为2M×a。 若取该球面LED阵列对应的弧长2M×a为圆周长的K分之一,即2Ma=2πR/K,则有

(5)
K越大R越大,阵列的弯曲程度就越小。为了能用一个与弯曲程度成正比的量来描述球面的弯曲程度,引入弯曲度D:
D=1/K
(6)
弯曲度D越大,球面弯曲程度越大,D就是描述球面弯曲程度的量。当K=,对应的弯曲度D=0,球面退化为平面。当球面阵列对应的弧长为度半个圆周长时K=2,对应的D=1/2。当球面阵列对应的弧长为一个圆周长时K=1,对应的D=1,弯曲度达到最大。对于球面LED阵列的弯曲度 0≤D≤1/2。
利用图1可得芯片Aij的三个坐标分别为

i=0,1,…,35,j=1,2,…,M
(7)
将式(7)代入式(4),可得该球面LED阵列在目标平面上的照度公式:
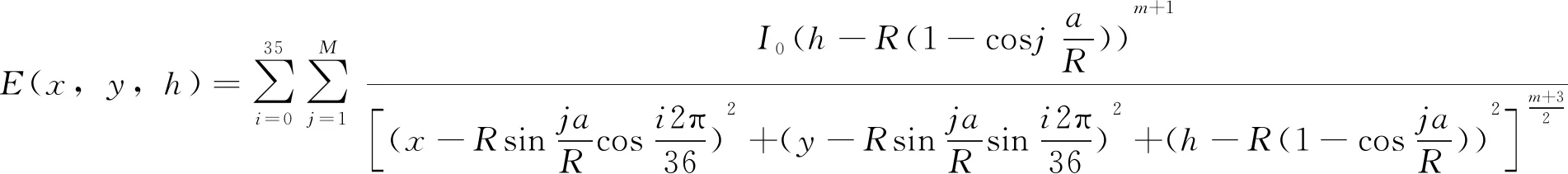
(8)
由于芯片分布的对称性,照度在X轴和Y轴上的分布Ex和Ey是相同的,可以将式(8)中的y取为0得到Ex:
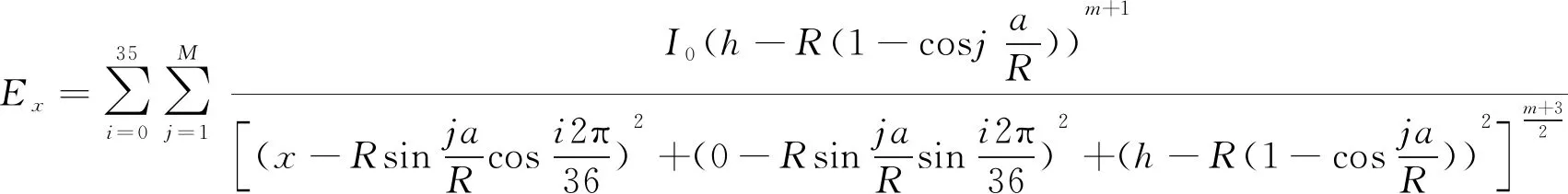
(9)
光斑中心的照度(照度峰值)为E0,可以将式(8)中的y和x取为0得到:
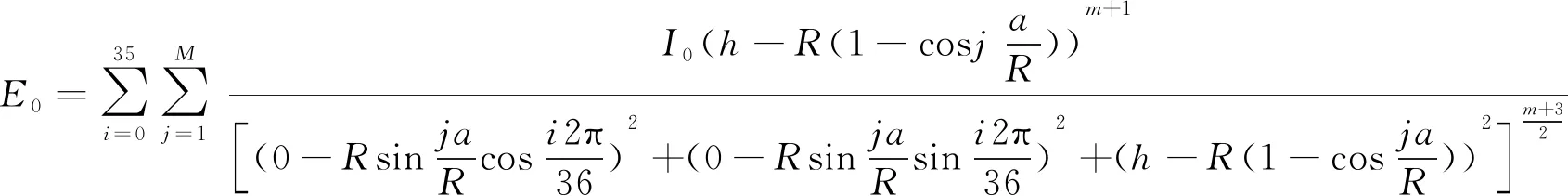
(10)
LED阵列在目标平面上形成的光斑大小由下列关系确定[11]:
E≥0.2E0
(11)
由于芯片分布的对称性,x轴和y轴上的光斑半径Rx和Ry是相同的。由式(9)和式(11)可求出Rx:
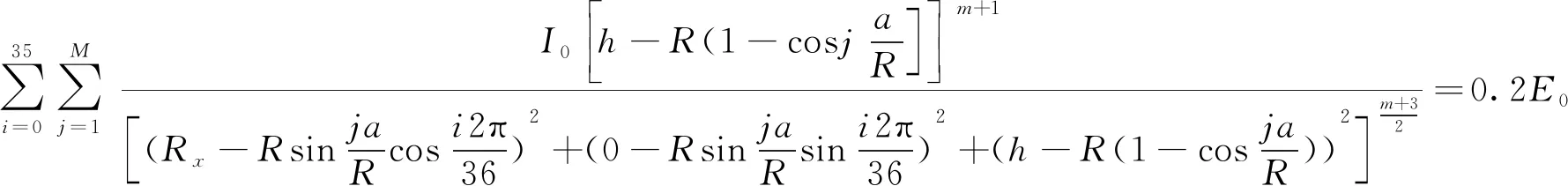
(12)
光斑的发散角φ可以由下式求得[10]:
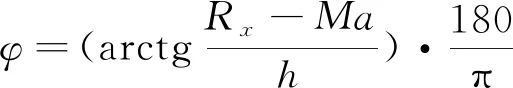
(13)
利用式(12)和式(13)可以研究该球面LED阵列的光班半径和发色角的变化特征。
2 光斑传输特性
下面利用式(5)~式(13),通过数值计算法研究球面LED阵列的光斑传输规律,即光班半径、发色角以及照度峰值随球面弯曲度的变化规律。
2.1 光斑半径随弯曲度的变化规律
固定m=5,I0=2 cd、a=0.03 m、M=40、h=4 m,研究光斑半径随弯曲度的变化关系。取K=、21、19、17、15、13、11、9、7、5十组数据,计算出对应的弯曲度D以及光斑半径Rx,见表1。

表1 光斑半径和弯曲度数据Table 1 Rxand D
由表1中的数据计算出Rx随弯曲度D的变化曲线,如图3所示。分析表1和图3可知:当弯曲度为0时对应的光斑半径Rx=2.997 m,随着弯曲度的逐渐增加对应的光斑半径逐渐减小,当弯曲度增加到0.2时对应的光斑半径减小为2.913 m。为了直观地反映光斑的变化情况,计算出K=时的光斑和K=3时的光斑,如图4所示。可知,K=时的光斑明显大于K=3时的光斑。

图3 光斑半径随弯曲度的响应曲线Fig.3 Response curves of Rx versus D
光斑半径随弯曲度的这一变化规律表明:球面LED阵列对光斑大小有汇聚的作用,弯曲度越大对光斑的汇聚效果越明显。在照明设计中,利用这一规律可以控制光斑的大小。

图4 光斑图Fig.4 Light spot
2.2 发散角随弯曲度的变化规律
仍固定m=5,I0=2 cd、a=0.03 m、M=40、h=4 m,研究光斑发散角随弯曲度的变化关系。取K=、21、19、17、15、13、11、9、7、5十组数据,计算出对应的弯曲度D以及光斑发散角φ数据,见表2。由表2中的数据计算出光斑发散角φ随弯曲度D的变化曲线,如图5所示。分析表2和图5可知,当弯曲度为0时对应的光斑发散角φ=24.197°,随着弯曲度的逐渐增加对应的光斑发散角逐渐减小,当弯曲度增加到0.2时对应的光斑发散角减小为 23.177°。光斑发散角随弯曲度的这一变化规律表明:球面LED阵列对光斑发散角也有汇聚作用,弯曲度越大对光斑发散角的汇聚效果越明显。

表2 发散角和弯曲度数据Table 2 Data of φ and D
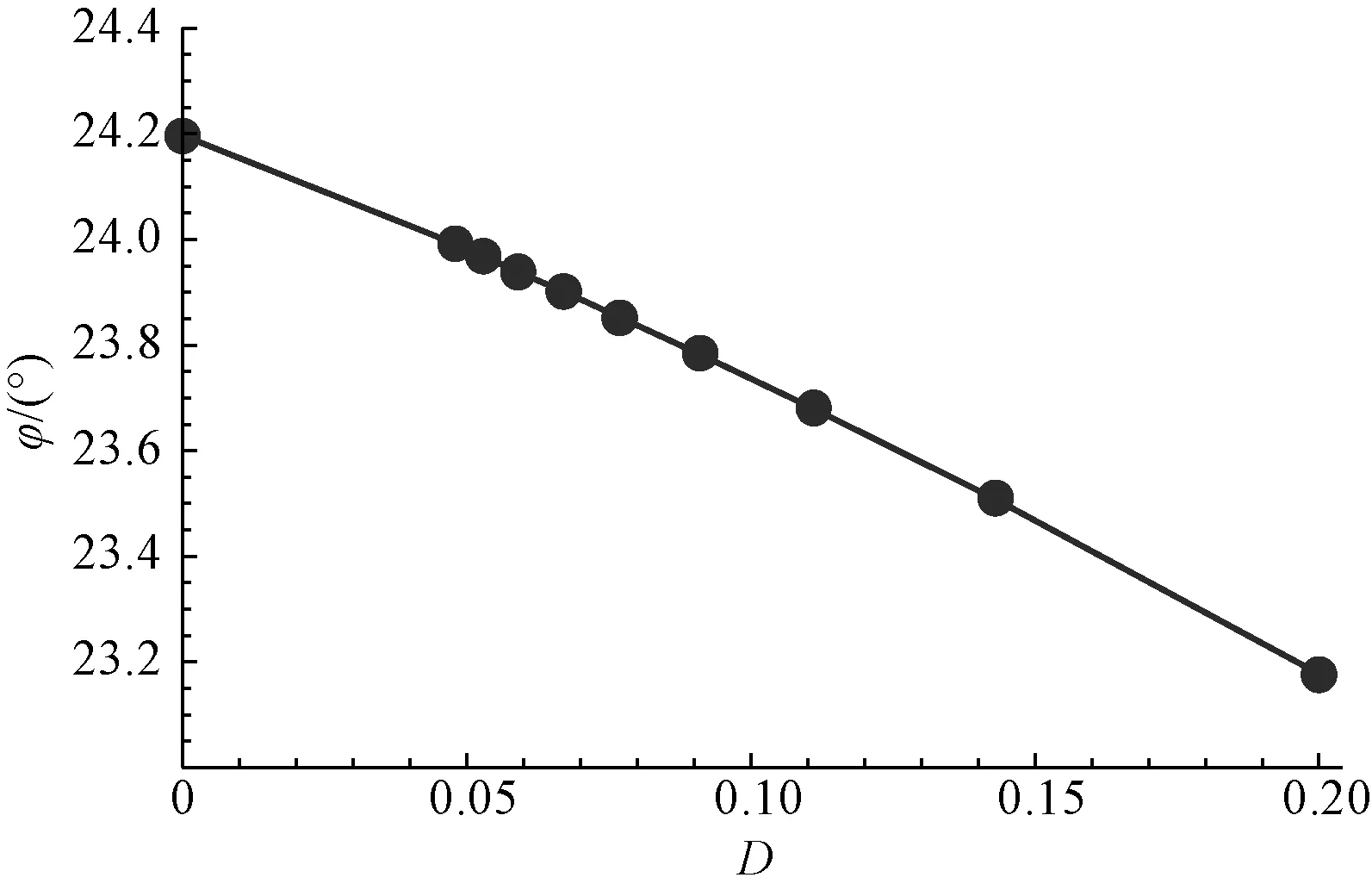
图5 发散角随弯曲度的响应曲线Fig.5 Response curves of φ versus D
2.3 照度峰值随弯曲度的变化规律
仍固定m=5,I0=2 cd、a=0.03 m、M=40、h=4 m,研究照度峰值随弯曲度的变化关系。 取K=、21、19、17、15、13、11、9、7、5十组数据,计算出对应的弯曲度D和照度峰值E0的数据,见表3。利用表3中的数据计算出照度峰值E0随弯曲度D的变化曲线,如图6所示。分析表3和图6可知:当弯曲度为0时对应的照度峰值E0=160.33 lx,随着弯曲度的逐渐增加对应的照度峰值逐渐增大,当弯曲度增加到0.2时对应的照度峰值增大为169.81 lx。照度峰值随弯曲度的这一变化规律表明:球面LED阵列对照度有聚光的作用,弯曲度越大对照度的聚光效果越明显。在照明设计中,利用这一规律可以到达提高光斑亮度的效果。

表3 弯曲度和照度峰值数据Table 3 Data of D and E0
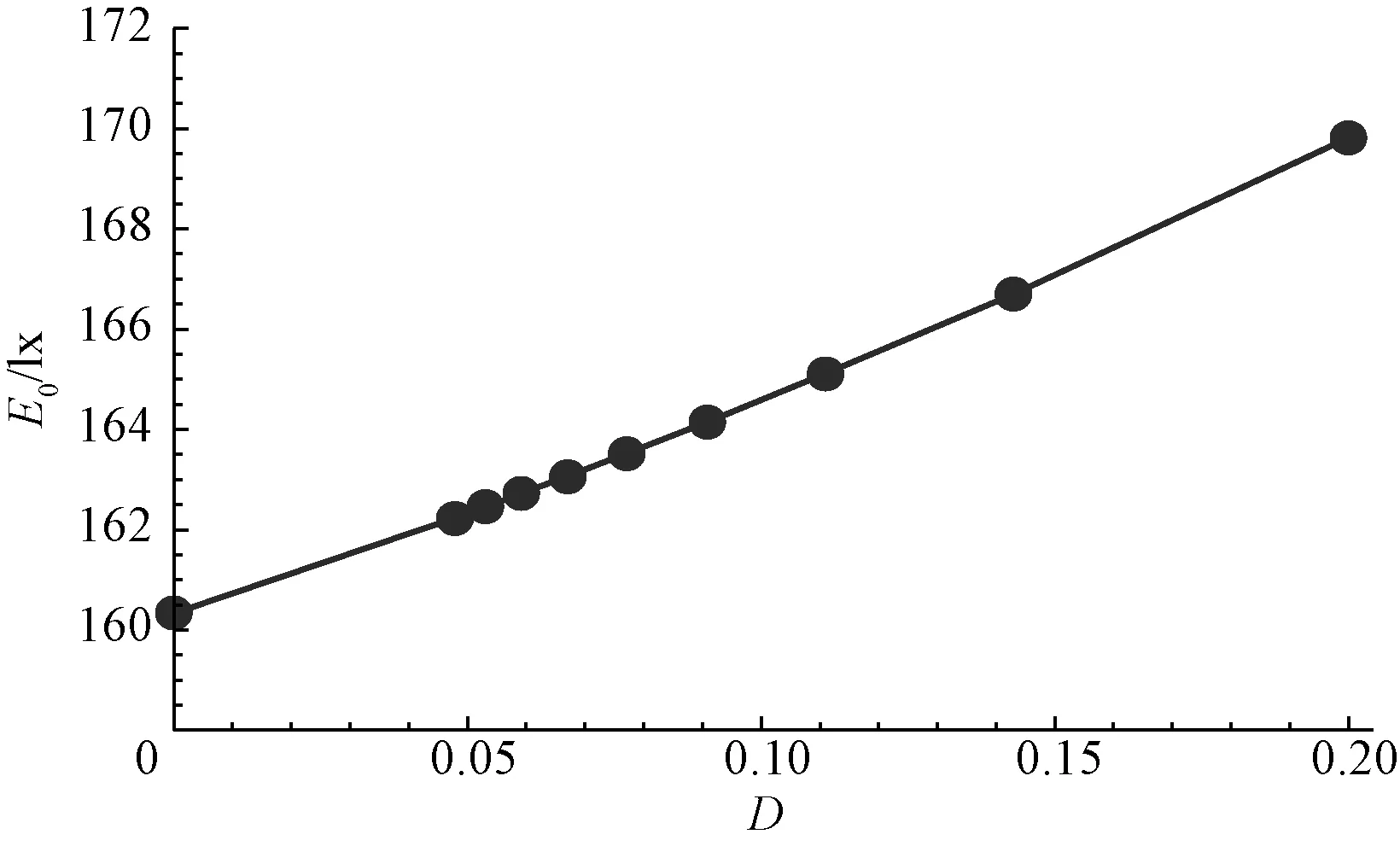
图6 照度峰值随弯曲度的响应曲线Fig.6 Response curves of E0 versus D
3 结论
本文建立了球面LED阵列的模型,引入弯曲度来描述球面阵列的弯曲程度。利用非相干光的叠加原理推导出计算球面LED阵列的光斑半径公式、光斑发散角公式和照度公式。通过数值计算研究了光斑半径随弯曲度的变化规律、发散角随弯曲度的变化规律、照度峰值随弯曲度的变化规律。计算得出:当弯曲度为0时光斑半径为2.997 m,随着弯曲度的逐渐增加光斑半径逐渐减小,当弯曲度增加到0.2时光斑半径减小为2.913 m;当弯曲度为0时光斑发散角为24.197°,随着弯曲度的逐渐增加光斑发散角逐渐减小,当弯曲度增加到0.2时光斑发散角减小为 23.177°;当弯曲度为0时照度峰值为160.33 lx,随着弯曲度的逐渐增加照度峰值逐渐增大,当弯曲度增加到0.2时照度峰值增大为169.81 lx。通过上述研究表明:球面LED阵列对光斑半径、光斑发散角以及照度都有明显的汇聚作用。利用球面LED阵列的这些特性,可以在各类场景照明中使用球面LED阵列来提高光束的方向性和照射面的亮度。
