高速铁路钢轨波磨对轮轨系统振动响应的影响分析

贾昕昱 黎国清 刘秀波

（1.中国铁道科学研究院研究生部，北京100081；2.中国铁道科学研究院集团有限公司基础设施检测研究所，北京100081）

钢轨波磨是一种发生在钢轨顶面的短波周期性不平顺，广泛存在于高速、普速、重载铁路以及城市轨道交通中。钢轨波磨会加剧车辆振动和轮轨噪声，影响乘坐舒适性，甚至会影响行车安全性［1-2］。

关于钢轨波磨特性的研究大多采用试验、仿真分析等方法。陈迅等［3］研究了地铁线路中钢轨波磨对车辆振动响应的影响，认为垂向舒适度指标不适合用于评价钢轨波磨，应提出一个更加综合的评价指标。刘玉涛［4］研究了钢轨波磨对扣件弹条的影响，分析了不同情况下弹条的受力及疲劳断裂情况。于淼［5］利用有限元模型分析了车辆通过曲线轨道时钢轨波磨对轮轨系统振动响应的影响。

本文利用ANSYS/LSDYNA软件建立了高速铁路轮轨瞬态滚动接触有限元模型，计算分析钢轨波磨对不同车速、不同轮轨摩擦因数条件下的轮轨系统振动响应的影响，为评价钢轨波磨提供参考。

1 有限元模型

1.1 模型的建立

选用中国某高速铁路的真实车轮及轨道参数，车轮踏面为LMA型，车轮直径860 mm；钢轨采用60 kg/m轨，轨底坡设置为1/40。

建模时主要考虑高频振动，而一系悬挂以上车辆部分的振动特性对轮轨高频振动影响很小，因此对一系悬挂以上部分进行简化，将车体、构架等简化为1个质量块。

建立由质量块、一系悬挂、轮对、钢轨、扣件、轨道板、砂浆层组成的轮轨瞬态滚动有限元模型。模型网格划分时采用粗、细网格相结合方式，以保证计算精度和准确性［6-7］。轮轨接触区钢轨和车轮踏面采用细网格，远离接触区的网格划分相对粗一些。列车运行时轮对横向摆动波长较长，而模型长度较短，因此不考虑车轮的横向位移影响。为减少单元数量，提高运算效率，选取车轮及轨道的一半进行分析，如图1（a）所示。高速铁路中钢轨波磨的波长通常集中于70～160 mm，波深0.02～0.06 mm。选取长度为1 m、波长为100 mm、波深为0.02 mm的波磨区段的简谐波磨施加到钢轨顶面，如图1（b）所示。

图1 有限元模型

模型中，质量块的质量取为7 000 kg；一系悬挂和扣件的刚度分别取为0.88，22.00 MN/m，阻尼分别取为4，200 kN∙s/m。扣件间距0.65 m。其他主要参数见表1。

表1 有限元模型主要参数

1.2 模型的计算过程

该模型的计算过程可以分为3个步骤：

1）应力初始化。采用隐式求解方法，计算车轮静置在轨道上时轮轨系统在重力作用下的位移。

2）动态松弛。将求得的位移场施加到相对应的节点上作为初始变形；同时在时间t=0时将平移速度和旋转速度施加到车轮上作为初始条件。

3）计算求解。计算不同条件下车轮滚过求解区时的振动响应，包括轮轨垂向力及轮轨纵向力。

2 计算结果分析

2.1 不同车速下钢轨波磨对轮轨系统振动响应的影响

计算车轮分别以速度v=200，250，300，350 km/h通过没有波磨的钢轨平顺区段以及存在波磨的不平顺区段时的轮轨垂向力和纵向力，研究不同车速下钢轨波磨对轮轨系统振动响应的影响。

车轮以不同速度通过没有波磨的钢轨平顺区段时的轮轨垂向力见图2。可知：在初始阶段，各速度级下的轮轨垂向力均存在高频振荡，而且速度越高振幅越大；随着时间的推移，振荡逐渐收敛，速度越高的收敛越慢；最终各速度级下的轮轨垂向力均进入相对稳定的状态，说明此时轮轨系统达到稳态滚动状态。

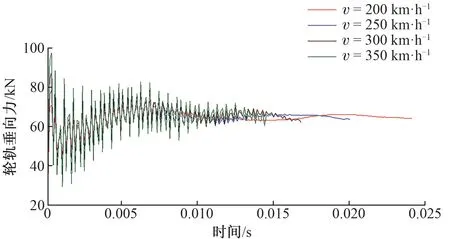
图2 车轮以不同速度通过钢轨平顺区段时的轮轨垂向力

进入稳态滚动状态后，各速度级下轮轨垂向力的高频振动幅值均保持在较小范围，此时可以进行车轮进入钢轨波磨区段的振动响应分析。

车轮以不同速度通过钢轨波磨区段时的轮轨垂向力见图3。可知：轮轨垂向力的波长与波磨的波长基本一致，轮轨垂向力的波形比波磨的波形有微小的超前，这与文献［8］的结果基本一致；轮轨垂向力的峰值随车速的增加而增大；轮轨垂向力的峰值在扣件附近为最大（对应里程约1.95 m），在两轨枕跨中附近最小（对应里程约1.65，2.25 m），且车速越高扣件对轮轨垂向力的影响越大。

图3 车轮以不同速度通过钢轨波磨区段时的轮轨垂向力

各速度级下车轮通过波磨波峰时的轮轨垂向力峰值见图4。可知：v=200 km/h时，扣件对轮轨垂向力的影响较小，扣件处的轮轨垂向力仅比两轨枕跨中大2.7 kN；v=350 km/h时，扣件对轮轨垂向力的影响较大，扣件处的轮轨垂向力比两轨枕跨中大14.1 kN。因此，车速较大时须关注扣件附近的受力状态。

图4 车轮以不同速度通过波磨波峰时的轮轨垂向力峰值

选取与原波磨幅值及频率均相同但相位相反的新波磨，计算车轮以v=300 km/h通过波磨区段时的轮轨垂向力，并与原波磨下的计算结果进行对比，见图5。可知，在2种相反相位的波磨下，轮轨垂向力的峰值均发生在扣件附近处。说明波磨的相位布置对计算结果不产生影响。

图5 波磨的相位对轮轨垂向力的影响

对车辆经过钢轨波磨区段时的轮轨垂向力进行时频分析，其中频率为200～2 000 Hz的时频图像见图6，图中颜色越亮振动能量越大。可知，v=200，250，300，350 km/h时，振动能量最大点均发生在扣件附近。因此，当车辆经过扣件时会产生较大的振动能量，加速扣件的疲劳断裂。

图6 不同速度级下轮轨垂向力振动能量时频图像

车轮以不同速度通过钢轨波磨区段时的轮轨纵向力见图7。可知，轮轨纵向力的特征与垂向力相似，其振幅峰值均随速度增加而增大，且在扣件处达到最大。

图7 车轮以不同速度通过钢轨波磨区段时的轮轨纵向力

2.2 不同轮轨摩擦因数下钢轨波磨对轮轨系统振动响应的影响

轮轨摩擦因数的变化会导致轮轨间的作用力发生变化。分别取轮轨摩擦因数λ=0.3，0.4，0.5，计算车轮以300 km/h的速度通过钢轨波磨区段时的轮轨作用力及振动加速度，见图8。

图8 不同轮轨摩擦因数下波磨对轮轨系统振动响应的影响

由图8（a）可知：①当轮轨摩擦因数由0.3增至0.5时，轮轨纵向力的振动峰值由25.13 kN增至41.31 kN。说明轮轨摩擦因数对轮轨纵向力有较大的影响。②轮轨纵向力的波形与波磨的波形基本一致。波磨波峰处的轮轨纵向力大，导致的磨损也大；波磨波谷处的轮轨纵向力小，导致的磨损也小。波峰的磨耗大于波谷的磨耗，使得波磨逐渐趋于稳定而不会无限制地发展。说明波磨区段的轮轨纵向力对波磨有一定的抑制作用。

由图8（b）和图8（c）可知，当摩擦因数改变时，轮轨垂向力及车轮轴端垂向加速度的变化都非常小。因此摩擦因数对轮轨垂向的影响可以忽略。

3 结论

为分析高速铁路中的波磨现象，本文建立了瞬态滚动接触有限元模型，研究了不同条件下钢轨波磨对轮轨系统振动响应的影响。得到以下结论：

1）车轮通过钢轨波磨区段时，轮轨作用力（垂向力和纵向力）的波长与波磨的波长基本一致，且轮轨作用力随车速的增加而增大。

2）车轮通过钢轨波磨区段时，轮轨作用力在扣件附近最大，在两轨枕跨中附近最小；车速对扣件附近轮轨作用力的影响要大于两轨枕跨中附近，车速越高扣件对轮轨作用力的影响越大；更高的车速使扣件处的振动能量增大，加速了扣件的疲劳断裂。

3）轮轨纵向力在波磨的波峰处最大，波谷处最小，且波峰的磨耗大于波谷的磨耗，这使得波磨逐渐趋于稳定而不会无限发展。

4）摩擦因数由0.3增加至0.5，轮轨纵向力随之增大；摩擦因数的改变对轮轨垂向力及车轮垂向加速度的影响很小，可以忽略。