一种工业报警相关性数据挖掘算法

杨润佳，刘泽三

1. 国家能源集团，秦皇岛发电有限责任公司，发展策划处，河北 秦皇岛 066000

2. 国网信息通信产业集团信通研究院，北京 100000

引 言

在工业生产过程中，报警系统具有至关重要的作用，其建立的目的是提高生产的安全性。但由于分布式控制系统（Distributed Control System，DCS）、实时监测系统等实时数据采集系统的建立，导致随着实时监测数据量的急剧上升，报警数据量也随之大幅度攀升，进而造成无效报警过多，报警数据泛滥，使得系统操作员工作负担不降反升[1]。文献[2]给出的国际标准是操作员每10 分钟接受的平均报警数不超过1 次，异常工况下10 分钟内的报警数不超过10 次。而对于一个普通的火力发电厂动辄则是两万多的监测点，报警数量非常庞大。若要提高安全性，除了增加操作员数量外，依托大数据技术，建立报警间相关性，减少无效报警，不失为一条有效途径。

Izadi 等[3]提出了报警系统分析、设计、管理的标准与方法，指出合理的报警系统应在漏报率、误报率、报警延迟等指标中做出平衡。Rothenberg[4]指出相关报警应该进行区别分析，为此可将报警分为序列报警与非序列报警较为合理。而对于报警的相关性分析有利于剔除无关报警，使得系统更加简洁、有效地展示报警信息，同时有助于操作员在此基础上分析报警原因，进行异常工况预测。Choi 等[5]则提出了一种针对二元序列的相似度计算方法，并指出可以利用凝聚层次聚类算法对报警数据进行分组。凝聚层次算法中最为关键的是相似度算法，因此有的研究者对现有的相似度函数进行总结归纳，提出了各种针对相似度函数性能的不同的评价标准[6-8]，并指出可以使用互相关函数算法作为计算报警相似度的度量方法[9]。报警聚类是报警相关性分析的前提。有了报警类，才能分析报警类之间的相关性。在报警相关性度量方面，文献[10,12]都提出了一种针对非规整报警的相关性的量化分析方法——以概率形式表示相关性大小。

近年来，由于信息技术，尤其是大数据技术的发展，不同学者针对在不同领域的报警之间缺乏联系，容易引发次生灾害的问题，分别提出了各种基于数据分析的报警间关联关系的数据挖掘算法。该研究方法已经成为了近年来报警研究的重点内容之一，很值得进一步深入研究[6,12-17]。

但是，我们研究发现，现有的方法几乎都是将报警数据做分类假定，之后研究出针对假定条件的分析相关性的方法。比如，假定研究的报警数据是规整报警，或者假定报警数据是非规整报警，又或者假定报警数据是序列报警，或只针对非序列报警。而现实情况下，我们很难预先得知所研究的系统报警数据到底属于哪一类，是否符合假定条件。文献[10]针对报警问题指出：报警类之间的影响是有方向性的，或者说相关性应该是有矢量关系。比如，现实中A 类报警的发生会导致B 类报警的发生，即报警A 和报警B 之间在时间维度上存在着严格的“先后”关联关系。A 类报警与B 类报警之间有相关性，但是B 类报警的发生不一定是A 类报警引起的，也可能是其它条件触发的，因此A 类报警对B 类报警的影响未必等同于B 类报警对A 类报警的影响。

为了研究类似于上述的两个报警类在时间维度上的关联关系，本文在改进后的传统凝聚层聚类算法的基础上，完成报警聚类；利用大数据分析方法，提出了一种不需对报警数据做类别假定的相关性量化分析算法，并在时间维度上定义了报警的矢量性，全面挖掘并展示报警的相关性。最后，利用某电厂的实际数据进行测试，证明该方法行之有效。

1 报警聚类算法

1.1 报警数据特点

在实际工业生产中，每个测点会设置不同的报警上下限阈值，当点位实际测得的值超过设置的阈值时，就会产生相应报警数据。因此，报警数据与测点设置的阈值有关。

一般情况下，随着工业系统的投运，报警数据会随着工业系统运行而累积，报警数据量十分庞大。

工业报警数据具有如下特点：

(1) 工业系统具有相对的独立性和完整性。一般情况下，工业系统追求稳定，一段时间内不会发生较大的实质性变化，因此报警数据可认为是该段时间内工业系统在某些特性方面的反应。

(2) 报警数据量庞大。随着系统的投运，系统会累积大量报警数据，而且运行越久，数据量越大。

(3) 报警的发生具有一定的随机性。报警数据在时间上是不定期出现的，具有随机性。对于那些定期发生的报警，是极其罕见的。如果报警真的是定期出现，那么该报警肯定会被操作员觉察，进而消除。即使限于条件，未能消除，也会有充足的时间做好预警。因此，此类报警研究价值十分有限。

(4) 对于一个相对稳定运行的工业系统，报警类型是有限的，即报警数据所反应的报警类型具有有限性。可按报警的属性（测点、报警类型等）进行类别划分，或按某种聚类算法进行聚类，可得到有限数量的报警类型。

当然，随着系统的投运，投运设备的更新，新类型的报警会产生，此时需要重新进行聚类。

报警聚类是进行报警相关性分析的前提，只有建立报警分类后，才能对报警类之间的相关性做进一步的分析。

1.2 改进型凝聚层次聚类算法

凝聚层次聚类算法，是一种相对简单且有效的分类算法。利用该算法针对工业报警特性进行改进，进而得到有研究价值的报警类，是可行的。

首先，我们需要分析下工业报警在时间维度上的序列特点。

1.2.1 报警状态序列

图1 过程变量及报警阈值Fig.1 Process variable and the alarm trip points

图1 是一个典型的工业测点报警示意图。用“0”表示正常状态，“1”表示报警状态（包括高报警限与低报警限）。以超出上限为例，报警序列为高报警阈值为则报警序列可表示为：

为了规避连续重复报警现象（误报的一种），需将报警由正常变为超限的时刻记为“1”，其余均记为“0”。

序列化可得到测点的报警状态，并使之数量化，为后续聚类做好准备。这种序列化可以很好地对不同测点的不同状态做出识别，但是并没有对同一测点的报警类型做进一步区分，比如即使是同一个测点，低报和高报是不同的，而且这种不同对与该测点相关的其它测点产生的影响也是不同的，很可能影响我们要研究的报警相关性。因此，需要在凝聚层次聚类之前依据报警类型的不同做出标识。

1.2.2 基于权重的多态报警序列

为了将不同测点、不同报警作区分，可借鉴生物学碱基对标识基因序列的形式，将报警类型做纵向分类，设置不同的标识。如此，每个测点即可形成自己的类“基因”时序序列。

为了便于后续聚类运行，这种标识建议设置成数字。例如：可将纵向报警分类为：低低报警、低报警、正常值、高报、高高报（种类可依据实际情况做增删），对应报警阈值为对应数字标识表示为：-2、-1、0、1、2。其中，数值表征报警严重程度，正负号表征报警方向。则上述序列化公式可优化为带权重的序列化公式：

1.2.3 传统的凝聚层次聚类算法

Choi 等[7]提出了针对二元序列之间的相似度计算方法，进而利用凝聚层次聚类算法进行分类的算法。

凝聚层次聚类算法是一个相对简单的聚类算法，具有相对广泛的性实用与适用性，并且自诞生那一刻开始就在不断的演进[11]。算法的关键是相似度如何进行计算。

Yang 等[11]指出，针对报警系统性能最好的相似度函数为Jaccard 函数与Sorgenfrei 函数。其中，Jaccard 函数的形式为：

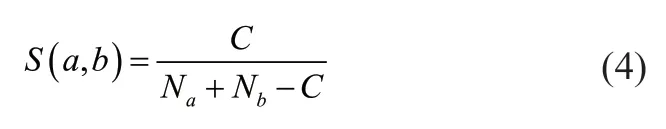
Sorgenfrei 函数的形式为：

式中，S表示序列a 和序列b 的相似度大小；其中Na为序列a 中出现报警，即数字“1”的个数，Nb为序列b 中出现报警，即数字“1”的个数，而C则表示两个序列中相同位置出现报警时，即同时出现“1”的个数。

因此，有上述公式（4）和公式（5）可知，在Na、Nb不变的情况下，C的值越大，相似度S的值越大，也就是两个序列中同时出现报警越多，相似度越大。

为处理序列报警可能存在的整体延迟，可以对序列a 进行时间长度为τ 的整体平移，用平移得到的新序列aτ与b 计算相似度S，并选取不同的τ 多次计算以使S值最大，即：

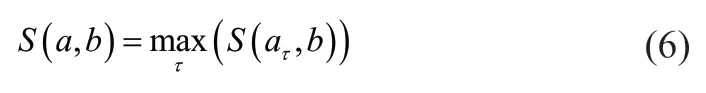
上述算法是针对规整报警的，但在实际生产过程中，经常会出现延迟时间不固定和非对称的非规整报警。针对非规整报警，在0、1 序列化的基础上以概率的形式给出了一种简易可行的相似度算法：

(1) 计算序列a 中“1”的数量，记为N；

(2) 设定窗口长度L；

(3) 对于序列a 中的每一个“1”，若在序列b 对应位置前后各为L 的长度内存在一个“1”，则记为一个“A1”，将序列a 中“A1”的数量记为m；

(4) 则可得序列b 相对于序列a 的相关性S(a,b)=m/N ；

(5) 同样的方法可计算序列a 对序列b 的相关性。

示例如下图2 所示，Pn为所选取的点位，取L=1，可得m=2，序列b 对序列a 的相关性S=2/3=0.66。

图2 相关性计算示例Fig.2 Example for correlation computation

1.2.4 改进后的凝聚层次聚类算法

上述几种凝聚层次聚类算法，无论是传统的针对有固定延时的固定序列形式的Jaccard 函数与Sorgenfrei 函数，还是针对非规整报警的，都是基于一种假设，即事先假定所研究的报警是有固定延时的规整报警，或是非规整报警。这种假定有其合理性，事先熟知所研究的对象系统，且对其中的报警关联关系有一定程度的感知。但是，有很多情况是对所研究对象的内在关系不很熟悉，更多情况是需要从无到有，挖掘出报警间的相关性。此时，往往是只知道所研究的报警数据（当今大数据挖掘既是如此）能得到报警序列，序列是否是固定延时关系，是否是规整的，都不得而知。另外，上述几种方法都没有体现出报警在时间序列上的矢量关联关系，更没有体现出报警不同状态（高报、高高报等）下的高粒度影响。

因此，本文在多态报警序列的基础上，提出了一种基于权重的多态时序通用型相似度算法，该方法如下：

(1)统计报警序列a 中非零的状态，并按权值排序，形成序列a 的报警状态集合S={S1,S2,…,SN}，Sn为序列的一个报警状态；

(2)若集合S 为空，则算法结束，否则从集合S中选取某一报警状态Sn(1 ≤n≤N)，同时从集合中去除Sn；

(3)计算序列a 中Sn的数量，记为N；

(4)设定时序窗口长度τ；

(5)对于序列a 中的每一个状态Sn，若在序列b对应时序位置后τ 的长度内存在一个非零状态，则记为一个“Tag_A1”，将序列a 中“Tag_A1”的数量记为m；

(6)则可得序列b 相对于序列a 的Sn报警状态的相关性Rn(a,b)=m/N；

(7)将Sn加入到序列a 的多态相关性集合R(a,b)；

(8) 重复步骤(2)～步骤(7)，直至集合S 为空，可得序列a 的多态相关性集合R(a,b)={R1,R2,…,RN}；

(9) 去除多态相关性集合R(a,b)中数值小于规定相关性阈值Rthreshold，新的集合R(a,b)={R1,R2,…,RM}中剩余的元素就是序列a 相对于序列b 相关性的多态聚类结果集。

计算示例如下图3 所示，取时间窗口长度τ=3，依据上述算法可得序列a 的状态集合S={-2,-1,1,2},相关性R(a,b)={0.5,0,0.67, 0.5}, 若取相关性阈值Rthreshold=0.6，则可得序列a 相对于序列b 的相关性聚类是序列a 标识为1 的一类（其它忽略）。

上述示例中，会发现一个极为不合理的现象，低低报的相关度为0.5，而低报的相关度为0，这与常识“发生低低报时肯定会发生低报”相违背，即多态序列的状态有“包含”关系，因此可将上述算法借助于“基于权重的多态报警序列”中的权重值做进一步优化。

上述算法的步骤(3)和步骤(5)需要做如下优化：

(3) 优化为：计算序列a 中与状态Sn同向且权值不小于Sn的非零的状态数，记为N；

(5) 优化为：对于序列a 中的每一个报警方向与Sn同向且权值不小于Sn的，若在序列b 对应时序位置后τ 的长度内存在一个非零状态，则记为一个“Tag_A1”，将序列a 中“Tag_A1”的数量记为m。

优化后，上述示例的相关性集合R(a,b)={0.5, 0.67,0.6,0.5}，若取相关性阈值Rthreshold=0.6，则可得序列a 相对于序列b 的相关性聚类是序列a 标识为-1，1 的两类。

图3 多态时序相关性聚类方法示例图Fig.3 Example for correlation computation based on multi-alarm-state sequence

通过上述基于权重的多态时序通用型相似度算法，我们可以很明显的发现，相较于传统方法，该方法将工业报警按照以权重为依据进行了轻重缓急式的划分，相较于传统方法的粗放式区分，更加明细清晰，便于后续以此为基础进行报警管理；以权重表示的报警的重要程度，数字化报警级别，可以进一步精细化报警管理。

2 报警类矢量相关性挖掘算法

2.1 报警相关性的矢量描述

本文所提及的报警相关性是指在某个运行的系统中，某一类报警发生对另一类报警发生产生的影响。若报警A 的发生，在一定程度上会引发报警B的发生，则称报警A 与报警B 相关；反之，若报警A 的发生与报警B 的发生毫无关联，则称报警A 与报警B 无关。

显然，在实际的工业系统中报警A 对报警B 的影响（或称报警A 与报警B 相关）不一定与报警B对报警A 的影响相同，即两个报警之间的影响是不对称的，具有方向性，本文称这种方向性为两个报警相关的矢量性。

如何度量这种报警矢量相关性的大小较为合适，对后续从数据中查找和表示这种矢量相关性至为重要。经研究发现，很多研究者都采用概率的形式作为相关性度量的形式[10,12,19-20]，本文认为借鉴条件概率形式表达这种矢量相关性较为合适。

当报警A 发生时，可用报警B 发生的概率P(B|A)来表示报警A 对报警B 矢量相关性的大小，进行度量。当报警A 发生时，报警B 发生的概率越大，则视为B 与A 的矢量相关性越强，反之则A 与B 的相关性越弱。在系统运行的相当长的时间内，在报警A 发生时，报警B 就没有发生过（或极少发生）时，即B 发生的概率P(B|A)≈0，则称报警B 与A 无关。显然，报警B 与报警A 的矢量相关性不一定等于报警A 与报警B 的矢量相关性，即P(B|A)不一定等于P(A|B)。

2.2 报警类相关性的获取算法

在工业系统运行一段时间后，会产生大量的报警数据，如何从这些报警数据中获取报警之间的相关性，对于报警的预防管理和安全生产都具有十分重要的意义。

为了找出这种矢量相关性，我们首先需要获取系统运行相当长时间内的报警数据；然后借助上一章的聚类算法，从系统的报警数据中聚类出报警类；之后在获取的报警类的基础上，才能研究报警类之间的矢量相关性；最后借助挖掘出来的相关性为生产服务。

当下几乎所有的工业系统几乎都安装了DCS 系统等工业运行系统，可以十分便利的获得相当丰富的大量报警数据。从这些数据中，利用上一章阐述的基于权重的多态时序通用型相似度算法的改进型凝聚层次聚类算法，不难获得报警类。因此，以下主要阐述在获得的报警类的基础上，如何挖掘报警类之间的矢量相关性。

从上一节报警矢量相关性的定义，不难发现找出这种关系不难，但是确认这种相关性却是比较困难。

理论上，在某一类报警发生后，系统后续一段时间内（以下简称这段时间为时间阀）发生的所有报警都有可能与之相关。当某类报警发生时，在与之相关性的报警中，有些报警经常会发生（强相关，这类相互关联的报警往往已经被标识为报警联动，随着系统的投运，很容易被运行人员察觉），有些可能偶尔发生（弱相关，可能触发条件不充分，或与之无关），甚至有些实际上无关的报警，也恰巧发生了。因此，如何甄别与该类报警相关的所有报警类，将显得至关重要。

从报警矢量相关性的定义可知，与报警A 相关的报警应该是在报警A 发生后发生的报警，因此可用时间序列拓扑图进行描述，如下图4 所示。

图4 与某类报警A 相关的报警类分布示意图Fig.4 Sketch map of the correlation between alarm A and others

图中原点表示某类报警A；实心圆点表示与报警A 相关的点；空心圆点表示与报警A 无关的点；横轴表示时间距离t；圆点与原点A 之间的距离表示报警A 发生后，该点代表的报警类与报警A 发生时的时间维度上的欧氏距离。

理论上，当选取恰当的时间间隔T 后，即可涵盖与报警A 相关的所有报警类。

假定时间间隔T 已知后，可按如下算法获取报警A 的矢量相关报警集合CA（与报警A 相关的报警类组成的集合）：

(1)从大量的报警数据中获取报警A 发生的集合CAt=(Ati|i=1,2,3,...,N)，Ati表示在ti时刻A 类报警发生了一次；

(2)创建与报警A 存在矢量相关性的报警集合CA=Ø，及相对应的关联报警发生次数集合Ccount=Ø；

(3)若集合CAt=Ø，则跳转到步骤(8)；否则，选取集合CAt中第一个元素At1，即报警A 在t1时刻发生的报警实例；

(4)从报警数据中查询得到t1时刻到t1+T 时刻发生的所有的报警集合Calarm={a1,a2,...an,且ai≠aj, 1 ≤i≤n,1 ≤j≤n,i≠j}；约定：若从t1时刻到t1+T 时刻某报警ai重复发生多次，即报警发生次数≥2，则只记录一次；若从t1时刻到t1+T 时刻之间报警A 又发生了，则只统计报警A 两次发生之间的报警；

(5)若集合Calarm为空，则从集合CAt中去掉元素At1，之后跳转至步骤(3)；否则，从集合Calarm中选取第一个元素a1；

(6)查询报警a1是否在矢量相关集合CA中。若不在，则将报警加入到集合CA中，同时在计数集合Ccount中追加一个新元素1；否则，查询报警a1在集合中CA的位置i，并将集合Ccount中的第i 个元素ci加1；

(7)从集合Calarm中去掉a1，跳转到步骤(5)；

(8)若集合Ccount不为空，则可统计与报警A 相关报警的相关度。依次计算集合Calarm中每个报警元素 ai在报警A 发生时出现的概率P(ai|A)，100%(1 ≤i≤n,ciCcount,N是集合CAt的度)，由P(ai|A) 构成新的报警A 相关度集合PA；

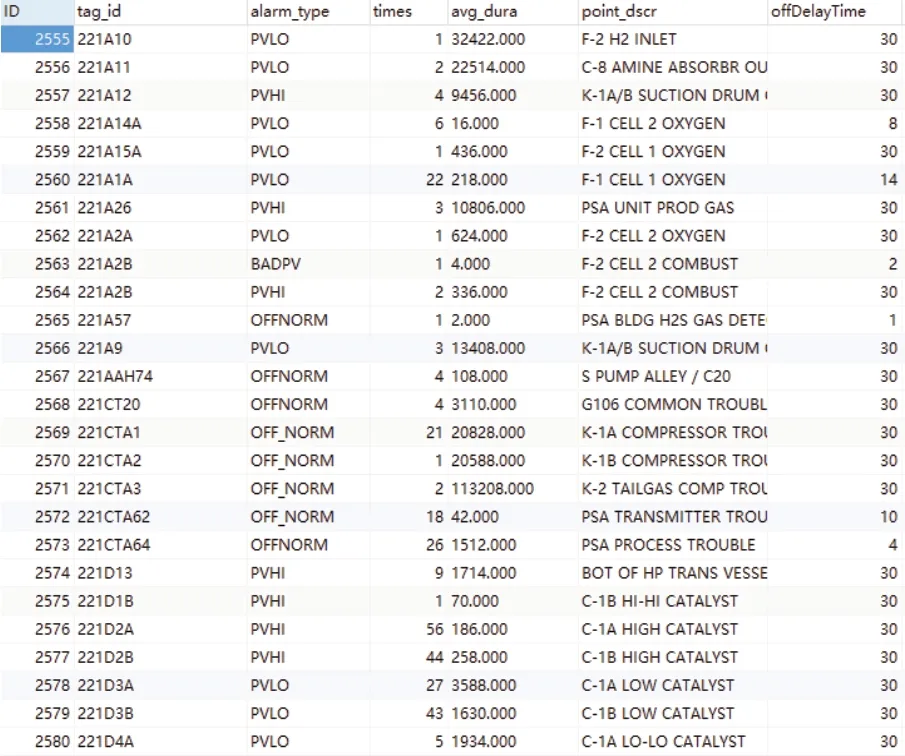
(9)相关度校正。若集合PA≠ Ø，则可选取合适的经验值Ps(0 ≤Ps<1)，去除集合PA中元素值Pi

(10) 若Calarm≠ Ø，则 集 合PA≠ Ø（集 合PA与Calarm同步，且元素一一对应），集合Calarm即为与报警A 矢量相关的报警集合，集合PA为与集合Calarm中元素一一对应的报警矢量相关度。

2.3 时间阈值T

不难理解，上节算法中提及的时间阈值的含义是：报警发生后，它的影响在时间上能传递“多远”。

时间阈值的选取，将直接关系到报警分析模型的时效性与准确性。

很明显，对于一个连续运行的系统，选取不同的时间间隔（时间阀），与某一类报警相关的后续报警类数目变化很大。理论上时间阈值越小，相关报警数据量将减少，计算量越小，时效性越好；时间阈值越大，相关报警数据量越多，计算量越大，时效性越差；而且，每类报警的时间阈值应该是不同的。

一般情况下，可根据报警的具体情况，依据经验进行设定。在一个稳定运行一段时间的系统，某类报警发生时，它的影响能传递多远，是可以依据系统特性以及运行管理人员的经验获取得到的。

当然，若没有恰当的经验值可供参考，可按如下两个公式选取时间阈值T：

公式(7)时间阈值T 的计算是基于如下假定：假定报警A 连续前后两次发生的间隔内，与之相关的报警应该是发生的；而公式(8)时间阈值T的计算是则是假定相关报警不一定发生，以大量计算作为代价，获得尽可能穷尽相关报警为目标。

2.4 报警相关度校正值Ps

应用上面的算法，从报警大数据中可计算获取的某类报警类的矢量相关报警，尽管已经利用“时间阈值”做了过滤，但是经试验数据检验（参见下章“案例研究”），发现数量还是不少。如果相关报警数量过多，可能会影响在运行中应用的时效性和准确性，所以需要依据相关度校正值Ps对做进一步取舍。

如果我们获取了足够多的数据量，可以做如下假设：在某类报警发生时，若与之相关的报警出现的条件概率极低，则可假设该相关报警是偶然发生的，与该报警无关，可以忽略。即使事实上是相关的，鉴于从历史数据上分析得到发生的概率极低，也可视为无关。

算法中用来取舍的报警相关度校正值Ps至关重要。从某种意义上来看，校正值Ps是反应与报警A相关的所有报警中运行系统所关注的相关程度，或者说是报警A 的重要程度。若Ps选取较大的值，则是关注与报警A 相关性较大报警，属粗放型，显示报警A 关联面不是很大；反之，则是关注与报警A 相关性尽可能多的报警，细致入微，显示报警A 关联面可能很广。

3 案例研究

3.1 数据

本文选取某火电厂2014年1月至2014年8月的14 万余条报警数据，采用上述算法进行了试验。部分数据样本如下表1 所示。

表1 部分数据样本列表Table 1 Part of test data

3.2 算法在实验数据上的应用

在我们获得工业报警数据后，可针对这些数据采用上述方法进行测试实验，挖掘报警之间的相关关系。

3.2.1 报警聚类

采用“基于权重的多态时序通用型相似度算法”，依据测点ID、报警类型和优先级，其中优先级选取低低报警（-2）、低报警（-1）、高报（1）和高高报（2），从给定的数据集中进行聚类分析，可得到该数据集的报警类。聚类结果详见表2。

相较于传统报警聚类，只做报警ID 和报警与否的分类，将会得到更详尽而精确的报警结果。如此，将更有利于下一步的分析——查找报警之间的相关性。

3.2.2 报警相关性分析

利用报警相关性获取算法，依次查找每个报警类的相关报警；矢量性依据报警在时间上发生的先后关系来定。

时间阈值T 取公式（7）的值。

报警相关度校正值Ps取60%，结果如下表3 所示。

3.3 算法计算结果

3.3.1 报警聚类结果

应用上述“基于权重的多态时序通用型相似度算法”的改进型凝聚层次聚类算法，得到的报警类部分结果如下表2 所示。

表2 报警聚类结果列表Table 2 Result of alarm cluster

3.3.2 报警矢量相关性结果

采用上述算法，分析得到的部分报警矢量相关结果如下表3 所示。

表3 中只列出了报警发生次数在10 次以上，相关度大于60%的数据，即报警相关度校正值Ps取60%。之所以选择报警次数多余10 次的数据，是因为考虑到在大量报警数据中，只发生过几次的报警不具有统计性。

表3 报警矢量相关结果列表Table 3 Result of alarm vector correlation

图5 报警矢量相关性的二维矩阵展示图Fig.5 Representation of alarm vector correlation with two-dimensional matrix

3.4 报警矢量相关性结果的二维矩阵展示

报警矢量相关性展示可以是图形、列表等多种方式，都可以展示某一类报警和与其相关的其它报警之间的关联关系。

表3 以列表的方式对报警矢量相关性进行了展示，但是很明显，列表这种罗列的展示方式在矢量相关性的方向性特点的展示上明显不足。为了更准确、直观反映报警之间的矢量关联关系，可借助二维矩阵进行展示。

二维矩阵展示报警类之间的矢量关联关系的规则如下：用二维矩阵行和列表示报警类集合中的元素；矩阵中的数值表示行对应的报警类和列对应的报警类之间的关联度（条件概率），即矩阵中的某个值表示该值所在行对应的报警类发生后，所在列所对应的报警类有多大概率会发生。若值为0，表示无关；矩阵主对角线的值是100，即表示报警类对自己本身的影响是100%。

由上述二维矩阵建立规则可知，所建立的二维矩阵应该是一个非对称矩阵，可以很好地表达报警类之间的矢量关联关系。

上述实验结果的二维矩阵展示如图5 所示。

4 结论

本文依据工业报警数据的时序特性和报警特点，在传统二元序列的基础上，首次提出了基于权重的多态时序通用型相似度算法，改进了传统的凝聚层次聚类算法。同时，首次提出了报警矢量相关性的概念，并指出采用条件概率形式既可恰当表述矢量相关性的大小，又可以表示其方向性；而且在上述基础上，提出了一种针对大批量报警数据的挖掘报警类之间矢量相关性的算法。

该方法为时间序列报警间关联关系的挖掘提供了量化分析依据。

经生产数据试验表明，该算法确有实效。文中最后还对报警矢量相关性的表示进行了探讨，提出了借助二维矩阵形式可以直观展示此种关联关系。

利益冲突声明

所有作者声明不存在利益冲突关系。