多目标粒子群算法的影响因素及改进策略

鲁欣欣　王淮冬

摘 要：粒子群算法独特的運算结构和出色的收敛速度被用于各行各业解决优化问题。如今生产模式智能化的速度加快，单目标的粒子群算法已经无法满足各行业对算法优化的需求，粒子群算法的多目标优化应运而生，通过对算法改进实现了粒子群算法解决多目标优化问题，但解决多目标优化的同时，影响粒子群算法的因素也增多了。文章重点介绍了多目标粒子群算法的影响因素和改进策略。

关键词：粒子群算法;多目标;改进策略

0   引言

多目标粒子群算法在解决多变量的优化问题时也加大了算法本身的运算难度，并且影响运算结果的因素也多于单目标粒子群算法。本文主要对多目标粒子群算法的影响因素进行研究阐述，并介绍改进办法。对多目标粒子群算法运算中遇到主要问题进行分析，并介绍几种解决算法问题的方法和途径。

1 基本粒子群算法

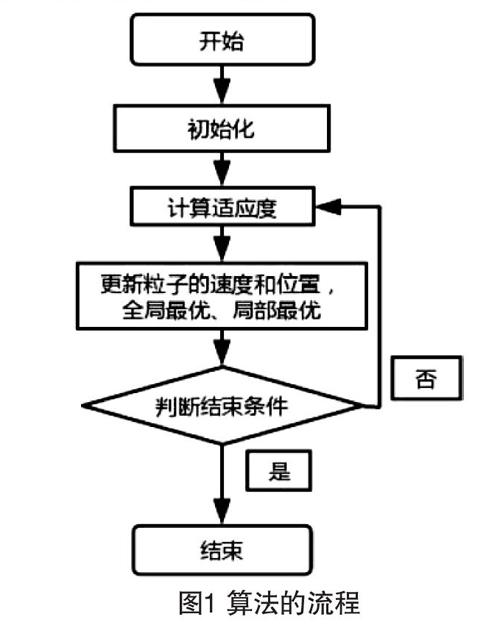
PSO基于群体的随机优化，通过一组随机解初始化，通过迭代搜寻最优解。PSO模拟社会，每个可能产生的解表述成群里的一个微粒，每个粒子有属于自己的最佳速度和最佳位置，以及一个由目标函数决定的适应度。所有粒子在搜索空间中以一定速度飞行或在规定的速度范围变速飞行，以最快的速度追随当前空间内搜寻到的最优值来确定全局最优值[1]。具体算法的流程如图1所示。

速度更新公式为：

vi（t）=w*vi-1（t-1）+c1*r1（xpbest（t-1）-xi（t-1））+c2*r2（xgbest（t-1）-xi（t-1））

位置更新公式为：

xi（t）=xi（t-1）+vi（t）

公式中各算子的含义：

（1）w：惯性权重（为大于零的数，w越接近0，收敛优化越快，取值范围一般为[0.4，0.8]）。

（2）c1，c2：个体学习因子、群体学习因子（取值范围[0，4]，一般取值为2）。

（3）r1，r2：两个随机函数，取值范围[0，1]，以增加更新速度的随机性。

（4）pbest：个体经历的最佳位置。

（5）gbest：全局最佳位置。

2 多目标粒子群算法

多目标的粒子群算法主要分为以下六类：复合加权粒子群算法、字典排序粒子群算法、带有子种群的粒子群算法、基于Pareto方法的粒子群算法、混杂的粒子群算法、其他创新型粒子群算法[2]。

目前的多目标粒子群算法大多采用Pareto最优集的方法对多目标解进行寻优运算，采用Pareto方法的多目标粒子群算法的运算框架已经成为一种固定的程序流程和理论方法。因为在多目标进化算法中已有成熟的处理相似问题的办法，所以对这些方法进行有针对性的取舍可解决大部分多目标粒子群优化的问题。

MOPSO算法的步骤：

（1）和单目标粒子群算法相同，初始化种群以及参数设置;

（2）将粒子带入目标函数，求得各粒子的函数值;

（3）初始化各粒子位置以及速度，并用Pareto方法将解以集合的方式储存;

（4）从集合中选取最优值，并用核心更新公式将速度和位置进行更新;

（5）迭代出新的粒子参数再次带入目标函数计算出新粒子的函数值;

（6）从集合中更新最优值;

（7）更新外部储存的集合;

（8）若没有达到优解的条件返回步骤（4）继续运算，直到输出符合条件的优解。

当算法运用到多目标的优化上，必然会遇到下面两个问题。

（1）个体最优解（pbest）的选择问题。

对于单目标优化来说选择pbest，只需要对比一下就可以选择出哪个较优。但是对于多目标来说，两个粒子的对比，并不能对比出哪个好一些。如果粒子的每个目标都要好的话，则该粒子更优。若有些更好，有些更差的话，就无法严格地说哪个好些，哪个差些。

（2）全局最优解（gbest）的选择问题。

对于单目标在种群中只有一个最优的个体。而对于多目标来说，最优的个体有很多个。对粒子群算法来说，每个粒子只能选择一个作为最优的个体（领导者）。

为解决以上两个问题，多目标粒子群算法（MOPSO）对于第一个问题的做法是在空间中随机选择相对优秀粒子中的一个作为历史最优，因为多目标的前提下，无法通过严格的筛选机制选择出真正的全局最优粒子[3]。对于第二个问题，MOPSO则在最优集里面根据粒子的疏密度选择出全局最优。尽量选择空间中粒子较为稀少的位置作为“精英粒子”带领其他粒子寻最优解。

在设计多目标算法时，处理大部分的影响因素都可借鉴其他成熟的多目标智能算法的解决方法。例如选取个体最优时，可用集合的优解代替个体的优解，或者随机选择，将中心放在全局优解的选取上。所以处理全局最好位置的选取是MOPSO的重要影响因素，这一步骤也是MOPSO的重要设计环节。

对于全局最好位置的选取，研究者们提出了很多有效可行的方法。而最常用到的方法是通过选取领导粒子（也被称为领袖粒子），将这样的粒子当作全局的最优解，领导其他粒子达到真正的全局最优解。而每代的全局最优粒子（领导粒子）的选择主要分3个途径。

一是通过以集合的方式选取。判断所含粒子解较好的集合作为选取领导粒子的集，然后用网格法随机选取粒子作为全局的最优解。这种选取方式收敛快，容易使算法陷入局部最优的境地。

二是引入两个粒子群的方法选取。第一个粒子群用于计算粒子的更新速度，调整粒子群飞向全局最优解，用另一个粒子群计算目标优解，筛选出粒子群要跟随的优秀粒子。这种方法能选取更好的全局最优解，但需要大量的数据作为铺垫，不适用于数据量较少的优化问题。

三是引入共享概念。可以共享少部分粒子，使他们先成为全局最好的粒子，也可以优中选优，经过二次筛选，选取全局最优;或者将适应度共享，根据适应度的值为每个粒子寻找最优解。这种寻找全局最优的方式比较灵活，不过需要对算法的运算结构进行改进，并且需要注意提高在收敛后期对全局的搜素速度。

3 改进与展望

針对不同领域的优化问题，研究人员提出了很多具有针对性的改进方案，提高了MOPSO各方面的性能。预计将来，初代粒子的均衡性、算子的运算机逻辑、最优粒子的选择机制、粒子间信息共享的方式是多目标的粒子群算法优化的主要方向。引进新的算法进化机制，提高算法处理复杂问题的能力和算法的运行效率也是改进MOPSO的有效途径。

虽然MOPSO运用在调度方面已经有有效且成熟的方法策略，但在其他问题如路线选择的优化和多个智能算法组合优化的问题上还有欠缺。由于粒子群算法中各粒子的速度和位置是跟随迭代次数不断更新的，是连续的变量，在求取静态优化问题时需要对算法的结构和参数进行更改才能应用。目前对于此方面提出的有效策略还需要继续深入研究，创新改进方法。

[参考文献]

[1]杨明轩.粒子群算法的改进及应用研究[D].长沙：湖南理工学院，2020.

[2]郑友莲，樊俊青.多目标粒子群优化算法研究[J].湖北大学学报（自然科学版），2008（4）：351-355.

[3]冯茜，李擎，全威，等.多目标粒子群优化算法研究综述[J].工程科学学报，2020（3）：10.

（编辑 何 琳）

Influencing factors and improvement strategies of multi-objective particle swarm optimization algorithm

Lu Xinxin1， Wang Huaidong2

（1. Basic teaching and Research Department of Jilin University of business and technology， Changchun 130507， China; 2. School of electrical and electronic engineering， Changchun University of technology， Changchun 130012， China）

Abstract：Particle swarm optimization algorithm is used to solve optimization problems in all walks of life because of its unique operation structure and excellent convergence speed. Nowadays， the speed of intelligent production mode is accelerating， and the single objective particle swarm optimization algorithm can not meet the needs of various industries for algorithm optimization. The multi-objective optimization of particle swarm optimization algorithm is born. Through the improvement of the algorithm， the particle swarm optimization algorithm is realized to solve the multi-objective optimization problem， but while solving the multi-objective optimization， the factors affecting the particle swarm optimization algorithm are also increasing. This paper focuses on the influencing factors and improvement strategies of multi-objective particle swarm optimization algorithm.

Key words：particle swarm optimization; multi objective; improvement strategy

作者简介：鲁欣欣（1989— ），女，吉林四平人，助教，硕士研究生;研究方向：智能算法，大数据。