建筑物立面重复模式的点云投影直方图分割方法

胡鹏飞，周拥军

(上海交通大学 船舶海洋与建筑工程学院，上海 200240)

智慧城市、数字地球等概念的提出和应用，使既有建筑物的高精度三维重建成为研究人员关注的重点问题[1]。三维激光扫描技术(LiDAR)通过发射激光并收集从目标反射信息，得到大量三维点云，LiDAR技术因采集速度快、精度高、信息损失少，成为了既有建筑数据采集的主要手段[2]。建筑中存在大量的门、窗、梁、柱等重复模式，这些结构具有共同的几何形状和物理参数，随着BIM技术的广泛应用，对这些重复模式进行精确重建对BIM建模和分析具有重要意义。本文选择某建筑物的立面，将窗户作为重复模式，研究原始点云提取建筑立面后重复模式的提取和高精度重建方法，旨在提高目标提取的速度和精度，为快速构建既有建筑的BIM模型提供理论和方法。

目前，提取建筑物点云轮廓的思路主要有两种：一种是通过将点云数据根据深度或者强度等信息转换成二维图像，然后运用图像识别的方法来进行轮廓线的提取。赵泉华[3]等人将点云数据转化成深度图像，构建一种以非规则图形为标识随机模型，对任意形状的点云外形进行提取。程效军[4]将三维点云进行切片，分成不同层的平面点云，将每一层点云转换成图像，运用图像处理中的形态学算子提取轮廓，并反求得到点云边缘特征点。另一种思路则是直接对点云进行轮廓提取，目前使用较为广泛的方法有凸包算法[5-7]、三角网法[8-10]、AlphaShape算法[11-15]等。此外，一些学者还提出了一些新方法：樊晶晶[16]通过万向切片得到包含轮廓点的点云数据，定义基于法向量夹角的模式向量，在与模式向量欧氏距离最小的组内提取轮廓。童礼华[17]提出一种改进的轮廓密度估计方法，通过自动计算格网密度阈值，精确提取建筑物轮廓。

虽然目前对于建筑物点云轮廓的研究很多，但是还有不足之处。基于深度图像的算法虽然利用了成熟的图像处理技术，但同时也存在以下问题[18]：首先，三维点云转换成二维图像的过程必然会丢失一部分空间信息，造成提取精度的降低；其次，由于转换过程中需要人工对格网进行划分，不同的划分方式会导致图像的分辨率发生变化，影响分割效果；最后，如何将三维点云和二维图像进行配准也是一个难题。AlphaShape算法和凸包算法比较适用于点云密度比较均匀的情况，对于密度不均匀的情况和某些点云缺失部位容易造成轮廓的误提取[19]。三角网法得到的结果比较稳定，但是得到的轮廓线边缘会存在一些狭长的三角形部分，不能准确反映出目标的现实轮廓，从而无法精确提取边缘点[20]。针对上述问题，并考虑到大多数建筑物由大量的重复几何构件组成的特点，提出了一种基于投影点云特征直方图的算法，由于直接使用了目标的几何特性，该算法简单、无需进行点云变换、抗噪能力强，且不存在轮廓过度提取现象。

1 基于投影点云特征直方图的点云语义分割

建筑物主体分为建筑物立面部分和建筑物的内部结构，均存在大量的重复结构，对于建筑物的外立面来说，其主要的重复结构为窗户，而对于建筑物内部来说，主要重复结构为墙、门、梁、柱等。

本文针对具有规则形状的大量建筑物重复模式的语义分割问题，提出了一种基于投影点云特征直方图(Projective Point Feature Histogram, PPFH)的提取方法。该方法考虑了重复结构和墙体的点云分布特点，利用二者在不同方向上的点云密度差异，通过统计直方图的方法确定重复结构的近似边缘线，最后完成边缘的规则化和误差分析。

本文仅以建筑物立面中的重复模式—窗户为例介绍本文的算法，建筑物立面及窗户的算法流程主要由以下步骤组成：

1)将建筑物点云投影至xoy平面，使用PCA方法分析，确定建筑物主方向。同时将坐标轴按照PCA分析结果进行旋转，完成姿态调整；

2)根据建筑物立面特点，寻找点云密度最大区域，提取建筑物立面；

3)投影至建筑物立面并绘制立面各方向点云分布直方图；

4)通过窗体与墙面点云分布差异确定窗户精细边缘线位置；

5)通过合适的阈值确定边缘线点；

6)利用混合LS-TLS方法进行边缘重建和误差分析。

具体流程图如图1所示。

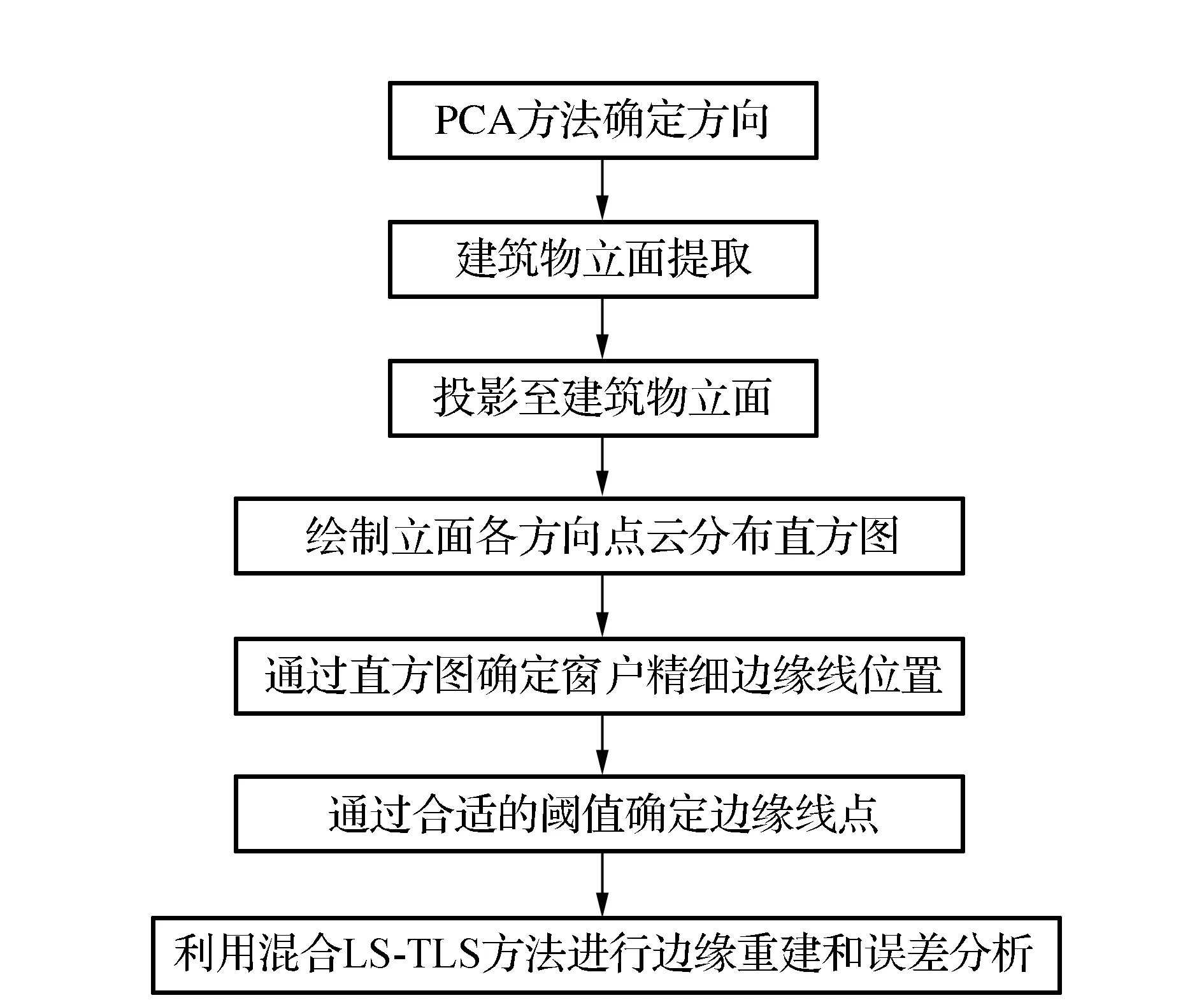
图1 窗户精细重建流程图

1.1 PCA分析确定主方向

由于LiDAR三维扫描时设置的测站坐标系与建筑物立面主方向不一致，因此首先需要确定建筑立面的主方向，即找到建筑物立面与测站平面之间的夹角，采用主成分分析(principal component analysis，PCA)确定其主方向。PCA方法是一种将多个变量降为几个主要成分并保留原始数据大部分主要信息的统计分析方法，在数据降维、机器学习等方面有重要作用[21]。

本文扫描场景为上海交通大学闵行校区行政B楼某面墙体，该墙体上共有50个大小形状都相同的窗户，扫描仪器型号为LEICA P40，其距离扫描精度为1.2 mm+10 ppm，扫描间隔为0.02 m，利用cyclone软件对该建筑物目标区域进行预处理，粗提取了建筑物的墙面，预处理后原始点云数据的三维视图如图2所示。

图2 原始点云数据三维视图

设该建筑物点云数据总个数为m，所有数据表示为{xiyizi}(i=1,2,…，m)，由于三维点云的z轴方向垂直于水平面，与测站坐标系z轴方向一致。因此只需将点云投影至xoy平面，投影点的主方向即可表示建筑物立面的方位，为此，只考虑所有点云的平面坐标，将坐标中心化：

(1)

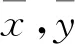
(2)

根据PCA方法原理，散度矩阵S的最大特征值所对应的特征向量即为该建筑物在xoy平面内的主方向。因此，将散度矩阵进行奇异值分解得到特征向量和特征值，其中最大特征值对应的特征向量方向即为建筑物主方向，并计算主方向与原坐标轴之间的夹角θ，并将坐标轴绕z轴旋转θ，完成建筑坐标变换。转换前后该建筑物的投影图如图3所示，可以看出，经过PCA分析后，点云数据的x，y轴与建筑物的主体方向一致，证明用PCA分析方法寻找建筑物主方向是可行的。

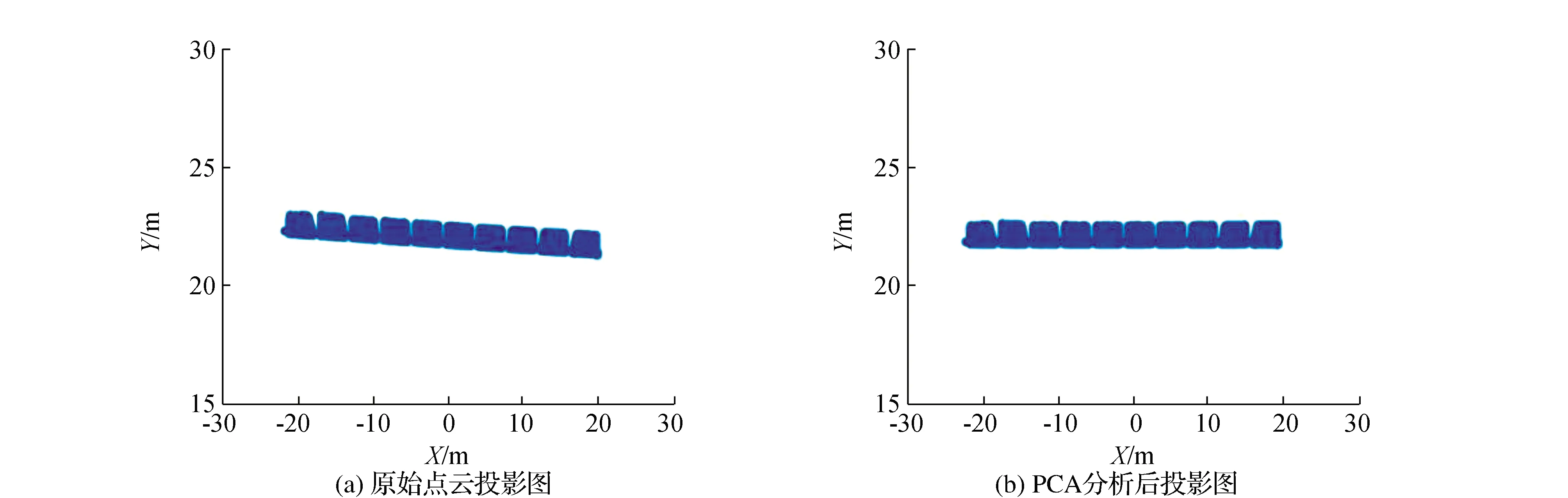
图3 PCA分析前后投影图

1.2 建筑物立面提取

为得到窗户轮廓，首先精确获得建筑物立面的位置。从建筑物的原始三维视图可以看出，该建筑物由于事先进行过预处理得到了粗略的建筑物立面，该点云除了建筑物立面外，还包括少量噪声点以及非立面部分(如窗户装饰区域)，由于建筑物立面部分点云密度远大于其余部分点云密度，为此，可以根据不同部分的点云分布情况精确提取建筑物立面位置。经过PCA分析后的建筑物点云数据投影至xoy平面，如图3(b)所示，沿着y轴方向划分为大小相等的若干区间，并统计每个区间内点的数量，绘制点云分布直方图。直方图的宽度选择对于精确提取立面有很大的影响，若选择较大宽度的直方图，得到的峰值区间宽度远大于实际立面宽度，会导致检测结果不准确。但是如果使用较小宽度的直方图，那么属于某一区间的边缘点可能会落在相邻的区间内，使每一个区间的观测值变少，局部极大值在点云分布直方图中不明显。因此合理选择直方图宽度对提取结果有很大的影响。根据相关规范，一般的框架结构和砖混结构墙体厚度分别为180 mm和240 mm，因此本文取两者平均值200 mm作为直方图宽度对该建筑物进行区间划分，并绘制出统计直方图，如图4所示。

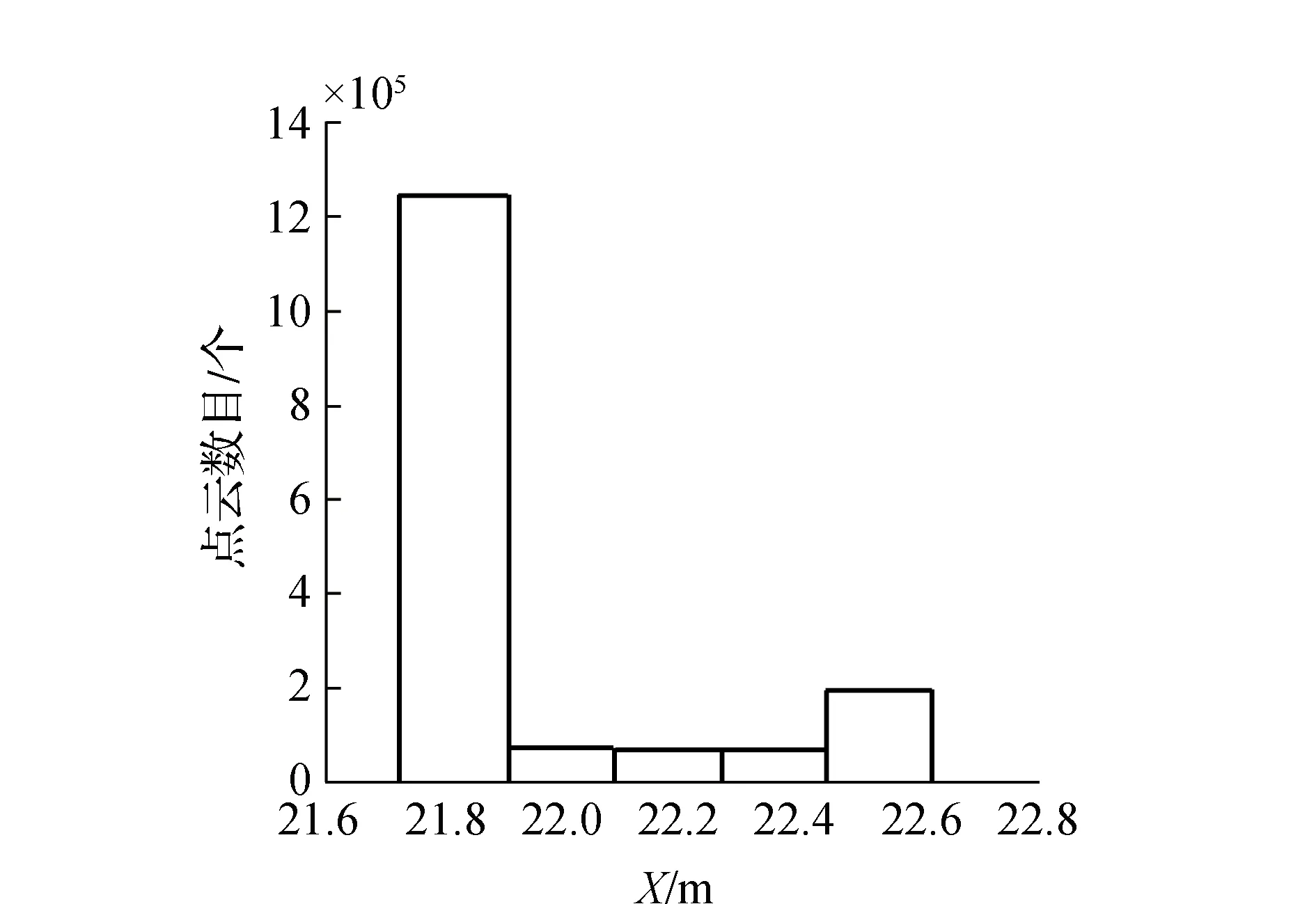
图4 点云分布直方图(y方向)

从点云分布直方图可以看出该建筑物点云在y方向上共有两个峰值区间，二者之间的距离约为0.6 m，且点云数量远大于第二个峰值对应的点云数量，因此根据点云结构可以判断，第一个峰值区间对应建筑物的立面，第二个峰值区间对应窗户装饰部分，由于本文仅考虑重建窗户轮廓，不考虑窗户其余装饰区域，因此仅取第一个峰值区间作为建筑物立面点云。

1.3 投影直方图确定窗户边缘线

测量过程中，受窗户打开或关闭状态、窗户和窗帘材质、测量误差、目标遮蔽等因素的影响，导致窗户部分的点云数据的空间分布不具备明显的规律，且大部分的激光会透过窗户，反射回扫描仪的点云很少，因此，相较于建筑物立面点云来说，窗户部分的点云密度很小。而窗户边缘线作为窗户与建筑物立面的交界，在点云分布直方图上必然会出现显著变化。为此，先将墙体平面投影至建筑物正立面(见图5)，并对其第一主方向(x轴)和高度方向(z轴)分别划分若干等间距的区间，分别统计每个区间的点云数目，得到如图6所示的点云分布直方图。

图5 建筑物正立面投影图

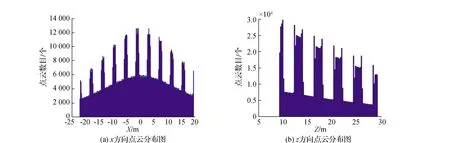
图6 x，z方向点云分布图

结合实际情况和投影图中可知，该建筑物立面存在5个×10个重复结构的窗户，水平边缘线共20条，竖直边缘线10条。这与两个方向点云分布直方图所展现的结果相一致，因此，直方图中极值点左右两侧对应窗户的边缘线。

1.4 窗户边缘点云提取

边缘线坐标可以计算得每个窗户边缘四个角点的粗略坐标，坐标附近一定区域的选择即可获得窗户边缘的点云数据。获取点云数据时，扫描间隔为0.02 m，对于任意一条边缘线，将边缘线横纵方向各偏移0.02 m，得到一个矩形区间，任意落在该区间内的点，即可视为该边缘线上的点。为了比较不同阈值对后续重建精度的影响，随机选择某窗户进行对比试验，图7为阈值0.02 m和0.04 m的边缘点云图，将左边缘线标记为1号直线，逆时针分别为2、3、4号，对于阈值0.02 m的情况，四条边点数目分别为92、61、92、173，对于阈值0.04 m的情况，四条边点数目分别为210、183、206、298，根据后续的精细化重建结果得出两种取值方法对于精细重建的结果影响不大，但是小的阈值选取可能会造成某些边缘线上的点数据过少，而若继续扩大阈值，则对重建结果会产生较大影响。因此，对于规则形状的重复窗户边缘线提取，阈值宜取两倍的扫描间隔。

图7 不同阈值的边缘点图

1.5 轮廓提取效果对比

为了验证本文提出的PPFH算法轮廓提取效果，将本文方法与基于深度图像的方法和基于AlphaShape算法对比。对于深度图像方法，将三维点云整个区域投影至xoz平面，划分为500像素×500像素大小的网格，采用(Inverse Distance Weighted，IDW)内插方法确定每个网格的特征灰度值，将其转换为二维灰度图像，随后使用Canny算子进行边缘检测，提取对应的边缘点云。对于Alpha-Shape算法，取α=2.5 cm对该三维点云数据进行轮廓提取。图8展示了本文算法(PPFH)、基于深度图像的方法和Alpha-Shape算法所提取结果(本文算法仅提取窗户边缘)。

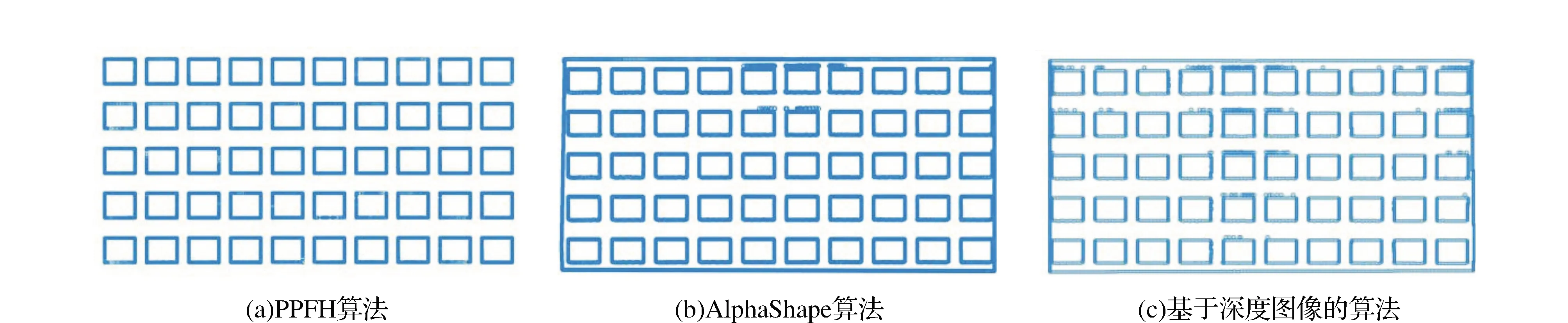
图8 窗户提取结果

通过对比3种算法可以获得50个窗的基本轮廓，但是基于深度图像的方法和AlphaShape算法过度提取窗户边缘线，AlphaShape算法通过设置alpha半径提取轮廓线，在窗户边缘部分遮挡的情况下会将缺失区域确定为边界，从而影响提取效果，而基于深度图像的提取算法需要将点云转换为图像，除容易在点云缺失区域存在边缘误提取之外，相互转换既增加数据处理的复杂度也降低提取精度。而本文提出的PPFH方法直接利用建筑物的常见几何特性，无需对原始点云进行压缩和变换，算法原理简单，轮廓提取准确，对存在边界遮蔽的情况下也能准确提取，具有较好的实用性。

2 边缘规则化与误差分析

成功提取边缘点后，为实现边缘轮廓的高精度重建，本文采用文献[22]中提出基于EIV模型的混合LS-TLS方法来解决二维直角建筑物的边界重建问题。该方法采用了海森法和正交距离法代替了传统的斜截式表示直线方程，综合考虑建筑物的几何关系以及测量误差，构造建筑物含误差模型，并使用混合LS-TLS的解算方法。

窗户模型共由4条相互正交的边缘构成，假设θ表示左侧边缘线的法向对应的坐标方位角，ρi，i=1,2,3,4分别表示坐标原点到窗户四条边缘线的距离。由于相邻窗户边缘线之间相互垂直，则窗户的函数模型表达式为：

(3)

式中：xij，yij分别表示第i(i=1,2,3,4)条边缘线上第j个点的坐标，βx=cosθ，βy=sinθ。利用混合LS-TLS方法可以解出窗户边缘线的距离参数ρ=(ρ1，ρ2，ρ3，ρ4)T和角度参数β=(βx，βx)T，窗户的长宽：

l=|ρ1-ρ3|，

d=|ρ2-ρ4|.

(4)

获得窗户的几何参数后，利用近似的精度估计方法计算得到角度参数和边缘线距离参数的理论协因数阵，根据误差传播原理[23]可以得出每个窗户几何参数所对应的理论协因数阵应满足：

(5)

根据单个窗户的几何参数和误差分析结果可以判断出这50个窗户属于同一类窗户，随后将计算所得的50个窗户的几何参数进行统计分析，取50个窗户的平均值作为此类重复窗户的共同参数，计算对应的长度、宽度的均方根。长、宽均方根为：

(6)

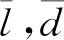
所有边缘线点进行重建和误差分析，结果如表1所示，分析数据可知：PPFH方法得到的窗户平均几何参数为：长3.029 3 m，宽2.186 7 m。单个窗户角度平均误差±0.000 3°，最大误差±0.000 9°，长度平均误差±6.6 mm，最大误差±16.4 mm，宽度平均误差±5.7 mm，最大误差±10.6 mm，统计所得长度均方差0.009 4 m，宽度均方差0.008 8 m，所得结果优于AlphaShape算法和基于深度图像的方法。

表1 3种方法窗户的几何参数及误差

根据相关规范，结合统计分析结果可判断建筑物窗洞口尺寸为3 m×2.1 m，根据现场勘查判断，长宽误差主要以下原因造成的：首先，在建筑物装修过程中需要对外墙进行抹灰，通常来说单边间隙为1.5 cm；其次施工过程中和测量过程均会由于各种原因产生一定的误差，本文所得的长宽误差在容许范围之内，因此本文将窗户的平均值作为窗户的共同几何参数的方法，大大提高精度，反映窗户的实际情况。

3 多样重复模式提取研究

在实际场景之中，建筑物的重复结构相对比较复杂。对于多层建筑物，建筑物外立面的重复模式的大小、位置、类型会随着楼层的变化而改变，如建筑物底楼的立面往往存在门等结构。为解决这一问题，可先将建筑物逐层分割，将复杂的三维点云投影或切片变为平面点云后，通过本文的方法提取重复特征。对建筑物原始点云的分层处理不仅可以在保留特征的前提下提高特征提取的准确度，而且能大幅减少计算的工作量。多层建筑楼板附近的点云密度比其余部分大，因此可以根据点云在竖直方向的统计直方图作为分层的依据。

图9展示了某一工厂某外立面的提取过程：图9(a)为该工厂的原始点云三维视图，该工厂主体共三层，共细分为7个建筑物立面。其中最左侧立面每一层的重复模式不同，因此选取该立面为算例，验证本文算法对不同楼层的重复模式的提取效果。根据本文的算法，先确定建筑物的主方向，然后根据给定阈值对其进行竖向切片，并对得到的切片按高程进行统计分析，得到图9(b)所示的直方图，其中各峰值点代表该建筑物各层楼板位置。得到楼板的位置后，将立面点短根据楼板位置分割，并得到每一层的点云直方图，图9(c)、9(d)、9(e)分别为各层的点云直方图。本算例的重复模式主要是门窗，从图中可以看出一、二楼各有4个重复结构，三楼有2个重复结构。最后，对各楼层按本文方法对其进行精确提取，得到该工厂立面的重复模式提取结果如图9(f)所示，其中，红色结构为门，蓝色结构为窗。

图9 工厂立面提取示意图

建筑物内部的重复模式主要是梁、柱、墙、门等，不同的重复模式其法向量有不同的特点，如梁的法向量与水平面垂直。柱、墙的法向量都与水平面平行，但由于柱的长宽比一般较小，所以其法向量与x，y主方向的夹角都比较小，而墙体往往只有一个方向夹角较小。对比不同重复模式的法向量特点，可以初步得到重复模式的基本类型，并实现重复模式的粗分割。最后，通过对粗分割结果的平差计算，可以得到精确的重建结果。

4 结束语

本文针对现代建筑中大规模存在的形状规则的重复结构，通过PCA方法确定主方向，结合目标物的几何特性和点云的统计规律对结构轮廓进行高精度的语义分割，同时利用混合LS-TLS方法实现边界的规则化和误差分析。通过算例分析表明本文的方法在提取形状规则的重复结构目标的准确度和精度都优于现有的AlphaShape算法，可以广泛应用于对规则重复结构的提取。由于本文的方法利用了重复模式的正交和平行等几何特性，因此主要适用于矩形形状的目标提取，之后的研究应该针对其他复杂结构的提取，以提高算法的适用范围。