基于ANSYS的弧齿锥齿轮非稳态本体温度场分析

蔡瑜瑜

(闽南理工学院 光电与机电工程学院,福建 石狮 362700)

弧齿锥齿轮是一种传动部件，其主要的优势在于传动过程中能够实现高速及重载运转，使用范围非常广泛，并且在航空发动机领域承担着非常重要的角色〔1〕。弧齿锥齿轮运转过程中，由于受到摩擦力的影响，齿轮啮合会产生非常大的热载荷，齿面温度会不断升高，如若温度不能得到有效的控制，必将会对齿面造成一定的胶合破坏。另外，齿轮传动环节，其表面的温度场如若不能实现均匀分布，这时齿轮产生一定的附加热应力，在热应力的作用下，齿侧间存在的间隙会不断减小，严重的会导致齿轮啮合出现卡死或者是停止传动情况。想要让齿轮自身的传动性以及稳定性得到有效的提升，必须对其本体的温度场展开深层次的分析及阐述〔2〕。李子繁〔3〕通过对齿面上存在的摩擦系数和摩擦热流量进行深入研究后得到较为准确的分布信息。王忠达〔4〕通过大量的实验研究后提出可使用摩擦学有关的分析方式对锥齿轮展开深入的研究及探索，该研究方法的提出为后续对弧齿锥齿轮展开热分析提供了强有力的理论依据。陈国定〔5〕在研究时以构建3D有限模型来研究齿轮本体温度场。综上所述，针对弧齿锥齿轮展开研究的内容并未涉及齿宽、模数及齿轮高速重载情况等因素带来的影响。

文章通过构建有限元模型，结合ANSYS软件仿真，得到齿轮非稳态本体温度场分布情况，在此基础上，分析齿轮的模数和齿宽等因素对该齿轮温度场产生的影响，可为改善弧齿锥齿轮传动性能提供理论依据。

1 轮齿非稳态本体温度的热平衡方程与边界条件

通过对传热学有关的理论内容进行分析后得知〔6〕，轮齿的非稳态温度场热平衡方程如式(1)所示。

(1)

在上述公式中，k所代表的为齿轮材料自身的热导系数，ρ所代表的为齿轮材料自身的密度，C所代表的为齿轮材料自身的比热，T所代表的为齿轮自身温度。

方程的边界条件，如图1所示。

处在啮合工作状态下的齿面，n区计算公式如式(2)所示。

(2)

处在齿根以及齿顶及非啮合工作状态下的齿面，t区计算公式如式(3)所示。

(3)

以齿轮端面的s区而言，其计算公式如式(4)所示。

(4)

以轮齿自身的下部分界面而言，其d区的计算公式如式(5)所示。

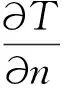
(5)

以分齿截面而言，p区以及q区的计算公式如式(6)所示。

(6)

初始条件：

T=f(x,y,z,t)|t=0=φ(x,y,z)

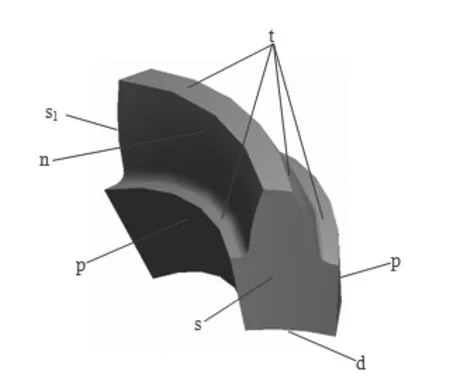
图1 轮齿的计算区域示意图

2 摩擦热流的计算

啮合状态下，齿轮转动过程中齿面呈现出的运动以相对运动为主，运动方式有两种，一种为滚动，另一种为滑动。通过力学得知，齿轮处在滚动状态下产生的摩擦力相对比滑动状态下产生的摩擦力要小。为此，在分析摩擦热时，仅考虑滑动摩擦产生的摩擦热量，其可用Q进行表示，详细情况如式(7)所示。

Q=fPv

(7)

在上述公式中，滑动摩擦系数f，按照以往的经验数据可得知，f正常区间一般为0.045～0.065。P0所表示的为在啮合情况中，齿轮接触点的承受的最大接触应力；v所表示的为啮合环节齿轮自身的滑动速度。

两啮合齿轮吸热不同，引入分配系数ξ，两者各自的摩擦热如下所示。

主从齿轮在瞬时状态下得到的输入热，如式(8)所示。

(8)

通过上述公式计算，即可得出主从齿轮处在啮合状态下得到的热流输入，即q1、q2，如式(9)所示。

(9)

在上述公式中，ω1所表示的为主动轮自身的角速度；ω2所表示的为从动轮自身的角速度；v1所表示的为啮合情况下，主动轮自身的线速度；v2所表示的为啮合情况下，从动轮自身的线速度，b1所表示的为啮合点呈现出的接触半宽。

以赫兹公式可得知：

(10)

(11)

在上述公式中，E1所表示的为主动轮自身的弹性模量；E2所表示的为从动轮自身的弹性模量；μ1所表示的为主动轮自身的泊松比；μ2所表示的为从动轮自身的泊松比。

3 齿轮非稳态本体温度场的计算

以主动轮为例，在开展计算时所选取的各项参数以及指标等均以表1所示。具体的实体模型示意图如图2所示。与主动轮所对应的从动轮选取的齿数为60，其能够实现的传动功率为P=210kw，主动轮转速r=4400r/min，齿轮材料型号选择45号钢，详细情况如下表2所示，环境温度设置为52 ℃。

表1 主动轮各项参数示意表

表2 齿轮材料各项参数示意表

图2 弧齿锥齿轮实体模型

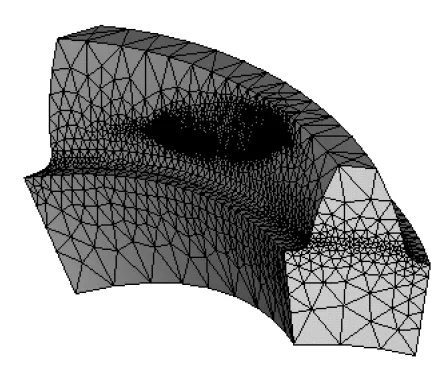
图3 主动轮轮齿有限元模型

3.1 结果分析

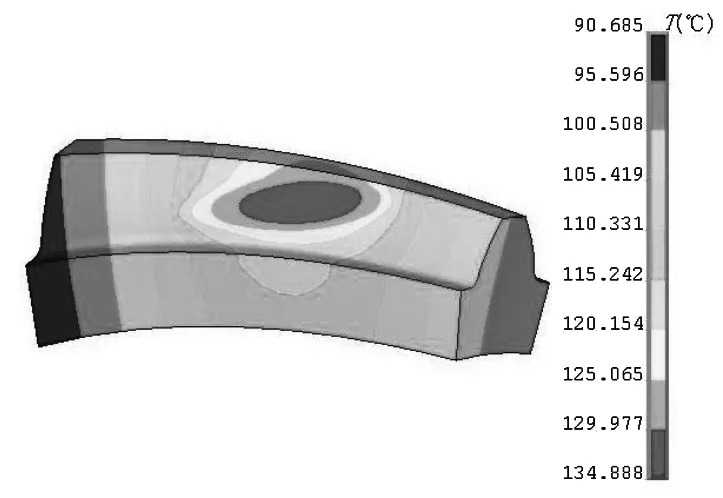
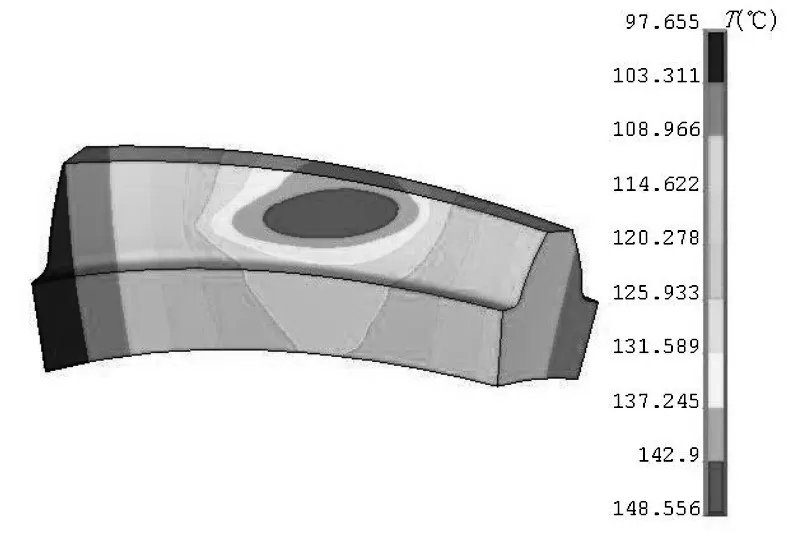
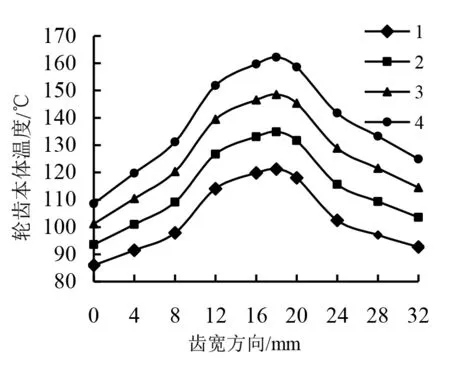
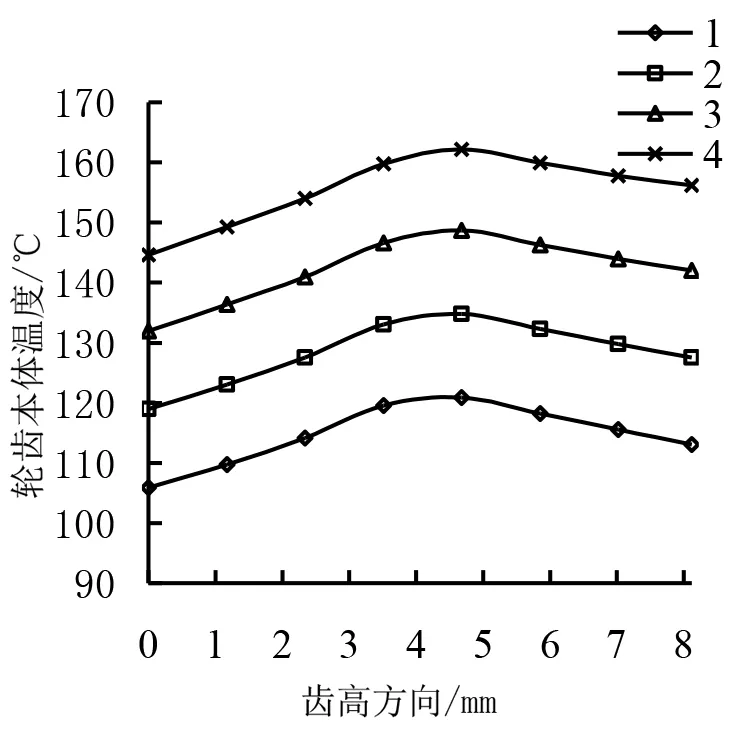
针对齿轮丧失润滑系统后进行弧齿锥齿轮温度场分析，即可得出齿轮非稳态温度场情况。轮齿有限元模型具体如图3所示，结合ANSYS软件进行仿真实验，由此得出弧齿锥齿轮非稳态温度场出现的温度分布，如图4所示。通过对图4分析后得知，在有润滑条件状态下(t=0s)，随着时间的推移，逐渐向无润滑条件下转移(t=60s、120s、180s)的温度场分布情况。图5a、5b分别表示为啮合齿面非稳态本体温度场在分度圆处的(在齿宽方向)变化情况和轮齿中间截面的变化情况(在齿高方向，齿根指向齿顶)，其图中的系列1，2，3，4分别表示齿轮啮合时间为0s、60s、120s、180s。

通过对图4以及图5进行分析后得知：

1)如若环境条件出现变化，齿轮传动在时间推移下逐渐从润滑状态转向无润滑状态，最终会导致润滑系统失去原有的功能。另外，随着时间不断延长，由于齿轮自身失去润滑效果，本体温度会不断上升，热量逐渐增加，当温度达到材料胶合边承受的最大温度后，此时齿轮会丧失工作能力。

2)通过对轮齿温度分析发现，其啮合接触点的中心点是整个轮齿温度的最高区域。齿面温度变化在0s的温度为121.248 ℃，在60s的温度为134.888 ℃，当时间延长至180s，此时温度达到了162.235 ℃。

3)啮合状态下，齿轮自身的温度场呈现出的变化情况有两种，一种为齿面温度随着时间延长，温度逐渐增加；另一种为时间不断增加，齿面高温区会不断延伸，并向齿顶发展。综上所述，由于啮合齿面长时间处在无润滑状态下，其散热能力有所减退，而热追赶现象随着时间的增加逐渐恶化。

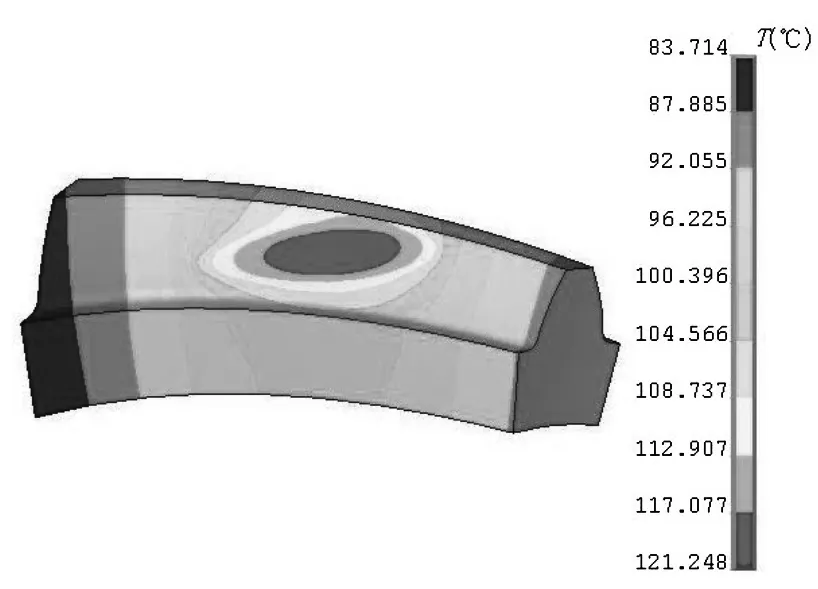
(a) t=0 s

(b) t=60 s

(c) t=120 s

(d) t=180 s

(a)

(b)

3.2 齿宽对轮齿非稳态本体温度场的影响

能够对齿轮本体温度产生影响的因素非常多。文章在研究时主要针对齿宽以及模数等两个因素进行着重分析。图6a和6b分别表示t=0s、t=180s时，齿面本体温度在轮齿中间部分沿齿高方向的变化情况，系列1，2，3分别表示齿宽为18mm、22mm、30mm，通过分析图6可知：

1)在180s内，齿轮齿宽逐渐增加，其最大本体温度处温升会随之增加。当齿宽处在22mm时，最大本体温度处温升比18mm齿宽时最大本体温度处温升增长了357.81%；当齿宽处在30mm时，最大本体温度处温升比18mm齿宽时最大本体温度处温升增长了1 289%。

2)齿轮本体温度会受到来自齿宽变化产生的显著影响。究其根源主要在于，齿宽增加啮合面呈现出的摩擦力逐渐增多，所产生的热流量随之增加，另外，齿轮端面的散热能力削弱，齿轮冷却速度变缓，由此以来，齿轮体积不断增加，其热传导能力就会逐渐缩减。

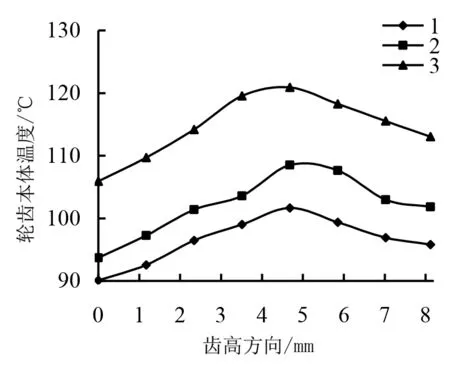
(a)

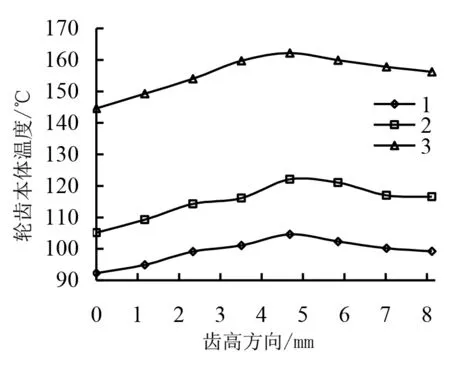
(b)

3.3 模数对轮齿非稳态本体温度场的影响

图7a和7b分别表示t=0s、t=180s时，齿面本体温度在分度圆处沿齿宽方向的变化情况，系列1，2，3分别表示模数为3mm、4mm、5mm，通过分析图7可知：

1)在180s内，齿轮模数不断增加，其最大本体温度温升会随之降低。究其根源主要是，齿轮处在无润滑状态下，模数增加后，齿轮体积随之增加，其热传导能力逐渐下降，而这种现象对于流传热系数产生的影响相对比摩擦热流量小。

2)在180s内，模数处在4mm时的最大本体温度处温升相对比模数处在3mm的最大本体温度处温升降低了50.98%；模数处在5mm时的最大本体温度处温升相对比模数为3mm的最大本体温度处温升降低了64.24%。

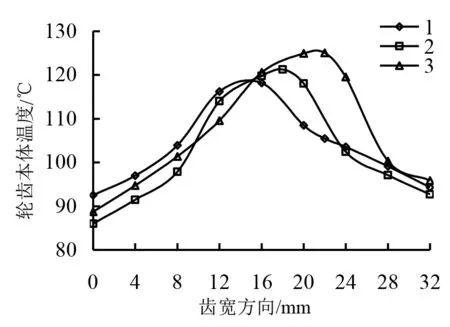
(a)

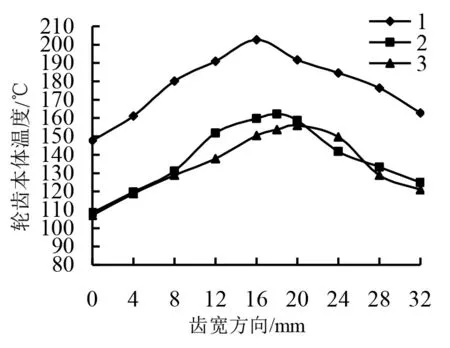
(b)

4 结语

文章针对齿轮非稳态本体温度场展开研究时，通过构建完善的有限元模型，以此分析轮齿非稳态本体温度场整体变化情况，并借助ANSYS软件开展仿真试验，在此基础上，分析齿轮的模数和齿宽等因素对该齿轮温度场产生的影响，结论如下：

1)齿轮非稳态本体温度随时间变化而急剧上升，最高温度区域范围扩大并进一步向齿顶移动。齿轮啮合状态下，接触点中心区域即为轮齿自身温度的最高区域，齿轮端面区域则为温度的最低区域。

2)齿轮齿体区域温度会比齿面区域温度低，而齿体区域的温度会比轮齿端面区域高。以齿宽方向而言，该区域温度变化以抛物线形式展现。

3)轮齿非稳态本体温度会受到齿轮自身齿宽出现变化产生的影响，齿宽增加，则温度上升。而齿轮模数不断增加，轮齿非稳态本体温度温升会随之降低。