集装箱码头岸边作业坠箱事故系统动力学仿真

杜晔 胡甚平 高德毅

摘要：为定量评估集装箱码头岸边作业坠箱事故发生概率，对其构建系统动力学（system dynamics， SD）模型。基于坠箱事故的故障树分析（fault tree analysis， FTA）结果，将事故因素按照“人-机-物-环-管”进行分类，分析因素发生的概率和基本事件相互之间的影响关系。在验证利用SD模型得到的事故发生概率与FTA的定量计算结果具有一致性的基础上，考虑实际情况下各因素的动态特性和相互关系，得到利用SD模型得到的概率结果较FTA的概率结果更接近实际情况。采用SD模型在FTA的最小径集中选择安全策略，并通过模型仿真检验选择的安全策略能否使码头岸边作业坠箱事故发生概率下降到预期水平。给集装箱码头的建议：首先要针对人的因素采取安全措施，其次是机械因素，再次是管理因素。

关键词： 集装箱码头作业; 安全管理; 故障树分析; 系统动力学仿真

中图分类号： U693+.35; U698.6    文献标志码： A

Abstract： To evaluate the probability of container falling accidents in quayside operation at container terminals， the system dynamics （SD） model is constructed. Based on the fault tree analysis （FTA） results of container falling accidents， the accident factors are classified by “human-machine-material-environment-management”， and the probability of the factors and the influence relationship among basic events are analyzed. Based on the verification that the accident probability by the SD model is consistent with the quantitative calculation result of FTA， considering the dynamic characteristics and relations of various factors in the actual situation， the probability result obtained by the SD model is closer to the actual situation than that of FTA. The SD model is used to select the safety strategy within the minimum path sets of FTA， and to verify whether the selected safety strategy can reduce the probability of container falling accidents to an expected level.Suggestions for container terminals： first， take safety measures for human factors， followed by mechanical factors， and again management factors.

Key words： container terminal operation; safety management; fault tree analysis; system dynamics （SD）simulation

0 引 言

集装箱码头发生坠箱事故不仅会造成货主、承运人和码头的损失，而且会给航道及港口水域带来安全隐患[1]。因此，控制坠箱事故发生是集装箱码头作业安全管理的重点之一。近年来随着集装箱码头作业量的增长，码头岸边作业坠箱事故时有发生[2]，因此需要深入研究事故发生机理并提出进一步降低该类事故发生风险的策略。

国内外学者对码头作业安全和船舶坠箱事故进行了积极的研究。梁承姬等[3]就集装箱桥吊操作事故可能发生的原因绘制出故障树，并在定性分析基本事件结构重要性后，提出码头预防桥吊操作事故的建议。DARBRA等[4]研究了港口发生事故及其原因的分类，显示集装箱相关事故已经上升到了首位，碰撞是首要的原因。SUNARYO等[5]探讨了用故障树的方法评价集装箱桥吊作业的风险。潘洋等[6]讨论了人的因素对桥吊操作事故的影响。故障树分析（fault tree analysis， FTA）是一种系统安全分析方法，可通过演绎方法定性和定量地分析各类基本事件对坠箱事故的影响，并可用来为码头选择安全措施和管理策略以减少坠箱事故的发生[7]。

集装箱码头是复杂动态系统，其作业过程中各类事件相互影响、状态不断变化。ALYAMI等[8]针对复杂动态系统的安全研究尝试引入系统动力学（system dynamics， SD）方法進行建模。李海丽等[9]提出应用SD研究和分析系统安全的动态发展。张阳等[10]通过SD仿真分析多因素影响下某类风险的动态变化情况。

SD方法能够在FTA的基础上研究复杂系统动力机制，即在FTA的逻辑关系基础上完善各因素间动态关系和概率分布，以体现部分因素之间的时滞和反馈效应，再通过仿真来评估安全策略。

1 问题描述

1.1 坠箱事故的故障树

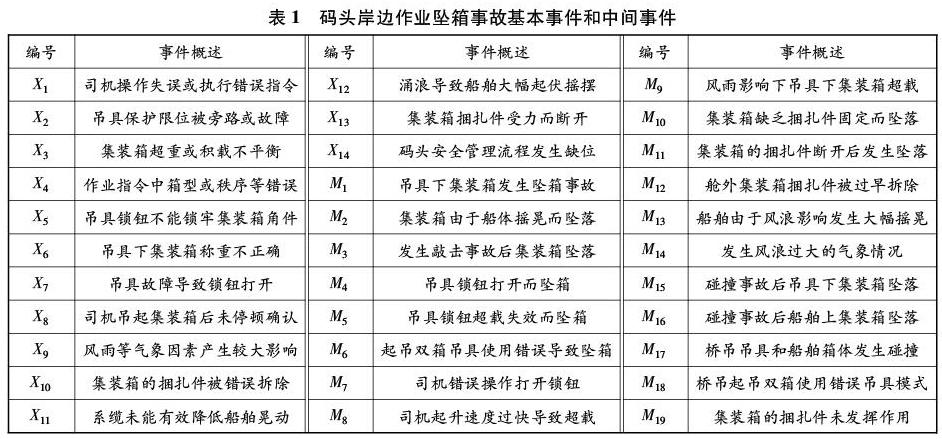
本文结合文献[1-3，6]和近年来集装箱码头发生的岸边作业坠箱事故，将码头岸边作业坠箱事件（T）根据事件发生的逻辑关系分为岸边事故、船舶事故和前两者的共因事故3类，逐步分解得到涵盖了“人-机-物-环-管”的14项坠箱事故基本事件（Xi，i=1，2，…，14）和19项中间事件（Mj，j=1，2，…，19），见表1。基本事件可分类为：人因基本事件X1、X10、X11;机械基本事件X2、X5、X6、X7、X13;物因基本事件X3;环境基本事件X9、X12;管理基本事件X4、X8、X14。

根据逻辑关系将故障树的各项事件绘制成故障树，见图1。M1“吊具下集装箱发生坠箱事故”指吊具起吊集装箱后发生的非船舶原因的3类事故（M4、M5、M6）;M2“集装箱由于船体摇晃而坠落”指集装箱在靠泊的船上由各因素导致的2类事故（M10、M11）;M3“发生敲击事故后集装箱坠落”指集装箱在起吊过程中在吊具和船舶共同影响下发生碰撞而产生的2类事故（M15、M16）。由图1可见，码头岸边作业坠箱事故发生往往是多方面因素共同作用的结果。

1.2 故障树最小割集分析

根据我国现行国家标准《故障树分析程序》（GB/T 7829—1987）和《故障树名词术语和符号》（GB/T 4888—2009），图1的故障树可按照标准进行定性和定量分析。将坠箱事故的故障树通过布尔代数规则整理，可将顶上事件表示为

由式（1）可见，坠箱事故有13项最小割集，按“人-机-物-环-管”对基本事件分类：单因素最小割集仅1项为{X7};双因素最小割集共2项，分别为{X1，X2}和{X2，X4，X8};三因素最小割集共9项;四因素最小割集仅1项。虽然坠箱事故主要由3方面因素引起，但需重点应对少数事件引起坠箱事故的情况。

1.3 FTA的最小径集

FTA的最小径集是顶上事件的充要条件，在最小径集中选择安全策略组合可较经济地达到安全管理效果。通过故障树的式（1）布尔表达式的运算可得到28项最小径集。剔除包含难以控制的环境因素的21项最小径集后余下7项最小径集：{X1，X2，X7，X13，X14};{X1，X3，X4，X7，X10，X13};{X1，X4，X5，X7，X10，X13};{X1，X4，X7，X13，X14};{X1，X7，X8，X13，X14};{X2，X4，X5，X7，X10，X13};{X2，X5，X7，X13，X14}。这些最小径集中基本事件均在5项以上，可见必须采取多方面措施才能有效控制坠箱事故发生概率。

1.4 故障树的灵敏度分析

故障树的基本事件灵敏度有结构重要度和关键重要度。结构重要度表示故障树基本事件发生概率对顶上事件发生概率的影响大小，本文故障树结构重要度排序为X7>X11>X1>X9=X2>X14=X12>X13=X5=X4>X10=X8=X3>X6。关键重要度表示基本事件发生概率的变化率引起顶上事件发生概率的变化率。一般而言，改变发生概率高的基本事件比改变发生概率低的容易，因此在量化分析中关键重要度应用更广，本文在后继的具体场景中进行关键重要度计算。

2 坠箱事故SD建模

码头岸边作业系统的“人-机-物-环-管”中部分因素通常会相互关联且有影响。为此，本文基于FTA，依照码头岸边作业系统建立“结构-功能”的坠箱事故SD模型。该模型通过系统中因素之间的动态关系反映该系统的时滞和反馈效应。本文先进行SD的逻辑建模（确定问题、限定范圍、因素分析、循环反馈关系、形成SD关系图），再进行模型量化（确定变量的初始值和取值方程，变量相互影响关系），然后对该SD模型进行仿真分析。

2.1 坠箱事故SD模型

考虑到SD模型的逻辑建模以FTA为基础，使用FTA对该码头岸边作业系统进行界定，在坠箱事故的故障树逻辑基础上描述各因素在系统中的动态特点和相互关系。此外，SD模型分别从环境因素的时滞特性（发生后有持续时间）、人的因素和管理因素的反馈特性以及机械因素的退化性和可维修特性等方面对逻辑建模进行分析。

从环境因素（X9、X12）看，当有较大风雨影响时产生涌浪的概率较大，即X9的状态影响X12发生概率。同时，在风雨和涌浪等环境下人员易受到影响，码头也会采取应对措施，即人的因素（X1、X10、X11）和管理因素（X4、X8、X14）发生概率会随环境因素的变化而变化。此外，机械故障发生概率会随着作业次数的增加而增加，本文为此增加机械作业次数的水平变量Lwt（维修保养后吊具持续使用的次数），用Lwt与机械因素的反馈结构反映退化性和可维修特性。

根据以上分析，在SD模型的各项状态变量中，X9、X12、X13、X14这些状态变量一旦发生就会持续一段时间（风雨开始后会持续，类似于安全缺失状态产生后需要经过一段时间才能被发现并纠正），因此在SD模型中分别增加表示这些自变量维持时间的水平变量TX9、TX12、TX13、TX14，通过这些水平变量与状态变量的关系反映自变量的持续状态。根据这些关系构建坠箱事故SD模型，见图2。

2.2 SD模型的量化

故障树中基本事件和中间事件是状态变量（基本事件是自变量，中间事件是因变量），坠箱事故是水平变量。根据SD模型，一定作业数量下的坠箱事故数量可反映坠箱事故风险水平的高低。

2.2.1 状态变量中的自变量

SD模型是基于坠箱事故FTA界定的，则SD模型状态变量中自变量的状态分布可视为二项式分布，对应的故障树基本事件发生概率作为该二项式分布的发生概率[11]。根据码头安全管理和安全评价的相关文献[1-3，6]以及作者经验，在汇总分类各项基本事件后，在概率比较的基础上对故障树中基本事件发生概率进行赋值，见表2（表中预计概率指基本事件不受其他因素影响时的发生概率）。构建SD模型时，在故障树中基本事件发生概率基础上，根据实际工作经验对状态变量中自变量的概率分布的动态特点进行描述。

环境因素对人的因素和管理因素会产生不同的影响，恶劣环境会使得由人的因素导致的事件发生概率升高;而管理因素与环境因素和人的因素形成负反馈回路，其发生概率随着环境因素的发生而下降。参考表2，对SD模型中人的因素和管理因素对应的自变量的变化进行赋值，见表3。

对机械因素（X2、X5、X6、X7、X13）进行分析，当考虑机械多状态退化性和可维修性时，SD模型可采用故障率曲线的形式体现该特性。机械因素在作业过程中由于损耗而性能退化，机械发生故障的概率随着Lwt的累积而上升。如图3所示，机械设备在一定阶段内保持稳定的故障率曲线斜率（该阶段内故障率采用平均故障率），在作业数量累计超过了一定值后故障率曲线斜率变大（随着作业次数的增加故障率增长加快）。而码头对机械的维修和保养可使机械故障率恢复到初始的水平（图3中作业数量t0、故障率P1处）。

SD模型中将机械发生故障的故障率曲线作为Lwt的分段线性函数，且在采取检修保养后复位。由于检修保养越频繁需要投入的资源越多，所以码头根据实际情况采取不同的标准。本文SD模型预估吊具作业的4个机械因素（X13非吊具作业）在不同分段内的故障率，见表4。

由表4可知，一旦发生了机械故障，若X14也发生，则机械将在故障状态下继续工作，这些故障再次发生的概率会大幅上升。实际操作中，X5和X6可能是操作人员将该安全保护限位设施旁路造成的，因此假设机械再次发生故障的概率达到0.05;而X2和X7发生则需要Lwt≥10 000。

2.2.2 中间变量的方程设置与状态概率分布

故障树中间事件对应状态变量中的因变量，根据逻辑门的与或关系对相关的因变量进行计算后得到其状态取值。以各要素涉及的作业次数为时间变量（如涉及X9的作业次数为TX9），由于风雨较大会增加涌浪幅度，即X9发生会使得X12发生概率上升，且X12发生影响下一作业时刻X12发生的概率。由此假设X9发生概率分布为：在X9未发生时，其发生概率为二项分布B（1，0.1%）;在X9发生后其持续时间为TX9。假设X12发生概率分布为：在X9发生时，其发生概率为二项分布B（1，60%）;在X9和X12均未发生时，X12发生概率分布为二项分布B（1，0.1%）;在X9未发生、X12发生时，X12发生概率分布为二项分布B（1，30%）。

此外，假设SD模型中自变量维持时间的水平变量均服从正态分布，在自变量发生后其在维持时间内都处于发生状态，超过维持时间后恢复到原发生概率状态。水平变量TX9、TX13、TX14概率分布密度f（TX9）、f（TX13）、f（TX14）根据经验假设如下：

3 SD模型仿真算例

针对具体的码头岸边作业场景，比较SD模型仿真得到的坠箱事故发生概率与FTA的定量计算结果以验证系统结构的一致性，再在此基础上考虑各因素的动态特性和相互关系。

3.1 基于FTA的SD模型仿真

由于坠箱事故是小概率事件，采用模型仿真方法在较短周期内有可能产生较大的偏差，这就需要大量的模拟仿真。为此，在不考虑SD模型自变量相互之间影响和时滞效应，仅采用FTA的基本事件发生概率作为自变量的概率时，对SD模型进行仿真，看仿真规模多人才能够使坠箱事故的水平变量与FTA的顶上事件发生概率具有一致性。

针对以上SD模型描述的作业场景根据表2的赋值对式（1）进行顶上事件发生概率计算可得，FTA得到的坠箱事故发生概率为6.0×10-5。对SD模型设置参数INITIAL TIME=0，TIME STEP=1，FINAL TIME=106进行5次仿真，得到的結果见图4。由图4计算可知，100万次作业中发生坠箱事故的次数在59次左右，即仿真的坠箱事故发生概率平均为5.9×10-5。由此可见，在此仿真水平下，SD模型对坠箱事故的小概率事件仿真与FTA具有一致性。由图4还可见，增加仿真次数可降低坠箱事故概率的波动幅度。

在SD模型中引入自变量的动态特性后，码头作业系统发生坠箱事故的发展机制由于变量之间的复杂关系和反馈回路而难以直观判断，需要通过仿真反映坠箱事故的发生情况。在SD模型考虑各要素的变化特点以及相互之间影响的关系后，采用FINAL TIME=107进行6次仿真，得到结果见图5。仿真结果显示，事故发生总体概率大幅度下降，仅有2.9×10-6。在引入自变量的动态特性和相互关系后，SD模型仿真的坠箱事故发生概率的数量级与实际经验更为相符。

3.2 模型的灵敏度分析

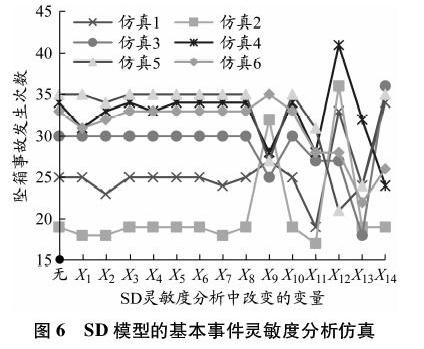
如前文所述，在具体场景下可用FTA方法的灵敏度分析计算基本事件关键重要度。采用表2的赋值计算的关键重要度排序为：X2>X1>X7>X11>X12>X14>X10>X13>X4>X8>X9>X5>X3>X6。通过改变自变量水平进行仿真后比较坠箱事故发生次数来对自变量的灵敏度进行排序。根据此方法，对每个变量分别降低20%的水平，采用FINAL TIME=107进行6次仿真，每次仿真采用不同的随机序列，记录单变量变化后每次仿真得到的坠箱事故总数，见图6。

由图6可见，在不同的随机序列下，某些基本事件的发生概率会产生不同的波动。根据各故障引起事故的变化量进行排序：X13>X11>X12>X1=X2>X7=X9=X14>X4>X10=X8=X5=X3=X6。比较FTA与SD模型的灵敏度分析排序可见，自变量灵敏度位置顺序有了明显不同。这显示，当考虑了自变量相互之间的关系后，基本事件对顶上事件的灵敏度发生了变化。

根据灵敏度分析，可在考虑安全管理策略时优先对灵敏度较高的基本事件采取措施，以更有效地降低坠箱事故发生概率。由于SD模型中自变量之间的关系，针对灵敏度变化较大的自变量还需进一步分析采取管理措施的可行性。例如，X13在作业时由船方负责，因此码头可采取的措施具有局限性。又如，X12的控制比较困难，且在灵敏度分析中发现其概率降低时坠箱事故发生概率上升，通过深入分析可知该情况是X12影响了X4、X9和X14造成的，因此可针对这类基本事件采取相应的措施。

3.3 采取安全措施后的SD模型仿真

从仿真结果可见，SD模型仿真的坠箱事故发生概率水平虽然与实际状况类似，但考虑到作业量饱和的集装箱码头每台桥吊年装卸作业量可达20万自然箱，大型集装箱码头年吞吐量超过100万自然箱，坠箱事故达到六西格玛安全风险水平（3.4×10-6）对于大型码头来说仍然难以接受。假设目标集装箱码头年吞吐量为100万自然箱，如预期坠箱事故发生次数小于1起，则需进一步采取安全管理措施来降低风险，将坠箱事故发生概率控制在1.0×10-6以内。

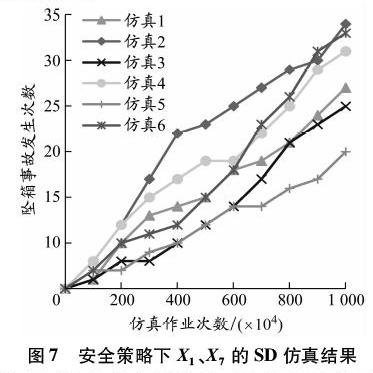
根据最低合理可行原则（as low as reasonably practicable， ALARP），只要将风险水平降低到可接受水平，投入的资源越少越好。为此，码头根据因素的灵敏度分析和最小径集，对码头岸边作业的坠箱事故选择安全管理策略集{X1，X2，X4，X7，X8，X14}，对标当前状况与预计概率之间的差距，对基本事件中的人的因素、机械因素和管理因素采取安全措施以降低坠箱事故的风险水平。首先针对人的因素采取安全措施，如通过对桥吊司机的培训以防止误操作使其发生概率降低，预计下降幅度为50%;其次针对机械因素采取安全措施，如将吊具检修保养的周期从10 000次作业缩短到5 000次作业以内，以降低X7的发生概率（同步降低X2的发生概率）。SD模型采用FINAL TIME=107进行6次仿真，结果见图7。坠箱事件发生概率期望下降至2.3×10-6，虽然下降幅度约达20.7%，但仍未达到预期的坠箱事故发生概率水平。因此，需要针对管理因素进一步采取安全措施。

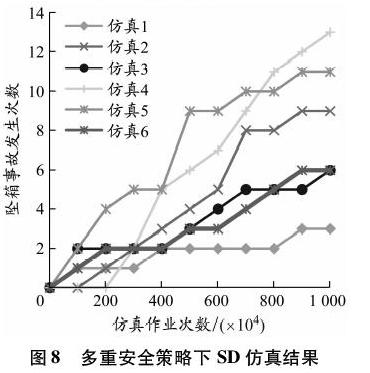
管理因素的基本事件X4、X8和X14可通过桥吊作业指令交叉校验、加强现场作业规范监督提醒和多岗位管理对意外事件的交叉确认等安全措施来降低其发生概率。在假设这些措施使X4、X8和X14发生概率下降50%的情况下，SD模型采用FINALTIME=107再进行6次仿真，得到的结果见图8。结果显示在针对人的因素、机械因素和管理因素所采取的安全措施的共同作用下，发生坠箱事故的平均概率降至0.80×10-6，达到预期的风险控制范围。

4 结 论

从“人-机-物-环-管”的安全要素分类对集装箱码头岸边作业坠箱事故故障树分析（FTA）中的基本事件进行讨论，分析基本事件之间的相互关系和基本事件发生的动态特性，根据FTA的系统设定建立集装箱码头岸边作业坠箱事故SD模型，仿真结果与实际状况更为相符。在此基础上，通过FTA和SD模型的灵敏度分析同时结合FTA的最小径集选择安全策略，并通过SD模型仿真检验安全措施达到预期效果时坠箱事故发生概率是否在预期的风险控制范围内。根据SD模型验证的管理措施，集装箱码头首先要针对人的因素采取安全措施，加强桥吊操作人员的安全意识并在作业中加强提醒，降低操作人员操作失误和不规范操作的概率并及时纠正作业指令的错误;其次要对机械因素采取安全措施，及时对设施设备进行检修保养，发生故障后及时跟进安全措施并维修;再次对管理因素采取安全措施，加强现场安全监控，减少安全管理缺失持续时间。SD模型中的部分状态变量的赋值和安全管理措施落实后的效果的取值是作者根据主观经验判断确定的，在码头实际应用时可以对所采集的相关作业数据进行汇总分析，这将是下一步的工作。

参考文献：

[1] 刘萧.坠箱问题期待重视[J].中国船检， 2017（9）： 52-55.

[2] 陈良玉， 梁承姬.桥吊坠箱事故树分析[J].上海海事大学学报， 2006， 27（2）： 25-28.

[3] 梁承姬， 王重华， 潘洋.岸边集装箱起重机大车操作安全分析[J].中国工程机械学报， 2006， 4（3）： 339-343.

[4] DARBRA R-M，CASAL J. Historical analysis of accidents in seaports[J]. Safety Science， 2004， 42（2）： 85-98. DOI： 10.1016/S0925-7535（03）00002-X.

[5] SUNARYO， HAMKA M A. Safety risks assessment on container terminal using hazard identification and risk assessment and fault tree analysis methods[J].Procedia Engineering， 2017， 194： 307-314.DOI： 10.1016/j.proeng.2017.08.150.

[6] 潘洋， 梁承姬， 郑惠强.基于人因的集装箱岸桥安全操作分析[J].中國安全科学学报， 2012， 22（10）： 65-71.DOI： 10.16265/j.cnki.issn1003-3033.2012.10.006.

[7] BAKLOUTI A， NGUYEN N， MHENNI F， et al. Dynamic fault tree generation for safety-critical systems within a systems engineering approach[J]. IEEE Systems Journal， 2019， 14（1）： 1512-1522. DOI： 10.1109/JSYST.2019.2930184.

[8] ALYAMI H， YANG Zaili， RIAHI R， et al. Advanced uncertainty modelling for container port risk analysis[J]. Accident Analysis & Prevention， 2019， 123： 411-421.DOI： 10.1016/j.aap.2016.08.007.

[9] 李海丽， 陈勇， 张文龙， 等. 矿山顶板事故的FTA-Fuzzy-Vensim分析方法探究[J]. 安全与环境工程， 2019， 26（4）： 147-151， 160. DOI： 10.13578/j.cnki.issn.1671-1556.2019.04.023.

[10] 张阳， 席永涛， 胡甚平， 等. 水上货物运输风险演化系统动力学仿真[J].上海海事大学学报， 2018， 39（1）： 19-24.DOI： 10.13340/j.jsmu.2018.01.004.

[11] HAUPTMANNS U. The impact of differences in reliability data on the results of probabilistic safety analyses[J]. Journal of Loss Prevention in the Process Industries， 2011， 24（3）： 274-280. DOI： 10.1016/j.jlp.2010.09.008.

（编辑 贾裙平）