基于变权灰云模型的深远海域海上风电场选址

赵阳 王凤武 张云鹏

摘要：为实现深远海域海上风电场能源经济效益最大化，同时保障风电场周边海域的船舶通航安全，提出一种基于变权灰云模型的深远海域海上风电场选址方法。建立深远海域海上风电场选址评价指标体系，采用G1法求取指标常权权重，引入变权理论修正常权权重从而确定变权权重。利用正态云模型替代传统的白化权函数，构建变权灰云模型，对场址进行定性定量评价，依据评分值确定最优场址。实例计算分析表明，最优场址在能源经济效益和船舶通航安全方面均处于优势水平，变权灰云模型在深远海域海上风电场选址中具有良好的适用性和有效性。

关键词： 海上风电场; 变权理论; 灰云模型; 灰云聚类

中图分类号： U698; P751; TM614    文献标志码： A

Abstract： In order to maximize the economic benefit of offshore wind farms in far-reaching sea areas and ensure the navigation safety of ships in wind farms’ sea areas， a method based on the variable-weight gray cloud model is proposed for the offshore wind farm site selection in far-reaching sea areas. The evaluation index system of the offshore wind farm site selection in far-reaching sea areas is established， the constant weights of indices are calculated by G1 method， and the variable weight theory is introduced to modify the constant weights to determine the variable weights. The normal cloud model is adopted to substitute the traditional whitening weight function， the variable-weight gray cloud model is constructed to evaluate the sites qualitatively and quantitatively， and the optimal site is determined according to the score value. The example calculation analysis shows that the optimal site is advantageous in terms of energy economic benefit and ship navigation safety， and the variable-weight gray cloud model has good applicability and effectiveness in the offshore wind farm site selection in far-reaching sea areas.

Key words： offshore wind farm; variable weight theory; gray cloud model; gray cloud clustering

0 引 言

海上風力发电已成为清洁能源发展的新趋势。从风能资源角度分析，海上风电能达到陆地风电能量效益的120%～140%，而且海上风电还具有零排放、占地少、运行稳定等诸多优点。近年来，随着新技术的发展以及岸基配套电网设备的完善，海上电力输送、运行维护成本正不断降低，许多国家和地区都将发展海上风电的目光逐渐由近海投向了深远海域。与近海风电相比，深远海域风电开发具有较多优势，如风能资源更为丰富、地域更为宽广、装机容量更大、对海洋环境和船舶通航的影响更小等，深远海域风电发展前景更为广阔。

海上风电场选址作为海上风电场建设的前期工程，涉及海洋资源开发、海洋自然生态保护、船舶航行安全、风电场运行维护等诸多因素，如何协调各种因素，实现能源经济效益最大化以及保障风电场水域船舶通航安全是选址工程的关键。目前，国内外对海上风电场选址的研究主要集中在以下几个方面：一是探测海域风能资源，发掘风能分布规律，确定最佳风电潜力海域;二是结合海上风电场建设水域交通特点，分析风电项目对周边船舶通航的影响，进行交通风险评估或基于船舶避碰要求的安全航线规划;三是对规划风电场海域的地理位置、地形地貌以及社会经济、技术能力、环境资源、运行维护成本等因素进行综合分析，结合风能资源优选场址。研究方法多运用德尔菲法[1]、卫星遥感及地理信息系统（geographic information system，GIS）技术[2-3]、风险框架分析[4]、灰色关联分析[5]、人工势场法[6]、多目标规划[7]、贝叶斯网络[8]、模糊多准则决策[9]等。通过梳理发现，大多数的研究主要围绕近海风电场的选址建设展开，兼顾能源经济效益和船舶通航安全的综合研究较少。在行业发展的新形势下，一方面要积极推进风电场选址的研究向深远海域发展，另一方面应该在选址时注重“效益”和“安全”问题。为此，本文在文献研究和专家调查的基础上，以“效益”和“安全”问题为侧重点，提出一种基于变权灰云模型的深远海域海上风电场选址方法：引入变权理论，修正评价指标常权权重，使指标权重更能符合指标特征客观变化规律，以免较好指标的积极作用掩盖较差或很差指标的消极作用;利用正态云模型替代灰色白化权函数，构建灰云白化权模型对备选场址方案进行定性和定量评价，确定最佳场址。

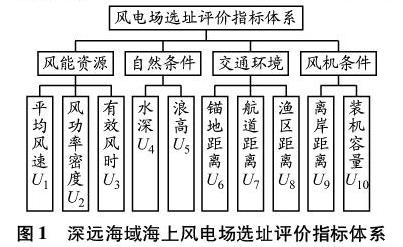
1 深远海域海上风电场选址评价指标体系的建立  结合深远海域特点，对风电场选址主要影响因素进行识别。基于前人研究成果，以能源经济效益和船舶通航安全为侧重点选取评价指标，从风能资源、自然条件、交通环境、风机条件等4个方面入手建立评价指标体系，共10个二级指标，见图1。

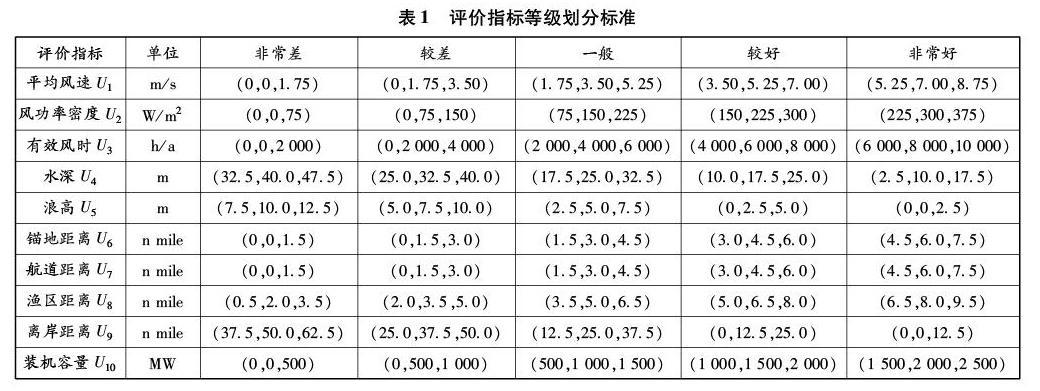
依据深远海域海上风电场场址在能源经济效益和船舶通航安全方面体现的效果，将场址方案划分为非常差、较差、一般、较好、非常好5个等级。依据相关文献和研究，基于三角隶属度函数给出评价指标等级划分标准[10]，见表1。以指标渔区距离为例，该评价指标各等级三角隶属度函数见图2。

2 变权灰云模型

2.1 变权理论求取权重

在系统评价中，指标常权权重能够反映指标对系统的相对重要程度，但没有体现评价对象各指标的数据规律。若采用常权赋权计算，则当多数指标为较好、单一指标为较差或很差时，较好指标的积极作用往往会掩盖较差或很差指标的消极作用，造成评价结果出现偏差，难以体现海上风电场场址实际优劣水平。为更好地体现指标变化在系统决策中的影响，本文用G1法确定常权权重，同时引入变权理论，依据指标数据特征，利用状态变权向量修正常权权重，从而确定变权权重。

2.1.1 G1法确定常权权重

与层次分析法相比，G1法计算量少、操作性强、不需要构造判断矩阵，且无须进行一致性检验[11]。采用G1法确定常权权重的步骤如下：

3 算例分析

以中国某深远海域海上风电场选址为例，进行模型计算分析。

3.1 某风电场选址方案

中国沿海某市为减少海上风电建设对沿岸功能区域的影响，拟在深远海域进行风电场选址，选址方案为5个区域，见图5。

各方案中的数据均由实际测量或观测获得。1、2、3、4、5号方案中计划装机容量分别为250、250、350、500、2 300 MW。通过查阅气象历史观测统计数据，获得平均风速、风功率密度和有效风时;查阅海图和航路指南等，获取水深、浪高以及各方案场址到航道、锚地和渔区的距离，并以各方案场址中心点为基准进行测量，获得各方案离岸距離。各方案评价指标具体数据见表3。

3.2 求取变权权重

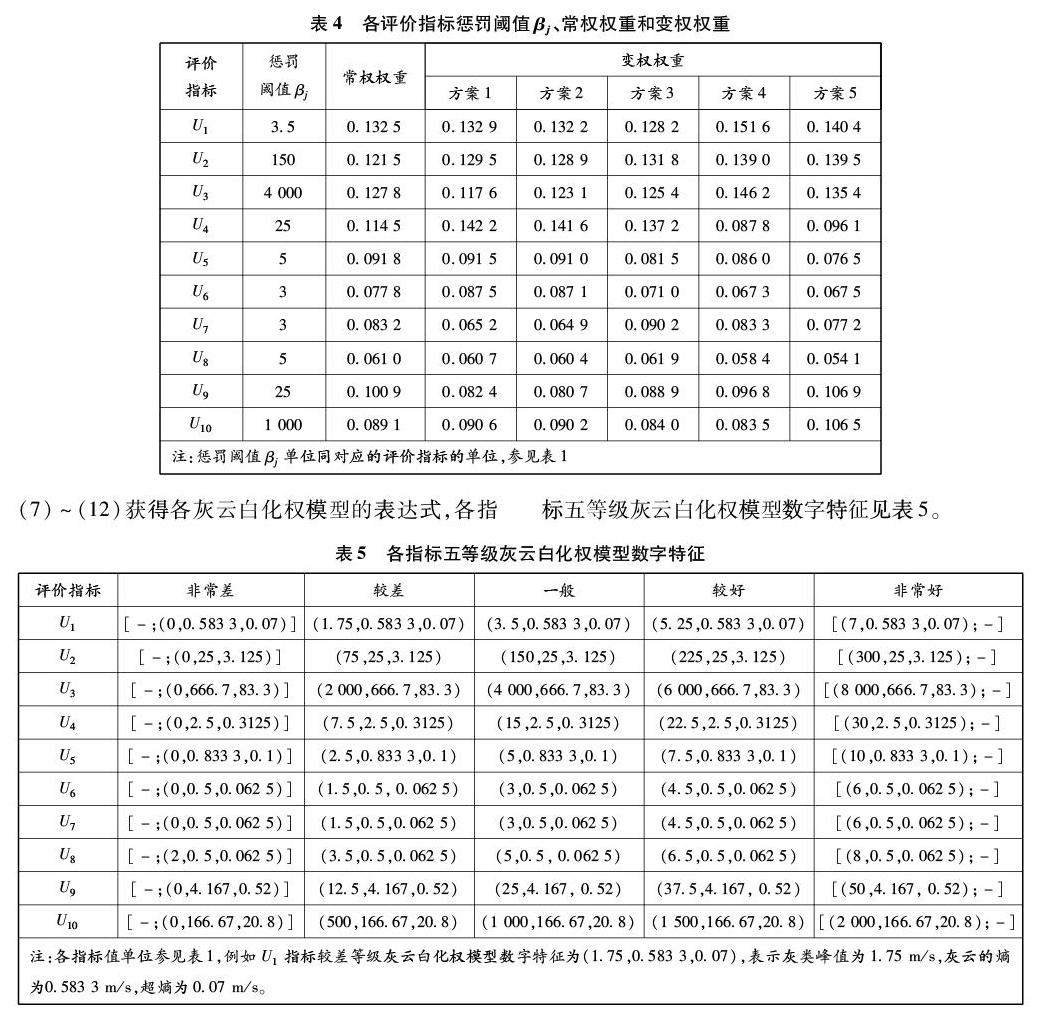
依据评价指标等级划分标准，结合专家建议，确定5个方案的惩罚水平α（本文取α=1）和惩罚阈值βj。依据式（1）～（6）计算得到评价指标常权权重和各方案的变权权重，见表4。

以方案1为例：首先，利用G1法依据式（1）～（4）求得10个评价指标的常权权重;然后，将方案1中各指标数据代入式（5），求得方案1状态变权向量为（1.330 7，1.414 3，1.221 4，1.648 7，1.323 1， 1.491 8，1.040 8，1.320 2，1.083 3，1.349 9）;最后，将方案1常权权重和状态变权向量代入式（6），计算求得方案1各评价指标的变权权重为（0.132 9，0.129 5，0.117 6，0.142 2，0.091 5，0.087 5，0.065 2，0.060 7，0.082 4，0.090 6）。

3.3 建立变权灰云模型

3.3.1 指标数据预处理

3.4 灰云聚类及评价结果

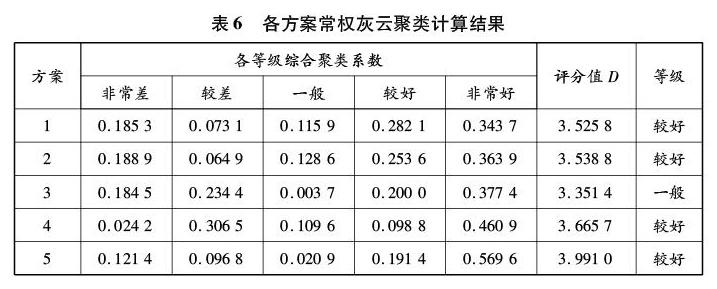
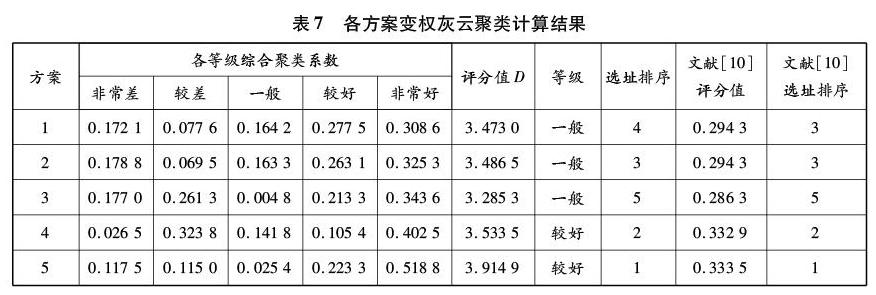
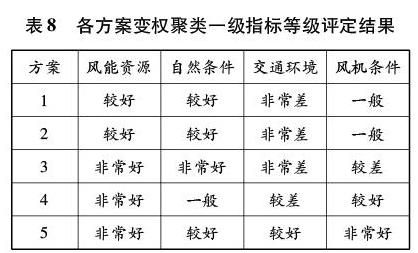
用MATLAB软件进行编程，输入评价指标具体数据，计算各评价指标的灰云聚类系数，结合变权权重得到综合聚类系数，最终计算各方案评分值，确定评价等级。各方案常权灰云聚类计算结果见表6，各方案变权灰云聚类计算结果见表7，各方案变权聚类一级指标等级评定结果见表8。

以方案1中指标U1为例说明变权灰云聚类计算过程。将指标数据输入灰云白化权模型中，并依据式（13）得到100次计算结果的平均值，得到指标U1关于5个等级的灰云聚类系数（0，0，0，0.446 2，0.206 5），利用式（14）得到归一化后的灰云聚类系数（0，0，0，0.683 6，0.316 4）。按照上述步骤可依次求得另外9个评价指标关于各等级的灰云聚类系数，然后利用式（15）可求得方案1的综合聚类系数。最后依据各等级赋值及式（17）计算方案1的评分值为3.473 0，确定方案1的等级为一般。

对比表6和表7中常权赋权和变权赋权的计算结果可知，变权后各方案评分值明显低于常权赋权得到的评分值。这是由于变权赋权方法有效地调动了较差或很差指标的参与度，并在一定程度上保持了较好指标的优势，从而避免了较差指标的消极作用被较好指标掩盖，能更充分体现指标的特征，结果更为客观可信。

由表7评分值得到风电场选址排序为：方案5方案4方案2方案1方案3。分析表8如下：横向来看，方案5在风能资源、自然条件、交通环境、风机条件4个方面均处于较好或非常好的水平;纵向来看，方案5在单一方面均占有优势，使能源经济效益和船舶通航安全都处于较好的水平。与文献[10]的评价结果一致，方案5为终选最优方案，但文献[10]中方案1与方案2的评分值一样，而本文评价得到方案2稍优于方案1，这符合方案2中有效风时更长的优势情况，较为符合实际，这说明变权灰云聚类方法有着较好的分辨力。

通过模型实例分析，对变权灰云模型的优势[21]进行总结：一是引入变权理论修正主观权重，凸显了较差或很差指标对海上风电场选址评价结果的影响，能较全面地体现客观数据在决策中的影响;二是正态灰云模型能够描述评估对象评价等级信息的随机性、灰色性和模糊性，因而评估结果更能体现风电场选址方案的实际情况;三是评估过程中考虑到白化权值的随机性，进行多次计算仿真求取灰云白化权平均值，并把平均值作为各指标等级的灰云聚类系数，因而评估过程更加可靠;四是采用灰云模型进行计算，计算过程更为简便，从定性和定量两方面呈现评估结果，确定风电场选址最优方案，考虑更为全面。

4 结 论

本文充分考虑深远海域海上风电场选址过程中的不确定性和多扰动性等特点，从实现能源经济效益最大化和保障船舶通航安全角度出发，构建风电场选址评价指标体系;引入变权理论，修正评价指标常权权重，消除了主观影响，避免单一较差或很差指标的消极影响被多数较好指标所掩盖，引起决策者的关注;同时采用正态云模型代替灰色白化权函数，构建灰云白化权模型，提升模型的适应空间，从定量和定性两个角度对备选场址方案数据进行分析计算，确定最优场址。通过模型计算和评估结果分析，最优场址无论是在“效益”还是“安全”方面都处于较好及以上水平，实现了“效益”和“安全”的双赢，同时变权灰云模型能够充分考虑系统信息的随机性和模糊性，具有一定的普遍适用性和可靠性，为海上风电场选址提供了新的方法，可在相关领域进行进一步深入研究。参考文献：

[1] HO L W， LIE T T， LEONG P T， et al. Developing offshore wind farm siting criteria by using an international Delphi method[J]. Energy Policy， 2018， 113： 53-67. DOI： 10.1016/j.enpol.2017.10.049.

[2] KUMAR S V V A， PARDE A N， JAGDISH， et al. Offshore wind farm site suitability and assessment along Tamil Nadu coast using RISAT-1 SAR and synergetic scatterometer data[J]. Indian Society of Geomatics， 2019， 13（1）： 138-148.

[3] SALEOUS N， ISSA S， AL MAZROUEI J. GIS-based wind farm site selection model offshore Abu Dhabi Emirate， UAE[C]//The International Archives of the Photogrammetry， Remote Sensing and Spatial Information Sciences. Prague， Czech Republic， 2016， XLI-B8： 437-441. DOI： 10.5194/isprs-archives-XLI-B8-437-2016.

[4] DAI Lijuan， EHLERS S， RAUSAND M， et al. Risk of collision between service vessels and offshore wind turbines[J]. Reliability Engineering & System Safety， 2013， 109： 18-31.DOI： 10.1016/j.ress.2012.07.008.

[5] 陈肖龙. 考虑通航安全因素的海上风电场场址优选研究[D]. 大连： 大连海事大学， 2017.

[6] 薛双飞， 谢磊， 王树武， 等. 海上风电场区船舶A*避碰寻路算法[J]. 中国航海， 2018， 41（2）： 21-25.

[7] JONES D F， WALL G. An extended goal programming model for site selection in the offshore wind farm sector[J]. Annals of Operations Research， 2016， 245： 121-135. DOI： 10.1007/s10 479-015-1828-2.

[8] PINARBA瘙 塁 I K， GALPARSORO I， DEPELLEGRIN D， et al. A modelling approach for offshore wind farm feasibility with respect to ecosystem-based marine spatial planning[J]. Science of the Total Environment， 2019， 667： 306-317. DOI： 10.1016/j.scitotenv.2019.02.268.

[9] FETANAT A， KHORASANINEJAD E. A novel hybrid MCDM approach for offshore wind farm site selection： a case study of Iran[J]. Ocean & Coastal Management， 2015， 109： 17-28. DOI： 10.1016/j.ocecoaman.2015.02.005.

[10] 唐征歧， 江建平， 李子林， 等. 深遠海域海上风电场定量选址方法研究[J]. 交通信息与安全， 2018， 36（2）： 106-111. DOI： 10.3963/j.issn.1674-4861.2018.02.015.

[11] 何锭， 倪富健， 杨顺新. 高速公路事件管理中主要部门影响权重研究[J]. 交通信息与安全， 2011， 29（3）： 89-93， 98. DOI： 10.3963/j.ISSN1674-4861.2011.03.021.

[12] 刘高磊， 戴冉， 王滔， 等. 变权云物元模型在船舶定线制后评估中的应用[J]. 上海海事大学学报， 2019， 40（4）： 66-71， 88. DOI： 10.13340/j.jsmu.2019.04.012.

[13] 李泓泽， 郭森， 唐辉， 等. 基于改进变权物元可拓模型的电能质量综合评价[J]. 电网技术， 2013， 37（3）： 653-659.

[14] 王雁凌， 张雪佼， 阎敬民. 基于变权灰云模型的风电场并网技术性综合评价[J]. 电网技术， 2013， 37（12）： 3546-3551.

[15] 葛兴， 姜波. 基于指标定权灰色聚类的公路平交口安全评价[J]. 交通信息与安全， 2014， 32（6）： 159-165. DOI： 10.3963/j.issn1674-4861.2014.06.000.

[16] 谷倩倩， 丁松滨. 基于综合集成赋权法的航空公司飞行安全风险灰色评估[J]. 交通信息与安全， 2017， 35（6）： 38-45. DOI： 10.3963/j.issn.1674-4861.2017.06.006.

[17] 李晗， 章文俊， 李国帅， 等. 基于灰云和改进AHP的港口船舶应急疏散模型[J]. 上海海事大学学报， 2017， 38（3）： 25-30， 60. DOI： 10.13340/j.jsmu.2017.03.005.

[18] 刘晓佳， 张荀， 汪强， 等. 基于灰云聚类的港口水域通航环境危险度评价[J]. 中国航海， 2019， 42（3）： 55-61.

[19] 朱小飞， 王永君， 李大军. 模糊评价中最大隶属度原则有效性检验[J]. 测绘与空间地理信息， 2016， 39（5）： 135-137， 143.

[20] 强凤娇. 灰色聚类决策归类原则探析[J]. 统计与决策， 2017（18）： 5-9. DOI： 10.13546/j.cnki.tjyjc.2017.18.001.

[21] 王双川， 贾希胜， 胡起伟， 等. 基于正态灰云模型的装备维修保障系统效能评估[J]. 系统工程与电子技术， 2019， 41（7）： 1576-1582.

（编辑 贾裙平）