第七代超深水海洋平台钻机双井架的等强度多目标优化

蒋发光 张 敏 杨秀菊 梁 政

1.西南石油大学机电工程学院 2.石油天然气装备教育部重点实验室 3.中国石油集团宝鸡石油机械有限责任公司

0 引言

随着油气勘探领域的持续加深，超深水将成为未来油气开采的主战场[1-2]。采用主辅双架的第七代超深水海洋平台钻机较第六代海洋平台钻机[3-5]作业能力更强，适应作业水深3 660 m、钻井深度15 240 m，但其环境条件更加恶劣，破坏形式更复杂，导致双井架在作业过程中出现安全系数小、变形大和结构材料使用率低和过度满足要求而结构笨重等设计不合理问题，因此有必要展开双井架优化研究。

国内外对第七代超深水海洋平台钻机双井架的优化研究并不完善，相关的多数研究为陆地井架、浅海域井架、单井架或者非第七代井架。Zhu等[6]在锚杆极限抗拔下对井架锚桩桩身位置进行了优化设计；Guan等[7]对海上模块钻机的井架提出了两种结构加固方案；Lee等[8]在考虑结构性能下对所提出井架结构优化方法的适用性进行了评估；Xu等[9]以重量最轻为目标，对双井架在6种不同工况下进行了优化设计。

等强度是双井架上下各段在满足使用要求下实现同等寿命，最大效率的提高材料利用率。笔者以第七代超深水海洋平台钻机双井架为研究对象，完成72个典型组合工况下的初步设计双井架的有限元力学分析，寻求了双井架在最危险组合工况下不同杆件截面参数时的应力、位移变化规律；结合单因素与响应曲面法[10]，以杆件截面参数为设计变量，以质量最轻，最大应力、最大位移最小为目标，建立目标和设计变量之间的优化函数式，并结合等强度理念（不同高度段应力差异最小）获得了双井架最优结构参数设计。

1 建模

结合初步设计的第七代超深水海洋平台钻机双井架的外形尺寸与截面类型，建立1∶1的双井架有限元模型（图1）。双井架的杆件分为上支柱、中支柱、下支柱和内支撑。杆件采用标准H型钢[11-13]，材料选Q345[12]，其密度7 850 kg/m3、弹性模量206 GPa、泊松比0.28、屈服强度345 MPa，截面参数如表1所示。

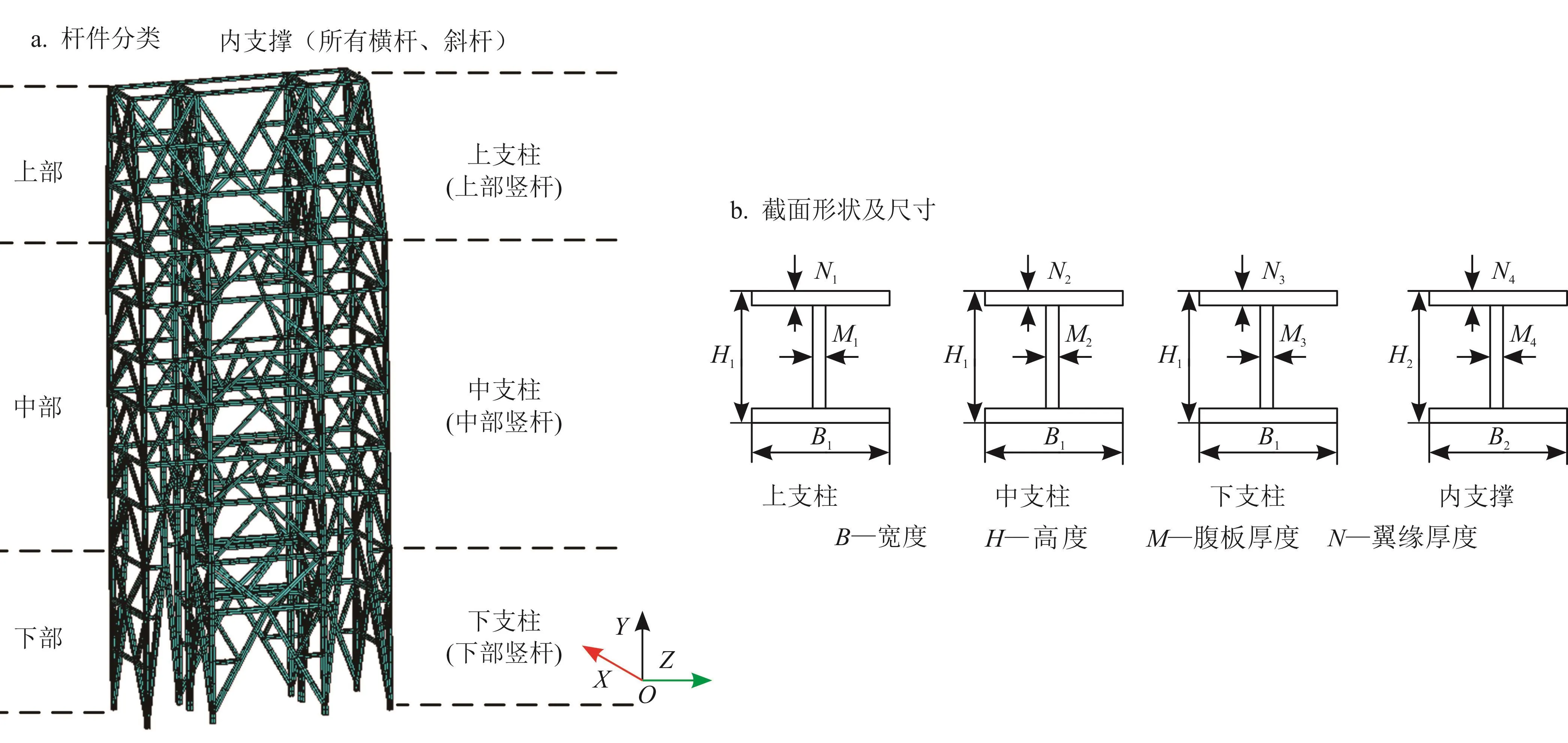
图1 双井架模型及杆件截面图

表1 杆件截面参数表 单位：mm

2 载荷与工况

海洋平台存在的典型工况[14]有：拖航工况、隔水管连接工况、正常作业工况、生存工况和风暴自存工况，分别记为工况A～E。

双井架上安装的主要设备包括天车、顶驱游动系统、大钩、游车和二层台等，合计质量145.4 t，分析模型中通过定义质量单元来等效设置。

2.1 载荷计算

2.1.1 钩载

各工况下双井架的主井架和辅井架所承受的极限钩载不同，如表2所示。

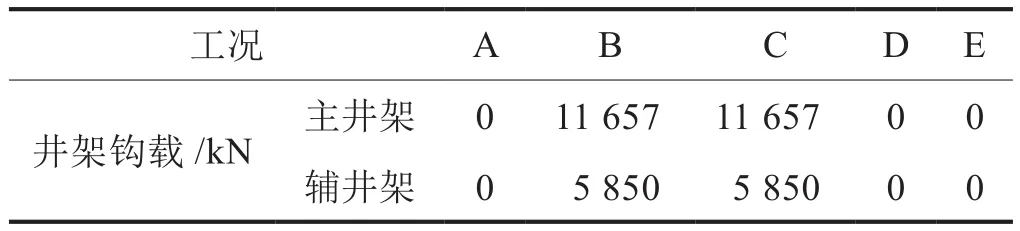
表2 不同工况下的井架钩载计算值

2.1.2 风载

参照API Spec 2C-2004标准[15]，考虑静载、平台运动引起的动载和风载，将动态载荷进行极值化处理，得到等效静力风载公式：

式中Fw表示作用在双井架上的风载，N；P表示作用在井架上的风压（计算结果见表3），Pa；A表示承风面积，即垂直于风向的双井架外轮廓面积[16]，m2；Cs表示部件形状系数，取2[15]；U表示风速，由南海某海洋平台实际统计[14]，m/s。

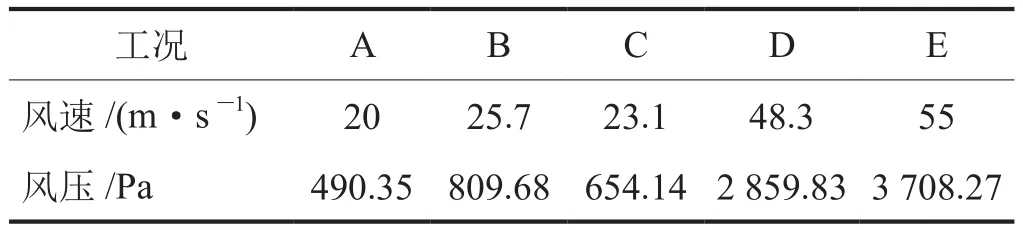
表3 不同工况下计算的在井架上的风压值

由于高度差会导致不同高度段双井架承受的风载不同，将双井架沿高度方向分为6段（图2）。在正常作业工况（风载0°入射）下，由表3和式（1），计算得到各高度段的风载（表4）。

2.1.3 惯性载荷

双井架在各工况下的惯性载荷包括垂直惯性载荷和水平惯性载荷，计算公式如下[15]：

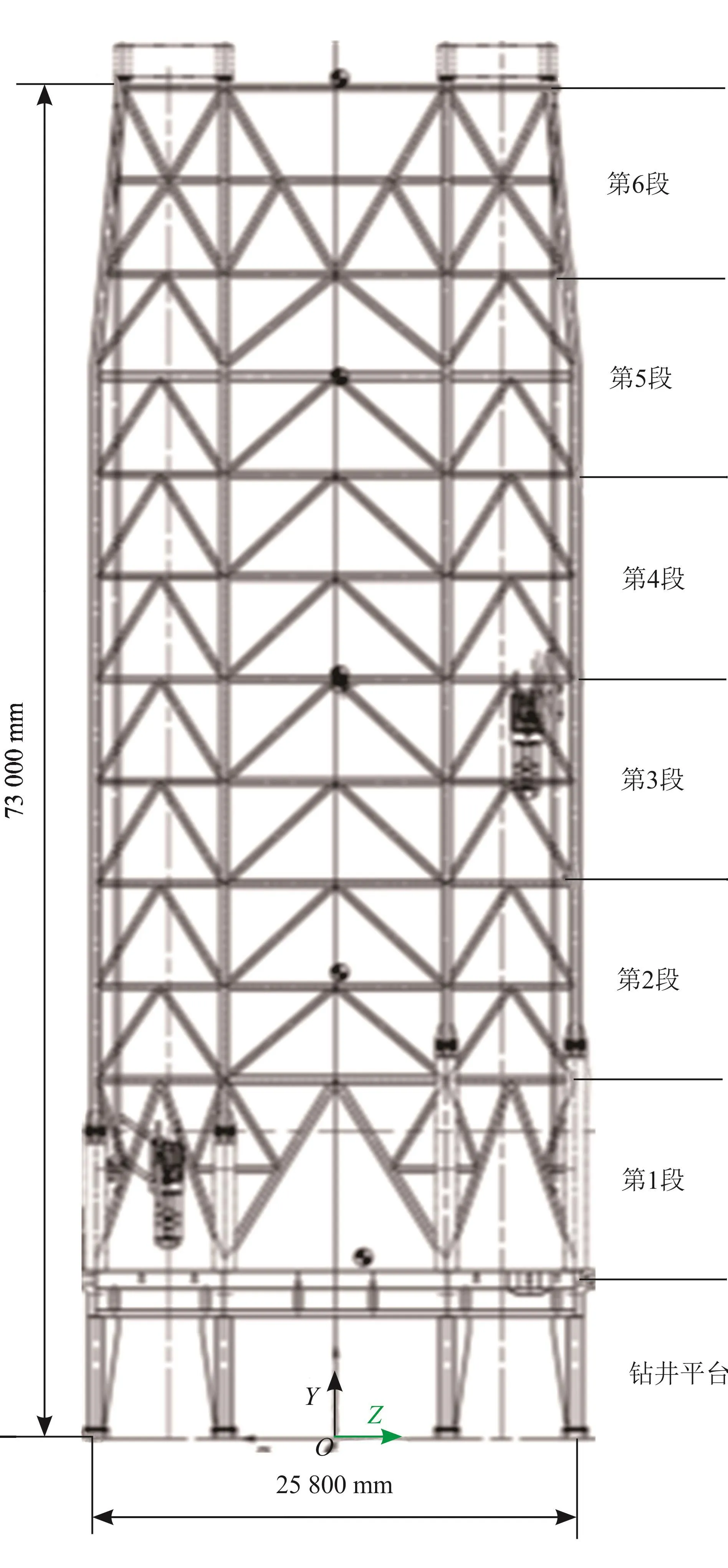
图2 双井架高度分段图

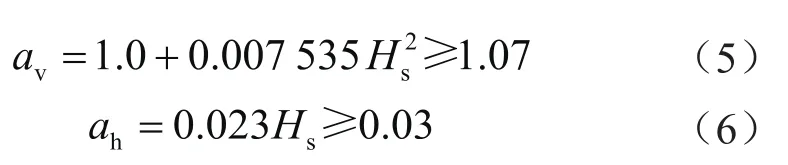
式中Wv和Wh分别表示垂直惯性载荷和水平惯性载荷（计算结果见表5），N；av、ah分别表示垂直、水平方向上的加速度系数；m表示双井架的质量，kg；g表示重力加速度，9.81 m/s2；Hs表示有效波高，由南海某海洋平台实际统计[14]，m。

表4 正常作业工况（风载0°入射）下风载表

表5 惯性载荷表

2.2 典型工况分析

为分析各典型工况，将风载分为0°、45°、90°、135°和180° 5种入射方向，将惯性载荷以加速度方式等效施加。水平惯性加速度分为+X、－X、+Z和－Z等4种方向，垂直惯性加速度分为+Y和－Y两种方向。

以正常作业工况（风载0°入射、+X向水平惯性加速度、+Y向垂直惯性加速度）为例，对双井架定义质量单元，并施加重力加速度、底部全约束、钩载、+X向风载、+X向水平惯性加速度和+Y向垂直惯性加速度，如图3所示。

分析工况A～E在0°风载及8种惯性加速度（4种水平惯性加速度×2种垂直惯性加速度）下的最大应力，结果表明最大应力出现在风暴自存工况。

为寻求双井架的最危险组合工况，将0°、45°、90°、135°和180°5种风向下的风暴自存工况分别设定为组合工况1～5，分析工况1～5在8种惯性加速度下的最大应力，如图4所示，结果表明最危险风暴自存组合工况（风载180°入射、－X向水平惯性加速度、－Y向垂直惯性加速度）的最大应力为234.34 MPa，安全系数n=1.47，小于API Spec 4F-2013规定[17]的1.67。

3 结构参数影响研究

研究双井架在最危险组合工况下不同杆件截面参数时的应力、位移变化规律，为后续的优化提供参数依据。

图 5-a 为截面腹板厚度（M1、M2、M3、M4）、翼缘厚度（N1、N2、N3、N4）对双井架应力的影响。最大应力出现在双井架底脚与平台接触处。随M3、N3增大，底脚与平台的接触面积增大，最大应力递减。随M1、N1、M2、N2、M4、N4增大，底脚处承受支柱和内支撑更大的压力，最大应力递增，增加幅度较小。

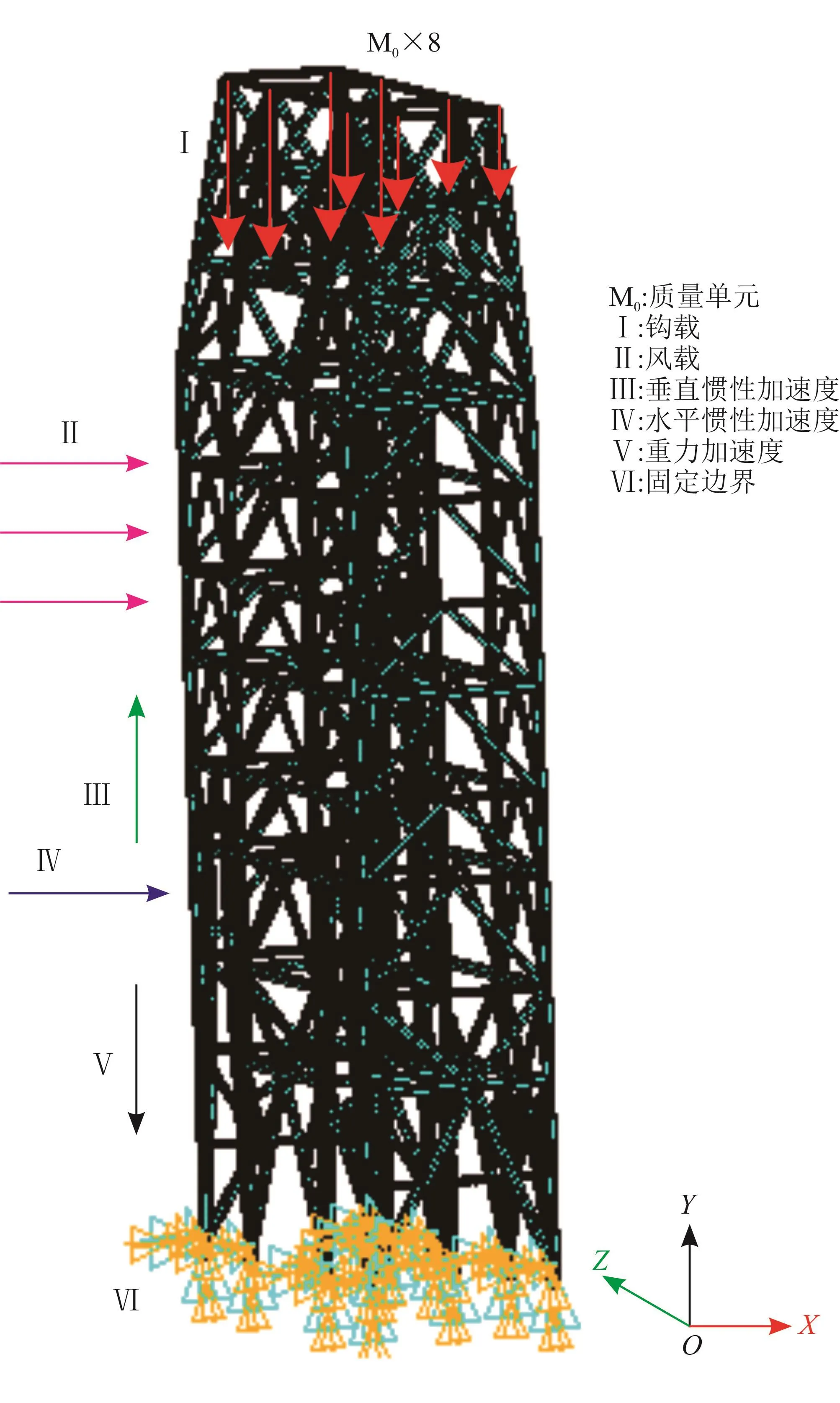
图3 载荷施加与边界条件图

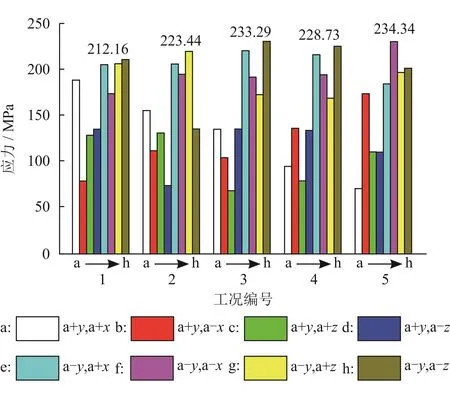
图4 各风向、惯性加速度下的最大应力图

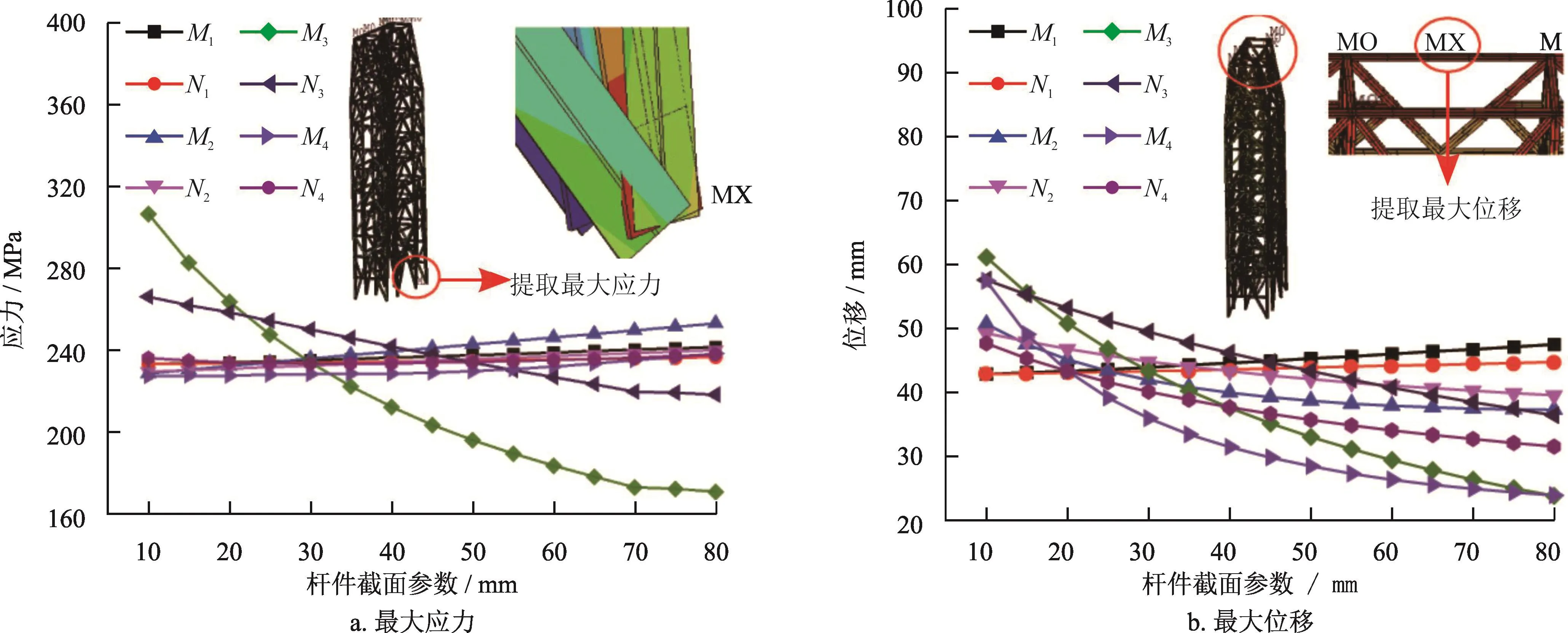
图5 杆件截面腹板、翼缘厚度对双井架的应力、位移影响图

图 5-b为截面腹板厚度（M1、M2、M3、M4）、翼缘厚度（N1、N2、N3、N4）对双井架位移的影响。在初始参数下的最大位移为43.34 mm。最大位移出现在双井架顶部横杆处，主要表现为－X向弯曲变形。随M1、N1增大，倾斜布置的上支柱更笨重，对顶部横杆的压力增大，最大位移递增。随M2、N2、M3、N3增大，各斜杆对顶部横杆的支撑面加大，导致横杆净跨度减小而抗弯刚度增大，最大位移递减。

图6-a为截面宽度（B1、B2）和截面高度（H1、H2）对双井架应力的影响。承风面处的B2对承风面积影响较大，对风载的影响也就较大。最大应力在B2=350 mm出现拐点，是由于变化较大的风载使最大应力位置发生改变。在B2＜350 mm阶段，最大应力出现在中部变截面的横、斜杆处，随B2增大，横、斜杆的风载增大程度与承风面积增大程度一致，而截面积增大，最大应力递减，直至最大应力转变在双井架底脚处；在B2＞350 mm阶段，随B2增大，即使斜杆对下支柱的支撑面积增大，而风载的显著增大使底脚处的最大应力增大。随B1、H1增大，底脚与平台的接触面积增大，但也承受支柱更大的压力，由于两种变化程度的不同，底脚处的最大应力随B1增大而减小，随H1增大整体呈递减（先递减后递增再递减）的趋势。随H2增大，斜杆对下支柱的支撑面积增大，底脚处的最大应力减小。

图6-b为截面宽度（B1、B2）和截面高度（H1、H2）对双井架位移的影响。由于杆件的主要弯曲变形方向（－X向）垂直于腹板截面，腹板截面积对双井架位移的影响较大。最大位移在H2=350 mm出现拐点，是因为变化较大的腹板截面积导致最大位移位置发生改变。在H2＜350 mm阶段，最大位移出现在中部变截面杆件处，随H2增大，变截面杆件的截面积增大，弯曲刚度增大，最大位移减小，直至最大位移转变在双井架顶部横杆处；在H2＞350 mm阶段，随B1、H1、H2增大，各斜杆和上支柱对顶部横杆的支撑面加大，导致横杆净跨度减小而抗弯刚度增大，最大位移递减。随B2增大，支撑顶部横杆的斜杆加重，最大位移递增。

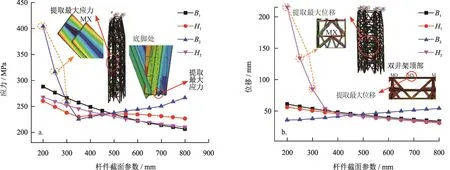
图6 杆件截面宽度、高度对双井架的应力、位移影响图

综述，较大的M3、N3、B1、H1、H2和较小的M1、M2、M4、N1、N2、N4有利于提升双井架的截面强度 ；较大的M2、M3、M4、N2、N3、N4、B1、H1和较小的M1、N1、B2有利于提升双井架的截面刚度。M3、N3对双井架应力影响较大，故在后续的优化中优选M3、N3为设计变量。由于随M3、N3增大，最大应力先减小后在70 mm后趋于水平，故最小值取初始值30 mm，最大值取70 mm。

4 双井架结构参数优化

工况分析中表明，初步设计的双井架在最危险组合工况下的安全系数小于API Spec 4F-2013规定[17]的1.67，最大位移（43.34 mm）大于规范[18]允许值l/400=12 550/400=31.375 mm，下支柱与上段杆件的应力差异较大，降低了材料利用率。针对以上不合理的杆件布局，采用等强度理念对双井架进行截面参数优化，理想结构为：满足强度、刚度要求，质量最轻，最大应力、最大位移最小，不同高度段的应力差异最小。

在优化前，分析杆件截面参数对双井架质量的影响（图7），随各截面参数增大，质量线性递增，M4、N4、B2的影响相对较大。

4.1 单因素优化

总结图5～7中的质量、应力和位移的变化规律，获得理想结构的优化参数：上支柱腹板高度M1=10 mm、上支柱翼缘厚度N1=10 mm。应力极值点左侧的应力值偏大，右侧的质量偏重，故优选此极值点（支柱高度H1=350 mm、内支撑宽度B2=350 mm）。

因此得到初步优化结果（表6），与原方案相比，优化后双井架的质量降低15.92%，最大应力降低6.80%，最大位移降低12.07%。

4.2 多目标优化

在利用单因素法初步优化后，考虑各因素之间的交互响应，进行响应曲面多目标优化。

4.2.1 数学模型

结构参数影响研究中表明，M4、N4、B2对质量的影响较大，M3、N3对应力的影响较大。因此基于初步优化参数（B2已优选），以M3、N3、M4、N4为设计变量，双井架的质量、最大应力和最大位移为目标函数建立数学模型：

设计变量：

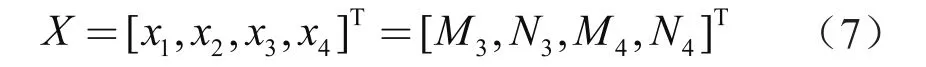
约束条件：

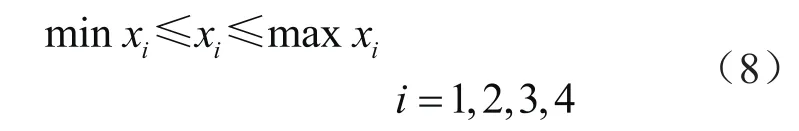
目标函数：

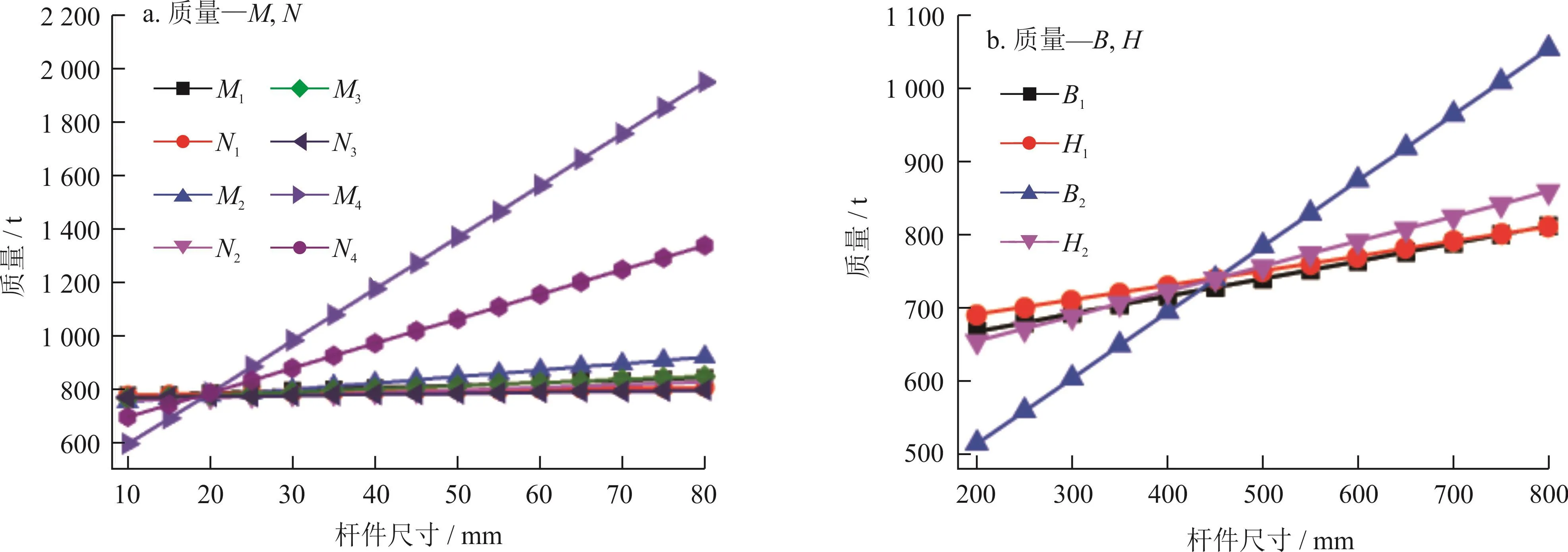
图7 杆件截面参数对双井架质量的影响图

表6 初步优化结果表

利用加权因子W1、W2和W3，将目标函数表示为：

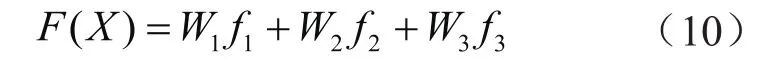
图5-a～b中已确定M3、N3的取值范围为30～70 mm。M4、N4对应力影响较小，在仅保证质量轻的情况上，将M4、N4的范围缩小在初始值30 mm以内。故设计变量X的下限和上限分别取[30,30,10,10]T和[70,70,30,30]T。

4.2.2 试验点计算

采用响应曲面法（RSM）实现优化设计，需要大量的设计变量试验点，获取试验点的方法主要有复合中心试验点法（CCD）、Box-Behnken试验点法（BBD）和均匀设计法等，其中复合中心试验点法比其他方法产生的试验点多，试验数据回归方程精度高，具有可旋转、模型性稳健等特点[19]。

因此选用中心复合试验点法在Design-Expert设计软件中生成30组设计变量的试验点，分析30个双井架有限元模型，计算结果如表7所示。

4.2.3 响应曲面拟合与验证

对试验结果进行拟合，得到质量、最大应力、最大位移三者与设计变量之间优化函数式：

对优化函数的结果进行误差验证。质量、最大应力和最大位移的误差分别在0.2%、1.5%和1.4%以内，说明该优化函数能可靠、快速的预测其他数据组合点的响应值，提供合理的优化结果。

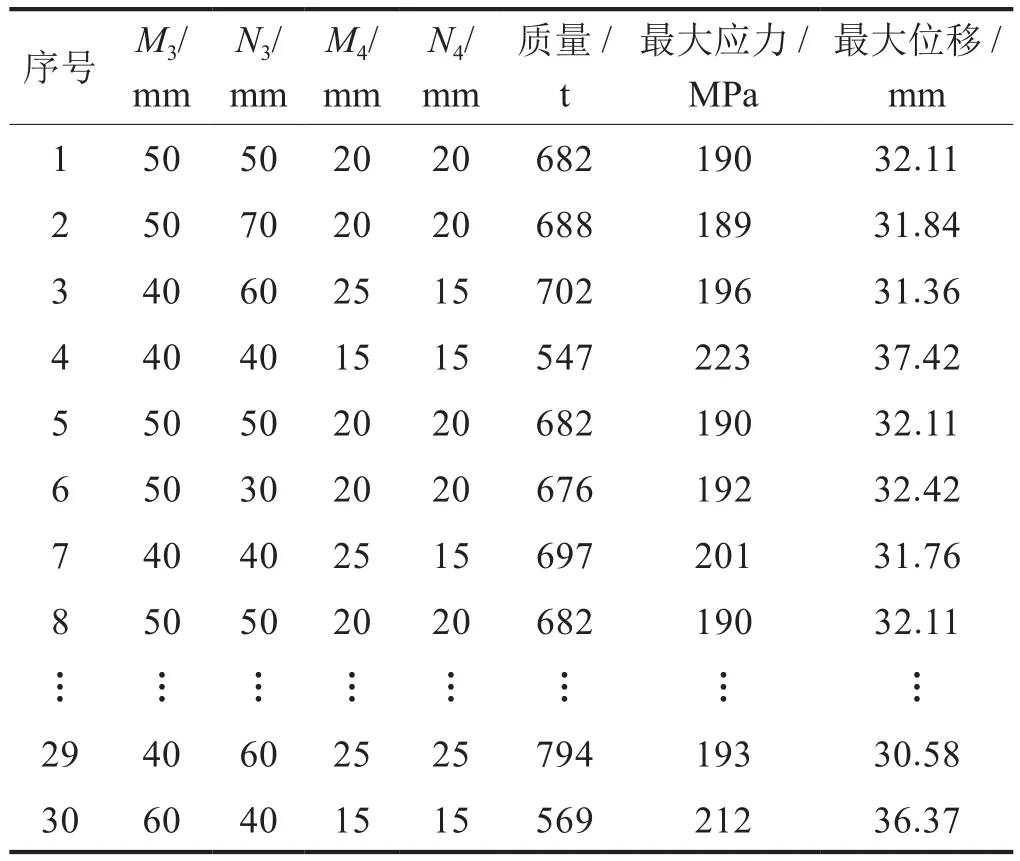
表7 试验点有限元计算结果表

4.3 不同权重下优化结果的误差验证

选取质量、最大应力和最大位移不同的权重（W1/W2/W3=0.538/0.231/0.231,0.33/0.33/0.34,0.25/0.375/0.375），分析得到不同的优化结果（表8）。与本文文献[8]（W1/W2值一致）中质量、最大应力的优化结果误差作对比（图8）。由图8可知，3种加权因子下的结果误差小于文献[8]中的误差，且最大值小于2.7%，验证了单因素与响应曲面法结合的多目标优化的可靠性。

4.4 基于等强度设计的最优结果

在得到不同加权因子（W1/W2/W3）下不同的优化结果后，结合等强度原则，以不同高度段的应力差异最小为目标，获取最优的杆件截面参数组合。

图2已将双井架从低到高分为6段。分析得到不同加权因子下6个高度段的最大应力，如图9所示。由图9可知，随高度升高，不同加权因子下最大应力的变化趋势一致，均呈线性递减。因此，在设计双井架时，偏向从低到高考虑杆件截面强度，有利于提高材料利用率。

在不同加权因子W1/W2（W2/W3=1）和W1/W3（W2/W3=1）下，分析不同高度段应力的最大偏差率（Pmax），如图10所示，Pmax随W1/W2和W1/W3增大而增大，增幅随之增大，在W1/W2=5/5和W1/W3=4/6之前的变化基本平缓。因此在避免因质量权重W1过小而导致双井架过于笨重的情况下，取W1/W2/W3=0.286/0.286/0.428(W1/W2=5/5，W1/W3=4/6)为最优结果的加权因子。

表8 不同加权因子下优化结果表

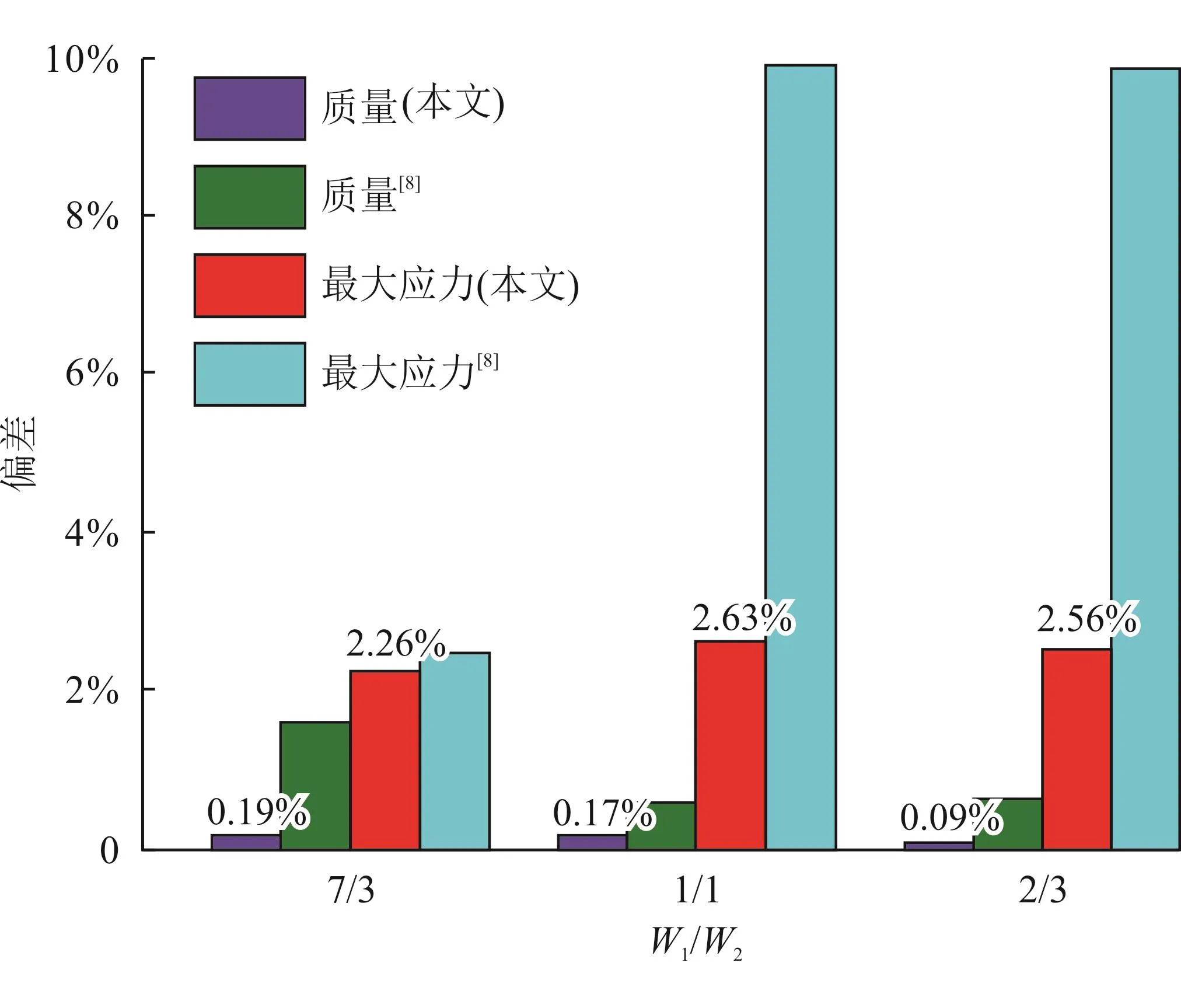
图8 优化结果误差图

图9 不同权重下各高段的最大应力图

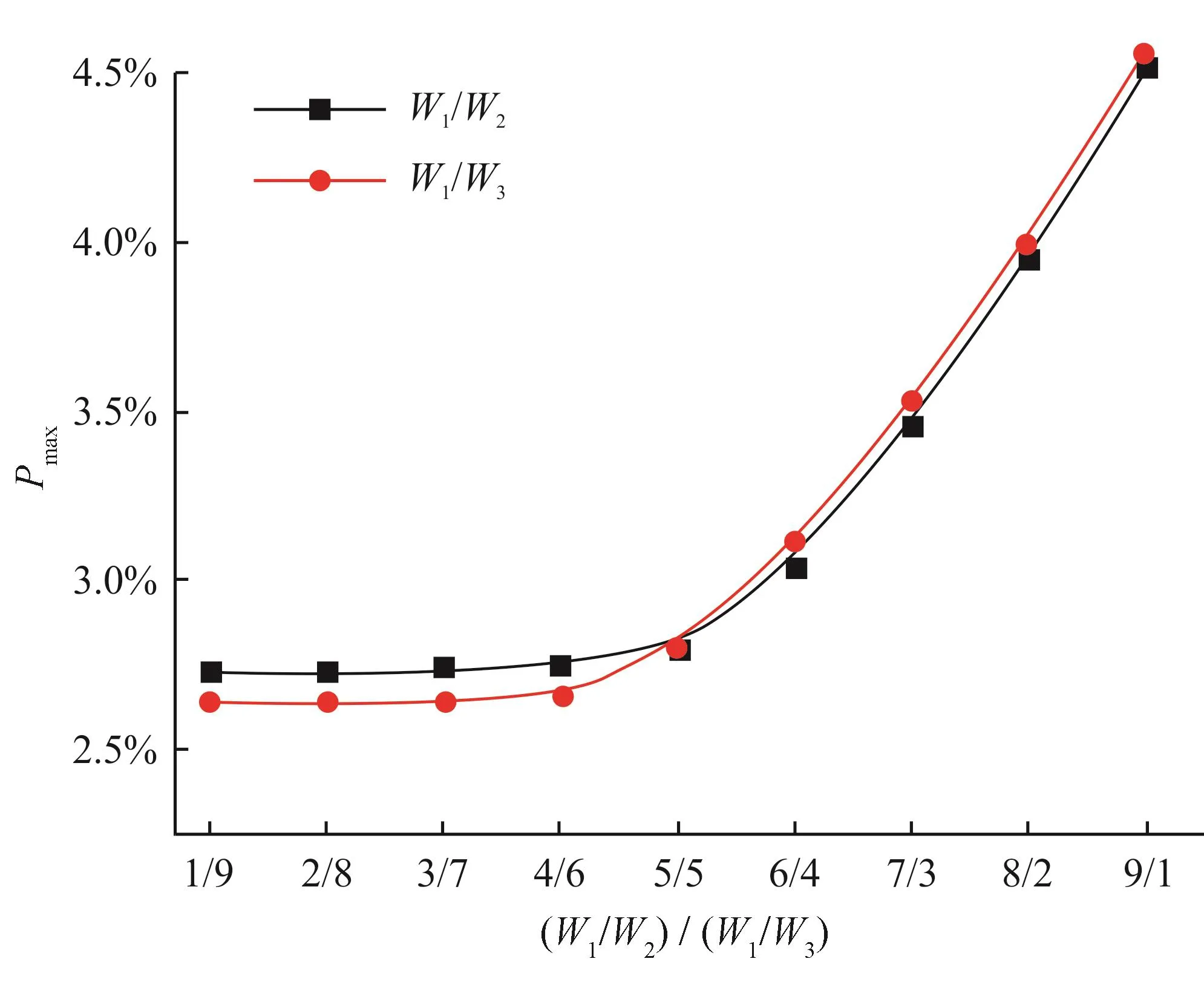
图10 不同权重下的各高度段应力最大偏差率图

将优化前后结果作对比，如表9所示，双井架最优方案较原方案质量降低16.18%；最大应力降低29.25%， 安全系数（2.00）大于API Spec 4F-2013规定[17]的1.67；最大位移（30.62 mm）降低29.35%，小于规范[18]允许值l/400=31.375 mm；不同高度段应力的Pmax降低67.67%，仅为1.18%，在满足强度、刚度要求下提高了材料利用率。

表9 优化前后对比表

4.5 典型工况校核

对双井架最优方案在工况A～D（风载180°入射、－X向水平惯性加速度、－Y向垂直惯性加速度）进行校核（表10）。在各典型工况下双井架的最小安全系数（2.18）大于API Spec 4F-2013规定[17]的1.67，最大位移（26.94 mm）小于规范[18]允许值（31.375 mm），不同高度段应力的最大偏差率（Pmax）小于0.92%，在满足强度、刚度要求下提高了材料利用率，优化结果可靠。

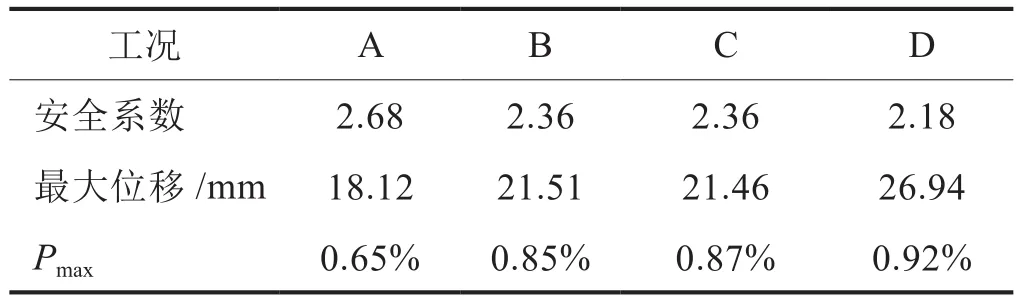
表10 典型工况校核表

5 结论

1）本次优化设计为双井架杆件截面参数优选提出了参考，以引导双井架强度、刚度的设计。

2）随高度升高，双井架应力减小。在设计双井架时，偏向从低到高考虑杆件截面强度，有利于提高材料利用率。

3）最终优化后的双井架满足各典型工况强度、刚度要求，较原方案质量、最大应力、最大位移和不同高度段应力的最大偏差率分别降低16.18%、29.25%、29.35%、67.67%，并验证了优化结果误差小于现有文献的误差，说明单因素与响应曲面法相结合的等强度多目标截面参数优化对双井架结构参数优选和相关井架设计具有指导意义。