瞬变电磁的逆时偏移成像方法
2021-01-06陈紫静陈清礼
陈紫静,陈清礼
(1.中国石化西北油田分公司采油一厂,新疆 轮台 841600; 2.长江大学 油气资源与勘探技术教育部重点实验室,湖北 武汉 430100)
0 引言
瞬变电磁测深法(TEM)是一种时间域电磁法[1],在多个领域得到应用[2-12]。按照观测方式,常用的有中心回线瞬变电磁法、大定源瞬变电磁法和长偏移距瞬变电磁法。TEM是一种人工场源方法,与天然场源方法相比,优点是信噪比高,缺点是理论复杂,资料处理和反演的难度非常大,因此亟待提高资料处理解释和反演的水平[13-14]。对于瞬变电磁法的反演而言,主要还是基于视电阻率概念而展开的,以前主要应用晚期视电阻率,最近十多年来,许多学者展开了全区视电阻率的研究[15-18]。研究人员基本上是沿着3条路线展开反演研究,其一是瞬变电磁法的视电阻率转化成大地电磁测深的等效视电阻率,再利用大地电磁测深的反演理论[19-21],这条路线是在频率域中进行的;第二条路线是在时间域中进行反演[22],如烟圈反演途径;第三条路线是在时间域中直接进行偏移成像[23-24]。前人提出了瞬变电磁场拟波动方程偏移成像,由于大地中的电磁场主要服从扩散方程而不是波场方程,因此该方法需要进行波场变换,再基于波动方程进行偏移成像,理论与过程都比较复杂。与前人的成像方法不同,本文的研究表明大地中的电磁波传播速度比较慢,基于这个特性,设计了一种逆时偏移成像算法,该算法简单直观,且无需进行大量的计算,实践表明效果比较理想。
1 大地中电磁波的速度
逆时偏移成像的一个主要影响因素是电磁波的传播速度,如果速度太大,走时太小,与资料采集时的采样率不匹配,无法进行逆时偏移成像,因此逆时偏移成像能否用于电磁法中取决于电磁波的速度。真空中电磁波的速度(即光速)是300 000 km/s,30 m距离的走时是10 ns,对于1 μs采样的数据来说,分辨地层的能力太差。但是,我们的研究表明电磁波在大地中的传播速度远低于光速,这就为利用逆时偏移成像技术提供了基础。
电磁波的传播速度取决于相位因素:
(1)
式中:ω是电磁波的圆频率;μ是介质的磁导率,由于绝大多数岩矿石磁导率与真空中的磁导率μ0=4π×10-7H/m相同,因此大地中的磁导率可取真空中的磁导率;ε是介质的介电常数;γ是电导率。电磁波的速度为:
(2)
(3)
式(2)是电磁波速度的精确计算式,而式(3)是忽略位移电流的情况下的电磁波近似速度计算公式。由式(3)可以看出,电磁波的频率越高,电磁波的传播速度越快,电阻率越高,速度也越快。
大地中电磁波的速度主要取决于电阻率和频率。表1列出了不同频率和不同电阻率时电磁波的传播速度。例如:1 000 Hz的电磁波在电阻率为10 Ω·m的介质中传播,其速度是316.23 m/ms,只有光速的千分之一左右。也就是说,1 μs的时间,电磁波走过的距离只有0.32 mm。目前瞬变电磁仪器的采样间隔可达0.4 μs,采样率与速度比较匹配,逆时偏移成像有理论基础。
2 逆时偏移成像算法
下面给出中心回线瞬变电磁测深的一种简洁的逆时偏移成像算法,其基本原理与地震勘探中的逆时偏移成像原理相同[25]。在中心回线瞬变电磁测深条件下,对于地下某个成像点的波场(如电位或垂直磁场分量)值而言,是观测点的发射线框发射的波场按照球面波的形式由发射点传播到成像点的。在某个特定时刻,接收线圈接收的波场值可以看成是由该时刻之前成像点的波场传播到观测点的波场值,这样就可以由某个特定时刻的观测波场值按传播时间计算得到成像点的波场值。之所以说简洁,是因为不是按照波动方程理论而是按照射线理论,按照成像点与观测点之间电磁波的走时,把观测点的波场逆时传播到成像点。逆时传播时,速度的确定非常重要,由于瞬变电磁测深方法的频带具有一定的宽度,而速度取决于频率、电阻率等因素,依据采样定理,采样的频率fs决定了观测数据的最高频率fmax=0.5fs,因此,瞬变电磁测深观测数据的频带范围是[0,fmax]。在电阻率一定的情况下,速度主要决定于频率。本文利用频带范围[0,fmax]内能谱最大对应的频率来计算速度。
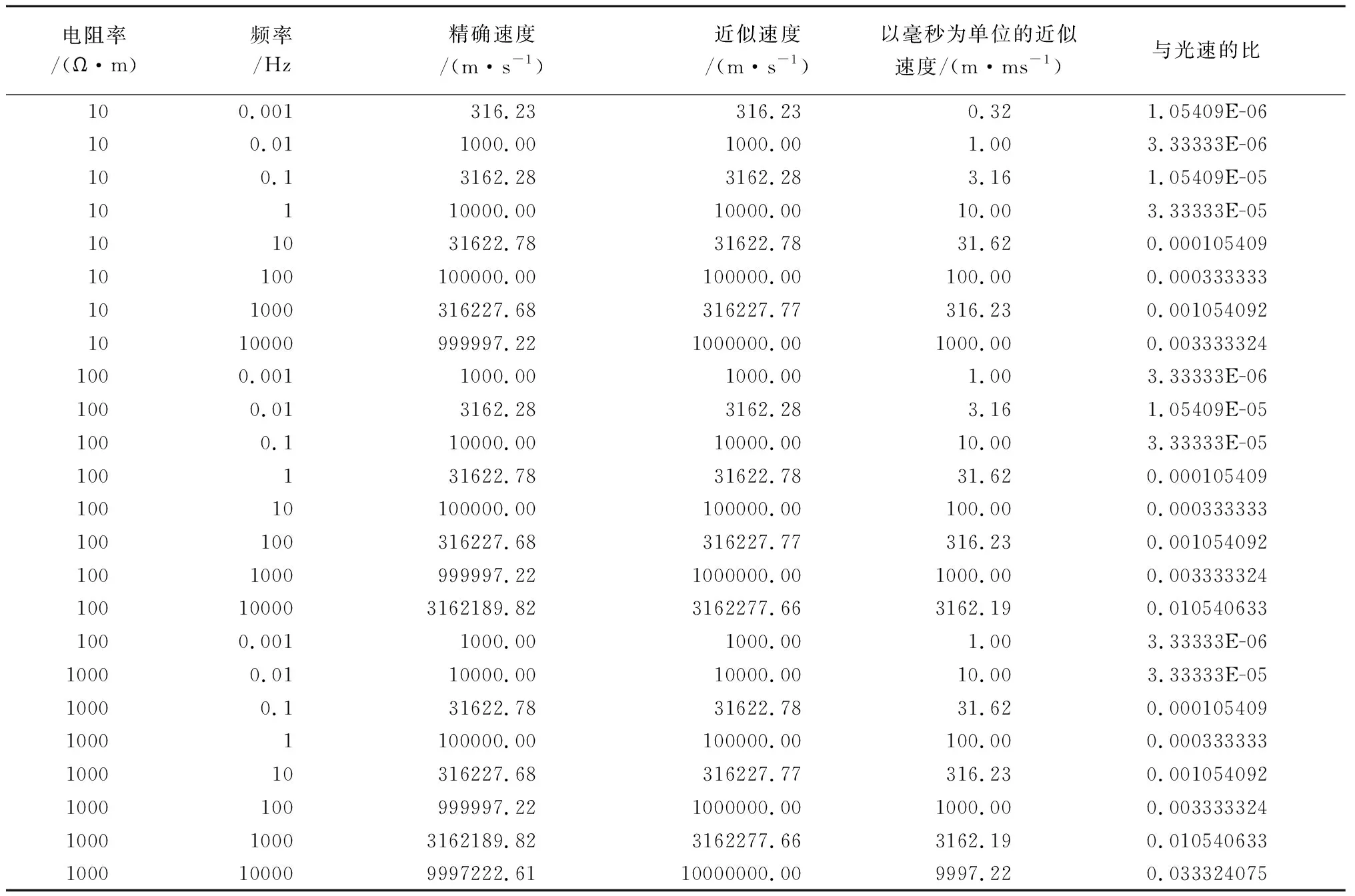
表1 电磁波在介质中的传播速度
1) 算法的输入数据
① 所有观测点的位置数据(u,v),u表示测点距离测线头的距离,v表示测点的高程,单位m。
② 每个测点的观测数据序列(y1,y2,y3,…,yn),观测数据可以是感应电动势、磁场或者电场等波场数据。采样时间间隔deltaT。
③ 成像网格数据,也就是成像点P的坐标(x,z),可按照纵、横方向的步长自动由程序代码产生。
2) 算法的输出数据
所有测点成像点的成像数据 (x,z,F),其中x,z是剖面上成像点的位置,F是成像点的波场数据。
3) 成像算法
① 读取数据,存入数组中:测点A坐标u(i)、v(i),采样时间间隔deltaT,观测数据yobs(i,j);其中i代表测点,j代表时间。
② 设置成像点P坐标x(i,k)、y(i,k),其中i代表测点,k代表深度。
③ 依次计算每个成像点P的波场值F:
a) 计算成像点P到每个测点A的距离R,路程S=2R,时间T=S/V。速度V与电阻率和频率有关,在工区范围不大的情况下,可认为电阻率基本不变,这样速度可以是常数。
b) 根据观测数据yobs(i,j)的开始时刻、采样时间间隔deltaT、时间T找到测点A的对应时间的波场值FA。
c) 由观测点的波场值FA,按照电磁波传播的规律,计算成像点P的波场值FP。具体计算方法视波场采用的参数(感应电动势、垂直磁场)而定。如果波场参数是感应电动势,那么FA=0.5FA; 如果波场参数是垂直磁场,那么FP=0.25FA。
d) 把所有测点在P点的波场值进行叠加,得到成像点P的总波场值F。总波场值是成像点处电磁波波阻抗的间接反映,与地下电性分布直接相关。因此总波场值断面等值线图反映了断面的电阻率分布状态。
④ 把所有成像点的波场值,按照x(距离),z(深度),FA(波场值)输出到数据文件中,再利用等值线绘图软件(如surfer)绘制等值线断面图。
需要说明的是,在均匀半空间中瞬变电磁观测数据具有早强晚弱的衰减特性,在进行偏移成像之前需要进行均衡校正。均衡校正的意义类似于地震勘探中的道数据增益补偿,也就是不同时间采集的数据采用不同的放大倍数进行放大,时间越晚放大倍数越高。由于实践中很难进行精确的均衡校正,文中采用了二代小波变换算法进行均衡校正的替代方案。
3 实测资料的逆时偏移成像
为了检验该算法的有效性,在某煤矿采空区进行了实验研究。以5 m的点距,在一条测线上对10个测点进行了数据采集;采用中心回线瞬变电磁观测方式,发射电流20 A,观测数据是感应电动势,采样时间间隔为0.8 ns,共观测32 000个数据。图1是这10个测点中一个测点的实测感应电动势曲线,总记录时间是24 ms。
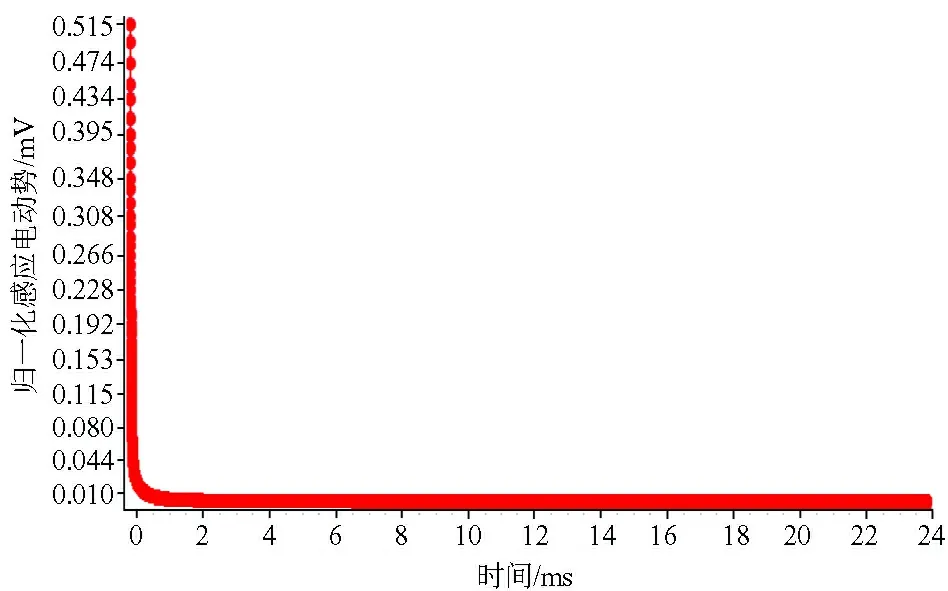
图1 一个测点的实测感应电动势曲线Fig.1 The measured induced electromotive force curveof a site
此时,观测数据的频带范围[0, 0.625×108]Hz,由表1可知,不同频率的电磁波的传播速度不同,需要确定用于成像的平均速度。虽然观测数据的频带范围很宽,但成像时使用的频带范围很窄,具体范围根据勘探目标的最小深度和最大深度来确定,这样平均速度的误差不大。
利用这10个测点的感应电动势数据,首先进行均衡校正,也就是剔除背景值,提取异常数据;而后根据上述逆时偏移成像算法,计算了地下不同位置的波场(即电动势)数据;最后利用得到的地下各个点波场数据,采用surfer绘图软件,绘制出该测线的波场等值线断面(图2)。由图可见,在坐标点(17 m,-15 m)附近有一个低波场异常体,与实际煤矿采空区一致。采空区由于充填地下水而具有低阻特性,理论上说低阻具有低波场值的特性,这就初步说明了本文提出的中心回线瞬变电磁法的逆时偏移成像算法是有效的。
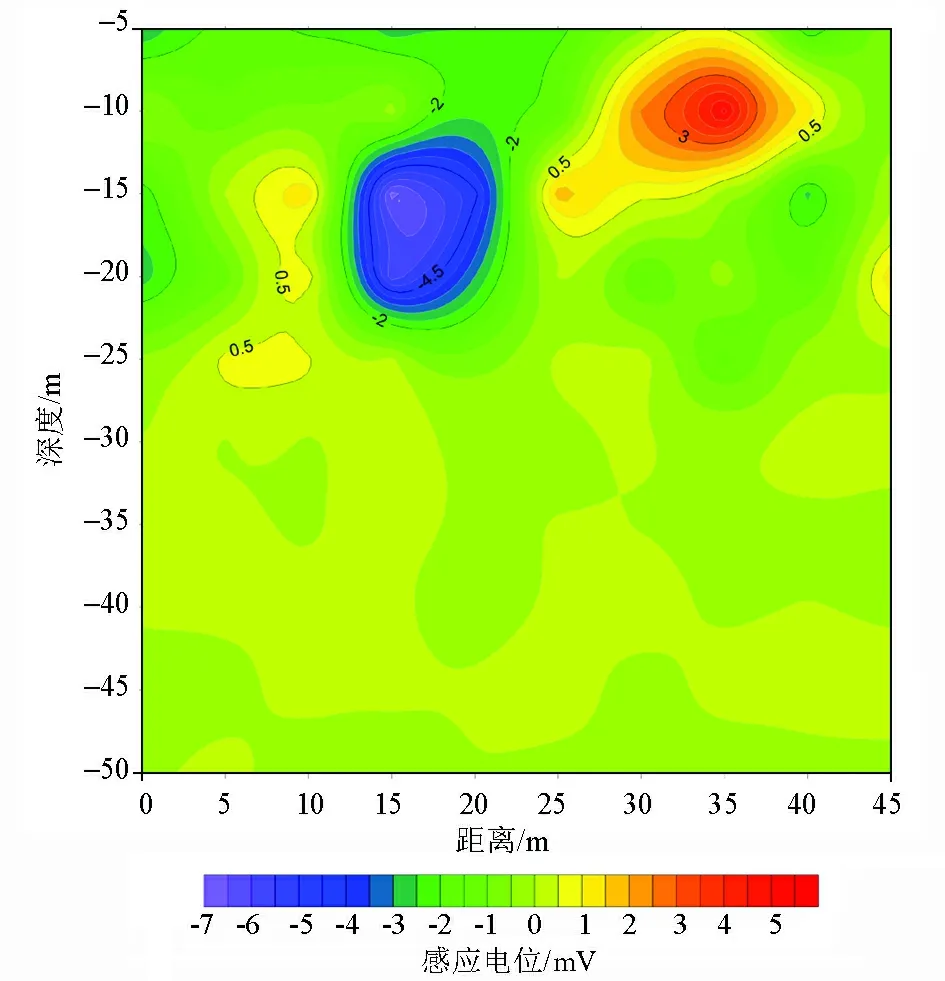
图2 中心回线瞬变电磁法逆时偏移成像断面Fig.2 The inverse time migration imaging section of thecenter loop transient electromagnetic method
4 结论
针对中心回线瞬变电磁法反演十分困难的问题,基于大地中电磁波的低速特性,依据地震逆时偏移成像的基本原理,设计并编写程序代码实现了瞬变电磁逆时偏移程序算法,通过实际验证,该算法能有效揭示地下地质异常体。主要认识有以下几点:
1)大地中电磁波的传播速度与电阻率和频率成正比关系,电磁波的频率越高、电阻率越大,则速度越快。100 Hz的电磁波在电阻率为10 Ω·m的大地中传播的速度是316.23 m/ms,远低于光速300 000 m/ms,只有光速的千分之一左右。
2)由于大地中电磁波速度慢,可对自激自收观测方式的电磁资料进行逆时偏移成像。
3)依据成像点与观测点之间的双程走时,把观测点的波场逆时传播到成像点获得该测点在成像点的波场,把所有测点在成像点的波场进行叠加得到成像点的波场。
4)逆时偏移成像算法的一个关键是速度,在进行逆时偏移成像时,要依据频率和当地的电阻率给出合理的速度参数,而且要用群速度而非相速度。
该方法目前只适用于收发同点的瞬变电磁观测方式,也适合探地雷达资料的偏移成像。发射点和接收点相距很远的观测装置不适用于本方法。
