基于灰色关联模型的针织物热湿舒适性分析与预测

王丽莎，马晓红，孟 花，冯爱芬

(1.河北科技大学 纺织服装学院，河北 石家庄 050018； 2.河北省纺织服装技术创新中心，河北 石家庄 050018)

热湿舒适性指人体在变化的环境中通过热湿传递的作用获得舒适满意度的感觉[1]。织物在人体和环境之间形成一个微小气候区作为人体与外界环境热湿传递的中间物，直接影响二者之间的热湿交换，从而影响人体的热湿舒适感。织物的热湿舒适性是一个物理学和生理学的综合问题，是评判服用性能的重要组成部分[2-3]。灰色模型(Grey Model，简称GM)是多变量灰色系统建模方法的基本模型，该模型中包含多个影响因子变量，常用于分析多个影响因子变量对系统行为变量的作用，来确定该系统未来发展的变化趋势，为规划、决策提供依据[4-5]。本文主要运用灰色模型预测针织物的热湿舒适感觉，将织物所测得可能影响织物热湿舒适性的10个指标看作一个灰色系统，运用灰色关联分析法处理数据，计算出10个指标与热湿舒适性加权分值之间的关联程度，确定每个热湿指标的权重系数，最后建立热湿舒适性灰色模型并进行预测。

1 试验部分

1.1 试验材料

由河北吉篙化纤有限责任公司提供的7种针织物作为研究对象，织物中所含艾草改性竹浆纤维和竹浆纤维均为河北吉篙化纤有限责任公司生产。已知纱线原料成分、纱线细度、织物组织，测试了针织物密度、面密度和厚度，其基本规格见表1。

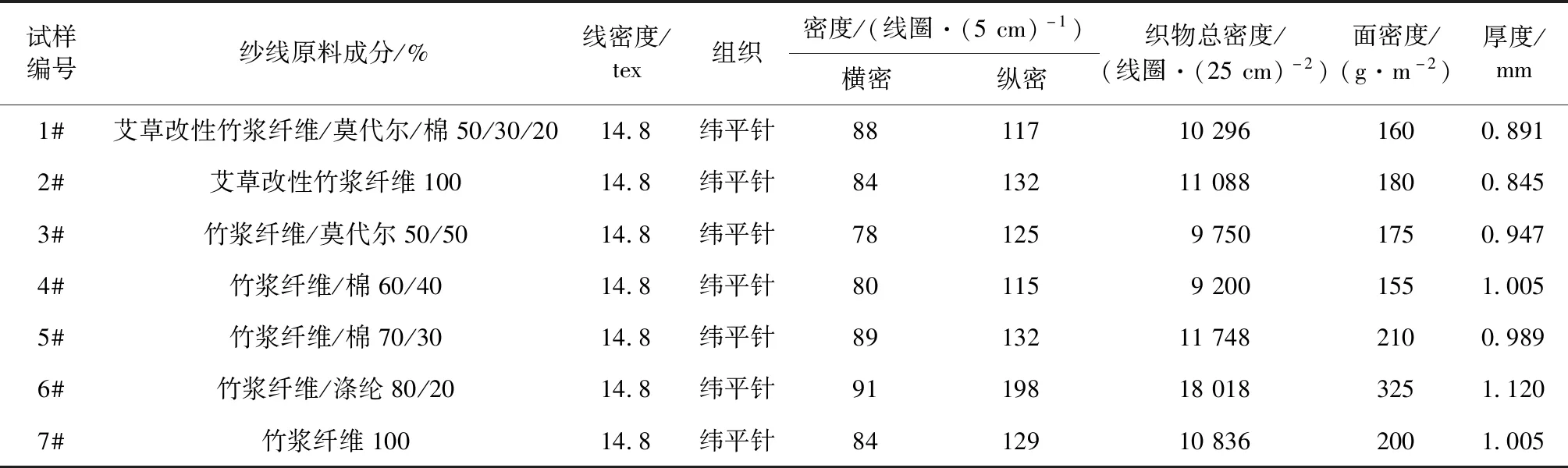
表1 织物规格及结构参数

1.2 织物导热性和接触冷暖感性能测定

采用KES-F7测试仪(日本加多技术有限公司)测试织物的热传导系数和瞬间冷暖感，参照仪器的试验方法，将织物裁剪为20 cm×20 cm，试验前将裁剪好的试样放入恒温恒湿室平衡24 h，在恒温恒湿的条件下进行测试，每种织物测试3次，取其平均值。

1.3 织物透气性测定

采用YG461E型数字式透气量仪(宁波纺织仪器厂)，参照GB/T 5453—1997《纺织品 织物透气性的测定》,将织物裁剪为30 cm×30 cm，试验前将裁剪好的试样放入恒温恒湿室平衡24 h，试验面积为20 cm2,压强100 Pa，每种织物不同部位测试10次，取其平均值。

1.4 织物透湿性能测定

采用YG601型电脑式织物透湿仪(宁波纺织仪器厂)，参照GB/T 12704.2—2009《纺织品 织物透湿性试验方法 第2部分：蒸发法》，将织物裁剪为直径7 cm的圆形试样，试验温度37 ℃，相对湿度50%，时间1 h，每种织物测试3次，取其平均值。

1.5 织物回潮率性能测定

采用Y(B)802G型八篮恒温烘箱(温州大荣纺织仪器有限公司)，将织物裁剪为30 cm×30 cm，试验前将裁剪好的试样放入恒温恒湿室平衡24 h达到吸湿平衡并称量，质量记为G，再将试样放入105 ℃的烘箱中放置2 h，记录质量为G0，按式(1)计算织物回潮率W，每种织物测试3次，取其平均值。

(1)

式中，W为纺织材料的回潮率，%；G为纺织材料的湿质量，g；G0为纺织材料的干质量，g。

1.6 织物导水性能测定

采用YG(B)871型毛细管效应测定仪(温州大荣纺织标准仪器厂)，参照FZ/T 01071—2008《纺织品 毛细效应试验方法》,将织物裁剪为250 mm×30 mm，横向和纵向各3块，试验前将裁剪好的试样放入恒温恒湿室平衡24 h，水温27 ℃，记录30 min后液体沿试样上升的高度值。

1.7 主观服装热湿舒适性测定

将7种面料分别制成160/84 A同一款式同一规格的普通无袖运动背心，挑选14名纺织服装专业女生，年龄为(23±2)岁，体重为(50±3)kg,身高、体重都符合GB/T 1335.2—2008《服装号型 女子》女性的标准中较为普遍的Y体160/84A的要求。试验前将服装放置在恒温恒湿的坏境中平衡24 h。测试条件：温度为35～37 ℃，相对湿度46%～50%，运动15 min，运动结束后在恒温恒湿的环境中休息10 min后进行热湿舒适性评分，最小值评分值为0，最大值评分值为100。

2 试验结果与分析

2.1 试验测试结果

根据前文方法对试样进行测试，试验测试结果如表2所示。由表可知，织物在各方面的性能优劣不同，很难根据某一项具体指标作整体热湿舒适性评价。此外，由于数据规律分布不明显并且数据量少，用传统的确定性数学进行分析很难得出有效的结论。因此，本文引用模糊数学中的灰色理论系统建立灰色关联模型更好的预测针织物的热湿舒适性感觉。

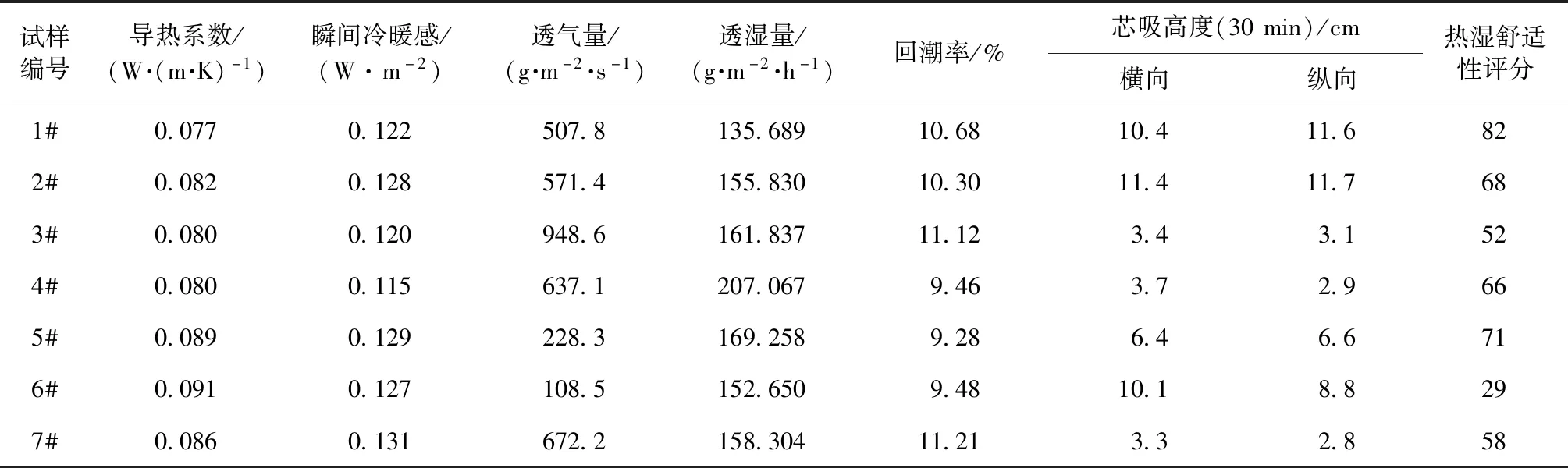
表2 织物热湿性能测试值

2.2 灰色关联分析

2.2.1 灰色关联度

灰色关联分析的原理是根据序列曲线几何形状的相似程度来判断其关系是否紧密，曲线越接近，相应序列之间的关联度就越大，反之就越小[6]。

设x0=(x0(1),x0(2),…,x0(n))={x0(k)|k=1,2,…，n}为系统参考序列，xi=(xi(1),xi(2),…,xi(n))={xi(k)|k=1,2,…，n}(i=1,2,…,m)为比较序列。而灰色综合关联度即体现了折线x0和xi的相似程度，又能反应x0与xi相对于始点的变化速率的相近程度，是一个较为全面地表征序列之间联系是否紧密的量。灰色综合关联度求解过程如下[7]：

均值化：

(2)

求差序列：

(3)

求两级差：

m=minimink|x0(k)-xi(k)|为两级最小差，M=maximaxk|x0(k)-xi(k)|为两级最大差。

求关联系数：

(4)

式中ρ为分辨系数，ρ∈(0,1)，本文取ρ=0.5。

求关联度ri：

(5)

ri反映了比较数列xi与参考数列x0的相关程度，ri值越大，表示二者的关系越密切，说明比较数列xi对参考数列x0的影响因素越大[8]，通过灰色关联度分析，找出对织物热湿舒适性影响程度大的因素作为主要因子。

2.2.2 关联度求解

将针织物的基本参数、物理指标看作一个灰色系统，热湿舒适性加权评分分别为参考数列，记X0=(x0(1),x0(2),…,x0(7))针织物的基本性能与物理性能为比较数列，记Xi=(xi(1),xi(2),…,xi(7))，i=1,2,3，…，10，即X1为总密度，X2为面密度，X3为厚度，X4为导热系数，X5为瞬间冷暖感，X6为透气量，X7为透湿量，X8为回潮率，X9为横向芯吸高度，X10为纵向芯吸高度。由式(2)～(5)计算关联系数和关联度，计算结果见表3。

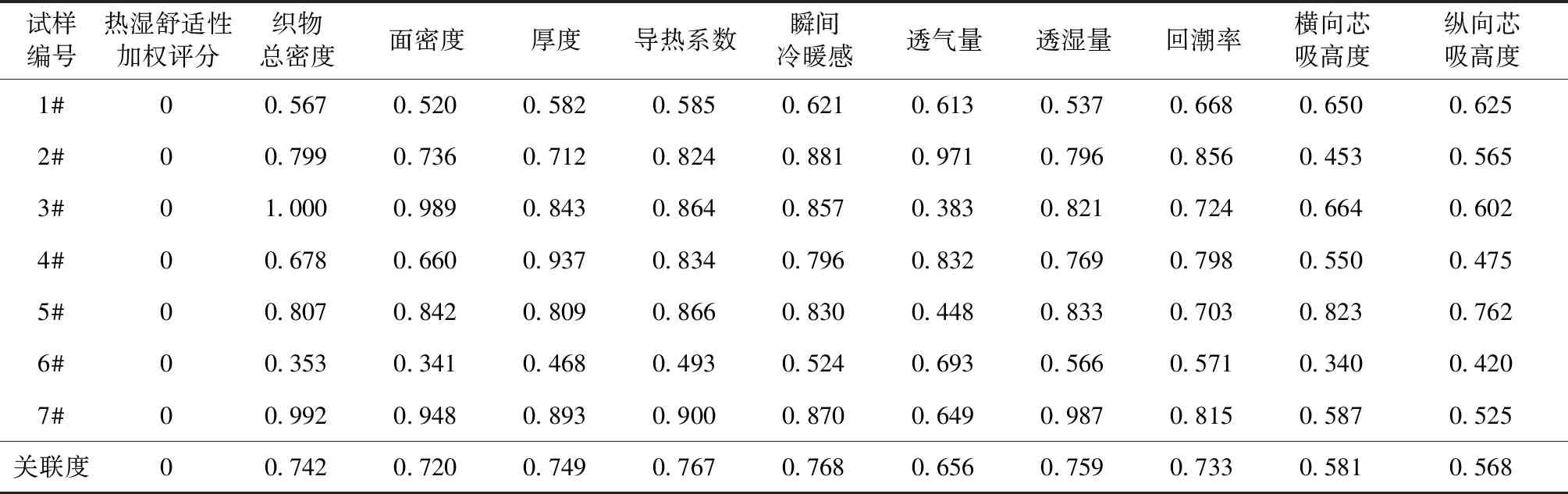
表3 关联系数和关联度

从表3可以得出，面料性能与热湿舒适性之间的关联度大小排序：瞬间冷暖感>导热系数>透湿量>厚度>织物总密度>回潮率>面密度>透气量>横向芯吸高度>纵向芯吸高度。根据表3可知，7种针织物各热湿舒适性之间的关联度均在0.55以上，表示这10个性能指标均可在某种程度上影响针织物的热湿舒适性。为了更好地研究针织物的性能与热湿舒适性之间的关系，将排名前4位的看作是预测模型中的主要影响因素，因此关联系数较大的热湿舒适性能因素依次为瞬间冷暖感、导热系数、透湿量、厚度。

2.3 针织物性能的灰色关联模型

针织物的热湿舒适性受多个指标的影响，而在灰色系统模型中GM (1,N)模型适用于对多数组变量的预测，因此可用GM (1,N)模型进行针织物热湿舒适性预测。

2.3.1 GM(1,N)模型理论分析

由上述对针织物性能与热湿舒适性的关联度求解可知，热湿舒适性与瞬间冷暖感、厚度、回潮率、透湿量相关，通过使用灰色预测理论建立GM (1,N)模型来实现针织物热湿舒适性之间的预测，建模步骤如下[8]:

① GM (1,N)模型是由N个变量组成的一阶线性动态模型，其微分方程为：

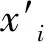
(6)

其中

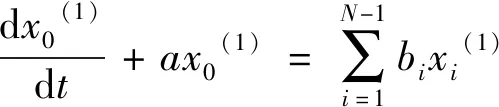
(7)

(8)

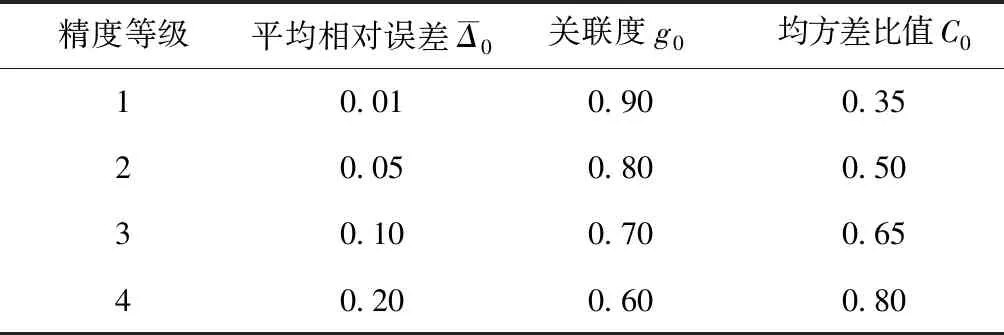
表4 灰色模型预测精度等级标准

2.3.2 建立热舒适性预测模型

原始数据序列为Xi={xi(1)，xi(2)，…，xi(n)}，其中i=0，1，2，3，4,n=1，2，3，…，7，X0=热湿舒适性加权分值，X1=厚度，X2=导热系数，X3=瞬间冷暖感，X4=透湿量，生成序列见表5。

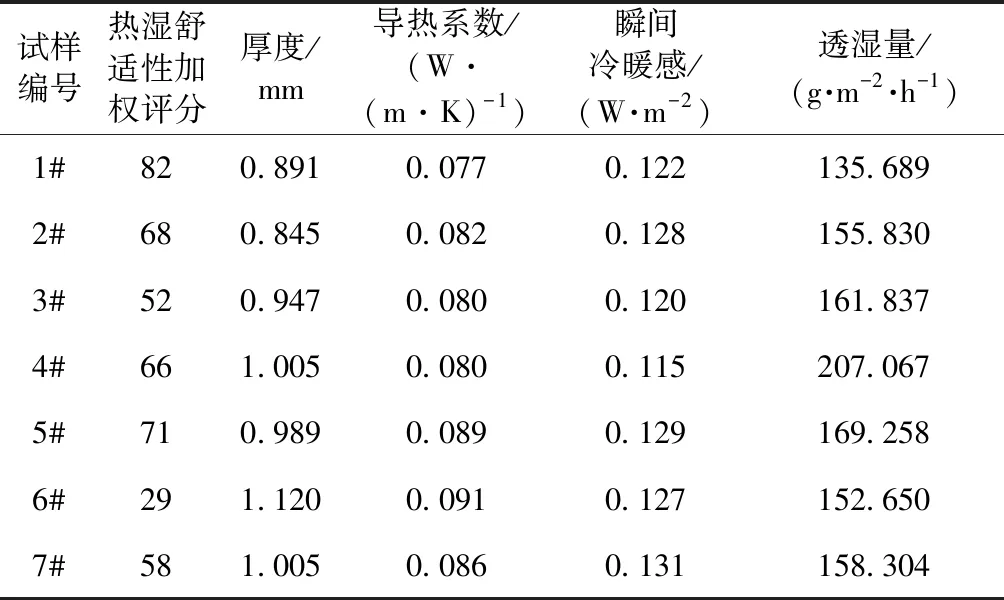
表5 生成序列

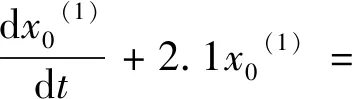
3 869.8x3(1)+1.2x4(1)

(9)

由式(7)可得GM(1, 5)模型的解为：

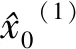
(10)

模型精确度验证：分别取k=0,1,2，…，6。结合式(8)和式(10)计算得到模型残差检验的各项指标见表6。

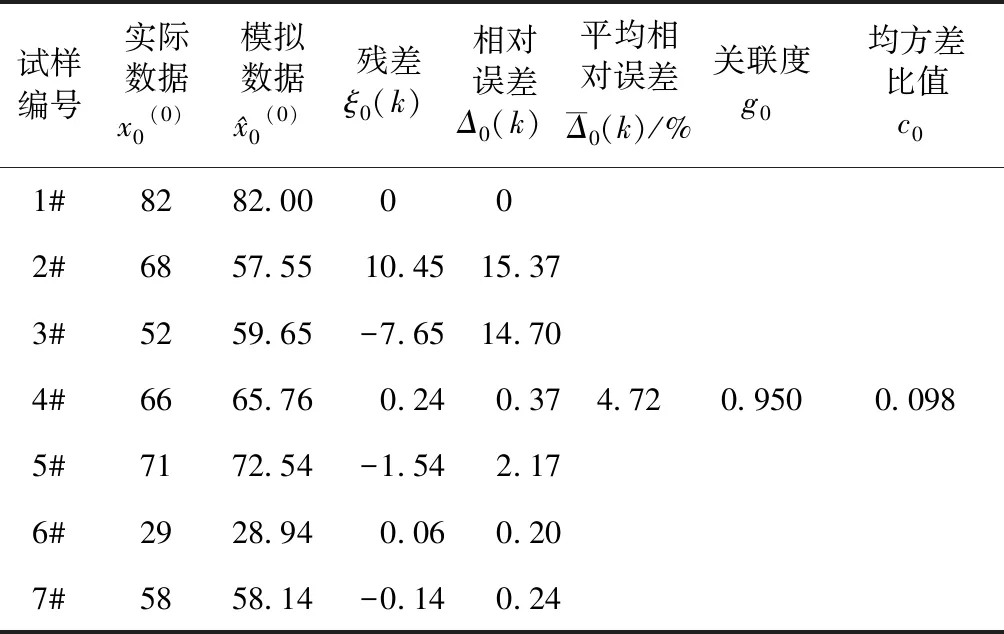
表6 残差检验

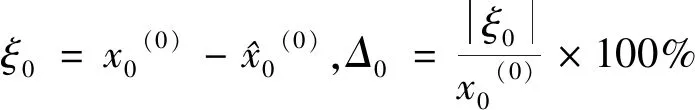
由表6可知模型模拟值与实际值比较接近。相对误差控制在5%以内的有5个，占总体的71.43%；控制在5%～15%之间的有2个，占总体的28.57%。根据表4灰色模型预测精度等级标准平均相对误差为4.72%，大于二级精度；关联度为0.950，为一级精度；均方差比值为0.098，为一级精度，表明此模型模拟数据与实际数据具有较高的相关度。

2.4 模型应用

对艾草改性竹浆纤维/涤纶(84/16)面料进行测试，测试结果见表7。

表7 织物测试数据

取k=0，将表7中的织物测试参数分别代入式(10)计算得出织物的热湿舒适性评分为63.88。由此可知此织物热湿舒适性相对较好，可以应用于服装中，为消费者提供更多的选择。

3 结 论

通过灰色关联度分析，结果显示织物性能与热湿舒适性之间的关联度大小依次为瞬间冷暖感、导热系数、透湿量、厚度、织物总密度、回潮率、面密度、透气量、横向芯吸高度、纵向芯吸高度。

对影响因素较大的影响因子瞬间冷暖感、导热系数、透湿量、厚度与热湿舒适性建立了GM(1, 5)关联模型，模型与实际预测值具有较高的相关度，从而在得知织物的瞬间冷暖感、导热系数、透湿量、厚度的情况下实现对织物热舒适性的预测分析，节省了试验量，提高了工作效率。