考虑流固耦合的任意支撑冷却水管路 机械阻抗计算方法

郑军林，李艳华，吴 炜，王 振

（1.海装驻武汉地区第二军事代表室，武汉430064；2.中国舰船研究设计中心，武汉430064）

0 引言

冷却水管道广泛存在于船舶动力系统中，管路系统的流体脉动和结构振动不仅会损坏管路和设备等，还会对水下辐射噪声，对其隐身性产生影响。最初对流体管道振动进行研究，是来自于对横跨阿拉伯输油管道的振动分析[1]。近些年，国内外研究者建立了多种流体管道考虑流固耦合的理论模型，其中如流体管道4方程理论模型[2-4]、6方程理论模型[4]、8方程理论模型[5-6]以及14方程理论模型[7]。但在目前的国内外研究中，对管道支撑的考虑，主要以固支以及自由支撑为主，形式相对比较简单。而船舶动力管路系统管路的支撑形式包括固定支撑、简支支撑以及弹性支撑等多种支撑形式，不同的支撑形式，管路系统的振动噪声特性也会完全不同。

同时阻抗是振动噪声领域中广泛适用于分析的一个特征参数，通过阻抗可以掌握振动传递特性，并可针对性地采取有效控制措施。因此，本文建立考虑流固耦合的任意支撑冷却水管道机械阻抗的计算方法，本篇研究主要以管路中常见且大量存在的直管为研究对象，解决直管道的阻抗计算，为船舶动力系统冷却水管路机械阻抗计算以及振动噪声控制提供技术支撑。

1 冷却水管道动力学模型

图1为冷却水管道示意图，假定其与水平面之间的夹角为α，x、y、z坐标如图1所示。其中：w为管壁线位移，θ为管壁角位移，f为管道内力，m为管道弯矩，At为管壁横截面面积，P为冷却水压力脉动，V为冷却水速度，Al为冷却水横截面面积，ρ为冷却水密度，K为冷却水体积模量，k为剪切分布系数，G为管道剪切模量，υ为泊松比，e为管道壁厚，R为冷却水截面半径。

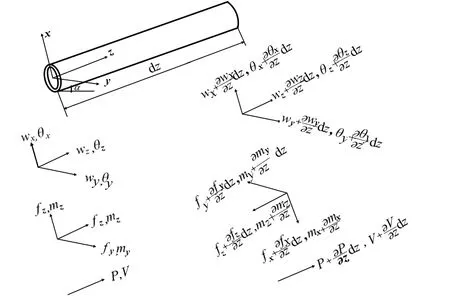
图1 冷却水管道简化模型

1.1 冷却水管道流固耦合模型

根据流体力学、理论力学推导，得到14 方程冷却水管路流固耦合模型[8]，14方程模型包括轴向振动4方程模型、x-z平面振动4 方程模型、y-z平面振动4 方程模型和扭转振动2方程模型。

轴向振动4 方程模型为

1 .2 冷却水管道流固耦合模型求解

1.3 边界条件

冷却水管道的边界简化如图2所示，z＝0、z＝L分别为管道的初始端和末端。冷却水管道支撑简化成6个自由度弹性刚度，如kx0为管道初始端x方向线刚度，ktxL表示管道末端x方向扭转刚度。

图2 冷却水管道边界条件简化模型

2 任意支撑冷却水管路阻抗计算

根据以上理论和求解，通过MATLAB软件编制计算程序，输入管道的物理参数和边界条件，便可对任意支撑冷却水管路阻抗进行计算。

3 冷却水管路机械阻抗计算方法验证与分析

试验模型如图3所示，管道中充满水。用力锤在管道端部分别施加轴向激励和横向激励。从相关模型方程可知，14个参量相互耦合和关联，具有非独立性，因此仅列出部分参量测试结果与计算结果对比，来验证本文计算方法的正确性。

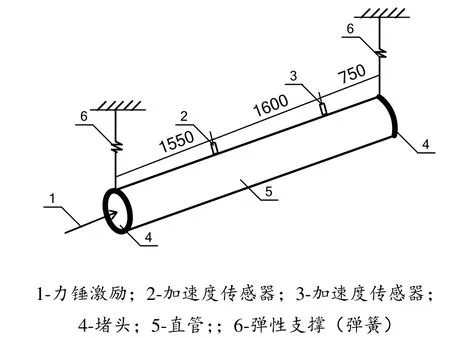
图3 冷却水管道试验台架（单位：mm）

表1为水管路的具体参数。

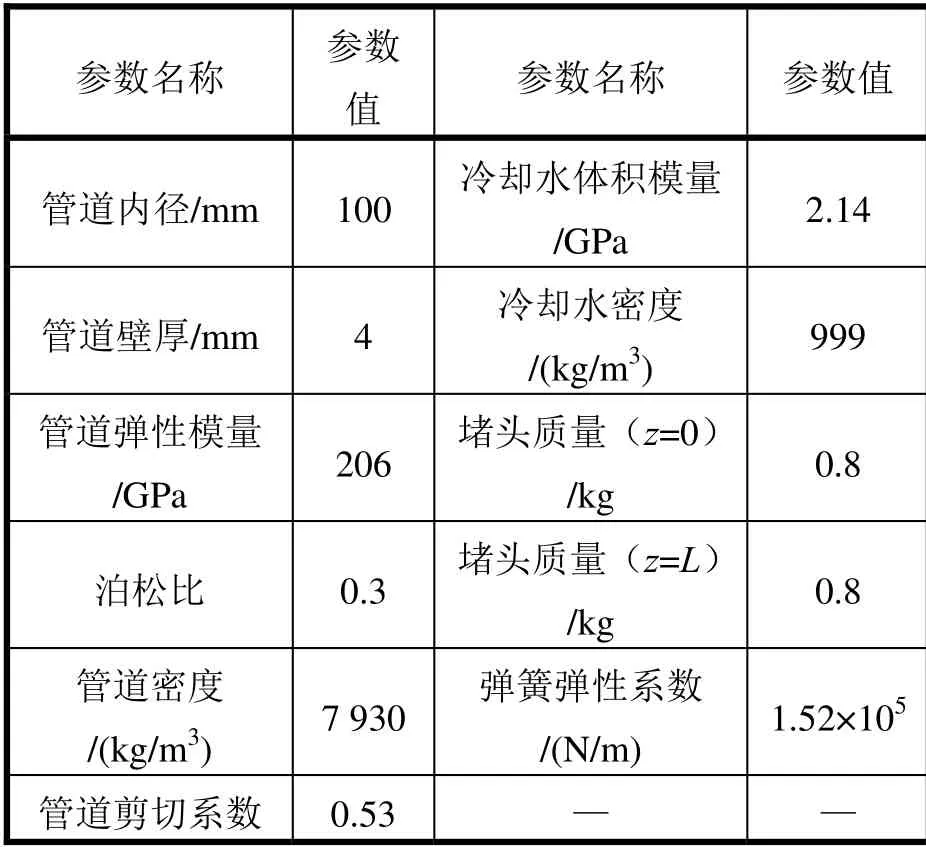
表1 管路和冷却水参数

3.1 轴向振动机械阻抗

如图3所示，在管道端部进行轴向激励，利用3560E 数据采集仪采集数据并处理成阻抗形式，2 号点和3号点的轴向机械阻抗计算和实测值对比如图4所示。

图4 轴向机械阻抗对比

由图4可知，实测值与计算值吻合较好。但在频率大于800 Hz 时，差别稍偏大；通过分析发现，是因为激起了高阶的周向模态，在高于此频率时，管道截面不是圆形，因此称其为叶状波（Lobar Wave）。根据Jong De 周向模数大于1的频率计算公式，本试验管道2 阶周向模态频率约800 Hz，因此大于800 Hz以上激起了叶状波，产生了差别稍大的现象。Jong De在管道试验中，也发现了此现象，计算值和实测值对比在高于750 Hz 时，比低频偏差大很多[10]。

3.2 横向振动机械阻抗

根据图3，在管道一端对管道进行垂直向下的横向激励，利用3560E数据采集仪采集数据并处理成阻抗形式，2号点和3号点的横向机械阻抗计算值和实测值对比如图5所示。

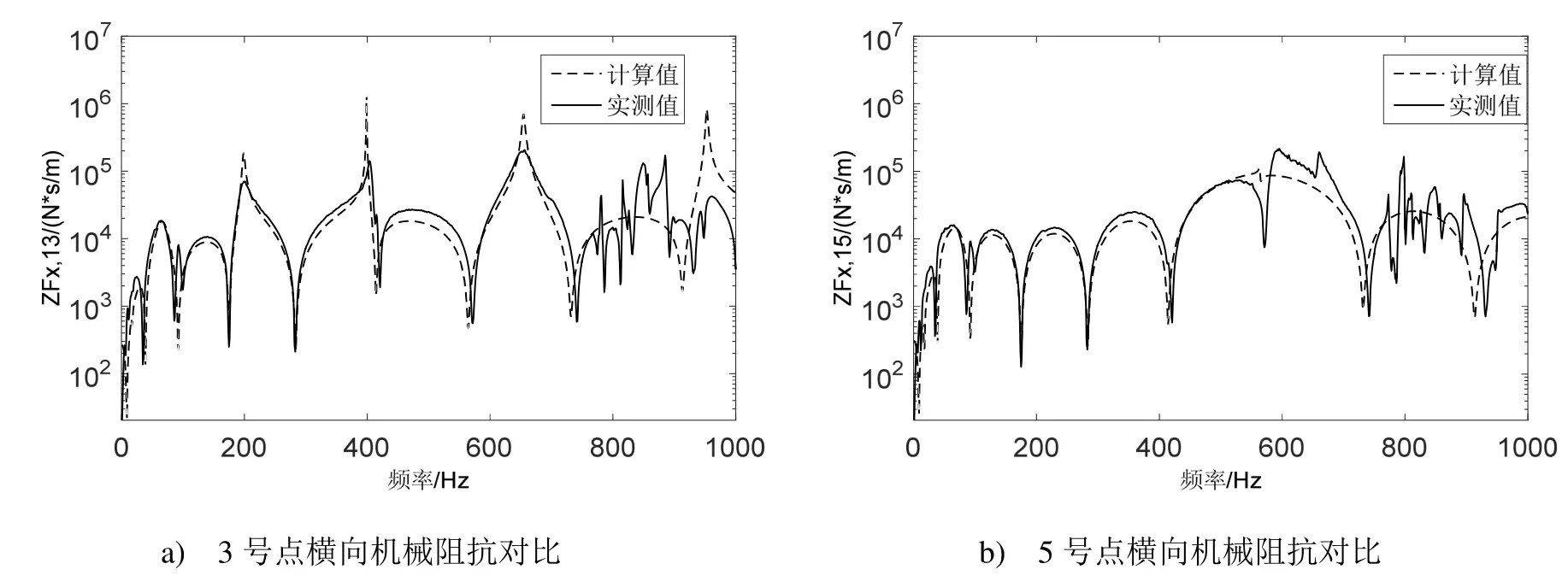
图5 横向机械阻抗对比

从图5可看出，实测值与计算值吻合很好，尤其小于800 Hz频段范围内，基本一致。同样由于激起了高阶的周向模态，在大于800 Hz以上时，偏差较大。

4 结论

本文建立了考虑流固耦合任意支撑冷却水管道机械阻抗的计算模型和方法，通过试验测试，验证了模型和计算方法的正确性，可对任意支撑的流体管道机械阻抗进行计算和分析。同时，通过改变计算模型中支撑和结构等输入参数，利用该方法计算程序，可得到不同方向振动所对应的机械阻抗，利用阻抗可分析冷却水管路的振动噪声特性，进而有针对性的提出振动噪声控制措施。