傅里叶算法暂态特性以及微机保护的动作时间

刘华龙，阮宜菁

（大连船舶重工集团有限公司，辽宁大连 116000）

0 引言

微机保护算法的关键技术途径可表述为：计算体现被保护对象运行方式及特点的物理量参数，包括电压、电流等电气量的有效值和矢量，或算出其基波分量、序分量或某次谐波分量的模值大小及相位大小，并与给定的阈值进行比较[1]。

在微机保护中各个继电器都是由其相应的算法实现的。目前的主流算法都是通过采集输入的电气量，经算法公式计算得到逻辑原理所需的数据，并与定值进行比较。最常用的是傅里叶算法，实现对过流继电器、滤序器和移相器等的数据计算。上述保护算法充分利用微处理器运算速度快、处理速度高的特点，完成传统保护所不能实现的功能[2]。

算法研究的主要问题有2点：准确度和速度（时间窗）。准确度指的是采用微型计算机采样所得到的离散数据点与原始信号在各个采样时刻实际信号在数值上的逼近程度即采集精度。而速度即时间窗表示所用来执行保护算法所需要的数据时间长度，所用时间越长，则保护动作越慢。在一定采样频率下进行离散采样时，故障发生后用于执行保护算法所需的采样点个数被称为此算法所需的时间窗。

不难发现，速度和准确度在同一个保护算法中难以兼顾，是矛盾的关系。因此，研究保护算法的核心就是在准确度和保护速度上进行权衡。此外，微机保护中通常会引入数字滤波器，某些保护仅通过算法可实现，而有些保护则需配合数字滤波器共同工作，数字滤波器所产生的时间延时也会影响保护的速度。因此评价算法时还需综合考虑其对数字滤波器的要求[2]。

1 傅里叶算法

1.1 全周傅里叶算法

式中：N为工频一周波内的采样点数。N确定后，对于特定成分的频率，如对于基波k＝1，式中

1.2 半周傅里叶算法

全波傅里叶算法的有效数据窗为1个周波即20 ms，在某些要求保护动作速度较高的故障情况下难以满足快速性的要求。因此，为了提高保护动作速度，可以采用半波傅里叶算法[3]。半周傅氏算法数据窗为12点，响应速度很快，但无法滤除直流分量，需与差分滤波器一起使用。

其基本点积计算为

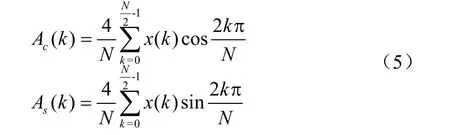
与全波傅氏算法相比，半波傅氏算法不能消除偶次谐波分量（包括直流分量）。因此，在工程应用中，为兼顾继电保护装置的准确性和快速性，多采取如下策略：故障起始时刻进行半波傅氏算法运算提供保护逻辑所需的计算数据，一周波即20 ms后采用全波傅氏算法。

1.3 关于各类傅里叶算法的评述

综合上述分析，在响应时间方面，半波傅里叶算法由于所使用的数据窗口更短，判别故障所需时间就更短，因此保护动作时间更短。但其不能滤除直流分量和偶次谐波分量，对于包含偶次谐波和非周期分量的输入信号源，采用半波算法所计算的数据精度低于全波算法。当追求保护快速性时，应当选用半周傅氏算法（如差动保护、短延时等）；当在临界位置附近时，为提高灵敏度，需要精确计算（如零序过流保护、零序差动保护等），则需选用全周傅里叶算法并使动作速度稍慢一些。

2 过流保护动作时间与返回时间

详细分析由傅里叶算法影响的过流继电器动作时间与返回时间。采用傅里叶算法的过流保护暂态特性如图1所示。

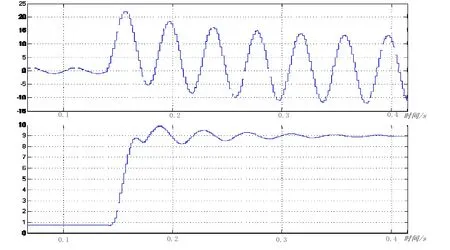
图1 短路电流及傅里叶算法的输出波形

图1为短路电流，图2为傅里叶算法输出。为定量分析傅里叶算法的暂态特性，图1中傅里叶算法的输出可用图2予以抽象。

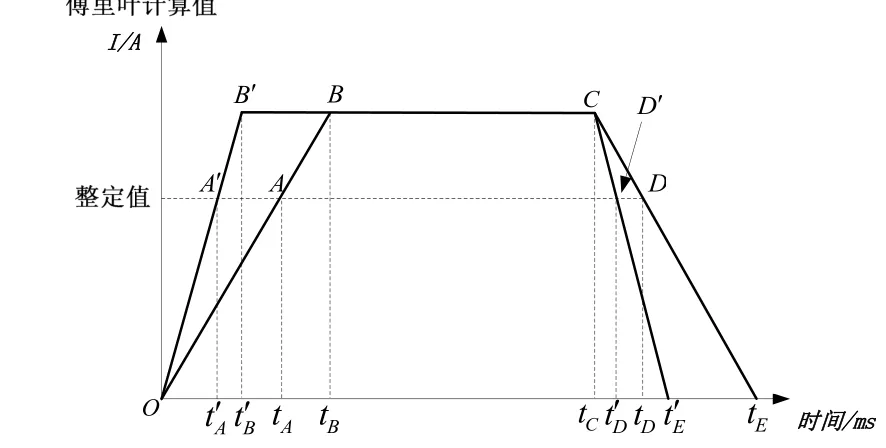
图2 傅里叶算法的过流保护暂态特性图

上述过程中，O点为故障发生时刻，A 点为计算值超过整定值时刻，B点为算法时间窗终止时刻，C点为故障切除时刻，D点为计算值返回时刻，E 点为时间窗终止时刻。A 点、B点、C点、D点对应全周傅里叶算法，A′点、B′点、D′点对应半周傅里叶算法或半周积分法。

图2为近似图形，做出如下假设：

1）去除非周期分量的震荡过程，认为时间窗结束后直接进入稳态。

2）认为过渡过程为线性递增过程。不同的合闸角度导致不同的递增过程，但总体而言，时间窗结束后都能进入稳态。

在上述前提下进行推导，其中tB是时间窗固有常数：对于全周算法，tB＝20 ms；对于半周算法tB＝10 ms。

tA为自故障发生后到计算值超过整定值的时间，不妨称之为上升过渡时间，其大小与故障电流有关，在稳态故障电流为整定值n倍的情况下）

自计算值超过整定值开始计时至计算值进入稳态的时间，不妨称之为稳态过渡时间：

容易知道自故障切除后起到计算值小于返回值的时间也是稳态过渡时间，即

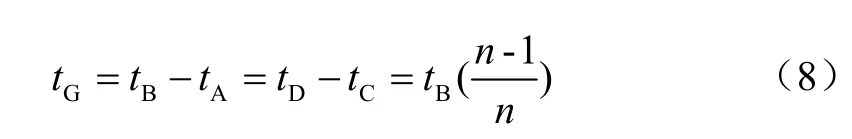
在上述前提下，计算保护的可返回时间tF，即自故障后开始计时，在该时间之前由别处断路器完全切除故障电流，保护装置不会跳闸。在此概念下，故障起始点为O 点，故障切除点位C 点，故可返回时间tF＝tC。

故障完全切除后，保护的数据窗内还剩余一部分故障时的数据，因此计算值无法立刻变为0，存在过渡过程；在此期间，保护内部的计时器会继续计时。因此，欲使保护在此种情况下不动作，必须使得保护计时器起始时刻与保护计时器终止时刻之差值比整定值来得小，即

有时为使动作速度加快，在内部计数时会减去提前量tq，整定值tzd则变为tzd－tq。由于计数时间变短，所以即使动作时间加快了，但可返回时间也相应缩短了

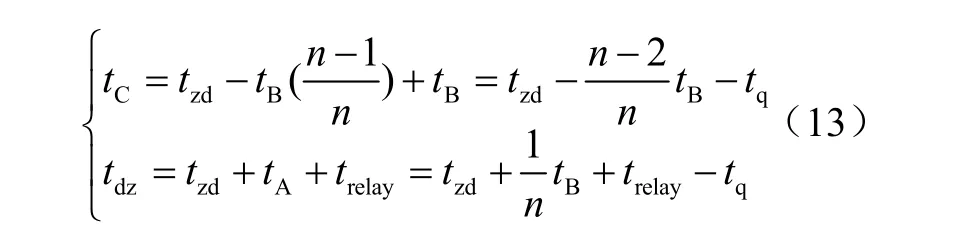
3 结论

通过分析傅里叶算法的暂态特性以及其与微机保护的动作时间之间关系可知：

1）在保护的动作延时中加入内部提前量不能使总体指标变好，因为虽然加快了动作时间，但可返回时间却缩短了。

2）使指标变好的唯一方法是缩短时间窗tB，由于抑制非基频信号的能力是数据窗长度的函数，数据窗越长，抑制能力越强。因此存在精度与速度上的矛盾，必须取舍。

3）故障电流越大，动作速度越快。考核动作时间时应以小电流n＝1.2按标准进行考核，以免保护不能快速动作。故障电流越大，可返回时间越短，故考核可返回时间应以大电流n＝10.0来进行，以免保护不能及时返回。在上述2种极端情况下保护仍能满足时间指标时，可保证过流继电器满足使用需求。