一种表贴式PMSM连续集模型预测转矩控制研究

绳然，曲行行，曾洁

(大连交通大学 电气信息工程学院，辽宁 大连 116028)*

永磁同步电机(PMSM)具有体积小、功率密度高、调速范围大、转矩输出能力强等优点，被广泛应用在运动控制领域[1-2].在永磁同步电机调速系统中，磁场定向控制(FOC)和直接转矩控制(DTC)是最广泛的两种控制方法.

模型预测控制(MPC)方法考虑了控制量对未来状态的影响,具有滚动优化、在线反馈校正等特性.目前PMSM的MPC是通过电机的数学模型预测受控变量的未来状态,基于性能指标来实现电机的最优控制.一些学者将MPC分别结合FOC和DTC，提出了模型预测电流控制(MPCC)和永磁同步电机模型预测转矩控制(MPTC)两大类控制思路.传统DTC通过查表法选择电压矢量，模型预测转矩控制(MPDTC)通过对电机状态进行预测，将预测值代入性能指标价值函数来选择最优电压矢量，在最优矢量选择上更加有效[3].与传统FOC相比，MPCC无需电流环PI参数整定，可以获得更好的动态响应特性[4].

根据电压矢量控制集的不同，MPC可分为有限控制集MPC(FCS-MPC)和连续控制集MPC (CCS-MPC)，FCS-MPC只对有限数量电压矢量进行评价计算，算法相对简单易于实现.CCS-MPC对整个电压矢量可行集进行搜索计算，然后通过空间矢量调制(SVM)输出电压矢量[5-7].对于MPC还有显式和隐式两种控制方法[8]，在显式MPC中，MPC问题离线求解，对于PMSM控制系统，精确的显式模型预测控制对实时计算的要求比较宽松，计算量主要是在相应控制策略中进行查表操作，但对嵌入式存储需求过高.而隐式MPC的主要特点是计算量大,在嵌入式系统上，必须实时解决PMSM的非线性规划问题，隐式MPC在嵌入式系统中需要定制快速的优化求解方法[9].

本文针对SPMSM CCS-MPDTC提出一种基于梯度下降法的有限迭代次数的最优控制方法，根据电机状态时间函数得到电机预测模型，同时证明了SPMSM的转矩和磁链的价值函数是凸函数.采用有限迭代次数的梯度法求取最优解，并使用投影法将其结果限制在可行集内，通过SVM方法输出最优电压矢量.最后通过与FCS-MPDTC进行对比分析仿真，结果验证了其可行性和有效性.

1 模型预测转矩控制系统

1.1 PMSM离散模型

为预测PMSM的未来状态，以d-q旋转坐标系定子磁链为状态变量，通过一阶前向欧拉离散法推导出PMSM的离散时域模型表示如下：

(1)

式中：

(2)

式中,g:R2→R2.x=[ψd,ψq]T；u=[ud,uq]T；ψr=[ψf,0]T.ud、uq，id、iq，分别是d-q坐标系下电压、电流，Ls为定子电感；Rs是定子电阻；Ts是控制周期；ψf是转子永磁体磁链；ωe是转子电角速度；p是电机极对数.

1.2 系统基本原理

永磁同步电机MP-DTC系统原理如图1所示，MP-DTC一般以电磁转矩和磁链误差为控制目标.

(3)

(4)

最后由MPC转矩控制器选取价值函数最小的电压矢量作为驱动信号，逆变器将驱动信号作用于电机.

2 CCS模型预测直接转矩控制

2.1 优化问题描述

在线离散情况下，考虑如式(5)、式(6)的优化问题:

minimizeΔyNTPΔyN+

(5)

subject toxj+1=f(xj,uj)

yj=g(xj)

Δyj=yj-r

Δuj=uj-uj-1

uj∈U

∀j∈{0,1,…,N-1}

(6)

式中，j是预测时域步长；Δy是转矩和磁链偏差；P、Q为权重矩阵，P∈diag(R2×2);Q∈diag(R2×2).式(5)为价值函数，式(6)为系统约束.输出控制序列为U*=[u0*,u1*,u2*,…,uN-1*]T,系统输出取第一个电压矢量u0*.

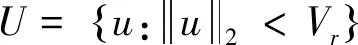
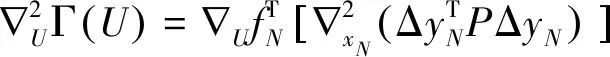
(7)

式中,fj:j=[1,2,…,N]是线性方程，Ufj和即为常数;

(8)

(9)

它的任何局部最优解就是它的全局最优解.所以问题(5)、(6)是一个标准的凸优化问题，即可用标准的数值优化技术求解.

2.2 MP-DTC在线梯度优化算法

本文式(5)、(6)的系统动态方程压缩后得到(10)：

xj(V)=Ajx0+[Aj-1,…,A,I]BV

式中,V=[u0,u1,…,uj-1]T，V∈R2j，xj=fj(V).定义z(V)=[g1(V)…gN(V)]T,Z∈R2N，消除问题(5)、(6)中的状态变量，得到如下静态的标准的优化问题形式：

minΓ(V)=zT(V)Hz(V)

(11)

梯度下降法是求解无约束非线性问题的经典算法，其每一步迭代过程中的计算量都非常小，不需要计算二阶导数，并且对于任意给定的初值经过不断的迭代都能够收敛到稳定点.对于严格的凸函数而言，无约束局部极小点就是全局极小点，并由式(12)唯一确定；

Γ=Hz(U)+z(U)=0

(12)

(13)

算法流程图如图2所示.

2.3 迭代初始值选取

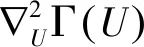
3 仿真分析

基于上述理论分析，所提出的CCS-MPDTC系统如图4所示.为验证所提出CCS-MPDTC的可行性和有效性，利用Matlab/Simulink对传统FCS-MPDTC和CCS-MPDTC进行对比仿真.采样频率选择10kHz.仿真系统具体参数如下：直流母线电压UDC为60 V；额定转速nN为2 000 r/min；极对数p为4；相电阻Rs0.3Ω；电枢电感LS为0.7 mH；转子磁链ψf0.033 Wb；额定转矩Te1.27 N·m；转动惯量J0.000 42 kg·m2，并忽略死区和饱和影响.参考转矩Te*由外环PI调节器产生，参考磁链|ψs*|按最大转矩电流比(MTPA)方法产生，CCS-MPC调节器的迭代起始点u0由无差拍单步FCS-MPC调节器产生.

3.1 稳态控制性能

电机在2 000 r/min带载稳态1 N·m条件下，对FCS-MPDTC和CCS-MPDTC进行性能对比，两种方法的权重系数P11=30、Q11=30.图5、图6分别是FCS-MPDTC和CCS-MPDTC仿真波形图，从上至下依次为电机机械转速、电磁转矩、定子磁链.两图对比可以看出FCS-MPDTC转速波动、转矩脉动、磁链脉动与CCS-MPDTC相比都较大.

图7和图8为上述两种方法的A相电流和电流THD仿真波形图，可以看出FCS-MPDTC定子电流中高频分量明显较多，同时电流THD较高为71.02%，CCS-MPDTC的电流THD为46.30%,CCS-MPDTC各项性能均优FCS-MPDTC.

本文CCS-MPDTC采用固定步长h=5，将迭代次数限制在10 000次.由图9可知大部分采样周期内迭代都到达了10 000次，没有到达极小点.由本节上述两种方法的稳态仿真波形图可以得出即使没有得到全局最优解，FCS-MPDTC的最终解仍然优于FCS-MPDTC的固定电压矢量.

3.2 动态控制性能

图10和图11分别给出了FCS-MPDTC和CCS-MPDTC电机在空载状态下由2 000 r/min下降到1 000 r/min时两种控制策略的性能表现，图中由上至下依次为电机机械转速和A相电流.由图8可以看出，两种方法均能很好的跟踪转速指令，速度响应时间基本相等，但CCS-MPDTC在转速突变时有更小的超调，且在定子电流更为平滑.

4 结论

本文针对表贴式永磁同步电机提出一种基于梯度下降法的CCS-MPDTC策略，本文证明了其价值函数在一定条件下是凸函数，可以使用标准的数值优化方法对电压矢量进行优化，优化起始电压矢量由FCS-MPDTC得出，最后通过SVM将优化电压矢量供给电机.通过对CCS-MPDTC和FCS-MPDTC两种方法进行了详细对比分析，结果表明所提出的CCS-MPDTC方法具有良好的动静态性能，并具有原理简单、算法执行迭代次数可限制的优点.