风险控制能力差异下的薪酬契约研究

倪宣明，赵慧敏，黄 嵩，钱 龙

(1. 北京大学软件与微电子学院，北京 100871； 2. 中山大学管理学院，广东 广州 510275;3.清华大学经济管理学院，北京 100084)

1 引言

代理人的道德风险(moral hazard)和逆向选择(adverse selection)问题一直是企业薪酬机制设计(mechanism design)中的核心问题，有时也与隐藏行动(hidden action)和隐藏信息(hidden information)等价。为了研究这一问题，Hurwicz[1]首先提出了机制设计的概念，Hurwicz[2]在优化问题中提出了激励相容(incentive compatible，IC)约束条件。Mirrlees[3-4]在构建道德风险模型时，借助分布函数参数化方法(parameterized distribution formulation)对激励相容约束进行数学处理，并指出企业高层经理的薪酬应与企业利润匹配。在此基础上，Holmstrom[5]用一阶条件来替代激励相容约束，极大地简化了问题的分析过程，被称为一阶条件方法(first order approach，FOA)，因此最优契约的条件也被称为Mirrlees-Holmstrom条件。Holmstrom[6]、Holmstrom和Milgrom[7]将以上模型推广到多任务情形，并探讨了充分统计量(sufficient statistics)问题。Rogerson[8]指出要想用一阶条件替代激励相容约束，必须增加分布函数凸性(convexity of the distribution function condition，CDFC)和单调似然比(monotone likelihood ratio condition，MLRC)两个假设，此时二阶条件自动满足。而Jewitt[9]指出该分析存在循环证明，需要对经理的效用函数施加更为严格的凹性要求，一阶条件方法才可能成立。Jewitt等[10]进一步分析了薪酬有界的情形。

显然，使用的一阶条件方法需要施加“强制凹性”假设，从而使必要条件与充分条件等价。这里，为避免凹性的假设，可以假设委托人风险中性、代理人存在具体效用函数，进而可以求出最优契约的显式解。但是，结合逆向选择与道德风险一起进行研究，激励相容约束条件的求解将更为复杂。实践中，不仅经理的努力水平很难被观测到，签约时的经理的能力同样难以观测，因此在股东和经理的博弈中，道德风险和逆向选择并存是更为普遍的现象。

既有研究引入隐藏行动的常见方法是将利润与经理的努力水平挂钩，努力水平越高，利润越高，但也会受到随机项的扰动影响。引入隐藏信息的方法主要包括两类，一类是将产出与经理的能力参数挂钩，经理能力水平越高，产出越高，另一类则是将成本与经理的能力参数挂钩，经理能力水平越高，成本越低。但是，既有的研究忽略了经理的风险控制能力。事实上，经理的风险控制能力，即对利润的波动的控制能力，同样是刻画经理能力的重要方面。经理更高的能力水平可以表现为既定的期望收益下，方差更小。这显然与常用的二阶随机占优(second-order stochastic dominance，SSD)有相似之处。

本文将风险控制能力视为经理的私有信息，认为能力越高的经理，其风险控制能力也越强。这里忽略了能力越高、产出越大的私有信息假设以简化分析，当然本文的分析框架也可以拓展至该情形。沿用文献中的普遍设定，本文假设股东风险中性和代理人风险规避，以利润的方差作为经理能力的衡量标准，构建了一个道德风险与逆向选择并存的企业薪酬的最优机制设计模型。假设经理人的绝对风险系数为常数(constant absolute risk aversion，CARA)的效用函数，本文得到显式最优解。

本文分别研究了两种不同能力的经理人在单一契约选择下和存在两种契约选择下的情形，发现在分离均衡下，股东的期望收益得以提高，但对低能力经理的激励下降，尽管对高能力经理的激励程度提高，但其效用却会下降。这是因为高能力经理所获得的补偿被低能力经理激励程度的下降所扭曲，这种补偿来自于经理风险控制能力的差异。股东还可以仅针对高能力经理设计单一契约，但当低能力经理所占的比例足够高时，针对性契约将失效，选择提供两种契约是股东的最优选择。对低能力经理而言，不管何种情形，均只能获得保留效用。

本文同时发现，股东提供两种契约还是针对性契约，存在以下两难困境。提供两种契约时，对高能力经理的激励补偿不仅与风险控制能力差异程度相关，也与对低能力经理的激励扭曲程度相关。因此，提供两种契约虽然可以获得低能力经理提供努力的收益，但却需要激励高能力经理而提供补偿。提供针对性契约可以获得高能力经理形成的剩余且无需补偿，但成本就是低能力经理所创造的利润。股东设计契约时需要在此两难困境下做出权衡。

相较于既有研究，本文从风险控制能力角度刻画了经理的能力差异，更加符合现实情况，在现有研究的基础上同时考虑了道德风险和逆向选择，通过引入异质经理人的概念，探究了在不同契约条件下的最优薪酬设计问题。本文求出的单一契约下的最优解和两种契约下分离均衡的显式解，以及针对高能力经理的单一契约解，可为私募基金等经理风控能力影响较大的行业提供薪酬决策上的重要参考。

2 隐藏信息与隐藏行动并存的最优契约

2.1 基本假设

在一个典型的公司制下，股东(委托人)负责公司的出资，并设计工资契约以聘请经理(代理人)。假设市场中存在高能力与低能力两种类型的经理，但无法被观测到，经理的能力信息属于其私有信息。若经理接受契约，将提供不可观测的努力水平，努力水平与风险共同决定利润。股东仅仅观测到利润，然后依据契约进行利润分配。显然，股东在设计最优契约时同时面临隐藏信息(能力高低)与隐藏行动(努力水平)问题。

沿用文献中的普遍做法，如Holmstrom[6]、Holmstrom与Milgrom[7]等，本文假设股东为风险中性，VNM(Von-Neumann-Morgenstern)效用函数为：v(x)=x。股东为经理设计的契约为线性工资契约，即：w(π)=F+δπ，这里F为固定工资，1>δ≥0为利润分成比例，π为利润。若δ>1，经理获得的分成工资超过利润，可通过借入外部资金充当利润进行套利，所有契约都将失效。若δ=1，经理获得所有利润，可看作是经理向股东租赁资本，道德风险和逆向选择问题将消失，因此本文仅考虑δ∈[0,1)的情形。

假设市场中的经理存在异质性，即存在高能力和低能力两种类型的经理，其VNM效用函数均为CARA型：u(x)=-exp(-ρx)，ρ>0为常数，代表绝对风险规避系数。同时假设市场上所有经理的货币化表示的成本函数相同：g(e)=0.5be2，b>0。经理的保留效用水平所对应的货币收益，即保留工资水平为A，A≥0。

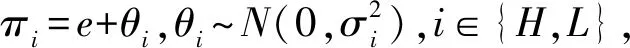
假设股东事先无法观测经理能力水平的高低，但知道市场中有比例或者概率为p∈(0,1)的L型经理和(1-p)的H型经理。

最后，忽略公司的运营成本、税收等因素。

2.2 基准模型：兼顾两种类型经理的单一契约

虽然股东知道市场上存在两种不同能力的经理人，但股东设计单一契约(F,δ)提供给市场上所有的经理。由于股东风险中性，其对应的期望效用为：

Ev=E(π-(F+δπ))=(1-δ)e-F

(1)

经理为CARA型效用函数，对应的期望效用为：

Eu=-exp{-ρ(F+δe-0.5be2

(2)

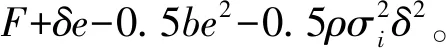
股东设计契约(F,δ)时，需要首先考虑经理的参与约束：

(3)

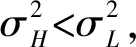
其次，还需考虑经理的激励相容约束，即经理选择努力水平使自身的期望效用或确定性等值最大化。

(4)

借助一阶方法(Firstorder approach,FOA)，可以将激励相容约束简化表示为：

(5)

股东设计契约对应的优化问题为：

(6)

求解(6)，可得最优契约及对应的最优努力水平：

(7)

进而可得股东、L型经理与H型经理的确定性等值分别为：

(CEP1,CEL1,CEH1)

(8)

从式(7)和式(8)可以得到以下结论：

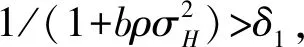
3 针对两种类型经理的分离均衡下的最优契约

3.1 分离均衡下的最优契约

从上节看出，若股东只设计针对所有经理的单一契约，将会造成对H型经理的激励不足。根据显示原理，如果设计两种契约(FH,δH)和(FL,δL)，以实现H型经理选择契约(FH,δH)、L型经理选择契约(FL,δL)的目标，即可实现分离均衡。但股东在设计契约时，需要考虑两类经理对自身类型进行伪装的可能性。

由于经理人同时存在隐藏信息(H和L)和隐藏行动(努力水平)，本文需首先考虑隐藏行动的激励相容约束。如果任意类型的经理选择接受契约(Fi,δi)，i∈{H,L}，则其选择努力水平所对应的激励相容约束为：

i,j∈{H,L}

(9)

因此，对任意类型的经理而言，一旦接受契约(Fi,δi)，其对应的激励相容约束可以简化为：e=δi/b。任意类型的经理，其最优努力水平由其所选择的契约中的利润分成比例所决定。

股东设计两种契约的目标是要实现以下分离均衡：L型经理选择契约(FL,δL)，H型经理选择契约(FH,δH)。将简化的隐藏行动的激励相容约束代入，股东设计最优契约对应的优化问题为：

(10)

其中，IPL和ICL为L型经理的参与约束和隐藏信息的激励相容约束；IPH与ICH为H型经理的参与约束和隐藏信息的激励相容约束。

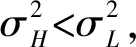
(11)

因此，约束IPH自动满足。令λ、φL和φH分别为约束IPL、ICL和ICH的Kuhn-Tucker乘子，(λ,φL,φH)≥0，对应的Kuhn-Tucker条件为：

-p+λ+φL-φH=0

(12)

-(1-p)-φL+φH=0

(13)

(14)

(15)

加上对应约束的互补松弛条件共同构成优化问题(10)的解。下面通过命题1-3来求解最优契约。

命题1λ>0，φH>0。

由式(12)和式(13)知，λ=1>0及φH=(1-p)+φL>0。λ>0和φH>0表明L型经理的参与约束IPL和H型经理的激励相容约束ICH束紧。

命题2δH>δL>0。

证明首先证明δL>0。若δL=0，代入式(14)可得p/b>0，这与式(14)矛盾。同理，由式(15)可得δH>0。δL>0与δH>0表明式(14)与式(15)等号成立。

将1+φL=p+φH代入式(14)和式(15)整理可得：

(16)

(17)

因此：

(18)

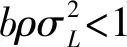
综上，δH>δL>0，证毕。

命题3φL=0。

证明用反证法。不妨假设φL>0，则约束ICL束紧，联立ICH与ICL，整理可得：

(19)

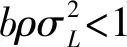
结合命题1、命题2、命题3可知，约束IPL和ICH束紧，而约束IPH和ICL中的不等式自动满足。要实现分离均衡，L型经理仅需满足参与约束，但需要对H型经理进行激励补偿。在此基础上，对应的最优契约(FL2,δL2)及(FH2,δH2)为：

(20)

对应的最优努力水平为：

(21)

股东、L型经理与H型经理的确定性等值分别为：

(CEP2,CEL2,CEH2)

(22)

3.2 对比单一最优契约模型的讨论

兼顾两种类型的分离均衡下的最优契约{(FL2,δL2),(FH2,δH2)}与单一最优契约(F1,δ1)相比，具有以下几个特征。

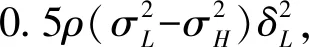
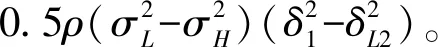
第四，在契约{(FL2,δL2),(FH2,δH2)}下，相比契约(F1,δ1)而言，股东的收益会上升，这由下式可以直观看出：

(23)

单一契约忽略了对H型经理的激励，此时进行伪装可以获得充分的额外收益。为了激励H型经理提高努力水平以创造更高的利润，通过设计契约{(FL,δL),(FH,δH)}以实现分离均衡，虽然L型经理的激励受到一定程度的扭曲，但是H型经理会提供更高的努力水平，但相比混合时会损失一定的效用，这部分损失被转给股东，最终会使得股东的期望收益上升。

第五，在契约{(FL2,δL2),(FH2,δH2)}或单一契约(F1,δ1)，L型经理均只能获得保留效用。无论是实现分离均衡的双契约{(FL,δL),(FH,δH)}还是单契约(F,δ)，L型经理的参与约束都处于束紧形式，均为保留收益A。而在双契约{(FL,δL),(FH,δH)}下，在优化问题(10)中，L型经理的激励相容约束ICL所对应的乘子在最优解中φL=0，分离均衡下的契约仅需要考虑对H型经理的激励。因此，L型经理在两种情形下均只能获得保留效用。

4 针对高能力经理的单一契约

4.1 针对高能力经理的最优契约

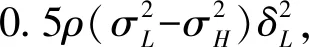
结合前面分析可知，股东此时的优化问题为：

(24)

求解优化问题(24)，可得最优契约及对应的最优努力水平：

(25)

进而可得股东、L型经理和H型经理的确定性等值分别为：

(CEP3,CEL3,CEH3)

(26)

这里，L型经理尽管选择不接受契约，但还是能获得保留收益A。

4.2 与基准模型及分离均衡模型的比较

股东仅针对H型经理而设计的单一契约，相比针对两类经理的基准模型而言，尽管后者也是单一契约，但由于兼顾L型经理，激励程度不足；相比分离均衡模型而言，此时最优契约尽管不需要对H型经理进行补偿，但损失了L型经理努力所能创造的收益。具体体现在以下几个方面。

第一，在三个模型中，L型经理均只能获得保留收益。在单一契约(F3,δ3)下，L型经理会拒绝该契约而获得保留收益A。若选择接受该契约，收益反而会低于A，即该契约仅仅针对H型经理。

第二，H型经理的激励不受到扭曲。与契约{(FL2,δL2),(FH2,δH2)}相比，显然可知δ3=δH2且e3=eH2。因为契约(F3,δ3)仅针对H型经理，此时对H型经理的激励与分离均衡下的激励相同，都高于基准模型中对H型经理的激励程度。

第三，H型经理此时仅能获得保留收益。由于股东设计的契约(F3,δ3)仅针对H型经理，此时不需要考虑H型经理伪装成L型经理的可能性，后者不会选择接受该契约，因此也不需要给予H型经理真实显示其类型而进行的补偿。单一契约(F3,δ3)下，H型经理显然只能获得保留收益A。

第四，股东的期望收益与前两种契约相比，取决于外生参数之间的关系。首先比较与分离均衡契约{(FL2,δL2),(FH2,δH2)}下的期望收益。由下式可知：

CEP2>CEP3

(27)

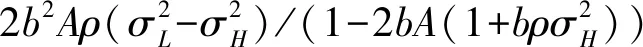
同理分析可知，对单一契约而言：

CEP1>CEP3

(28)

当L型经理的比例p足够高时，对股东而言，忽略L型经理、只针对H型经理的单一契约(F3,δ3)并非明智的选择。明显得CEP2>CEP1，因此，兼顾两类经理的分离契约{(FL2,δL2),(FH2,δH2)}才是股东的最优选择。

5 数值模拟

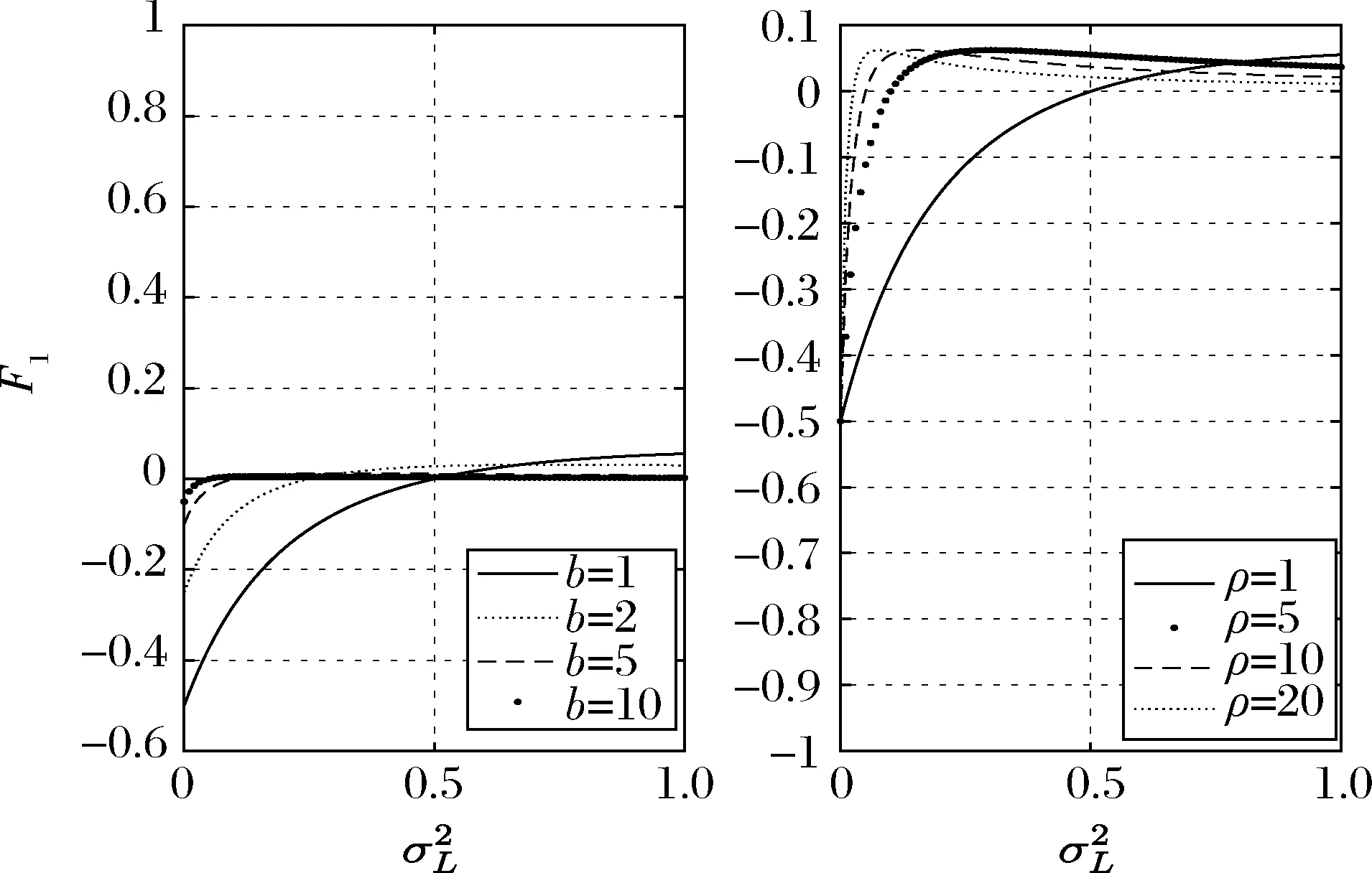
图1 兼顾两类经理的单一契约中不同参数对固定工资的影响

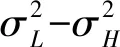
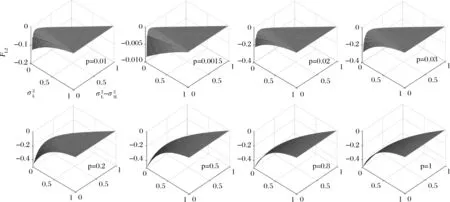
图2 分离均衡下不同概率对L型经理固定工资的影响

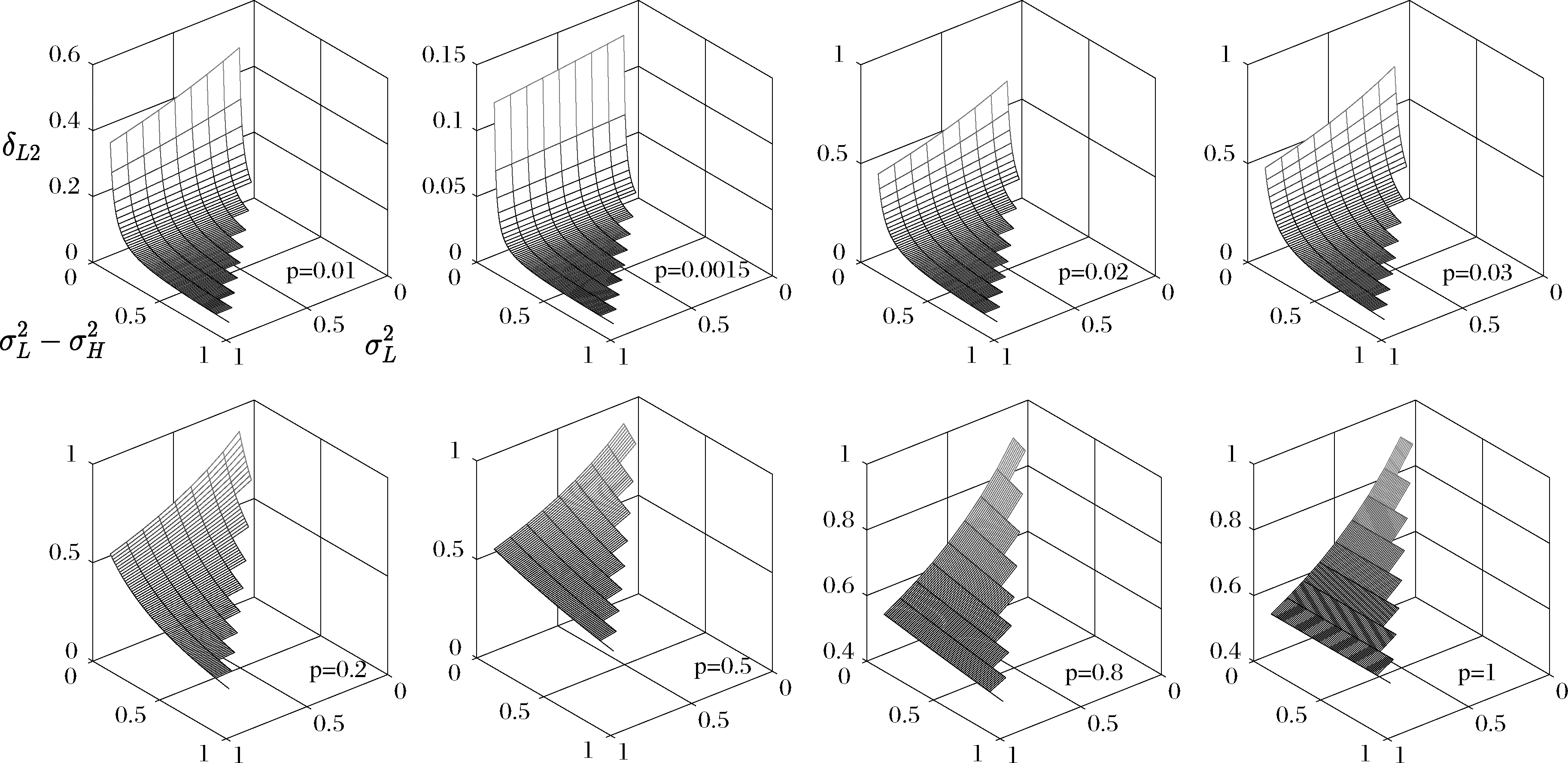
图3 分离均衡下不同概率对L型经理利润分成的变化

图4 分离均衡下不同概率对H型经理固定工资的变化

针对高能力经理单一契约(F3,δ3)的模拟与基准模型相同。同样令A=0，ρ=1，b取四种不同值以及令b=1，ρ取四种不同值。若只针对H型经理设计契约，那么如同基准模型中的情况，经理的能力越强，获得的固定工资越低，利润分成比例越高。

图5 经理能力差距对股东契约选择的影响

6 结语

本文假设市场中存在异质经理人，并以他们对利润的风险控制水平的不同来代表经理的能力差异，并且同时考虑道德风险和逆向选择下的最优薪酬设计问题。假设经理的效用为CARA效用函数，本文求出了单一契约的最优解和两种契约下的分离均衡的显式解。

本文发现分离均衡下的最优契约与针对两类经理的单一契约相比，股东的期望收益得以提高。对低能力经理而言，激励下降。而对高能力经理的激励程度尽管提高了，利润分成比例也变大，但其期望效用或确定性等值反而会下降，这是因为高能力经理因能力差异所获得的补偿由于契约对低能力经理的激励程度下降而被扭曲。在单一契约下，股东设计契约没有考虑能力差异，高能力经理会选择伪装成低能力经理以得到充分的伪装收益。在分离均衡下，高能力经理不可能选择伪装，只能选择激励高的合约，其收益也会因为低能力经理的激励程度下降而下降。

另外，本文认为股东在设计契约时，还存在仅针对高能力经理提供单一契约的情形。具体选择分离均衡契约还是针对高能力经理的单一契约，主要取决于低能力经理所占的比例。只要低能力经理的比例足够高，忽略该类经理所形成的收益损失也将会足够高，这样对股东而言，兼顾两类经理的分离均衡契约将是股东的最优选择。