引入初始因子时滴定方程的理论构建及曲线模拟
2021-01-04武伟国
武伟国
引入初始因子时滴定方程的理论构建及曲线模拟
武伟国
(甘肃省农业科学院 经济作物与啤酒原料研究所,甘肃 兰州 730070)
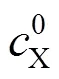
滴定方程;滴定曲线;初始因子;滴定分数
1 理论假设
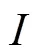
2 滴定方程的求解
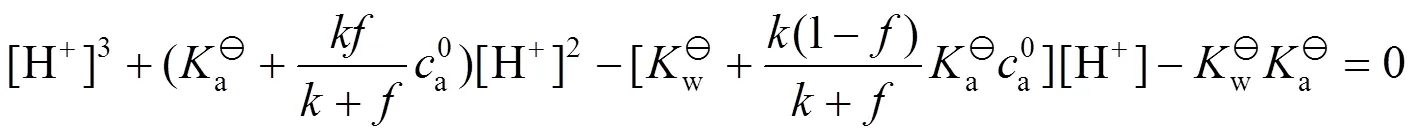
根据方程(1)求解得
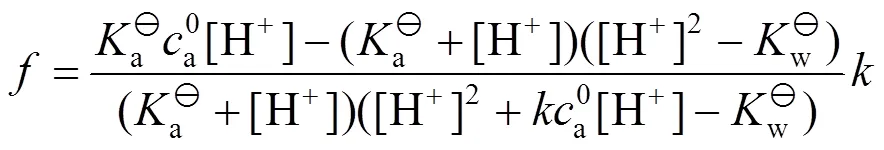
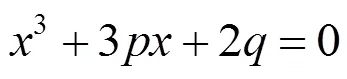
,的表达式分别为
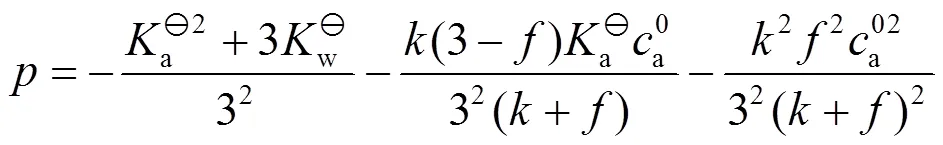
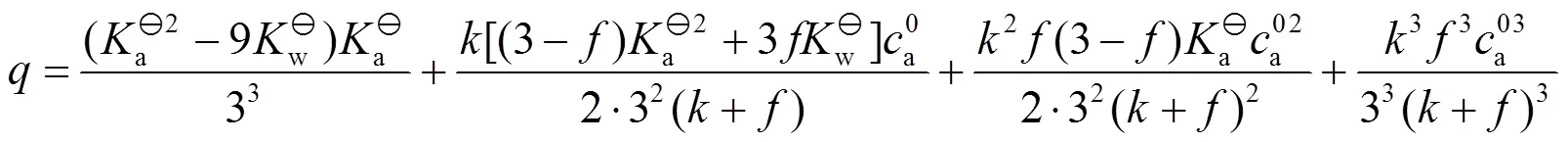
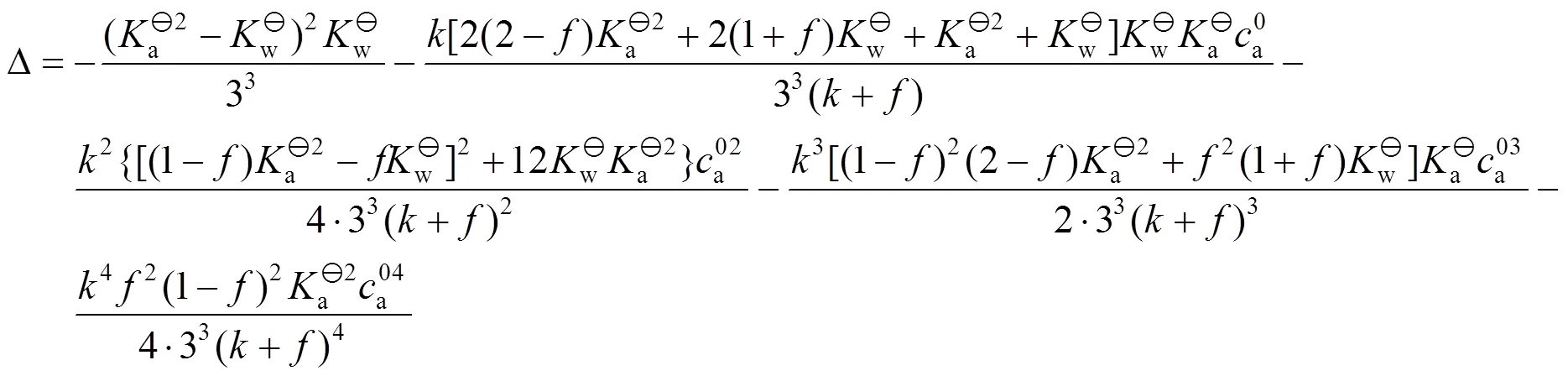
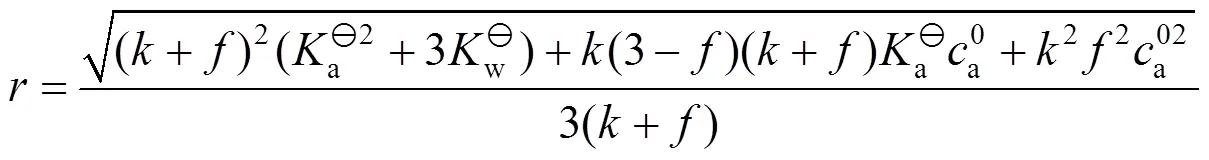

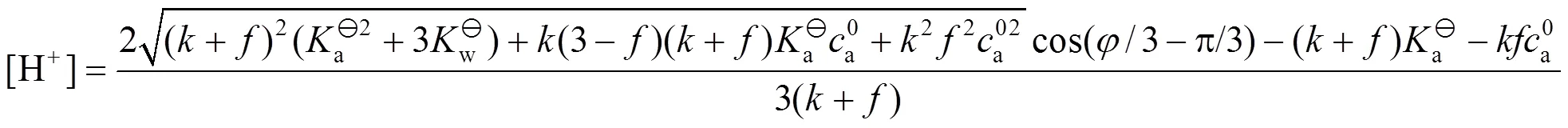
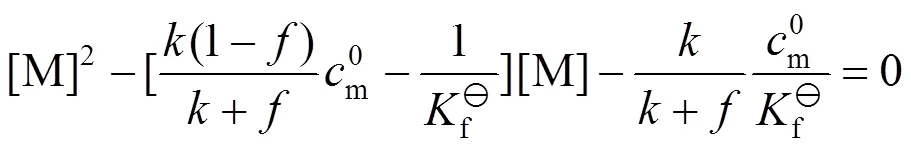
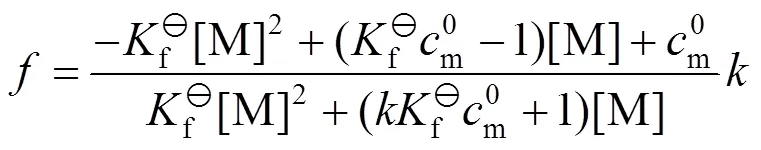
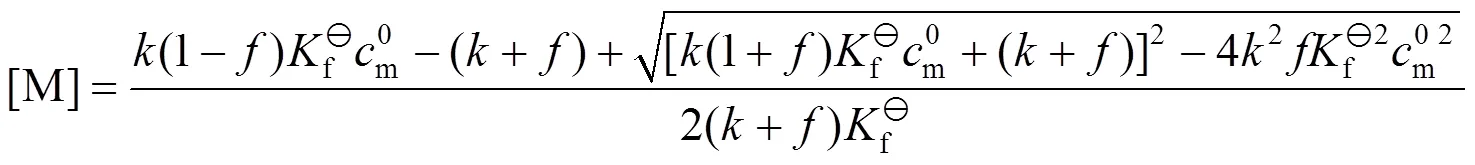


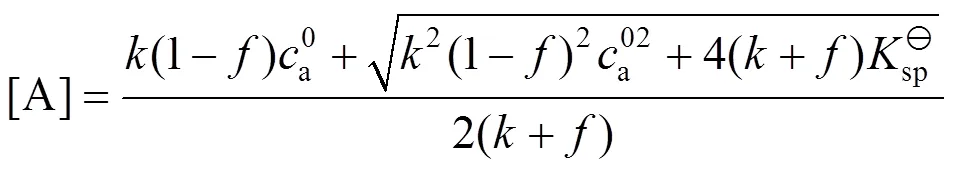
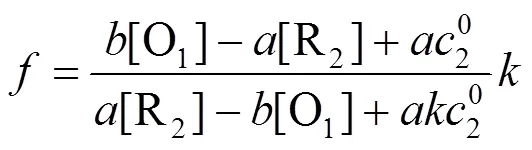
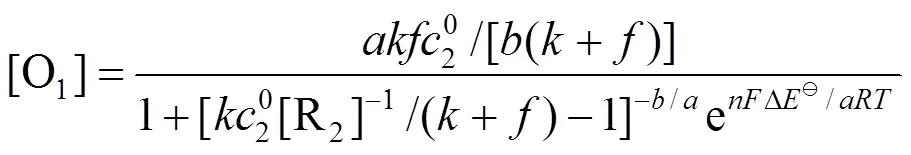
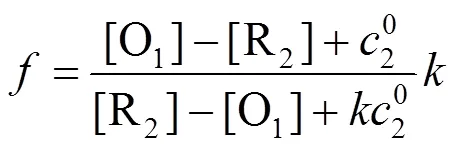
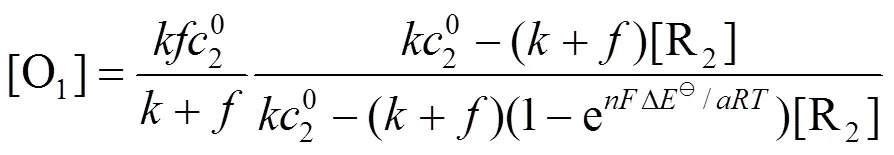
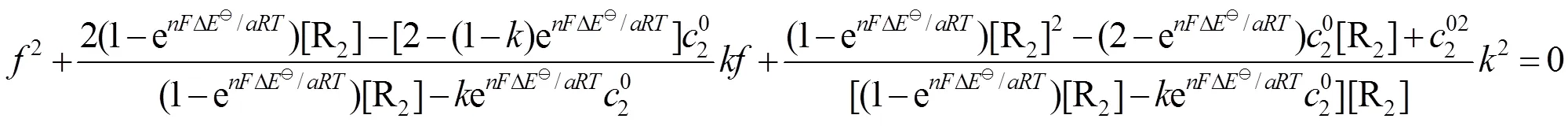
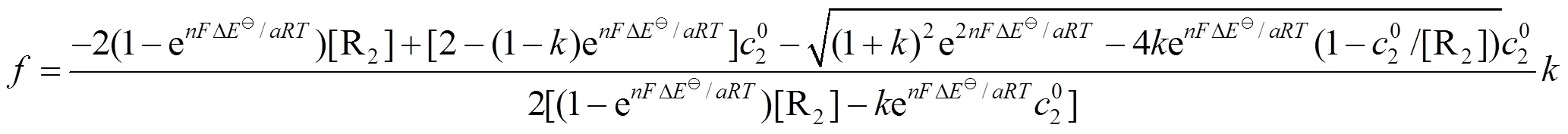
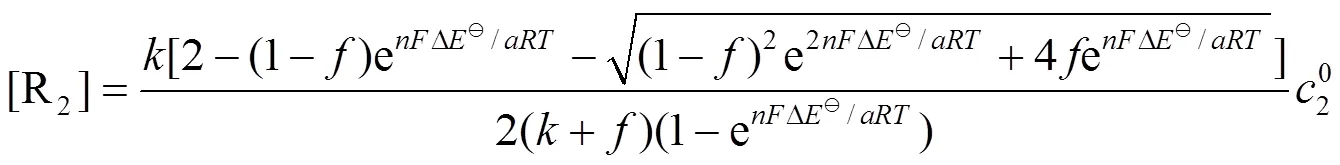
3 滴定曲线的绘制
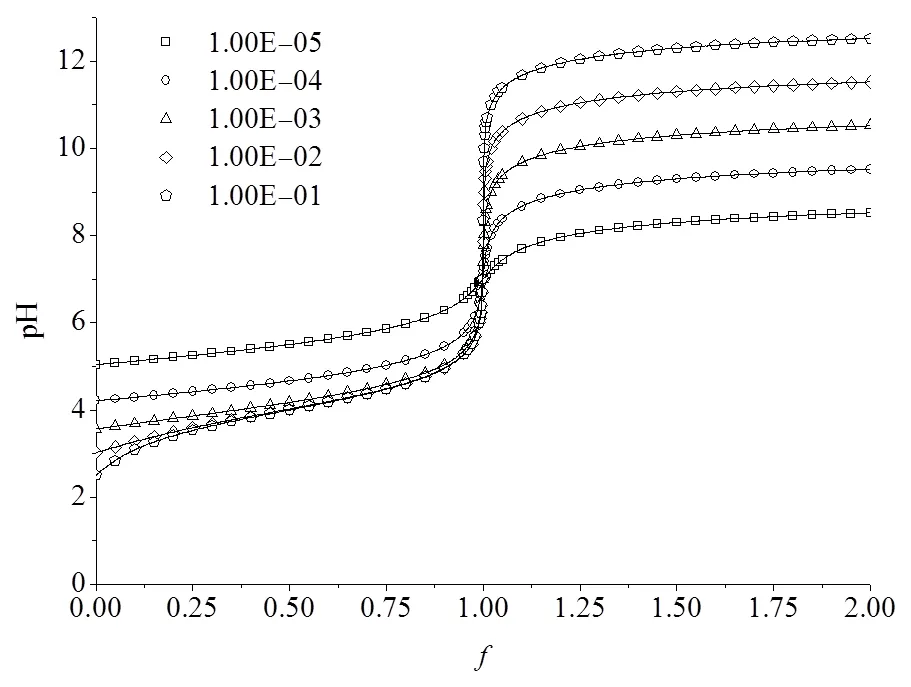
图1 ,k恒定而不同时的酸碱滴定曲线
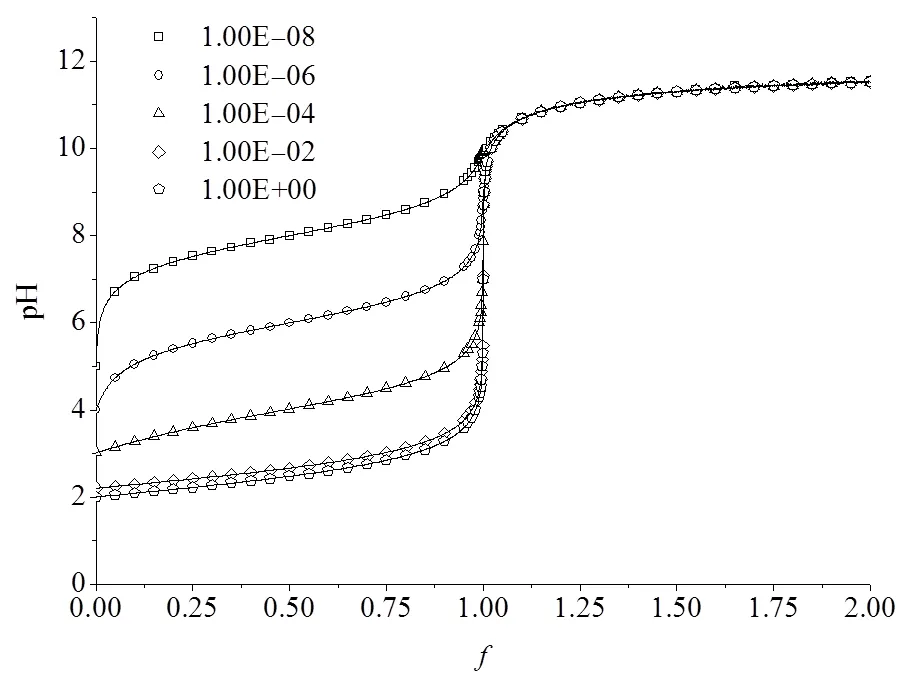
图2 ,k恒定而不同时的酸碱滴定曲线
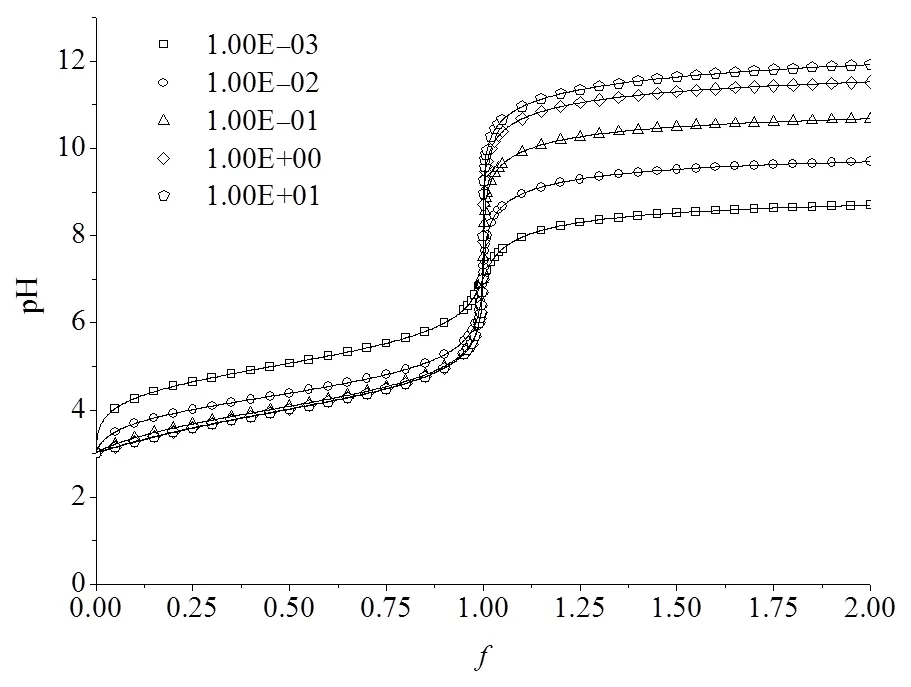
图3 ,恒定而k不同时的酸碱滴定曲线
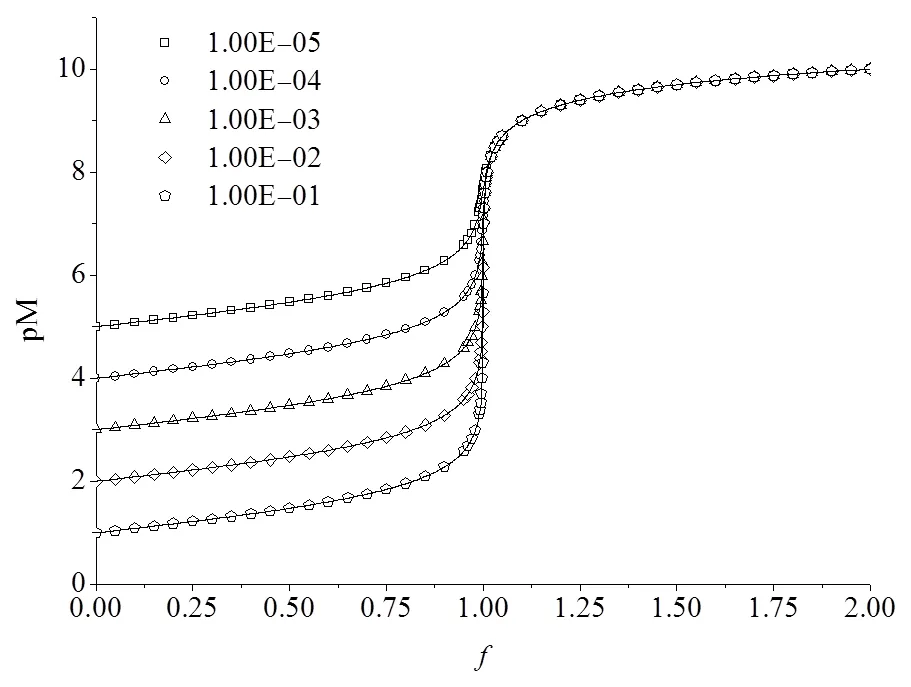
图4 ,k恒定而不同时的配位(络合)滴定曲线
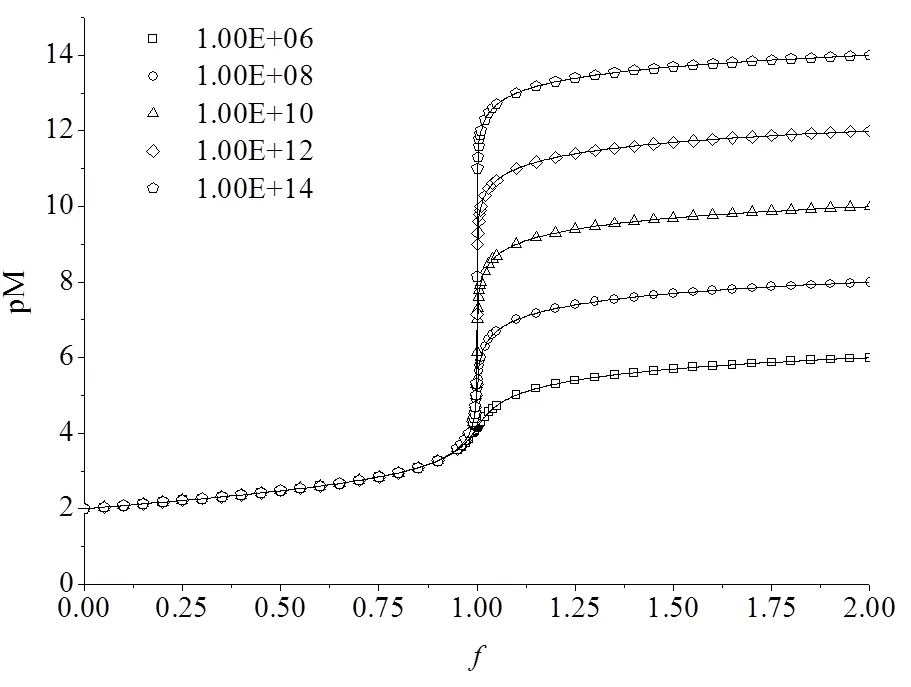
图5 ,k恒定而不同时的配位(络合)滴定曲线
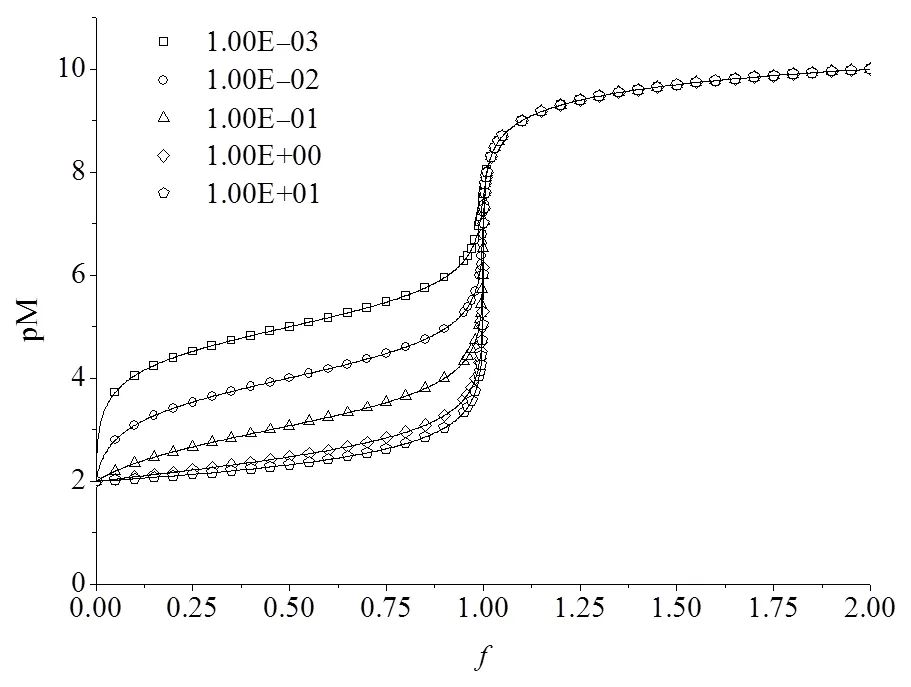
图6 ,恒定而k不同时的配位(络合)滴定曲线
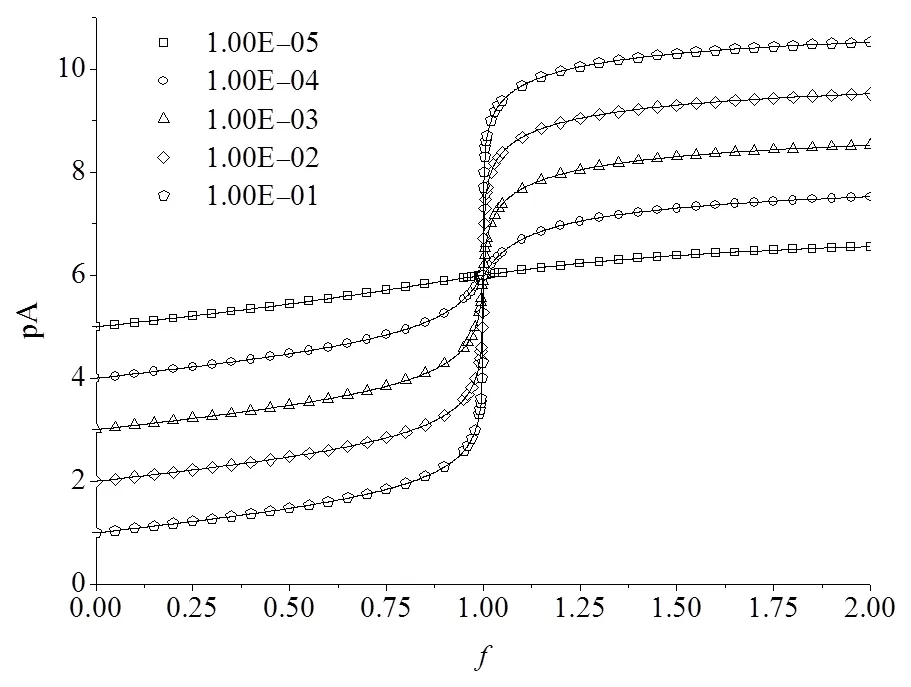
图7 ,k恒定而不同时的沉淀溶解滴定曲线

图8 ,k恒定而不同时的沉淀溶解滴定曲线
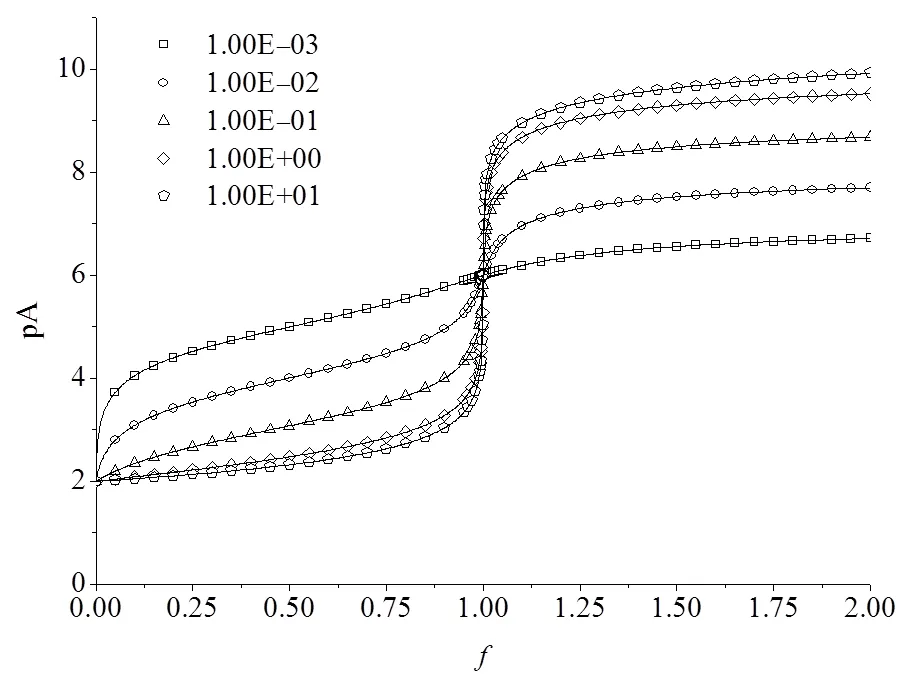
图9 ,恒定而k不同时的沉淀溶解滴定曲线
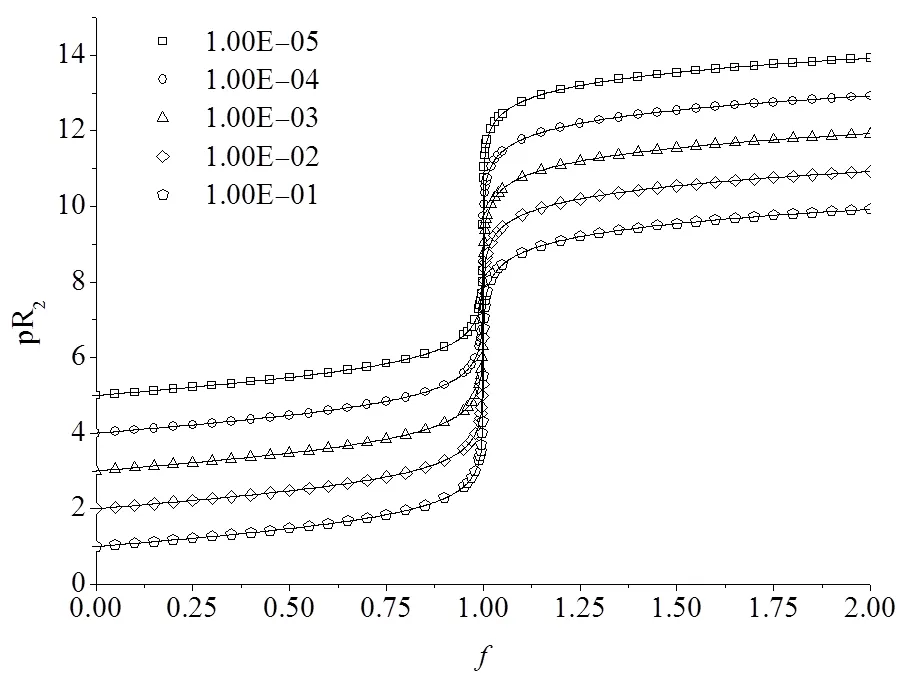
图10 ∆Ey,k恒定而不同时的氧化还原滴定曲线
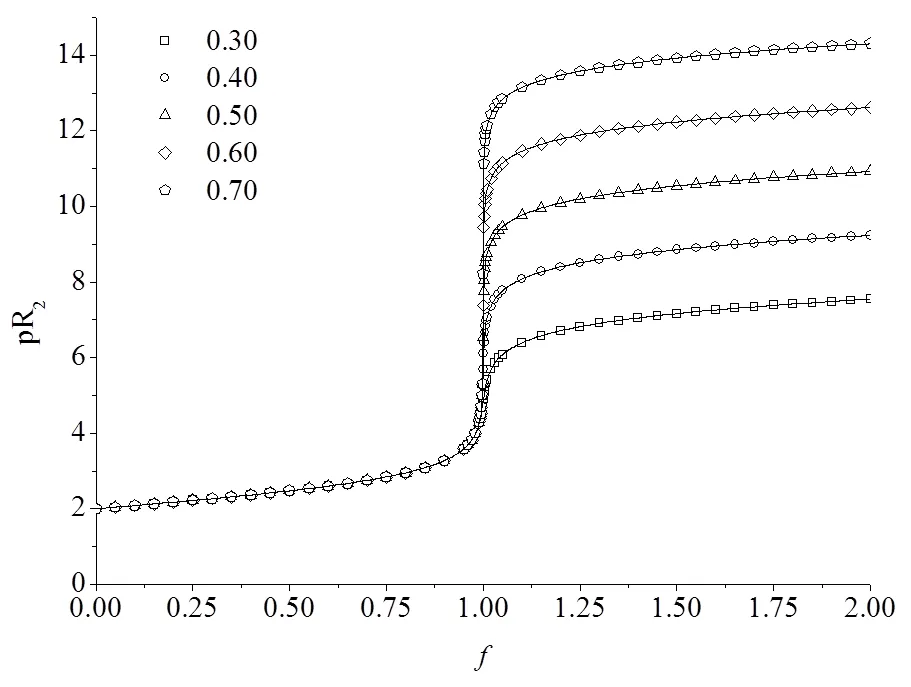
图11 ,k恒定而∆Ey不同时的氧化还原滴定曲线
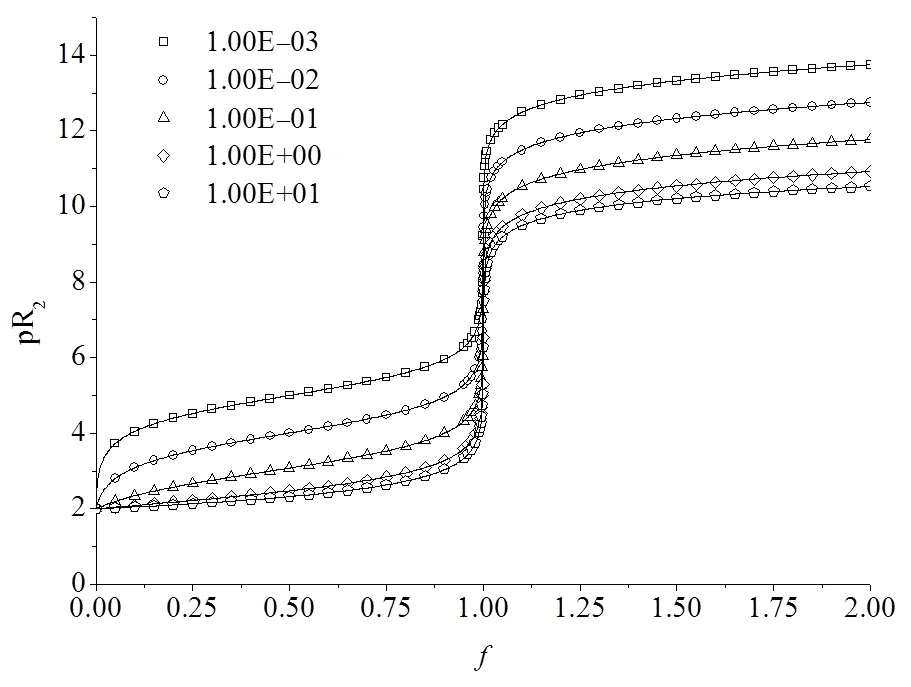
图12 ∆Ey,恒定而k不同时的氧化还原滴定曲线
4 结论
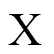
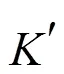
[1] 武汉大学.分析化学[M].4版.北京:高等教育出版社,2000:204-208
[2] Ringbom A.分析化学中的络合作用[M].戴明,译.北京:高等教育出版社,1987:76-79
[3] 孟凡昌,蒋勉.分析化学中的离子平衡[M].北京:科学出版社,1999:98-112
[4] 武伟国.等浓度条件下滴定方程的理论构建及曲线模拟[J].高师理科学刊,2015,35(2):48-51
[5] 邢富冲.一元三次方程求解新探[J].中央民族大学学报:自然科学版,2003,12(3):207-218
[6] 大连理工大学.无机化学[M].4版.北京:高等教育出版社,2001:192-193
[7] 武伟国.涉及多元酸碱和不对称氧化还原电对的滴定分析[J].高师理科学刊,2015,35(3):41-46
Theory construction and curve simulation of titration equation when initial factor incorporated
WU Weiguo
(Institute of Economic Crops and Beer Materials,Gansu Academy of Agricultural Sciences,Lanzhou 730070,China)
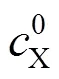
titration equation;titration curve;initial factor;titration index
O655.2
A
10.3969/j.issn.1007-9831.2020.11.012
1007-9831(2020)11-0054-07
2020-06-08
武伟国(1985-),男,甘肃会宁人,助理研究员,硕士,从事生物化学与分子生物学研究.E-mail:physchem@163.com
