基于非规则网格模型的全球潮流能评估

陈禹庚，鲍献文*，周玲玲，姚志刚

(1.中国海洋大学 海洋与大气学院，山东 青岛 266100)

1 引言

传统化石能源属于不可再生能源，化石能源的大量消耗已带来一系列的环境问题，导致全球气候变暖、海平面上升等严重的后果。减少化石能源消耗，寻找绿色可替代能源，构建全球新能源体系已迫在眉睫。海洋面积占地球总面积的70.8%，高达3.61×108km2，其中蕴藏着巨大的海洋可再生能源。海洋能具有可预测、可再生、可持续利用等特点，是有利于人类社会和谐发展的重要绿色能源之一。潮流能作为海洋能的重要组成部分，其开发的基本原理是将海水的动能转化为机械能，进而通过机械能发电，开发过程不排放任何有害污染物，是一种适于直接开发的可再生环境友好型能源。然而相比于潮汐能，潮流能的开发较晚，直到1973 年美国科学家莫顿提出科里奥利系统，才标志着潮流能的开发取得了实质进展。联合国环境署最新发布的《Renewables 2018 Global Status Report》[1]（《2018 年全球可再生能源现状报告》）指出，在截至2018 年年底总量约为529 MW 的海洋能发电中，潮汐发电占了90%。进入21 世纪，潮流能开发技术发展迅速。2008 年5 月，英国MCT 公司建成1.2 MW的“SeaGen”海洋发电机，是世界第一台兆瓦级别的潮流能发电装置[2]，而后，Altantis Resources 公司以及挪威的Hammerfest Strøm 公司也先后开发出了兆瓦级潮流能发电装置。同时，已经有公司开始了潮流能发电厂的建设，如Marrine Current Turbine 公司计划建设8 MW 和10 MW 的潮流能发电场；韩国的全罗南道莞岛也正在建设两座大型潮流能发电场。MeyGen 公司计划在苏格兰安装将近400 个潮流能发电机组，总装机功率达398 MW。2015 年7 月，英国政府批准了耗资10 亿英镑的潮汐潟湖项目[3]。2016 年8 月，世界首台3.4 MW 的LHD 林东模块化大型海洋潮流能首套1 MW的发电机组正式并入中国国家电网，首年年发电量达到了181 300 kW·h[4]。自此，我国海洋能利用技术取得了重大突破，成为继英、美之后，全球第三个全面掌握潮流能发电并网技术的国家，标志着我国在海洋潮流能利用领域跨入领先行列。然而，迄今国际上尚未系统地绘制出全球潮流能资源分布图，本文基于全球纯动力潮汐非规则网格模型的潮汐模拟结果，计算出全球近岸潮流能密度，较系统评估了全球范围内海洋潮流能的分布，为潮汐和潮流能合理开发和利用提供科学支撑。

全球潮汐的模拟开始于20 世纪60 年代[5]，基于当时十分粗糙的网格和并不精确的水深资料，所得到的全球潮汐结果与事实并不相符，不同学者得到的结果之间也相差很大。20 世纪80 年代，Schwiderski[6]开始将全球潮汐模型的模拟结果与验潮站实测资料相结合，一定程度上提高了模型的准确性。21 世纪以后，长时间且丰富的全球卫星高度计资料被应用到了全球潮汐的数值模拟中，建立了精确度很高的全球潮汐同化模型。目前，全球潮汐模型分为3 类：（1）全球潮汐经验模型，对验潮站数据和卫星高度计数据进行主客观分析，得到潮汐调和常数等信息，获得全球潮汐分布，例如CR91、GOT00、CSR4.0 等；（2）纯动力全球潮汐模型；（3）全球潮汐同化模型，通过同化方法来优化潮汐的模拟结果，例如TPXO、FES2004、NAO99 等。纯动力全球潮汐模型独立于任何卫星及实测的外部资料，基于理论方程还原潮汐。近几十年来，随着人类对海洋认识的不断深入，纯动力全球潮汐模型也取得了长足的发展，模拟精度显著提高。目前纯动力全球潮汐模型模拟的准确性主要与以下几个方面有关：空间分辨率、地形数据以及对潮汐耗散的理解[7]。

现有观测资料表明，强潮流一般分布在近海陆架、岛屿通道等局部海域，受地形、岸线岬角以及岛屿等多种因素影响。因此，采用非规则三角网格技术，实现对岛链、陆架和群岛海域局部加密模拟全球潮汐潮流，才有可能再现强流区的潮流特征。非规则三角网格是可任意局部灵活加密的无结构网格，可以更好地拟合特征复杂的不规则海岸线和地形，也可自行对大洋中脊等深海粗糙复杂地形进行加密。更为重要的是，目前的纯动力全球潮汐模型普遍使用的是规则网格，由于规则网格在处理地球极点的弊端，无法使规则网格延伸到北极点（南极点为南极大陆），因为规则网格在接近北极点的过程中会使网格间距无限变小，使其数值计算不收敛。因此，对于采用规则网格的纯动力全球潮汐模型必然要在高纬度地区取开边界，在开边界上靠卫星数据或其他模型数据驱动，无法做到完全独立于外部数据，而非规则三角网格则克服了这一缺陷，可使非规则三角网格覆盖全球，实现模型完全由天体引潮力驱动，独立于外部数据。同时潮流模拟的准确性很大程度上取决于近岸区域的地形、水深数据的准确性，而对于近岸地区的细化加密正是非规则三角网格的优势所在。本模型所采用的非规则三角网格在对分辨率要求不高的深海大洋区域所采用的网格较粗，在不影响计算结果的情况下节约了计算时间，保证了计算效率。

2 数值模型构建

本文基于网格有限体积海洋模式（Finite-Volume Community Ocean Model，FVCOM），自行添加了内潮耗散项及自吸引-负荷潮模块，用天体引潮力驱动全球正压潮汐模型。FVCOM 是美国麻省理工大学海洋科学技术学院和美国伍兹霍尔海洋研究所联合开发的海洋模型，采用非规则三角网格和有限体积的方法。动量方程如下[8]：

式中，u为水平流速；U为水平输运速度，为水平速度u与水深H的乘积；f为科氏力参数；g为重力加速度，本文取9.81 m/s2；H为水体总体深度；ζ为瞬时潮位；α为体潮Love 数（各分潮Love 数在2.4 节中给出)，体潮是指地球本身在天体引潮力作用下发生形变形成的潮汐；ζEQ为平衡潮潮位（将在2.4 节中提到）；ζSAL为自吸引-负荷潮位（将在2.2 节中提到）；ζMEM为前后迭代的记忆潮位（将在2.3 节中提到）；aH为水平湍流涡黏度系数，本文取103m2/s；Cd为底摩擦系数，本文取0.002 5；为内潮耗散项，N为底层浮力频率，h为海底粗糙度，k为调节参数。

2.1 内潮耗散项的计算

基于对TOPEX/Poseidon 卫星数据的反演分析提出约有1 TW 的能量耗散在深海[9-10]，并且深海耗散主要发生在大洋中脊等地形粗糙地带。传统的底摩擦耗散项表示为

式中，海水平均密度ρ0取值1 023 kg/m3，底摩擦系数Cd取值0.002 5。然而在深海，海底流速约为2 cm/s，此时的深海耗散能量量级仅为0.02 mW/m2，完全不足以平衡实际的深海能量耗散。因此，Jayne 和Laurent[11]提出了一个内潮拖曳参数化方案，得到一个水平变化的线性拖曳系数，N为底层浮力频率，h为海底粗糙度，k为调节参数，通过调节k来获得最优的模拟结果。N的计算公式为

式中，ρ为海水密度，单位kg/m3，z为水深，单位m。

本文所用的浮力频率由WOA13 数据计算得到，随后插值到模型计算网格。本文所用的计算海底粗糙度的计算方法为：计算每个网格点（1/4）°范围内的地形数据（GEBCO）的标准差记为该点的粗糙度h。对于调节参数k，经过大量模型实验测试，将其在模型中设为1.83·2π/104。表1 给出了加入内潮耗散项前后M2分潮的耗散变化，加入内潮耗散项后深海耗散明显增加，从0.02 TW 上升至0.95 TW，占比达到了36.68%，其结果与Egbert 和Ray[9]研究指出的深海耗散占总耗散约1/3 的结果较为接近，不同之处在于Egbert 和Ray[9]得到的总耗散结果在2.45 TW 左右，而本文得到的结果在2.6 TW 左右，造成差异的原因主要是计算方法的差别：Egbert 和Ray[9]是通过对卫星高度计数据进行经验反演得到底部耗散，而本文是通过模式输出的底应力乘以速度后进行全球积分得到的底部耗散，同时由于其规则网格的步长计算限制，Egbert和Ray[9]无法统计靠近极点的高纬海域，而本文所采用的非规则网格则计算了全球海域，耗散结果必然会增加，且卫星高度计数据相对于模式输出的数据分辨率更粗。为了进一步对比耗散的分布，将本文模式得到的全球耗散分布与Jayne 和St Laurent[11]给出的结果进行对比，图1 为Jayne 和St Laurent[11]给出的潮汐耗散分布，图2 及图3 分别为本模式加入内潮耗散项前后的耗散分布。由图1 至图3 可见，本文模式得到的耗散分布与Jayne 和St Laurent[11]给出较为一致，加入内潮黏性项后深海耗散增加的海域主要集中在大洋中脊，西太平洋、大西洋以及西印度洋都是深海耗散较大的海域。

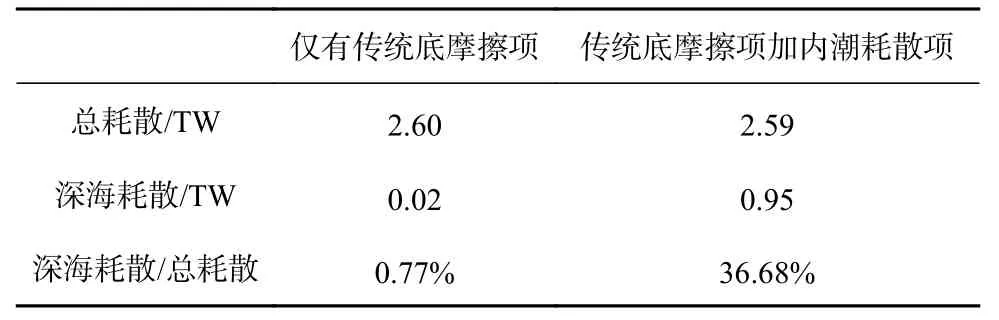
表1 加入内潮耗散项前后的 M2分潮耗散Table 1 Dissipation of M2 before and after adding parameterization of internal tidal dissipation

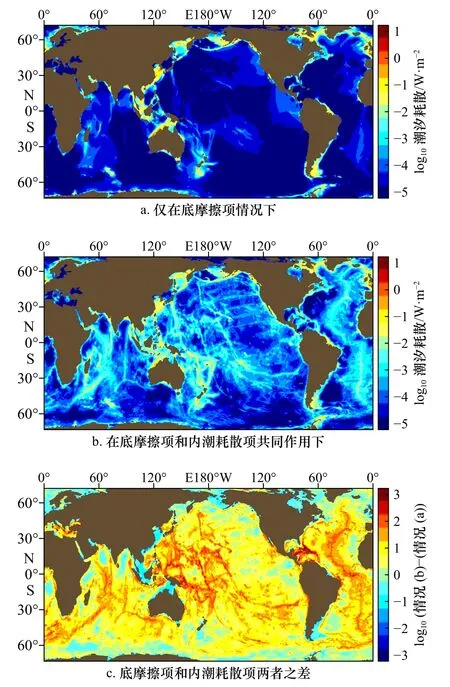
图1 潮汐耗散分布（据文献[11]）Fig.1 Distribution of tidal dissipation (based on reference [11])

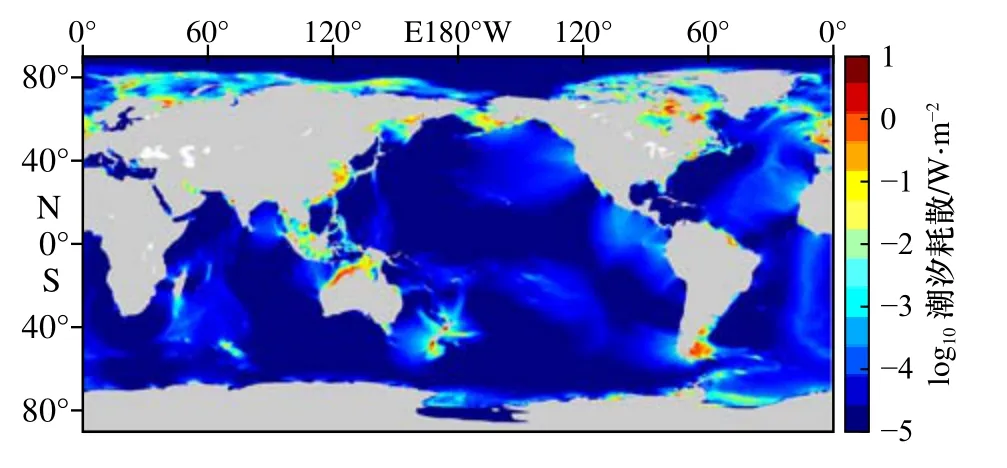
图2 本文模式在仅有底摩擦项情况下的潮汐耗散分布Fig.2 Tidal dissipation with bottom drag only of the model in this paper

2.2 自吸引-负荷潮的理论计算

自吸引-负荷潮是由潮汐对固体地球表面的负荷作用而产生的，主要由海水自吸引作用和固体地球表面的形变两部分组成。目前最简单的自吸引-负荷潮计算方法为线性化近似，即

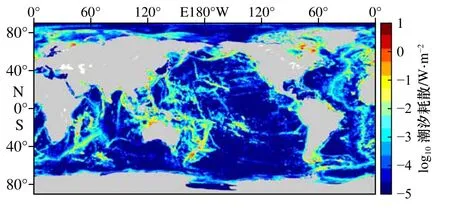
图3 本文模式在底摩擦项和内潮耗散项共同作用下的潮汐耗散分布Fig.3 Tidal dissipation with bottom drag and internal-tide drag of the model in this paper

式中，ζSAL为自吸引-负荷潮潮高；β是一个常数，通常取值在0.085～0.100 之间，然而Ray[12]指出，这种近似十分粗略，不可能找到一个适用于全球海洋的常数β。显然这种近似也忽略了自吸引-负荷潮独立于当地潮位的相位变化。

本文采用Farrell[13]提出的Green 函数方法计算自吸引-负荷潮，根据该方法任何地点的自吸引-负荷潮潮高可由下式得到:

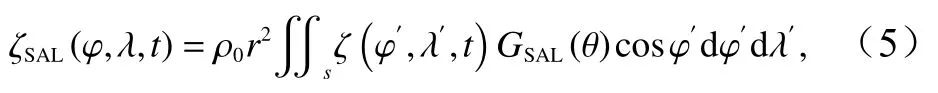
式中，(φ,λ)为计算点纬度和经度；φ′,λ′为自吸引-负荷点的纬度和经度；ρ0为海水密度（；r为）地球半径；积分对全球海洋s进行；θ为(φ,λ)和φ′,λ′之间的角距离，计算公式为

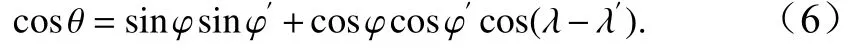
GSAL为对应的Green 函数，由下式得到：

式中，Me为地球质量；Pn为n阶Legendre 多项式。组合自吸引-负荷Love 数取自文献[3] 中表A2 所给的结果。

根据本文模型的最终潮汐结果，运用上述自吸引-负荷潮计算公式，计算了现在全球的自吸引-负荷潮分布，并绘制了 M2分潮的自吸引-负荷潮同潮图与Ray[12]给出的 M2分潮自吸引-负荷潮同潮图进行对比。图4 与图5 分别为根据本文模式最终结果计算得到的 M2分潮自吸-负荷潮的等振幅线和同潮时线；图6 和图7 分别为Ray[12]给出的 M2分潮自吸-负荷潮的等振幅线和同潮时线。由图4 至图7 可见，本文模式计算所得到的自吸引-负荷潮的同潮图与Ray[12]给出的基本一致，说明了本文在计算自吸引-负荷潮的过程中所用的方法与参数的正确性以及结果的准确性。

2.3 自吸引-负荷潮的数值方法

本文通过带记忆效应的迭代方法[14-15]将自吸引-负荷潮严格化处理的结果加入到模型中。首先通过一次自吸引-负荷潮的线性化近似ζSAL=βζ （β取0.093）运行一次模型；模型运行完毕后，将得到的潮位结果通过ζSAL的计算公式得到严格计算处理的自吸引-负荷潮计算结果。而后对得到的自吸引-负荷潮潮位进行调和分析，得到了下式的结果：

式中，ASAL(φ,λ)和pSAL(φ,λ) 为(φ,λ)的自吸引-负荷潮振幅和相位。而后，将ζMEM和刚刚得到的ζSAL运用到下一次计算，开始迭代。其中，ζMEM由下式给出：

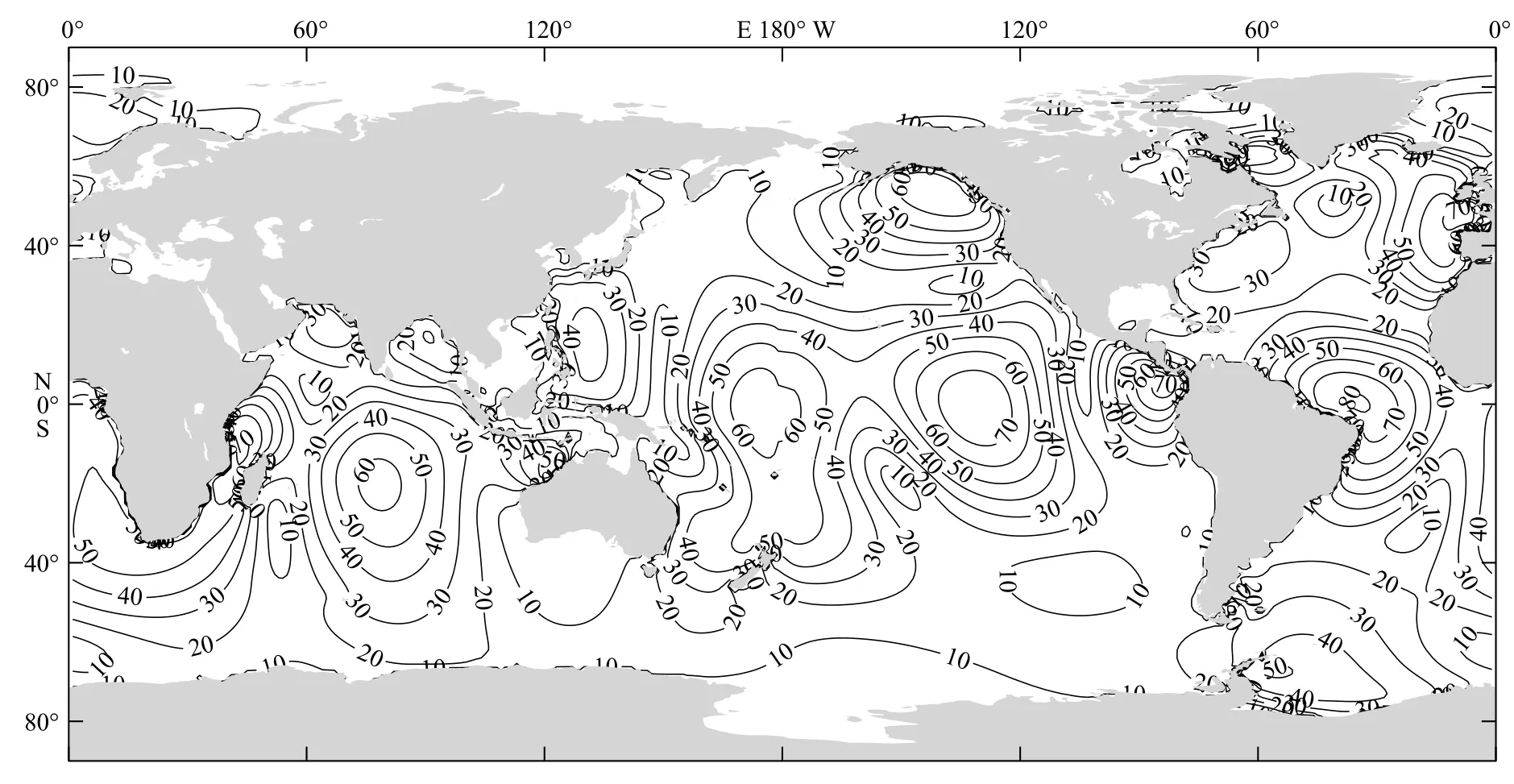
图4 本文模式计算得到的 M2分潮自吸-负荷潮等振幅线（单位：mm）Fig.4 Co-amplitude charts of M2 self-attraction and loading tide of the model in this paper (unit:mm)

图5 本文模式计算得到的 M2分潮自吸-负荷潮同潮时线（单位：（°））Fig.5 Co-phase charts of M2 self-attraction and loading tide of the model in this paper (unit:(°))

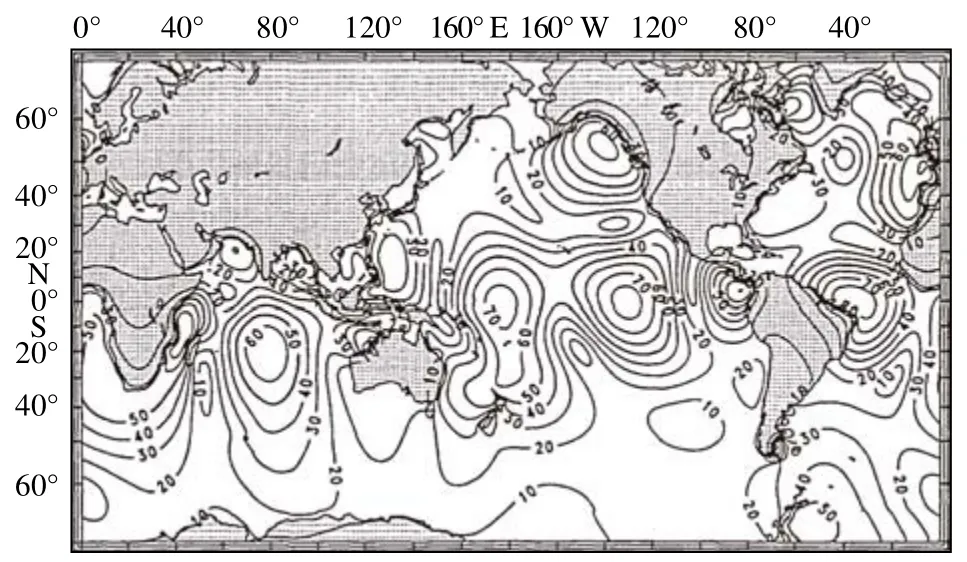
图6 M2分潮自吸-负荷潮等振幅线（据文献[12]，单位：mm）Fig.6 Co-amplitude charts of M2 self-attraction and loading tide (based on reference [12],unit:mm)

图7 M2分潮自吸-负荷潮同潮时线（单位：（°））（据文献[12]）Fig.7 Co-phase charts of M2 self-attraction and loading tide(unit:(°))(based on reference [12])

式中，ζPREVIOUS为 前一次迭代的水位计算结果，记忆效应机制ζMEM的加入可将前后两次迭代计算建立起联系，让迭代计算迅速收敛。实验结果显示，加入ζPREVIOUS后，两次迭代便可使实验结果达到最佳效果，迭代后M2分潮深海振幅均方根误差从7.68 cm 降为6.51 cm；浅海振幅均方根误差从22.1 cm 降为18.5 cm。

2.4 模型基本设置

计算网格节点总数为351 153，三角形个数为673 234，使用GEBCO 分辨率为1 min 的地形数据插值到网格点上得到水深。为了更好地对潮流能进行计算，计算网格在部分地形复杂的近海区域进行了加密，其网格分辨率可达2～5 km，而在大洋深海海域网格分辨率约为30 km。图8 为欧洲部分海域网格图，以英国为代表的欧洲各国是世界上潮流能最丰富的地区之一，本模式在该地区近岸海域分辨率达到了2～3 km。

图9 为美国东海岸部分海域网格图。美国东海岸地形复杂，包含圣劳伦斯湾、长岛海峡、特拉华湾等在内的众多重要海峡，本文模式在该地区的近岸分辨率达到了2～3 km。

图10 为加拿大北部部分海域网格图。加拿大北部海域有哈德森湾、巴芬湾以及西北航道。尤其是西北航道，作为是世界上最险峻的航线之一，地形复杂，海峡水道众多。本文模式在该地区海域进行了加密，近岸海域分辨率达到了2～4 km。

计算格式为内外模分离，外模时间步长为30 s，内模时间步长为120 s。计算时长为62 d，每隔1 h 输出一次运行结果，对最后40 d 的结果进行调和分析，由天体引潮力驱动，包括 M2、S2、N2、K1、O1、Q1共6 个分潮。天体引潮力驱动的平衡潮水位 ζEQ的计算方法由下式给出。

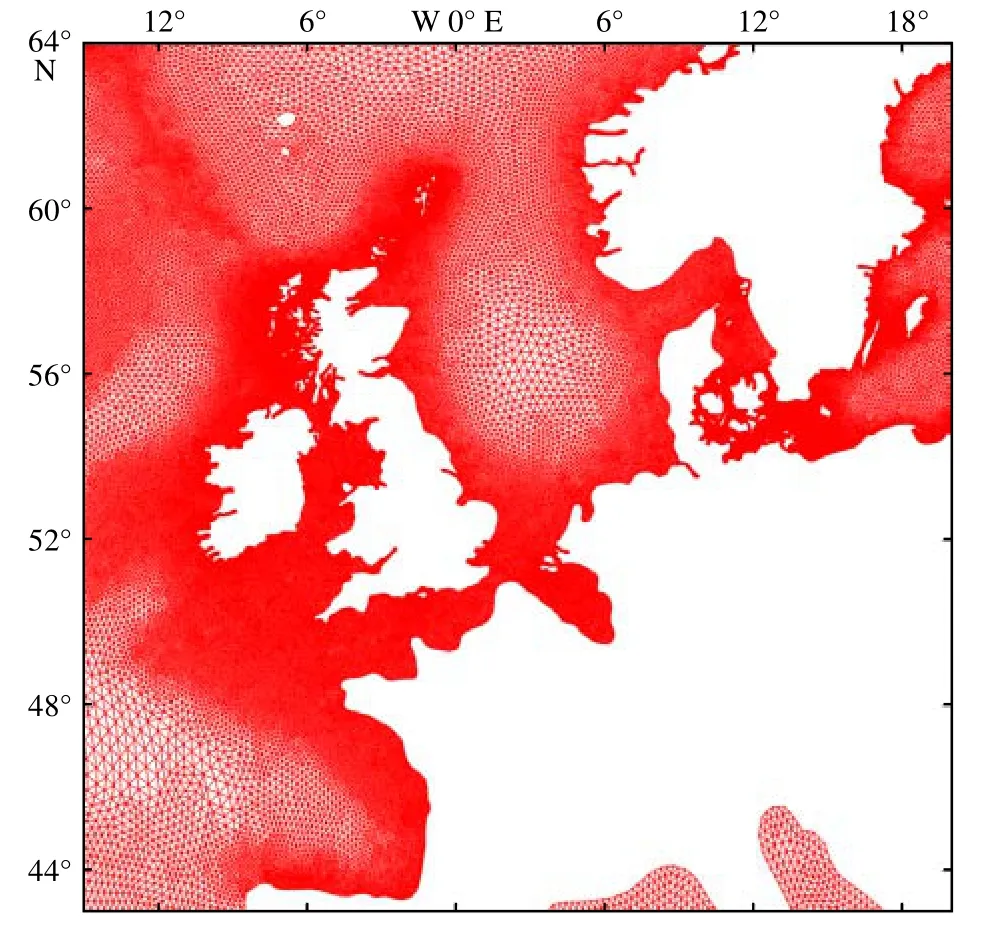
图8 欧洲部分海域网格图Fig.8 Grid map of European sea areas

图9 美国东海岸部分海域网格图Fig.9 Grid map of east coast of the United States

（1）对于半日潮而言

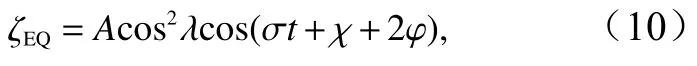
（2）对于全日潮而言

式中，λ为纬度；φ为经度；A为对应分潮振幅；σ为对应分潮频率；χ为对应分潮的天文相位，各参数具体取值如表2 所示。

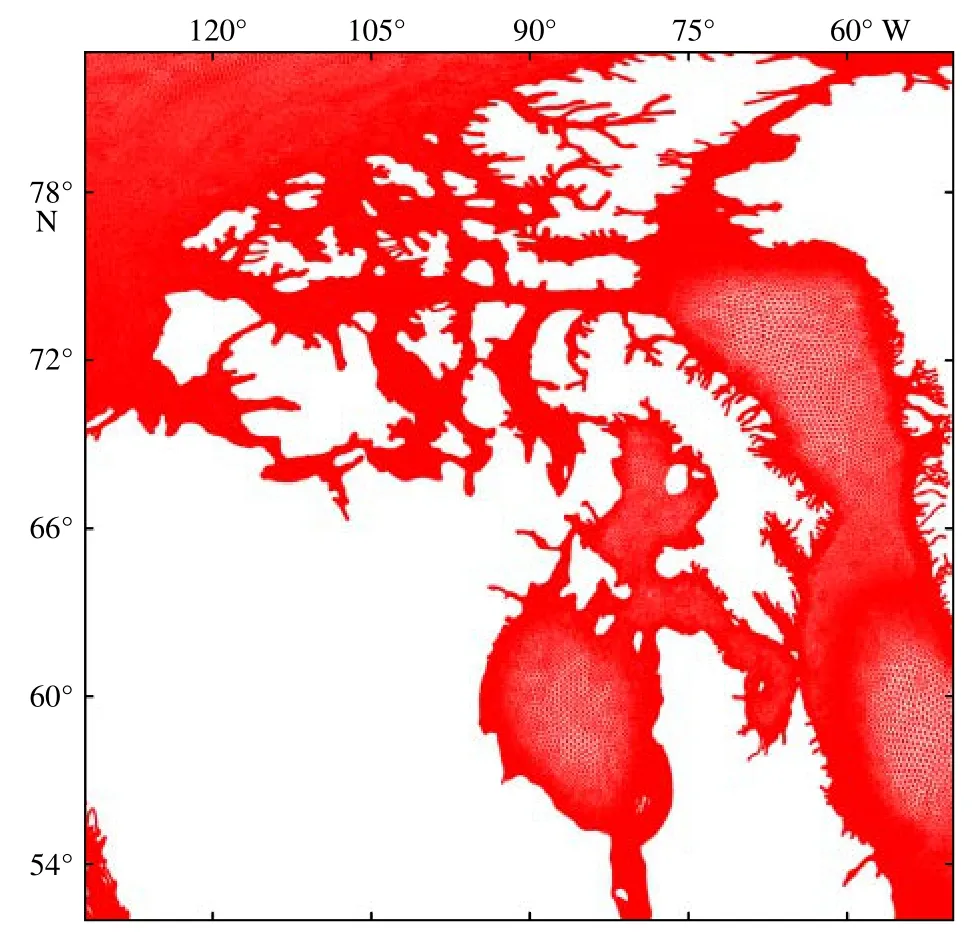
图10 加拿大北部部分海域网格图Fig.10 Grid map of northern Canada

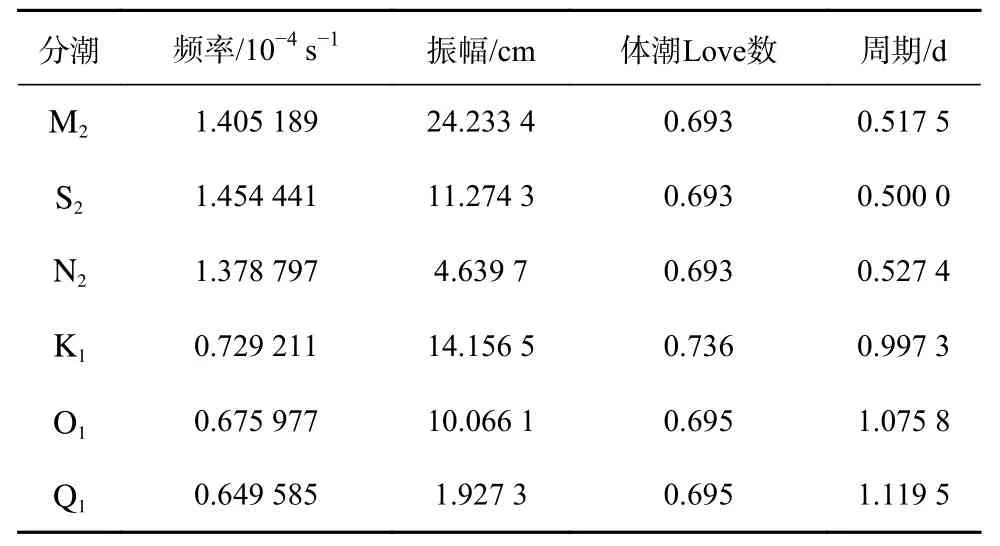
表2 模型中各分潮平衡潮水位参数Table 2 Constituent-dependent parameters in the model

3 模型验证与结果分析

3.1 模型验证

由于潮流本身的复杂性、观测的难度以及资料的不完整，目前正压潮汐模式普遍用潮位对模式进行验证，验证的对象为高分辨率的全球潮汐同化模式，原因有二：其一，大部分全球潮汐同化模式的潮位精确度已经超越了卫星高度计；其二，使用相同的全球潮汐同化模式使得大家有一个相同的比较标准，方便对比。本文采用TPXO.9 来验证潮汐振幅。由于不断更新的TPXO模型在全球海域远近海的潮汐结果准确性都在不断提高，所以对于大部分纯动力全球潮汐模型，普遍采用同化模型TPXO 来验证结果。为了方便对比，本文也不例外。本文用来计算均方根误差（RMSE）的公式为

式中，Ami和Aoi分别是网格点i处的本模型模拟的潮汐振幅和TPXO.9 在网格点i处的潮汐振幅；ai是网格点i所控制的网格面积。TPXO.9 的网格分辨率为（1/6）°，均匀分布在全球海洋，本文将模式所得结果插值到该网格上，然后与TPXO.9 的结果进行对比。

本文模型在全球范围内各分潮潮汐振幅模拟结果的RMSE 如表3 所示。目前其他几种应用较广的纯动力全球潮汐模型 M2分潮的RMSE 如表4 所示。

由本文模型计算得到的 M2分潮振幅RMSE 与Stammer 等[7]给出的常见纯动力全球潮汐模型的 M2分潮振幅RMSE 对比来看，本文模型的 M2分潮振幅RMSE在水深大于1 000 m 海 域为6.51 cm，仅次于OTIS-ERB模型的4.65 cm 和HIM模型的5.25 cm；在水深小于1 000 m海域为18.5 cm 略优于OTIS-GN 模型的18.6 cm，在上述模型中最低。可见本文模型在深海及近海都取得了良好的模拟结果，尤其是在近海海域，模型充分发挥了非规则网格在近海加密的优势，模拟较为精确，为近海海域潮流能的计算奠定了良好的基础。

表3 模型中各分潮振幅相对于TPXO.9 的均方根误差Table 3 The RMSE of tidal amplitudes relative to TPXO.9 in the model

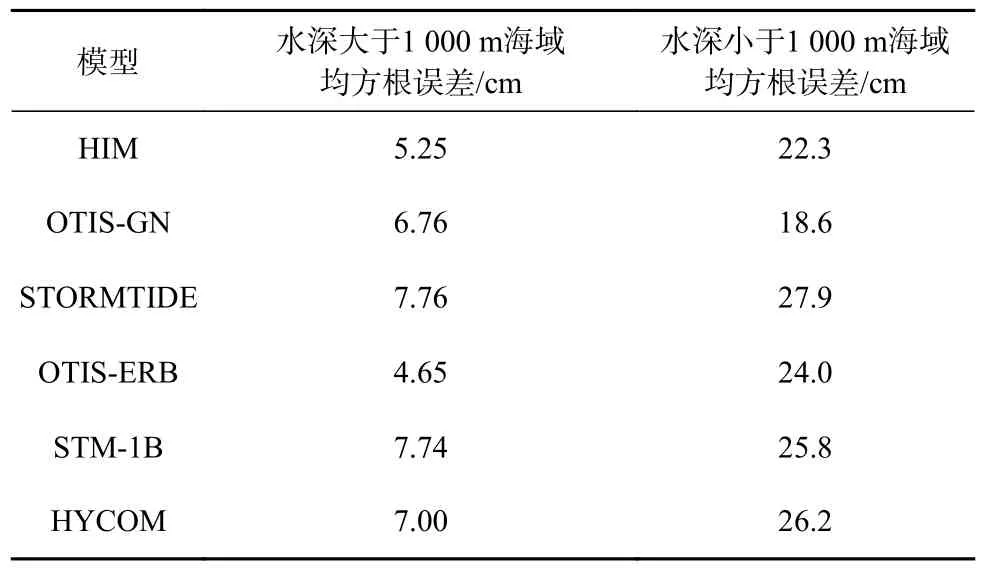
表4 常见纯动力全球潮汐模型 M2分潮振幅相对于TPXO.8 的误差[7]Table 4 The RMSE of M2 tidal amplitudes relative to TPXO.8 in other common forward models[7]

3.2 同潮图分布特征

利用模式结果将 M2、S2、N2、K1、O1、Q1共6 个分潮进行调和分析，绘制同潮图，本文展示其中振幅较大的M2分潮（图11）和 K1分潮（图12）的同潮图。由图11可见，本模式较好地再现了 M2分潮在太平洋的5 个无潮点，其中靠近北侧的两个无潮点纬度分别为29°N和赤道附近，这两个无潮点离近岸相对较近，其余3 个无潮点位于南太平洋；大西洋有4 个无潮点，南北半球各两个，北半球的两个无潮点在48°N 和18°N，后者位于加勒比海和北大西洋东北交界处；印度洋有2 个无潮点，分别位于赤道附近和32°S，后者靠近澳大利亚西南海岸。从全球范围来看，M2振幅较大的海域主要集中在近海，在北大西洋北部欧洲西海岸和加拿大的东北海域 M2振幅达到了1.5 m 以上；大洋地区 M2分潮振幅较小，基本与天文引潮力潮高相同。

图12 为模型计算的全球 K1分潮同潮图。K1分潮潮波结构相对比较简单，在太平洋存在4 个无潮点，大西洋和印度洋各有3 个。振幅较大海域主要在太平洋北部边界及东南亚等一些发生共振的海湾处，如北部湾、泰国湾等；大西洋振幅较小，大部分海域都在10 cm 以下；印度洋西北海域振幅偏大，在亚丁湾、阿曼湾振幅达到了35 cm 以上；南半球相对北半球振幅较小。

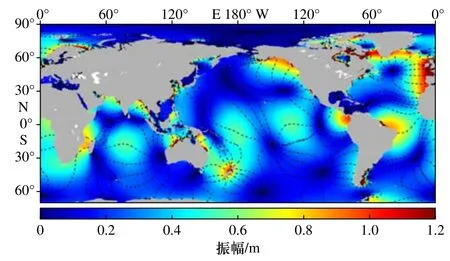
图11 本文模型计算的全球 M2分潮同潮图Fig.11 Global M2 co-tidal map of the model in this paper

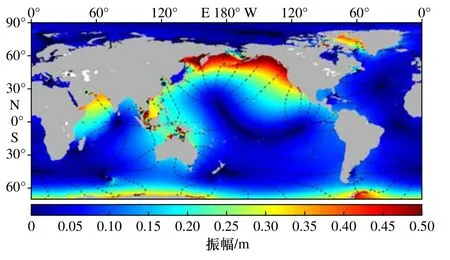
图12 本文模型计算的全球 K1分潮同潮图Fig.12 Global K1 co-tidal map of the model in this paper

4 潮流能计算与主要潮流能分布

4.1 潮流能计算方法

本文采用张理和李志川[3]提及的潮流能密度来统计全球潮流能，潮流能密度是指通过单位面积的潮流能量，定义为

本文所计算的为平均潮流能密度，计算公式为

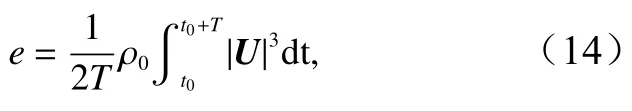
由此得到周期T内的平均潮流能密度；t0为初始时刻；T为评估周期，本文取为7 d，采样间隔为30 min。

实际计算公式为

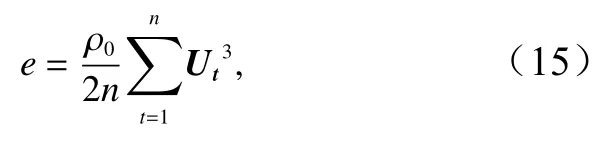
式中，n表示评估周期内的流速采样个数，为336。

4.2 全球主要潮流能分布状况

4.2.1 英国沿海潮流能分布

图13 为英国沿海潮流能分布。英国是潮流能最丰富的国家之一，其沿海的潮流能十分丰富，多处潮流能带潮流能密度超过了200 W/m2。其中，英吉利海峡的潮流能带面积极大，拥有面积接近33 000 km2的连续大潮流能带，大部分区域潮流能密度普遍超过600 W/m2，最大潮能流密度达到1 100 W/m2；英国北端海峡处大潮流能带面积较小，但最大潮流能密度也超过了1 000 W/m2。同时，在英国以西及爱尔兰以北海域也有多处大潮流能带，爱尔兰海中部最大潮流能密度超过了350 W/m2，爱尔兰东北海域最大潮流能密度超过了270 W/m2，圣乔治海峡东侧最大潮流能密度也达到了240 W/m2。本文所给出的英国沿海潮流能分布的大潮流能带位置与Iyer 等[16]文中图4 给出的大潮期间英国沿海潮流流速峰值分布的潮流流速较大的位置十分吻合，说明本文模式及计算方法能较好地得到大潮流能带的位置。

4.2.2 加拿大东北海域潮流能分布

图14 为加拿大东北海域潮流能分布。加拿大东北海域潮流能十分丰富，结果显示在巴芬岛西侧海域有大片大潮流能带，最大潮流能密度超过了1 150 W/m2，该潮流能带平均潮能流密度也达到了700 W/m2；在南安普顿岛西北侧海域海峡地带也存在两块高潮流能带，最大潮流能分别达到了1 800 W/m2和500 W/m2；同时在哈德逊海湾东端入口处有超过500 W/m2的潮流能带，南端海湾口处有超过800 W/m2的潮流能带。加拿大东北海域潮流能十分丰富，有多处大潮流能带，且地理环境优越，十分适合潮流能开发。

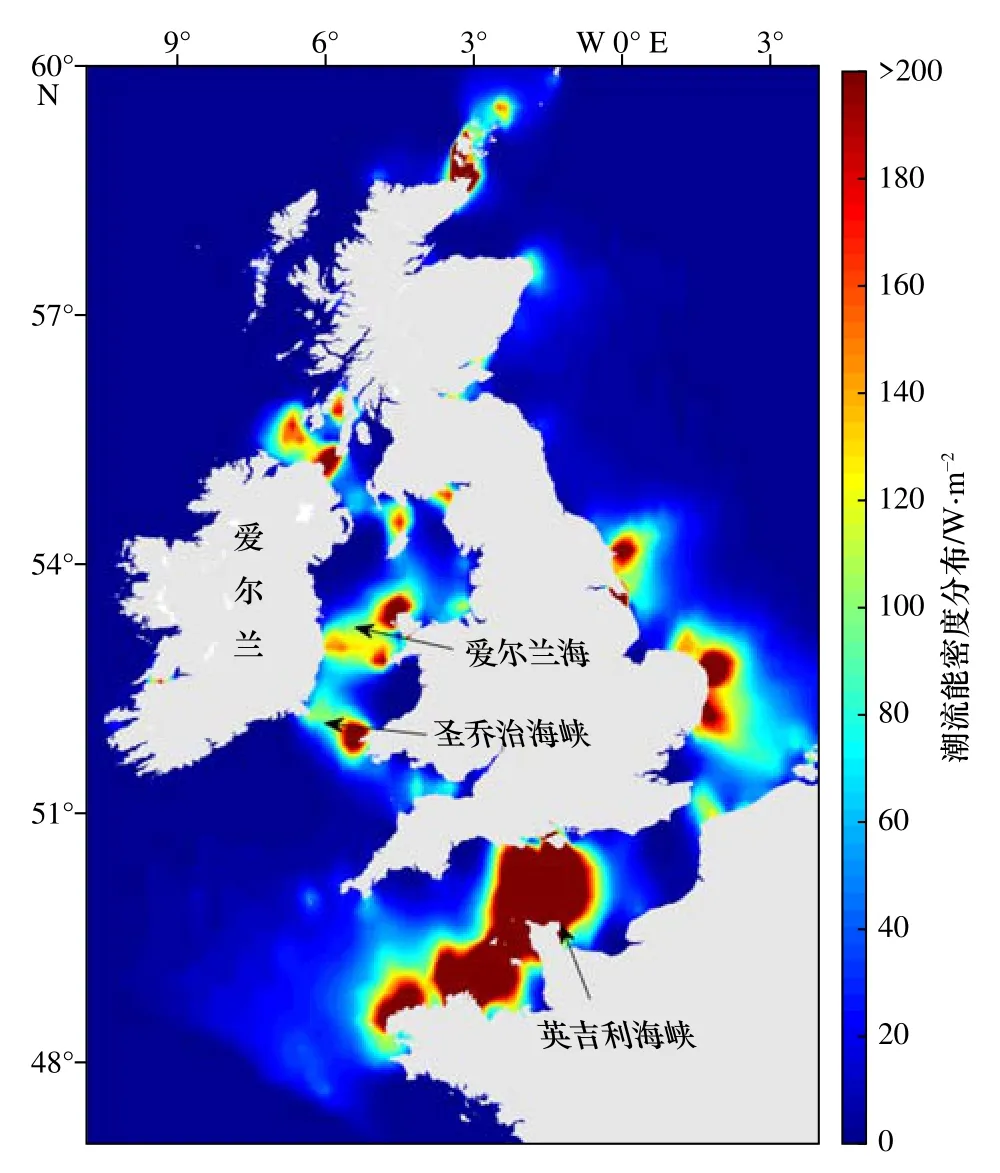
图13 英国沿海潮流能密度分布Fig.13 Tidal current energy distribution of the British coast

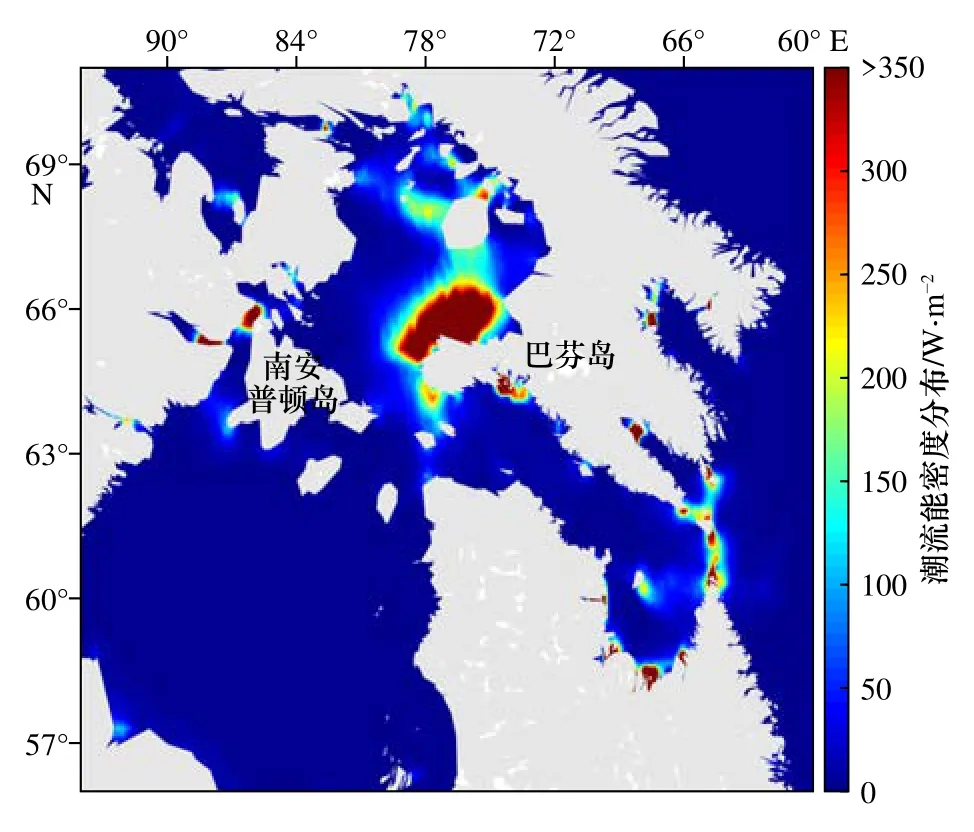
图14 加拿大东北海域潮流能密度分布Fig.14 Tidal current energy distribution of the northeastern Canada coast

4.2.3 俄罗斯西北部海域潮流能分布

图15 为俄罗斯西北部海域潮流能分布。在俄罗斯西北部海域的白海入口处和切沙湾海域存在大潮流能带，最大潮流能密度分别达到了500 W/m2和260 W/m2。尤其在白海入口处面积近18 000 km2海域内几乎都为大潮流能带，平均潮流能密度超过280 W/m2，可以进行大规模的潮流能开发项目。

4.2.4 阿拉斯加沿海潮流能分布

图16 为阿拉斯加沿海潮流能分布。阿拉斯加沿海有两块大潮流能带，分别位于布里斯托尔湾和库克湾海域，都分布在海湾靠近湾顶海域，最大潮流能密度分别达到了200 W/m2和500 W/m2，尤其在库克湾湾顶处，潮流能储量十分巨大，且靠近陆地，潮流能的开发条件十分优越。

4.2.5 澳大利亚北部海域潮流能分布

图17 为澳大利亚北部沿海潮流能分布。澳大利亚北部沿海有多处能流密度超过100 W/m2的潮流能带，其中，长岛周边海域最大能流密度达到了280 W/m2。澳大利亚北部海域岛屿众多，为潮流能聚集提供了得天独厚的条件，在众多岛屿周边、海峡及水道处都存在许多潮流能带，虽然面积不大，但十分密集、潮流能密度大且分布在岛屿和陆地周边，对潮流能开发十分有利。

图15 俄罗斯西北部海域潮流能密度分布Fig.15 Tidal current power distribution of the Northwestern Russia coast

图16 阿拉斯加沿海潮流能密度分布Fig.16 Tidal current power distribution of the Alaska coast

4.2.6 中国近海潮流能分布

图18 为中国近海潮流能分布。中国近海潮能分布显示，台湾海峡南端有大潮流能带，数据显示最大潮流能密度达到130 W/m2，同时，台北北侧海域和长江口杭州湾海域潮流能密度达到了90 W/m2，在朝鲜西侧海域也有最大潮流能密度为60 W/m2的潮流能带。其中长江口杭州湾、台湾岛北端以及朝鲜半岛西侧都具有近岸水深较浅的良好潮流能开发条件。将本文所得结果与张理和李志川[3]给出的我国近海潮流能年平均功率密度分布相比较，所给出的大潮流能带位置基本一致，量值稍有差异，进一步说明本模式及计算方法能较好地得到大潮流能带的位置，初步分析量值上的差异主要还是由于本文利用垂向平均流速来计算潮流能密度与实测流速有所差异以及模型网格的分辨率和岸线不够精细造成的。

图17 澳大利亚北部沿海潮流能密度分布Fig.17 Tidal current power distribution of the Northern Australia coast

图18 中国近海潮流能密度分布Fig.18 Tidal current power distribution of the China coast

5 结论

本文利用FVCOM 数值模式，自行加入了内潮耗散模块及自吸引-负荷潮严格处理模块，充分发挥非规则网格在处理极点问题的优势，使模式实现在全球范围内真正脱离外部数据，完全由天体引潮力驱动全球潮汐运动。在模拟全球潮波的基础上，利用能流密度计算公式，评估了全球范围内潮流能及大潮流能带的位置分布。针对潮流能的统计结果显示，全球范围内，大潮流能带大都位于海峡、海湾湾顶以及水道等水深较浅、地形狭窄的沿海地带。英吉利海峡处存在面积接近33 000 km2，最大潮流能密度达到1 100 W/m2的大潮流能带，同时英国周边海域也有多处潮流能带的最大潮流能密度处于200～300 W/m2；加拿大巴芬岛西侧海域最大能流密度超过了1 150 W/m2；阿拉斯加沿海库克湾海域最大潮流能密度达到了500 W/m2，整块潮流能带面积接近24 00 km2；俄罗斯白海入口处潮流能带面积较大，最大潮流能密度达到了500 W/m2；澳大利亚沿海大潮流能带面积虽不大，但数量众多，且潮流能密度普遍超过了100 W/m2；中国近海在长江口杭州湾海域以及台北以北海域潮流能密度达到了100 W/m2。

潮流能作为海洋能的重要组成部分，近些年潮流能的开发在世界范围内取得较大进步。但在国际上迄今尚未系统地绘制出全球潮流能资源分布，本文基于模式，初步计算出全球潮流能流密度，获得潮流能在全球海域总体分布状况，为潮流能的开发选址提供指导。由于海域地形和岸线对潮流模拟的影响显著，在接下来的工作中将进一步发挥非规则网格的优势，细化网格在近岸地区的分辨率，使网格能应用更精细的岸线及近岸水深数据，进一步提高模式在近岸地区的模拟精度，同时也将尝试将三维斜压过程加入到模式过程中，使潮流的模拟更加贴合实际。