客车减振器支架疲劳寿命仿真分析及验证

董晓坤， 张保锋

(郑州宇通客车股份有限公司， 郑州 450000)

随着客车产品轻量化需求逐步提升，关键零部件的可靠性、耐久性愈发受到挑战[1]。通过台架试验及整车可靠性试验来验证关键零部件的可靠性、耐久性，周期偏长且成本高[2]。验证失效后还需要多轮优化及实物验证，严重影响产品快速开发上市。

静强度分析通过安全系数来平衡轻量化及结构可靠性，仅能定性判定；若对轻量化水平要求偏高，势必会影响安全系数余量。通过疲劳仿真分析，能充分考虑载荷的频次信息，且可参考企业依据的实物台架试验标准来判定是否合格。

疲劳损伤主要分为线性疲劳累计损伤、修正的线性疲劳损伤及非线性疲劳累计损伤。本文以Miner线性累计损伤[3]来进行减振器支架的高周疲劳寿命研究。

1 有限元模型建立及赋值

1.1 有限元模型

采用Altair公司的Hyperworks软件，建立某减振器支架的有限元模型。减振器支架有限元模型内部采用solid单元，考虑疲劳失效通常从零部件表面开始，solid单元的表面保留一层shell单元(厚度0.1 mm)。除shell单元的厚度为0.1 mm外，单元网格其余尺寸均为3 mm。原则上关键部位细节特征(如圆角)需保留，且整体网格过渡平滑，网格质量达标。

减振器支架有限元模型共223 647个单元，共 45 230个节点。其中solid单元201 306个，shell单元22 341个。

1.2 赋加载荷及约束

按照汽车行业减振器台架试验方法[4]，结合客车减振器支架耐久性要求开展实物台架试验。减振器支架台架试验时通过4个螺栓将其连接到夹具上，再用作动器进行加载。初步设定加载载荷范围为15～30 kN，实际加载载荷根据静强度分析应力水平确定，确保其应力水平在高周疲劳范围内。本文静态分析实际加载为25 kN，疲劳仿真分析采用单位正弦波激励进行应力转换。加载方向与实际减振器轴向一致。其有限元模型在所有螺栓孔处创建RBE2刚性单元，6个自由度全约束。具体如图1所示。

1.3 材料参数及S-N曲线

减振器支架材料为ZG310-570，它是以碳为主要合金元素并含有少量其他元素的铸钢，强度大，硬度高。基于试验获取的该材料抗拉强度为670 MPa。根据机械设计手册[5]及企业积累数据，ZG310-570材料的拉压疲劳强度σ-1与抗拉强度σb的关系式为σ-1≈0.34σb，即该材料疲劳强度值σ-1=227.8 MPa。

疲劳寿命曲线主要表征材料在不同应力和应变水平下发生疲劳破坏时的疲劳寿命[6]，分为低周疲劳、高周疲劳及无限寿命曲线。低周疲劳(N<104)通常用应变-寿命(ε-N)曲线方程表示，高周疲劳(N≥104)通常用应力-寿命(S-N)曲线方程表示，无限寿命为应力小于或等于疲劳强度的一条直线表示。

在OptiStruct中，高周疲劳应力-寿命(S-N)曲线方程的定义为

S=S1×Nb，N≥104

(1)

式中:S为疲劳应力；S1为寿命次数N=100时对应的疲劳应力值；N为寿命次数；b为疲劳强度指数。

OptiStruct中，钢材S-N曲线方程的b=-0.125，疲劳强度极限寿命Nc1=1×106，即当疲劳应力S=σ-1=227.8 MPa时，对于ZG310-570材料，N=Nc1=1×106。根据式(1)可求得S1=S/Nb=227.8/(106)-0.125=1 281 MPa。

即OptiStruct中ZG310-570钢材的S-N曲线方程可表示为

(2)

按照汽车行业约定，通常以材料的疲劳极限强度对应寿命为1×107次作为基准，则S1=S/Nb=227.8/(107)-0.125=1 708 MPa，即修正后的ZG310-570钢材的S-N曲线方程为

(3)

2 疲劳仿真分析及验证

线性疲劳累积损伤理论认为，零部件在不同的应力水平级数上的损伤是能够进行线性求和的，而且与载荷顺序没有关系，只与载荷大小有关。

零部件在一个低于材料屈服极限载荷作用下经过一定循环次数之后，会使结构产生失效[7]。但只要输入载荷比材料的疲劳极限大，每一次输入载荷都会对零部件产生疲劳损伤。若材料在某常幅的载荷下的循环寿命为N，那么计算每一个循环的损伤为1/N，在相同幅值输入载荷循环作用n次后，材料累积的损伤就是C=n/N[8]。

疲劳分析是根据疲劳载荷历程和静态载荷历程的关系，基于线性迭代方法，对静态分析得到的应力时间历程进行转化得到疲劳时使用的应力时间历程[9]。

用OptiStruct求解器对有限元模型进行静强度分析及疲劳分析。静强度分析中，加载25 kN对应的减振器支架最大应力在一个螺栓连接处，其值为286 MPa。疲劳分析中，在静态应力的基础上，输入单位幅值的正弦波载荷谱激励进行疲劳应力转换，且不对其进行比例放大及相位偏移补偿。得到的正弦波疲劳应力幅值与静强度最大应力值相同，即为286 MPa，高于σ-1值，低于式(3)中N=104时对应的疲劳应力值540 MPa，所以按照高周疲劳应力-寿命曲线方程(3)开展疲劳分析。

按照Miner线性累计损伤进行疲劳分析，基于OptiStruct软件，将一个周期的正弦波疲劳应力谱等步长离散成约100个疲劳应力点进行累计疲劳损伤计算，得到减振器支架最薄弱部位的疲劳寿命为 13 340次，该最薄弱位置在一颗螺栓连接处，与静态应力最大位置相同。如图2所示。

图2 减振器支架疲劳寿命分析结果

选取6个相同规格的减振器支架，开展实物台架试验。减振器支架在试验过程中均发生失效，失效寿命次数分别为10 146、11 584、11 805、15 037、16 688及19 922,失效位置与仿真分析中最薄弱部位一致，未满足10万次实物台架试验标准要求。具体如图3所示。6个失效寿命次数的平均值与上述仿真分析疲劳寿命值之差约6%，一定程度验证了仿真分析的有效性。

图3 减振器支架台架试验失效位置图

另外，还可以利用上述6个试验数据进行减振器支架的B50寿命计算，具体过程如下。

汽车底盘零部件(包括减振器支架)的台架试验通常都符合威布尔分布[10]。首先，根据6个试验疲劳寿命计算每个疲劳寿命的不可靠度概率观测值；然后采用最小二乘法拟合求解威布尔分布可靠度概率方程中的参数，并判定6个试验数据符合威布尔分布的置信区间；最后，计算减振器支架的B50(50%可靠度概率)寿命值。

在计算不可靠度概率观测值时，先将样本数据按照从小到大的顺序排列，即

t1≤t2≤……≤tn

(4)

由于本次试验只有6组试验数据，样本量较小，按照式(5)[10]计算6个台架试验疲劳寿命ti对应的不可靠度概率观察值F(ti)：

F(ti)=(i-0.3)/(n+0.4)(i=1,2,…,n)

(5)

式中：i为按式(4)排列的每个台架试验疲劳寿命对应的秩序(从小到大)；n为减振器支架台架试验数量，即n=6。

机械工程领域中的威布尔可靠度概率分布定义方程[10]如下：

R(t)=e-(t/b)k

(6)

根据式(5)得到不可靠度概率F(t)的分布方程：

F(t)=1-R(t)=1-e-(t/b)k

(7)

式中：R(t)为可靠度概率；t为疲劳次数；k为形状参数指数，表征故障率随时间增加；b为尺寸参数，与平均寿命和工作条件负载有关。

绘制减振器支架台架试验F(t)-t分布图，如图4所示。

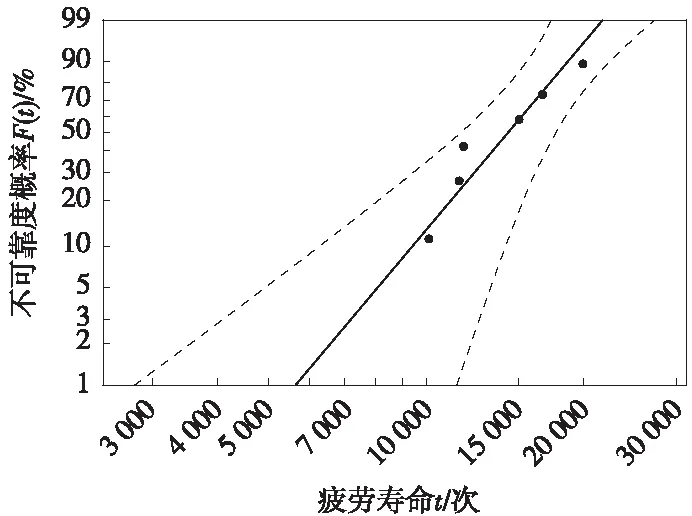
图4 减振器支架台架试验F(t)-t分布图

图4中6个离散小圆点为台架试验寿命ti及按式(5)计算对应的不可靠度概率观测值F(ti)，左右辅助虚线为95%置信区间下F(t)-t分布上下限，实线为拟合的F(t)-t分布线。6组台架试验数据位于两条辅助虚线范围内，符合威布尔分布。

对按照式(5)计算得到6个F(ti)数据。依据式(7)进行最小二乘法拟合，可得到式(7)中的k=4.553，b=15 553。

上述参数代入式(7)后，得到：

R(t)=e-(t/15 553)4.553

(8)

按照式(8)，得到可靠度概率R(t)=50%时，减振器支架寿命值t=14 345次，即该减振器支架的B50寿命为14 345次。

3 结束语

本文的研究为疲劳仿真分析提供一种方法。后续跟踪及对标其他种类零部件计算分析及试验结果，逐步形成分析评价数据库，切实提升零部件设计水平。