齐大山露天矿高陡边坡动态预警方法研究

孙铭辰，孙厚广，钟小宇，曹 旺，陈晓青

(1.辽宁科技大学 矿业工程学院，辽宁 鞍山 114051； 2.鞍钢矿业集团公司，辽宁 鞍山 114051；3.东北大学 资源与土木工程学院，辽宁 沈阳 110819)

露天矿边坡稳定性动态分析是了解开采过程中坡体演变过程[1]，并为边坡所处的安全状态和失稳预测提供可靠数据的科学方法[2-5]。通过边坡监测信息[6-8]了解岩土体变形的范围和演化趋势[9]，合理预测边坡可能发生破坏的时间和空间[10-14]，以便于及时采取措施，确定优化方案，合理解决边坡失稳破坏问题。

目前采用传统的极限平衡方法进行边坡稳定性分析时，由于其模型仅考虑边坡形态、力学参数对坡体稳定性的影响[15]，无法反映边坡开挖卸荷作用对边坡安全系数的影响[16]，因此，笔者在分析露天矿边坡开采过程中的稳定性时，不仅考虑坡体形态变化，还考虑开挖卸荷对岩体的劣化作用，并结合现场变形监测信息对坡体的稳定性进行动态预测评价。

1 边坡稳定性分析方法

由于露天矿边坡在频繁爆破开采过程中，边坡形态与力学参数长期处于动态变化过程中，因此笔者结合岩体劣化本构模型[17]与强度折减法[18]，提出一种边坡动态稳定性的分析方法。

1.1 岩体劣化本构模型

(1)

在开挖卸荷后岩体应力重新分布，内部原生裂隙不断扩展，这些细观裂隙的发育扩展[20]导致边坡发生垮塌现象。因此，可以认为原生裂隙的二次扩展和新裂隙萌生过程是岩体微观结构不断分离、连通的过程，在这一过程中，岩体黏聚力C、内摩擦角φ与抗拉强度T不断降低。即表明在该脆性岩体劣化本构模型中，岩体各力学参数均是关于等效塑性应变的变化函数，通过室内试验和反分析可以将其简化为线性分段函数，见图1。图1中φd为卸荷后岩体残余内摩擦角，Cd为卸荷后岩体残余黏聚力，Td为卸荷后岩体残余抗拉强度。

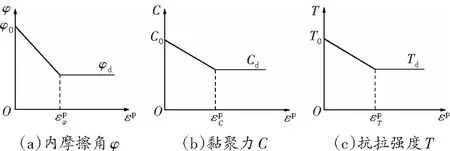
图1 岩体卸荷区力学参数劣化过程

在该模型中，每一时步计算中模型的力学参数均需根据等效塑性应变的变化情况进行动态调整，并采用Mohr-Coulomb屈服准则作为其剪切屈服函数。进入屈服状态后的岩体力学状态随等效塑性应变不断变化，屈服面也是等向或沿等倾线动态变化；同时将岩体内部原生裂隙对岩体强度的干扰纳入考虑范围，调整最大主应力强度准则，由于抗拉强度也是以等效塑性应变为基础定义的动态函数，故可通过计算分析反映不同状态下微观裂隙的萌生、扩展对岩体强度的影响，最终在FLAC平台上调用CRDM.dll动态链接库文件进行模拟。

1.2 强度折减法

Griffiths等提出的有限元强度折减法理论主要采用Mohr-Coulomb本构模型，即利用C和φ两个强度指标来代替岩体力学特性参数，且利用一个折减系数Fs对C和φ两个参数进行折减来获取平面应变问题中的最小安全系数，可分别由式(2)和式(3)求得参数C′和φ′并取代原参数，直至计算收敛。而弹性模量E、泊松比μ在计算中假设为定值，不随C、φ的改变而变化。

(2)

(3)

式中：C′为折减后黏聚力；φ′为折减后内摩擦角；F为折减系数。

强度折减法的实质就是通过折减岩体抗剪强度，使得最大抗剪强度线性函数逐渐向岩体莫尔应力圆靠近的过程，当两函数处于相切状态时，岩体的安全系数即可用此刻的折减系数Fs来表述。

由于岩体力学参数随着开挖的进行而动态变化，因此在利用强度折减法分析时，边坡的岩体参数随着开采状态动态调整。其中在FLAC软件中，通过强度折减收敛得到安全系数时需先利用RDM本构模型获取模型中所有单元的力学参数，然后再将单元参数自动赋予边坡计算模型中，最后实现边坡稳定性分析。

2 齐大山露天矿边坡稳定性动态预警方法

2.1 露天矿概况

齐大山露天铁矿是亚洲最大的露天矿，其边坡全貌如图2所示。该矿位于鞍山市的东北郊千山区调军台村，矿床的大致走向为西北—南东向，现已经开采至-243 m，其封闭圈的标高为+42 m，矿坑南北长度为3 400 m，矿坑的宽度大约为1 000 m。原一期到界边坡长度1 540 m，边坡标高+30～-187 m，最大边坡高度220 m，边坡角35°32′。

图2 齐大山露天矿边坡全貌

采场南采区东帮边坡，二期扩建到界边坡长度1 370 m，边坡标高+154～+76 m，边坡高度78 m，边坡角32°10′，边坡岩性主要为第四系、混合岩、石英绿泥片岩。采场西帮边坡长度1 930 m，边坡标高+42～-30 m，最大边坡高度72 m，边坡角38°69′。边坡岩性主要为第四系千枚岩。目前该矿进入扩帮开采期，其边坡稳定性是安全生产的重要保障，因此对其进行稳定性评价至关重要。

2.2 露天矿边坡稳定性实时监测

由于齐大山露天矿坑东北帮区域稳定性较差，在扩帮期间出现了几次小型破坏，因此根据工程需要在该区域布设了3个GPS监测点，如图3所示。

图3 边坡监测点

3个监测点于2018年10月15日开始采集变形监测数据，变形观测周期设置为2 h，结果见图4。

图4 滑坡变形监测数据

由图4可以看出，利用GPS对边坡进行了长达近一个月时间的连续监测，由于监测点3边坡下部扩帮工程持续进行，导致监测点3的变形持续增大，在10月15日至10月30日期间，该监测点变形始终保持6.5 mm/d的变形速率，在10月30日前后，变形量累计为8 cm，但此时监测点1和监测点2的变形速率十分稳定，而且其变形值仅为2～3 mm(图5中曲线基本重合)。以上数据可以表明监测点3附近的边坡在扩帮过程中，存在潜在失稳的可能性。

在10月30日至11月6日期间，监测点3的变形进一步增大，而且变形速率较之前线性增长阶段大大提高，其中11月1日至11月6日变形速率分别为50.4、40.7、78.3、91.7、156.0、176.0 mm/d,截至11月6日，该点处的空间变形量累计已超过 1 m。参考前述同类岩质边坡失稳案例，当位移速率为10～100 mm/d时，边坡发生滑坡的概率较大，因此可以判断齐大山露天矿东北帮边坡已经达到失稳的临界状态。

2.3 露天矿边坡稳定性动态预警方法

露天矿边坡开采卸荷过程是复杂的多空间、时效性强的系统工程，且具有难度自增等特点，主要表现在开挖深度增加和开挖尺寸增大等条件下岩体潜在滑移面裂隙演化发育变化情况复杂，无法简单利用显式数学函数关系来反映开挖引起的边坡位移量值与边坡安全系数Fs之间的变化规律。为了更准确反映边坡岩体位移量和安全系数的关系，采用人工神经网络(Artificial Neural Network，简称ANN)，以实现预测未知数据来分析边坡岩体位移与安全系数之间的变化规律，并得出两者的非线性函数关系。

为获得边坡位移与安全系数的非线性映射关系，可按如下步骤依次进行：

1)将抗剪强度参数C、φ值作为模型主要影响因素构建参数组合表，并结合ANSYS、FLAC3D等数值计算软件获得监测点的变形位移值D的信息，从而建立人工神经网络学习初始可靠样本；

2)将位移值D和抗剪强度参数C、φ分别作为神经网络的输入向量和输出向量进行迭代收敛，并训练神经网络；

3)当获得成熟、准确的网络结构和训练次数时，即表示成功建立了具有高强度非线性映射关系的边坡实测位移值D与边坡动态安全系数Fs的神经网络模型；

4)将露天矿开采过程中的边坡实测位移值D作为输入向量，即可通过神经网络获得露天矿开采卸荷过程中边坡动态抗剪强度参数C、φ值；

5)将获得的每组抗剪强度参数C、φ值代入数值计算软件做一次正向计算，即可获得露天矿开采过程中边坡的动态安全系数Fs。

由上述步骤即可建立露天矿开采过程中边坡实测位移值D与边坡动态安全系数Fs的一一对应的样本空间。并进一步建立FLAC3D数值计算二维模型，如图5所示。

图5 边坡二维计算模型

利用Hoek-Brown强度准则计算可得岩体抗剪强度参数范围,如表1所示。

表1 岩体力学参数范围值

根据前文所述流程，通过FLAC3D数值计算构造不同岩体下边坡位移的神经网络样本空间。利用神经网络建立露天矿开采过程边坡位移与黏聚力、内摩擦角非线性映射的神经网络。将现场实测位移值输入进网络中，获得动态黏聚力和内摩擦角，再将其作为抗剪强度参数通过FLAC3D进行正向运算，得到对应的边坡安全系数Fs。

按照前述所示流程，以边坡位移值为输入，安全系数为输出，对神经网络进行迭代收敛训练后，可获得露天矿开采过程边坡位移与动态安全系数非线性映射的神经网络，将现场实测位移值输入到神经网络，得到露天矿边坡水平位移与动态安全系数之间关系曲线，如图6所示。

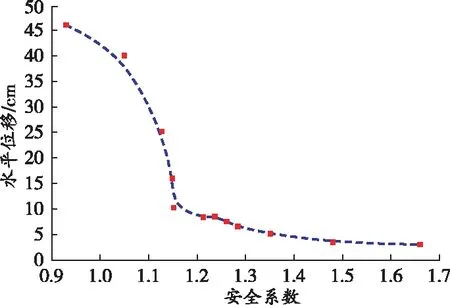
图6 露天矿水平位移与安全系数的关系曲线

根据上述研究成果，并结合现场边坡表面的位移监测结果确定了齐大山露天矿边坡稳定性的评价指标，见表2。根据齐大山露天矿扩帮过程边坡稳定性分析与预警指标，在边坡进入到临界状态时，需要停止扩帮作业，全面勘查边坡的具体形态，明确何种原因导致边坡变形持续增大，必要时根据工程进度与开采情况进行边坡处理。如果边坡达到失稳临界状态，则须及时停止作业，并清退现场作业人员和机械设备，待查明原因并处理后再重新进行开采作业。

表2 齐大山露天矿边坡预警指标

3 结语

1)依据现场变形监测，利用神经网络与数值模拟方法设计一套基于边坡变形的安全系数动态评价方法，可以实现边坡的实时预警。

2) 边坡动态预警方法结合岩体损伤力学本构模型，通过力学计算判断边坡岩体力学状态,再利用强度折减法对边坡的稳定性进行动态实时评价。在计算时边坡的岩体参数随着开采状态而动态调整。

3)建立了露天矿开采过程边坡位移与动态安全系数一一对应关系。在位移值增大初期，安全系数迅速减小，中期减小速率趋于平缓，后期减小速率逐渐加快。