基于UWB的矿井巷道精准三维定位系统设计

2020-12-31沈国杰周德胜郑雪娜

矿业安全与环保 2020年6期

沈国杰，周德胜，郑雪娜，李敏

(1.重庆水利电力职业技术学院，重庆 402160； 2.中煤科工集团重庆研究院有限公司，重庆 400039；3.重庆大学城市科技学院，重庆 402167)

煤矿井下人员和设备的精确定位是当今煤炭领域的热门研究课题，是矿井工人生命安全和设备资产安全的重要保障[1]。近年来，物联网、人工智能技术在煤矿安全生产中迅速展开应用，尤其是智能开采、机车无人驾驶、机器人自动巡检等技术的突飞猛进，对井下定位的精度和实时性都提出了更高的要求，传统的井下定位系统已经不能满足技术革新的需求[2]。

煤矿井下巷道弯曲、倾斜、表面粗糙，围岩介质复杂，金属铆钉、钢网众多，电缆管道布局繁杂，无线信号传输时存在严重畸变和衰减，常见的基于信号强度和基于角度测量的定位算法不适用于井下人员和设备定位[3-4]，而基于时间测量的定位算法测量精度只与信号传输时间有关，非常适合应用于煤矿巷道等封闭空间的定位。常见的室内无线定位技术，如红外、蓝牙、WIFI、超声波、4G等技术，功耗大、信号穿透能力不强、受非视距影响严重，在煤矿巷道的特殊工况环境下应用严重受限。超宽带定位技术(UWB)采用纳秒级的超窄脉冲传输数据，时间分辨率高，超窄脉冲占空比低、功耗低、带宽高、穿透能力和抗干扰能力强，对其他无线通信系统干扰弱，在110 kbit/s低速模式下通信范围可达数百米，非常适合在工况环境恶劣的煤矿井下使用[5-9]。

笔者拟采用低速率UWB技术设计矿井巷道人员与设备精确定位系统，采用基于到达时间差的TDOA算法计算标签到基站的距离，利用卡尔曼滤波对非视距等干扰信号进行滤波，最后采用Chan多基站算法计算标签的三维坐标。

1 UWB定位系统设计

煤矿井下巷道是封闭式的不规则空间，为实现定位信号全覆盖，需要布置多基站，以多基站协同计算实现高精度定位。设计的UWB定位系统结构如图1 所示。

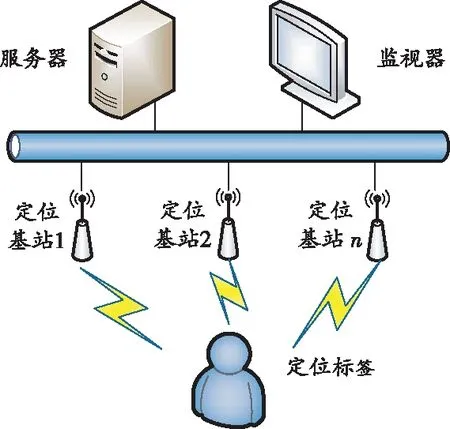
图1 UWB定位系统结构图

定位标签根据自身对位置信息的实时性需求定期向基站发送定位请求，基站收到定位请求后将其发送给服务器，若服务器允许则向收到定位请求的基站及其邻近基站发出对该标签进行定位扫描的命令，基站对标签进行定位扫描后将数据返回至服务器进行计算，得到标签的具体位置[10-11]。

为实现三维定位，标签至少需要处于4个基站的信号覆盖范围之内，且4个基站不在同一平面。巷道基站布置如图2所示。在巷道中每间隔50 m的横截面上布置基站，每个截面上布置2个，且相邻 2个截面的基站一个布置在顶部，另一个布置在对角线上，为减小来自巷道壁的干扰，基站与巷道壁保持0.5 m以上距离。

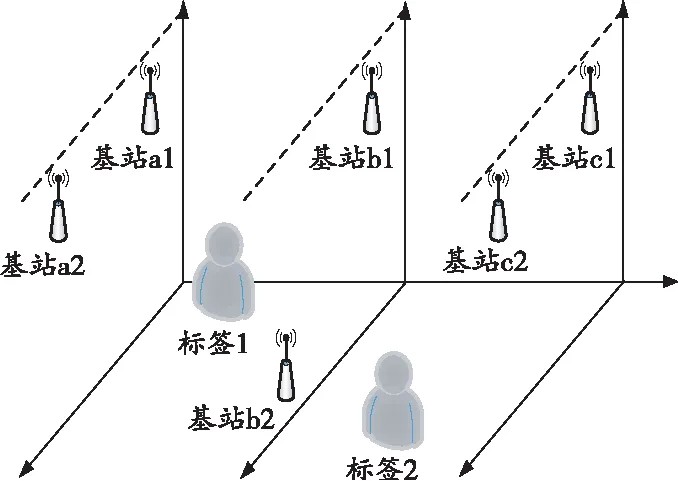
图2 巷道基站布置示意图

2 UWB硬件模块设计

为简化设计，定位基站和定位标签采用相同的UWB模块电路，模块框图如图3所示。

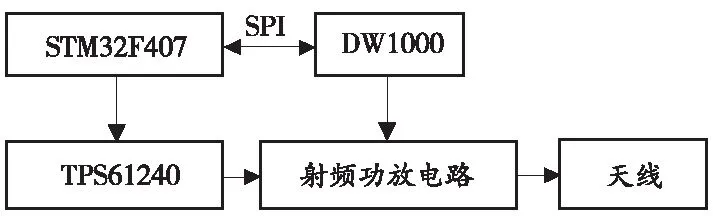
图3 UWB核心模块框图

模块采用Decawave公司的DW1000芯片作为UWB信号处理芯片，其符合IEEE 802.15.4—2011无线标准，采用相干接收技术，并对室内精确定位和通信进行了特别优化，在110 kbit/s传输速率下最远传输距离可达450 m(视距)。为增强抗干扰能力，模块对无线射频信号进行了放大，采用TPS61240芯片为射频功放电路供电，利用三态电源缓冲器SN74LV1T125增强电源电路的抗振能力，提高鲁棒性；为减小整机功耗，只有在定位时，才将TPS61240的EN引脚设为功放电路供电。模块采用全向天线，射频放大电路原理如图4所示。

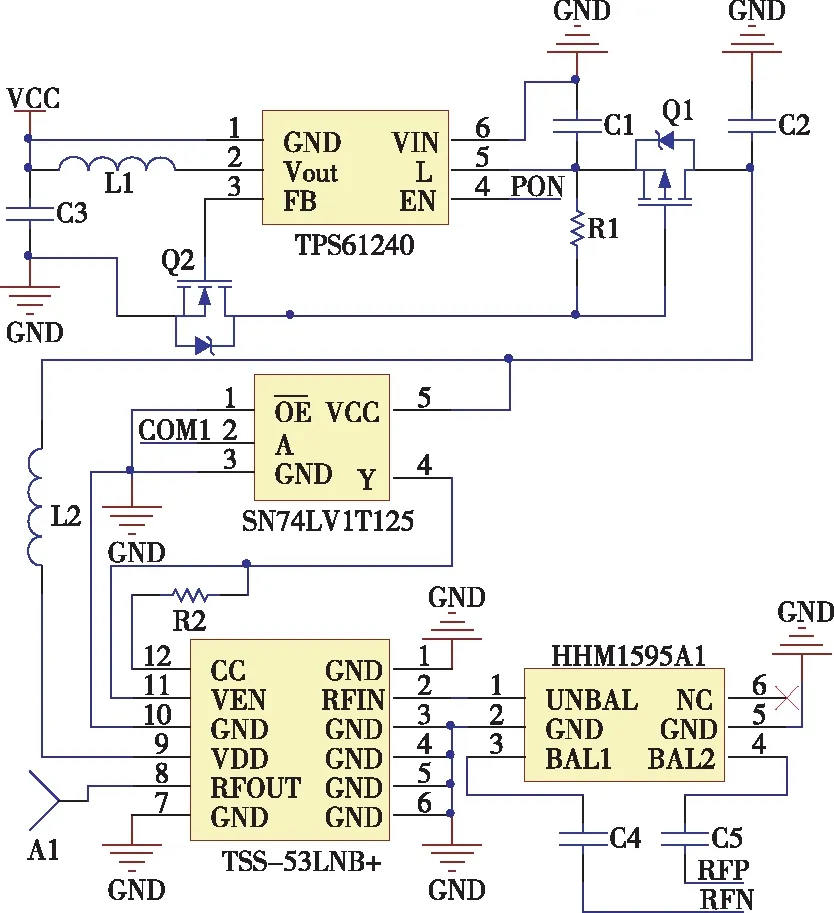
图4 射频放大电路原理图

3 算法设计

定位通常是先采用恰当的方式获得目标到基准的距离，再结合基准的已知坐标计算待测坐标。通常利用信号飞行时间、信号到达角度或者到达信号强度等方法获取距离。鉴于矿井巷道特殊的工况环境，基站布置很难保持统一标准，设备和人员流动性、随意性较强，标签时钟同步困难，笔者采用基站接收信号到达时间差(TDOA)算法计算距离，并对基于到达时间差计算的距离进行卡尔曼滤波处理以减小非视距等干扰，最后结合Chan算法，合理利用多个基站的数据进行三维坐标计算[12-14]。

TDOA三维定位算法可等效为双曲面方程，设标签坐标为LB(x,y,z)，已知基站i的坐标为BS(xi,yi,zi)，则标签到基站i的距离ri为：

(1)

标签到第i个基站与第一个基站的距离差ri1为：

ri1=ri-r1

(2)

ri1=c(ti-t1)=cΔti1

(3)

式中：c为光速；ti为第i个基站接收到信号的时间。

当基站数等于4个的时候，由公式(1)、(2)、(3)便可求得标签坐标。

3.1 卡尔曼滤波

由于矿井巷道空间不规则，人员和设备流动性大，存在严重的非视距误差(NLOS)，实际距离差值可由公式(4)表示:

rn1(tk)=Dn1(tk)+NLOSn1(tk)+w(tk)

(4)

式中：Dn1(tk)为视距下的理论距离差；NLOSn1(tk)是tk时刻的非视距误差，是均值非负的随机变量；w(tk)为系统误差，可以视为高斯白噪声。

为减小NLOSn1(tk)和w(tk)对基站测距带来的误差，对ri1实施卡尔曼滤波处理。将测量值rn1k(k=1，2，…，m)作为观察值，构建系统状态空间模型如下：

(5)

(6)

卡尔曼滤波迭代器由公式(7)～(11)表示：

x(k|k-1)=Ax(k-1|k-1)

(7)

P(k|k-1)=AP(k-1|k-1)AT+Q

(8)

Kg(k)=P(k|k-1)GT(GP(k|k-1)GT+R)-1

(9)

x(k|k)=x(k|k-1)+Kg(k)[Z(k)-Gx(k|k-1)]

(10)

P(k|k)=(I-Kg(k)G)P(k|k-1)

(11)

3.2 Chan算法

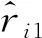
(12)

式(12)中的ei为对应的误差估计，假设ei～N(0,δ2),由式(1)、(2)可得：

(13)

(14)

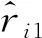
(15)

令：

(16)

(17)

公式(15)可简化为：

φ=H-GP

(18)

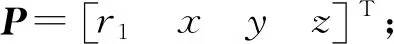
假设r1，x，y，z相互独立，使用加权最小二乘法可得待测向量P的估计：

(19)

实际上，r1与待测坐标(x,y,z)相关，需要对待测坐标进行进一步估计。在干扰条件下：

(20)

误差矢量可表示为：

φ=ΔH-ΔGP

(21)

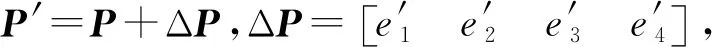
cov(P′)=(GTφ-1G)-1

(22)

(23)

其中:

(24)

φ′的误差协方差矩阵为：

(25)

(26)

最终定位坐标为：

(27)

4 实验及分析

在长280 m、宽5.2 m、高3.8 m的水平走向巷道内按图1、图2所示搭建定位系统。以巷道入口处左下角为原点布置基站，建立坐标系统，采用相位式激光测距仪(精度2 mm)测量定位目标的实际距离。基站通过网口将采集到的标签到达时间上传到模拟服务器进行坐标计算。受限于PCB加工精度与天线安装工艺等，所设计的UWB定位模块在实验巷道内可靠定位距离在160 m以内(丢包率3%以内认为可靠)。实验定位系统内同一个标签同时至少被8个基站搜索到，选取其中6个信号最强的基站数据计算坐标。当标签移动的时候，按照速度方向进行基站切换。分别对固定标签(M1,M2)和沿x轴方向速度不大于1 m/s的手推车移动标签(M3)进行定位，结果如图5～8所示，其中图5和图6分别为安装在不同位置的2个固定标签M1、M2的10次定位结果，图7和图8为移动标签M3在移动过程中每500 ms定位一次的坐标分布图。

图5 M1位置坐标

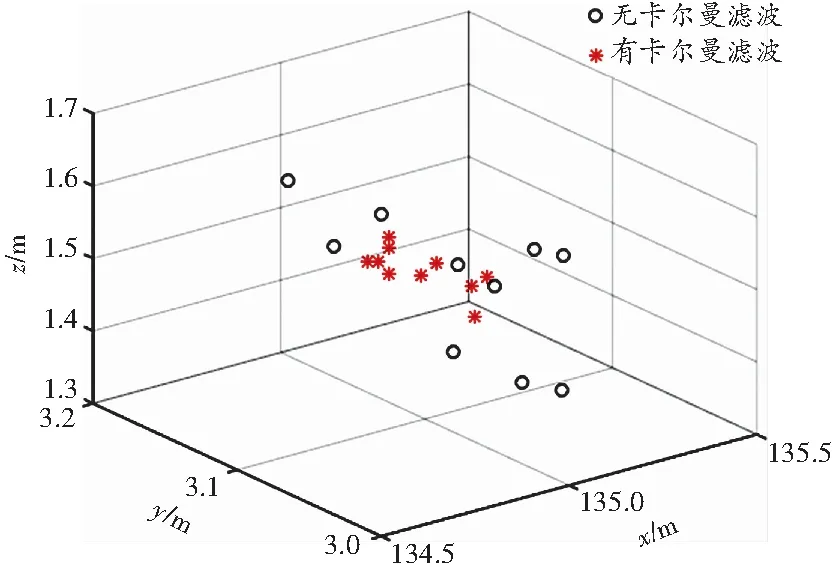
图6 M2位置坐标

图7 M3在x、y轴坐标上的分布

图8 M3 在x、z轴坐标上的分布

对比有无卡尔曼滤波的定位效果，从图5～8可以看出，定位算法中加入卡尔曼滤波得到的位置数据更加收敛，定位精度更高。记第i次测量坐标误差ei为：

(28)

式中：exi、eyi、ezi为第i次测量x、y、z轴方向的误差。用一段时间内的最大误差(EMAX)和均方根误差(ERSME)衡量定位效果，结果如表1所示，其中均方根误差为：

(29)

表1 定位误差

由表1可知，无卡尔曼滤波时，固定标签定位误差最大值达到0.11 m，均方根误差为0.09 m；而加入卡尔曼滤波后，最大误差为0.08 m，均方根误差为0.07 m。移动标签在卡尔曼滤波下最大误差和均方根误差分别为0.09 m和0.08 m。卡尔曼滤波与Chan算法结合与单纯Chan算法相比，固定标签定位精度提高11%，慢速移动标签精度提高27%。