一种散体材料SHPB被动围压试验体应力修正方法*

魏久淇，张春晓，曹少华，王世合，李 磊

（1. 军事科学院国防工程研究院工程防护研究所，河南洛阳471023；2.河南省特种防护材料重点实验室，河南洛阳 471023）

散体介质是一种非平衡态复杂的能量耗散体系，具有优良的削波耗能特性[1]，在地震工程、采矿工程和防护工程领域受到广泛应用，如砂土常作为防护结构分配层的填充材料。该类工程在地震、爆炸冲击等强荷载作用下的响应与材料在高应变率下的动态力学特性密切相关。分离式霍普金森压杆（SHPB）是研究材料中高应变率力学特性的常用设备，散体材料往往需要厚壁圆筒和垫块控制材料的初始条件，从而实现该材料的SHPB被动围压试验，国内外诸多学者[2-16]利用该方法对砂土等散体材料的动态力学特性开展了大量研究。SHPB被动围压试验中，试样及厚壁圆筒内部的应力场和应变场很难通过现有的技术直接测量，目前得到材料体应力-应变关系的主要手段是将厚壁圆筒的受力状态简化为平面应力问题[17]，测量厚壁圆筒外表面（如图1所示）的环向应变εc，由下式计算得到，

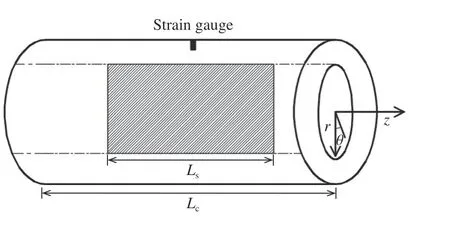
图1 散体材料受约束的几何结构Fig.1 Geometric structure constrained by SHPB test for bulk material

式中：σrr为极坐标下径向应力； εrr为极坐标下的径向应变；εzz为轴向应变；Ec、νc分别为厚壁圆筒的弹性模量和泊松比，εc为应变片测到的厚壁圆筒环向应变，a为厚壁圆筒的外径与内径的比；p为体应力，εV为体应变。

对于固体材料而言，因不存在装样困难，在满足SHPB均匀性假定的条件下，试样的初始厚度可以做到与厚壁圆筒长度等长，在小应变范围内，材料的体应力应变利用式（1）～（4）计算并无不妥；当试样厚度与厚壁圆筒不等长时，根据Forquin 等[18]分析厚壁圆筒会发生不均匀凸出变形，图2样厚度较长时，试验时厚壁圆筒的几何变形图。由圣维南原理易知，厚壁圆筒L段受力状态仍可以看成平面应力问题，式（1）～（4）仍有效。然而由于散体材料波阻抗远小于压杆的波阻抗，试样厚度很小才能满足SHPB均匀性假定条件，加之受装样限制，试样厚度远小于厚壁圆筒的长度，此时端部效应可能会覆盖整个不均匀凸出区，公式（1）～（4）的有效性需要予以探讨。以往研究石英砂的动态力学特性时，大多只分析砂子的轴向应力应变，Luo等[11]没有考虑端部效应的影响直接引用式（1）～（4）计算砂子的体应力-应变关系，这有失严谨。魏久淇等[5]和文祝等[6]认为由式（1）计算的材料径向应力与真实应力存在折算系数关系，但并未给出合理的验证。Bragov 等[15]注意到了该问题，并设计了一个阶梯型的圆筒（如图3所示），装样时将试样置于厚壁对应位置，该方法可以极大限度弱化端部效应，计算材料体应力应变时可直接引用式（1）～（4）。然而该方法存在两个弊端：一是圆筒薄壁越薄，端部效应对试验结果的影响越小，但圆筒加工难度越大；二是试验时无法改变试样的初始厚度。

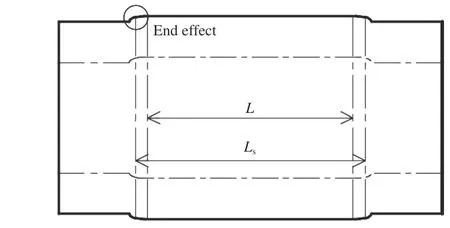
图2 试验时厚壁圆筒的几何变形图Fig.2 Geometric deformation diagram of thick-walled cylinder in test

图3 阶梯型套筒[15]Fig.3 Ladder sleeve[15]

本文中，不改变厚壁圆筒结构，使用传统厚壁圆筒固定装样的方法，利用Autodyn 软件分析了试样实时厚度对材料真实体应力应变的影响，基于厚壁圆筒理论提出一种修正方法，并对非饱和钙质砂进行准一维应变冲击试验和数值仿真，验证修正方法的可靠性，以期对开展散体材料SHPB被动围压进行指导。

1 有限元分析

Autodyn 可用于分析气体、液体和固体及它们之间耦合作用的高速、瞬态动力学的问题，本文用该软件辅助分析特殊工况下（试样厚度远小于厚壁圆筒长度），式（1）～（4）的有效性，并给出科学计算材料体应力应变的思路。

1.1 建立模型

假定试样为准一维应变状态，图4为试样应力均匀时厚壁圆筒的受力示意图，此模型忽略了试样与厚壁圆筒内壁摩擦力。由图4可知，当试样应力均匀时，厚壁圆筒内壁承受沿材样实时厚度Ls均布径向内推力σss，根据连续性条件可知 σss=σrr，由式（1）可知εc=2σrr/[Ec(α2-1)]。利用Autodyn 建立厚壁圆筒模型，对厚壁圆筒内壁试样实时厚度Ls区施加给定σss(t)，输出厚壁圆筒外中点环向应变εs，对比εs和εc，若εs=εc，则说明式（1）～（4）有效，若 εs≠εc，则反之。图5为建好的厚壁圆筒模型，选用朗格朗日算法，厚壁圆筒为自由边界条件。

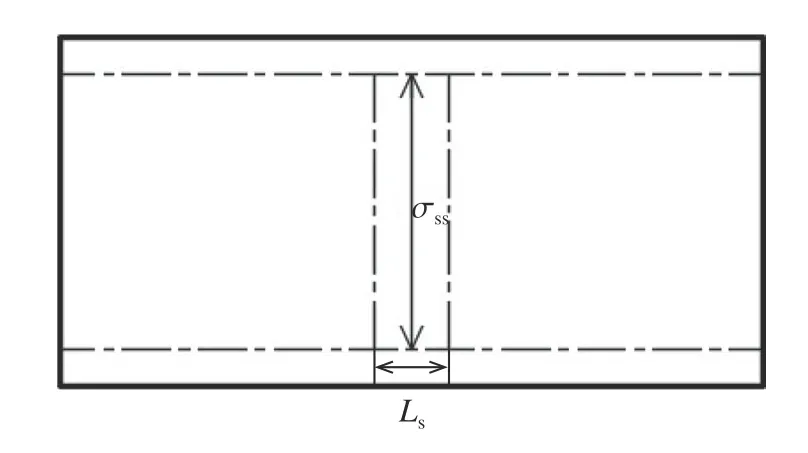
图4 厚壁圆筒受力分析Fig.4 Force analysis of thick-walled cylinder

图5 厚壁圆筒模型Fig.5 Thick-walled cylinder model

1.2 结果与分析

图6为给定的σss时程曲线，由图6可知 σss为动态力，可以真实模拟试验时厚壁圆筒受到的动态径向内推力。

对于不同的Lc和Ls，图7给出了公式值εc和数值计算值εs(Lc,Ls) 对比图，其中Lc与Ls的单位为mm。公式值εc为σss带入式(1)计算出的厚壁圆筒外表面的环向应变。由图7 可知，当试样实时厚度大于30 mm，式(1)有效，当试样厚度小于20 mm 时，式（1）无效。研究发现：当砂样实时厚度小于20 mm，公式值εc与数值计算值εs(Lc,Ls) 存在折算关系：k=εc/εs(Lc,Ls)，k为折算系数，试样实时厚度仅影响折算系数的大小。

图6 径向力σ ss时程曲线Fig.6 Time-history curve of radial force σss

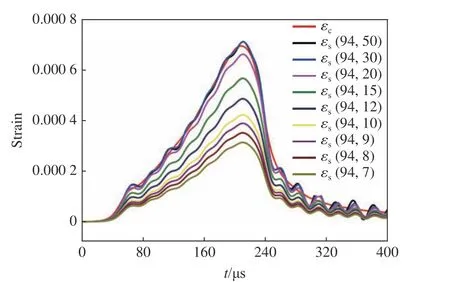
图7 应变公式值（εc）与数值计算值（εs(L c, L s)）的对比Fig.7 Comparison diagram between strain by fomula (εc)and that by simulation (εs(L c, L s))

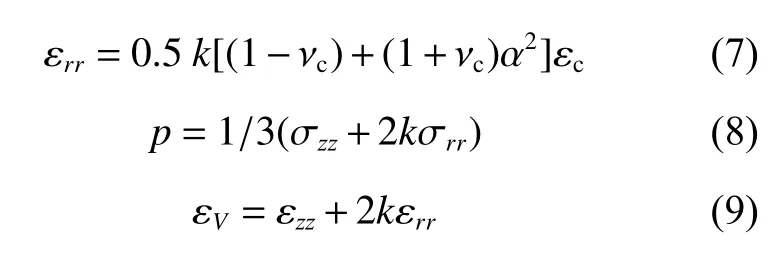
1.3 有限元仿真验证

为了验证上述仿真方法的可靠性，本文开展了数值模拟，图9为试样实时厚度与厚壁圆筒等长（Ls=Lc）时，本文模拟计算值εs(Lc,Ls)与εc的（式(1)理论值）对比图。由图9可知，当试样实时厚度与厚壁圆筒相等时，仿真计算值与理论值吻合较好，因此本文Autodyn 有限元分析方法具有一定的可信度。

2 试验验证

为进一步验证本文方法的可靠性，本文开展了含水率为25%和30%非饱和钙质砂SHPB被动围压高速冲击试验，每种含水率重复3次试验。含水率为25%和30%非饱和钙质砂受高速冲击压缩可转变为饱和钙质砂。水在饱和钙质砂中对应力应变关系起主导作用，由于水的等向性，理论上饱和钙质砂的轴向应力等于径向应力。非饱和钙质砂受高速冲击压缩转变为饱和钙质砂时，若式(6)计算的径向应力和轴向应力相等，则能进一步验证本文方法的可靠性。

图8 折算系数与试样实时厚度的关系图Fig.8 relation diagram between conversion coefficient and real-time thickness of samples

图9 验证性模拟Fig.9 Verification simulation

2.1 材料基本参数和工况

本文所用材料为钙质砂，图10为钙质砂试样，呈乳白色，主要成分为CaCO3，掺杂有少量红色颗粒（碳酸镁）。原始砂样经过24 h 充分烘干后，经标准筛筛分称重后的级配曲线见图11，考虑到试样直径及试样厚度，大颗粒的存在无法满足试样均匀性，极小颗粒量少不易称量，故将砂样中粒径小于0.15 mm 和大于1.18 mm 的粒径剔除，剔除后剩余粒径的砂样组分不变，钙质砂的比重为2.82，最大最小干密度分别为1.378和1.183 g/cm3，实际工况如表1所示。

图10 试验砂样Fig.10 Sand specimens tested

图11 砂样颗粒级配曲线Fig.11 Grain size distribution

表1 试验工况表Table 1 Summary of SHPB tests

2.2 试验设备

本文所用SHPB 试验装置为直径37 mm 的铝杆，如图12(a)所示。子弹长度、入射杆以及透射杆分别为400 mm、2 000 mm 和2 000 mm。由于钙质砂为松散介质，为精确控制试样的初始条件，试验时用厚壁圆筒和垫块束缚成试件。垫块和厚壁圆筒如图12(b)、图12(c)所示。厚壁圆筒材质为4340钢，弹性模量为210 GPa,泊松比为0.3，内径37.1 mm，外径为47 mm，长为94 mm；垫块材质跟压杆材质完全相同，直径为37 mm，厚度为30 mm。

2.3 结果与分析

试样装样步骤参考Song 等[2]研究成果，整形器为厚1 mm 直径10 mm 橡胶片。图13是试验时的原始典型波形。砂样动态应力平衡是评判试验数据有效的重要方法，图14为钙质砂试样的动态应力平衡图，由图可知试样基本满足应力平衡条件。

图12 试验设备Fig.12 Test equipment

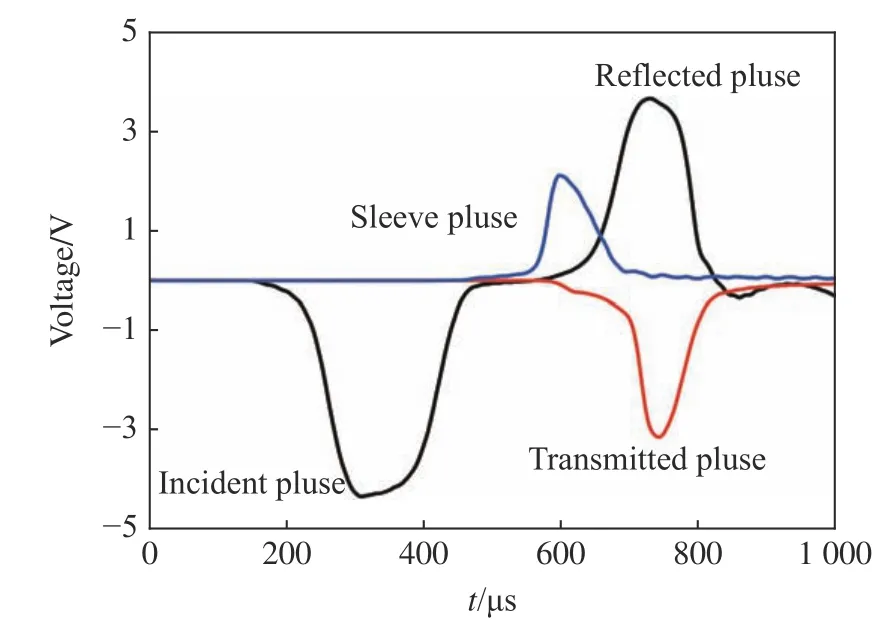
图13 试验原始波形Fig.13 Test the original waveform

图14 砂样动态应力平衡Fig.14 Dynamic stress equilibrium in the sand specimens

图15为含水率25%、30%钙质砂的应力-应变曲线。厚壁圆筒的屈服强度为835 MPa,由拉梅公式[19]易知厚壁圆筒内应力（等于砂子的径向应力）大于325 MPa 时，厚壁圆筒才会屈服。由图14可知钙质砂的最大轴向应力为102 MPa，易知厚壁处于弹性状态。本文砂样的轴向应变为10-1量级，由式（5）～（7）易知径向应变为10-4量级，故钙质砂可以看成准一维应变状态。因此可得，

式中：e为孔隙比，wsat为饱和含水率，Gs为骨架密度。由式（10）、（11）和（12）易得含水率25%和30%非饱和钙质砂受高速冲击压缩转变为饱和时的应变拐点，分别记为Sr1、Sr2（见图15）。由图14可知：钙质砂含水率越高，受冲击压缩更易饱和，达到饱和点后，由于水不可压缩，其应力-应变曲线迅速趋陡峭。图14中钙质砂的径向力σrr是由式（5）～（6）计算得到的，由图可知，饱和状态时，钙质砂的轴向应力和修正过的径向应力基本相等，这主要是因为水在饱和钙质砂中起主导作用，水对四周力相等。综上可知，本文方法具有可靠性。

图15 含水率25%、30%钙质砂的应力应变Fig.15 Stress and strain of calcareous sand with 25%,30%water content

3 结论

本文利用有限元分析给出了一种解决办法，并用数值仿真和试验两种方法验证本文方法的可靠性，主要得出以下结论。

（1）散体材料SHPB被动围压试验时，试样厚度远小于厚壁圆筒长度时，由于端部效应导致厚壁圆筒不均匀凸出变形，求解材料的体应力-应变关系时不能将厚壁圆筒应力状态简化为平面应力问题。

（2）厚壁圆筒处于弹性状态下，通过厚壁圆筒理论计算出的材料径向力与材料真实径向力存在一定比例关系，在一定范围内，折算系数与试样实时厚度存在二次函数关系。

（3）试样厚度、厚壁圆筒长度、厚壁圆筒内外径之比以及厚壁圆筒材料特性都会影响折算系数，各因素之间还存在多种耦合关系，解析解也尚未给出，仍需进一步探讨。开展类似试验时，针对具体情况，可利用本文提供的方法分析折算系数。