基于Gabor变换和加权欧式距离FCM的CT图像分割算法设计与实现

赵 娟，袁慧宇①

（1.淮北师范大学 计算机科学与技术学院，安徽 淮北235000；2.淮北师范大学 信息学院，安徽 淮北235000）

0 引言

近年来随着医学影像仪器的发展，医学影像发挥的作用越来越大，尤其是核磁共振、CT（Computed Tomography，电子计算机断层扫描）等，是医生诊断病人疾病的重要依据［1］. 从大量影像数据中分割出有助于医疗诊断的图像是医学影像数据处理的重要步骤，而分割质量往往受限于医生的经验和状态，分割质量良莠不齐. 通过程序批量分割影像数据已成为当前医学影像处理的重要趋势［2-3］.

FCM（Fuzzy C-Means，模糊C均值）是一种聚类算法，专家们发现将该算法应用于图像分割中可取得较好的效果［4-6］. 但在实际应用中，往往容易受到噪声的干扰. 人们提出一些改进的FCM算法，如基于密度加权［7］，基于贝叶斯局部空间信息［8］，基于局部模糊信息［9］，基于生物地理学［10］，基于极值距离［11］和MRF-FCM［12］等算法通过改进聚类距离度量提高分割效果. 此外也可通过提取图像特征作为分类依据，从而降低噪声影响，如文献［13］使用小波变换提取图像特征，利用该特征代替原始像素点灰度作为后续分割依据，进一步降低噪声的影响. 文献［14］提出一种基于超像素的快速FCM图像分割算法，能完成快速准确分割彩色图像，但需预先指定分类数. 文献［15］利用小波变换消除图像噪声，取得一定的效果，但算法复杂度较高. 文献［16］使用双树复小波变换，通过锐化图像边缘提高分割质量. 文献［17］使用Ga⁃bor和Frangi滤波器来增强血管图像，再使用FCM分割，结果表明平均准确度达到0.961. 本文使用Gabor变换提取图像特征建立特征向量，提出加权FCM 算法，通过优化特征向量的权值，获得更好的分割结果.

1 算法介绍

1.1 Gabor变换

Gabor变换是在傅里叶变换基础上增加高斯窗，从而获得图像局部信息. 通过改变窗口中心可获得图像各部位特征信息，具有良好的方向选择性和尺度选择性，效果与哺乳动物视觉细胞滤波响应类似，在提取图像的边缘特性及局部特征具有良好的效果. 二维Gabor函数定义为：

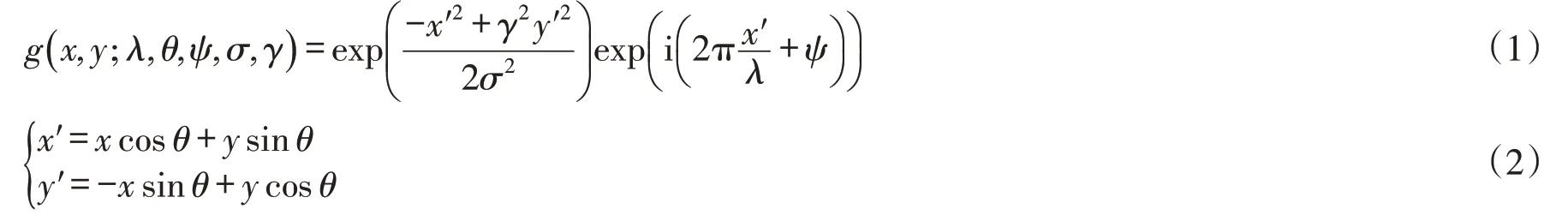
式中，x和y为像素坐标，λ为滤波波长，θ为Gabor核函数角度，ψ为相位偏移量，σ为高斯函数尺寸，γ表示长宽比.

对每个Gabor 核函数g(x,y;λ,θ,ψ,σ,γ )，可以通过计算图像P 与Gabor 函数卷积获得图像P 的Gabor滤波，图像上点P0(x0,y0)相应的图像特征Oφ,l( z0)表示如式（3）所示.

其中，*为卷积，则对于该Gabor滤波器可以获得图像P特征集合S={Oλ,θ,ψ,σ,γ(x0,y0)}. 对于每个像素点则可构成不同Gabor滤波器提取的特征向量，用于进一步分割.

1.2 FCM分类

FCM算法在图像中选取c个点作为初始聚类中心，计算图像像素点与初始聚类中心点的相似度获得其所属聚类的隶属度，然后通过拉格朗日迭代算法确定像素点最优划分. 在这里选取聚类目标函数J为

该式约束条件如下

其中隶属度uij表示点j属于聚类中心vi的隶属度，m为模糊隶属度矩阵模糊度，‖xj-vi‖表示像素点j到聚类中心i的相似度，通常采用欧氏距离计算. 但常规欧式距离未考虑不同Gabor滤波器所得特征在分割时重要程度，某些参数下Gabor滤波器提取的结果更能体现图片的特征，本文提出一种加权欧式距离计算公式.

式中δλσθγ∈［0，2］为Gabor滤波器特征对应权值，该值越小则相应特征值在计算距离时的重要程度越高，当δ=1时，则式（6）退化为常规欧式距离，通过优化δ可获得最佳分割结果，如何优化δ是一个难点，需要根据具体图像分割结果进行优化.

对于式（4）进一步利用拉格朗日算法迭代uij得到最优聚类中心和各像素点隶属度，迭代公式如下：

当迭代前后uij和vi的变化量均小于阈值时停止迭代，获得最终分类.

1.3 GWFCM算法及优化

基于以上讨论，提出基于Gabor变换的加权FCM图像分割算法（简称GWFCM）总体流程如图1所示，步骤如下.

（1）首先初始化Gabor 滤波器集合，并提取训练图片CT 图像特征，根据特征值的清晰程度选择合适的滤波器，获得特征值集合S.

（2）选取初始聚类中心. 为避免随机聚类中心对分割结果的影响，本文采用密度法［18-19］选取初始聚类中心.

（3）采用有监督的网格搜索算法对权值δλσθγ进行优化，搜索范围为［0.5，1.5］，搜索步长为0.1，分割结果参考CCIR500-1 五级评价质量系统［20］进行评估.

（4）获得优化后的Gabor滤波器和对应权值.

其中步骤（1）中Gabor滤波的作用为过滤噪声和无用信息，保留对分割有利的细节信息；步骤（3）中δ的优化作用是增加重要滤波信息在分割中所占权重，提高分割准确度. 基于以上算法流程，可获得优化后的Ga⁃bor滤波器和欧式距离权值δ，该结果可以应用于同类CT照片分割. 为验证所得结果适用性，对测试CT 图分割，并与同类算法比较，试验过程如下.

图1 分类优化算法

2 实验

使用python 基于numpy、cv2、pillow 和sklearn 等函数库实现所提出算法. 首先初始化Gabor 滤波器，滤波器参数选取范围如下：γ∈[0.2,1.1] ，λ ∈[4,12] ，σ ∈[4,12] ，θ∈[0,2π)，步长分别为0.3，2，2和π/4. 为说明各参数对滤波器形状及滤波效果的影响，列举部分滤波器如图2所示，图下方的说明给出参数变化时取值，参数默认值如下：γ=0.5，λ=10，σ=10，θ=0.

图2 Gabor滤波器参数对滤波器的影响

用图2滤波器对某脑部CT图像（训练图）进行Gabor变换，结果如图3所示.

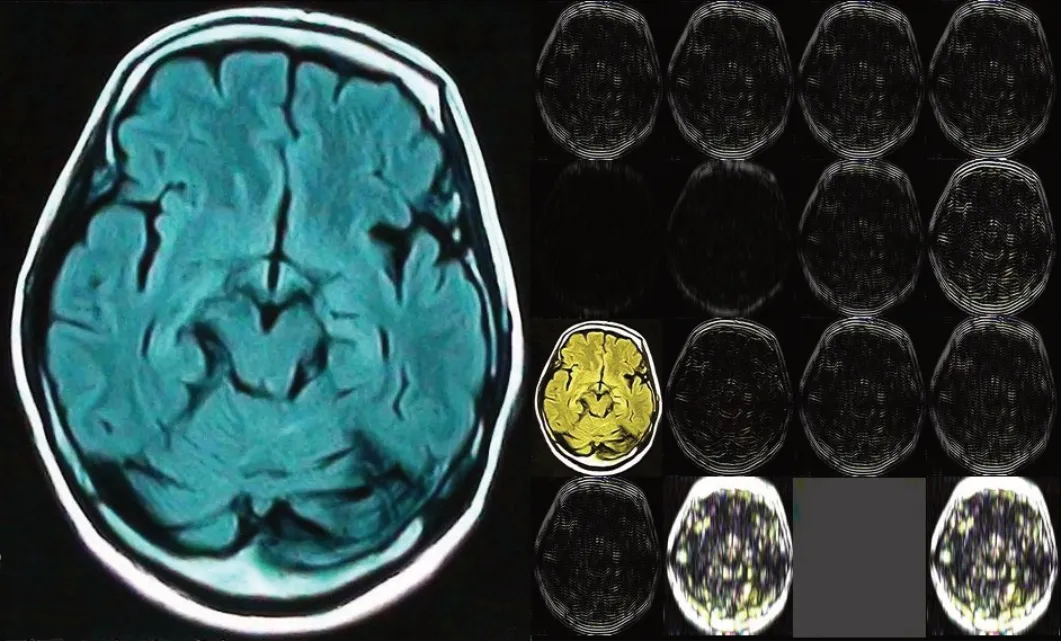
图3 脑部CT及变换结果

图3左侧为原始脑部CT 训练图，右侧16张为变换结果，排列顺序同图2. 发现γ的变化并不影响滤波结果，如图3 右侧第一行图片所示，4 张图片并无差别. 这是因为滤波结果仅受到滤波器频率特性影响，而长宽比γ对滤波器频率特性影响可以忽略［21］，所以将γ从待优化列表中移除，令γ=0.5. 而λ、σ和θ的变化对滤波效果影响很大，如图2（b）第1、2个滤波器的波长过小，滤波结果集中于高频部分，丢失大量的低频特性，不利于进一步分割；2（c）第1个滤波器σ设置过小，保留全部纹理，缺乏特征信息；图2（d）第3个滤波器所得结果缺乏任何信息，表明训练图在该滤波方向下未提取到特征，在优化时放弃该方向滤波器.

根据所得特征清晰程度，从中选择6个滤波器. 基于密度法在原始训练图片选取3个聚类中心，基于式（6）～（8）进行分割. 因分割结果最终用于医学诊断依据，本文以降低噪声，分割边缘清晰为优化目标，参考CCIR500-1 五级评价质量系统［20］，采用有监督的网格搜索算法进一步优化权值δλσθ，取值范围δλσθ∈［0.5，1.5］. 为加快搜索进度，采用歩进法调节网格大小，初始网格设为0.3，获得初步优化结果后，再减少网格至0.1 进一步搜索优化. 为比较分割效果，基于FCM、PCM（Possibilistic C-Means 可能性c均值）和GWFCM算法对图像分割，结果如图4所示.

图4 训练图像及分割结果

图4（a）为原始训练图像，图4（b）FCM分割结果受到噪声影响比较严重，图像中间出现较多噪点，而且分割边缘也不清晰；图4（c）PCM分割结果噪点较少，但分割边缘同样不清晰；图4（d）GWFCM所得结果噪点更少，而且边缘更加清晰. 为进一步验证本文算法，同样用FCM、PCM和GWFCM算法对3张CT图片进行分割，所得结果如图5所示.

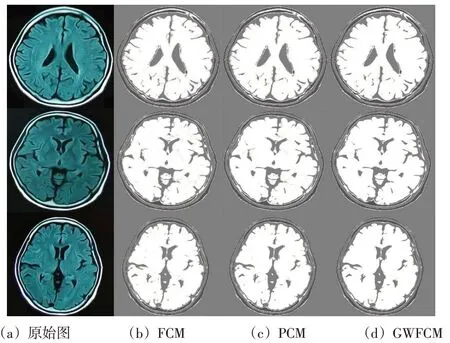
图5 测试图像及分割结果

图5左侧是原始图，右侧3列为3种算法分割结果. 与图4类似，FCM所得结果边缘部分较为粗糙，噪声较多；PCM 所得结果噪声相对较少，但边缘也较为粗糙；GWFCM 所得结果噪声最少，边缘更加清晰.说明由于训练图片与测试图片非常类似，所以在训练图片上优化后的滤波器和权值同样适用于测试图片，证明本文的算法有效性.

3 总结

为实现医学CT图像的批量准确分割，本文提出一种基于Gabor变换和加权欧式距离的GWFCM图像分割算法. 利用Gabor变换提取CT图像特征，筛选出合适的特征值组成图像特征向量. 基于该特征向量使用加权欧式距离FCM 进行分类，并使用有监督的网格搜索法优化权值. 结果表明对于训练图片和测试图片，GWFCM分割结果均优于FCM和PCM算法分割结果，表现在噪声更少，边缘更加清晰，证明本文所提GWFCM图像分割算法针对医学CT图像分割的有效性.