SVM模型在河流年径流量预测中的应用

摘要：介绍了SVM的基本原理，指出了其在解决样本非线性问题中表现的特有优势，并将SVM和BP神经网络在叶尔羌河年径流量预测结果进行了对比。结果表明SVM方法预测精度要略优于BP神经网络方法。

关键词：径流量预测;神经网络;SVM模型;叶尔羌河

前言

水文系统中影响预测对象的因子众多，影响因子与预测对象之间关系复杂，目前较多地用显式的统计模型进行预测。但是统计模型缺乏自适应性，更新困难，具有不确定性，拟合历史资料的精度较高，而预测检验的精度却时好时坏，不是十分稳定。许多事实己经说明，水文系统中很多变量间的复杂非线性关系远非简单的代数方程所能有效表达。

近年来，支持向量机（Support Vector Machines，简称SVM）的研究在各个领域广泛开展。SVM是Vapnik等根据统计学习理论（Statistical Learning Theory，简称SLT）提出的一种新的机器学习方法，在解决小样本、非线性问题中表现出许多特有的优势，并在模式识别、函数逼近和概率密度估计等方面取得了良好的效果。本文采用SVM模型对叶尔羌河多年径流量进行年径流量预测，旨在为国内相关研究提供参考。

1 SVM模型基本原理

SVM方法是从线性可分情况下的最优分类面（Optimal Hyper Plane）提出的。假设d维空间中线性判别函数的一般形式为，分类面方程为

对判别函数进行归一化，使两类样本都满足≥1，即使离分类面最近的样本的=1，这样分类间隔就等于，因此间隔最大等价于使（或）最小。而要求分类线对所有样本正确分类，就是要求其满足

式中：ai为拉格朗日乘子;c为常数;为可调的权重向量;为松驰变量。

最优分类面问题可以表示成如下的约束优化问题，即在式（2）的约束下，求函数

的最小值。这是一个二次规划问题，可定义以下的拉格朗日函数：

求式（3）的极小值就是对w和b求拉氏函数的极小值。求L对W和b的偏微分，并令其等于0，可转化为如下的对偶问题。

2 应用实例

2.1 建模方式

（1）样本归一化处理。归一化处理有利于避免各个因子之间的量级差异，消除量纲和单位不同对各个因子的影响，因此应对样本的输入、输出参数进行（0，1）归一化处理。

（2）确定核函数。由于核函数对算法的影响较大，因此选择一个最好的核函数极为重要。这里以径向基函数作为SVM方法中的核函数，建立推理试验模型。

（3）核参数的选择。采用Cross-validation方法便可得到核的参数。

2.2 模型参数的确定

选取叶尔羌河卡群水文站的年径流量实测资料（1958～2015年）作为研究对象，其中1958～2010年的数据作为训练数据，2011～2015年的数据作为检验数据。在预报建模中假设未来值和过去值存在某种确定的函数关系，利用过去的观测值估计未来值：

式中：q（t）为当前时段径流量;q（t-n）为n个时段前径流量。

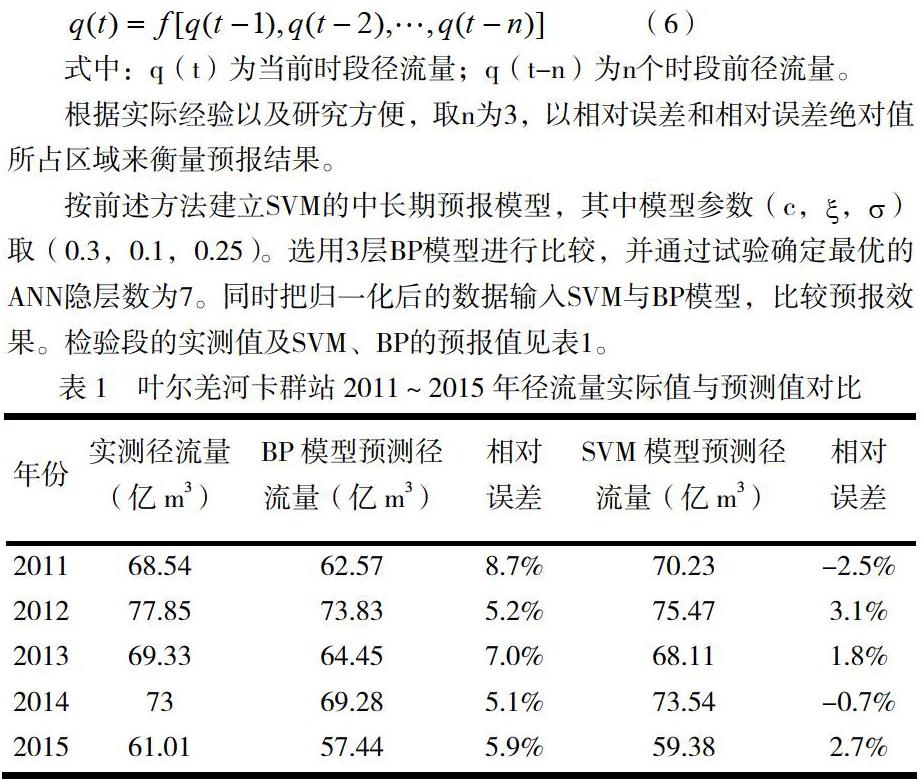
根据实际经验以及研究方便，取n为3，以相对误差和相对误差绝对值所占区域来衡量预报结果。

按前述方法建立SVM的中长期预报模型，其中模型参数（c，，）取（0.3，0.1，0.25）。选用3层BP模型进行比较，并通过试验确定最优的ANN隐层数为7。同时把归一化后的数据输入SVM与BP模型，比较预报效果。检验段的实测值及SVM、BP的预报值见表1。

从表1可以看出：在预测阶段，SVM模型要比BP模型效果要好，平均相对误差分别为0.9%和6.4%，说明支持向量机用于径流量预测比BP神经网络有更高的精度和鲁棒性，是可行的。

3 結论

SVM是一种基于SRM的小样本学习方法，克服了BP网络结构难以确定和不易达到全局最优的缺陷。SVM算法将问题转化为二次优化问题，得到的解是全局最优解;而用BP网络进行预测得到的解可能是局部最优解。因此，SVM预测方案解决了BP网络方法中无法避免的局部极值问题，在精度上优于BP网络预测方案。

参考文献：

[1]陈永义，俞小鼎，高学浩，等.处理非线性分类和回归问题的一种新方法（I）——支持向量机方法简介[J].应用气象学报，2004，15（3）：351-352.

[2]冯汉中，陈永义.支持向量机回归方法在实时业务预报中的应用[J].气象，2005，31（1）：41-44.

[3]黄奕铭.支持向量机在雷雨天气预报中的应用[J].广东气象，2006，28（1）：22-24.

[4]张伟，何新林，刘兵.SVM在玛纳斯河流域径流预测中的应用与研究[J].人民黄河，2008，30（5）：35-36.

作者简介：杨磊（1986- ）男，新疆库尔勒人，大学本科，主要从事水利工程及水政水资源管理工作。