交织区多车道协同自适应控制方法*

2020-12-29马庆禄袁新新

交通信息与安全 2020年4期

马庆禄袁新新张琳

（重庆交通大学交通运输学院重庆400074）

0 引言

交织区是道路系统的重要组成部分，尤其山地城市受地形、地物等客观条件的限制，多条匝道并入主线形成多路合流交织区，极易引发交通事故。虽然分车道控制配合定向车道对这类交织区的安全性有了很大的提升，但研究发现在高峰期多路合流交织区的交通延误现象更为严峻[1]。因此，优化多路合流交织区控制方法对降低交织区的车辆延误具有重要的意义。

现阶段，对交织区的控制方法的研究主要包括自适应控制方法和分车道控制方法。其中自适应控制方法的研究主要包括匝道控制、可变限速控制，以及匝道和主线协同优化控制。对匝道控制方面的研究有需求-容量控制[2]、可接受间隙控制[3]、ALINEA控制[4]，以及刘丽琴等[5]借鉴RWS-C 控制策略，研究影响快速路合流区通行能力的匝道控制方法。近几年学者对可变限速控制做了大量的研究[6-8]。Liu等[9]以燃油损耗最小为目标，建立了可变限速控制模型FC-VSL。杨晓芳等[10]研究在车车通信环境下的车辆经过合流影响区的运行情况，并提出车辆速度控制模型。Park 等[11]在车车通信环境下，通过改进智能驱动变道咨询算法，控制主路车提前变道让行匝道车辆并通过Vissim 仿真验证了其算法的有效性；对匝道和主线协同优化控制的研究方面，Zhang等[12]在保证通行效率的前提下提出了一种主线可变限速和匝道控制相协调的控制系统。周浩等[13]通过实际交通流数据，利用可变限速与匝道协同控制，有效的改善快速路交通流状态。在分车道控制方法方面的研究，安旭等[14]在NS 元胞自动机模型的基础上，建立针对交织区3种换道规则的元胞自动机模型来探究交织区不同车道分配方案对系统产生的影响效果。陈亮等[15]基于元胞自动机的多车道交织区离散模型，仿真模拟饱和状态下多车道交织区交通流演变过程,分析交织区拥堵的形成机制。薛行健等[16]研究有无车道平衡设计对交通流运行所产生的影响，并探讨了现有车道平衡设计存在的局限及对策。马新露等[17]建立了城市道路多路合流的元胞自动机模型，结果表明不同形式的变速车道对各合流车道产生不同的影响。李璨等[18]以交通冲突率为目标，提出车道单元组合最佳优化方案。刘伟等[19]以合流车道通行能力最大化为目标，建立合流车道最优组合方案，使得交织区的实际通行能力得到很大提升。

综合现有的研究成果，交织区控制方法在快速路或高速路的主路与单条匝道的合流路段的自适应控制和不同形式车道组合的研究较多，多路合流交织区的主线与匝道、匝道与匝道的分车道自适应控制的研究罕见。基于此，考虑多路合流交织区车辆运行特征，提出一种分车道自适应协同优化控制方法，通过对不同车道交通流数据的实时感知，以及各种限制因素和约束条件，动态驱动交织区信号配时，得到不同控制方案。以最小总延误为目标得到最优控制方案。最后，利用Vissim仿真平台，对以上方法进行了验证，从而使控制效果得到优化。

1 多路合流交织区自适应控制

自适应控制的原则是通过感知交通数据，合理的改变各车道的相位相序和自适应信号配时来减少交织区的延误，保证交织区内车辆高效通行，从而避免各个车道发生溢流。主要包括:数据实时感知和分车道自适应控制，其中分车道自适应控制又分为进口车道相位相序优化、自适应配时、最小总延误3 个模块。进行自适应协同控制时，具体的控制流程见图1，当检测到各车道的交通流量和排队长度发生变化，根据各车道的约束条件重新组合相位相序，得到不同的分车道控制方案。再根据自适应相位绿时和信号周期，动态调整各方案的信号配时，最终得到最优的组合方案。当检测到放行的各车道相位相序不变时，根据各车道的交通量和排队长度判断是否进行信号配时，是否得到最小延误，否则返回车辆检测。

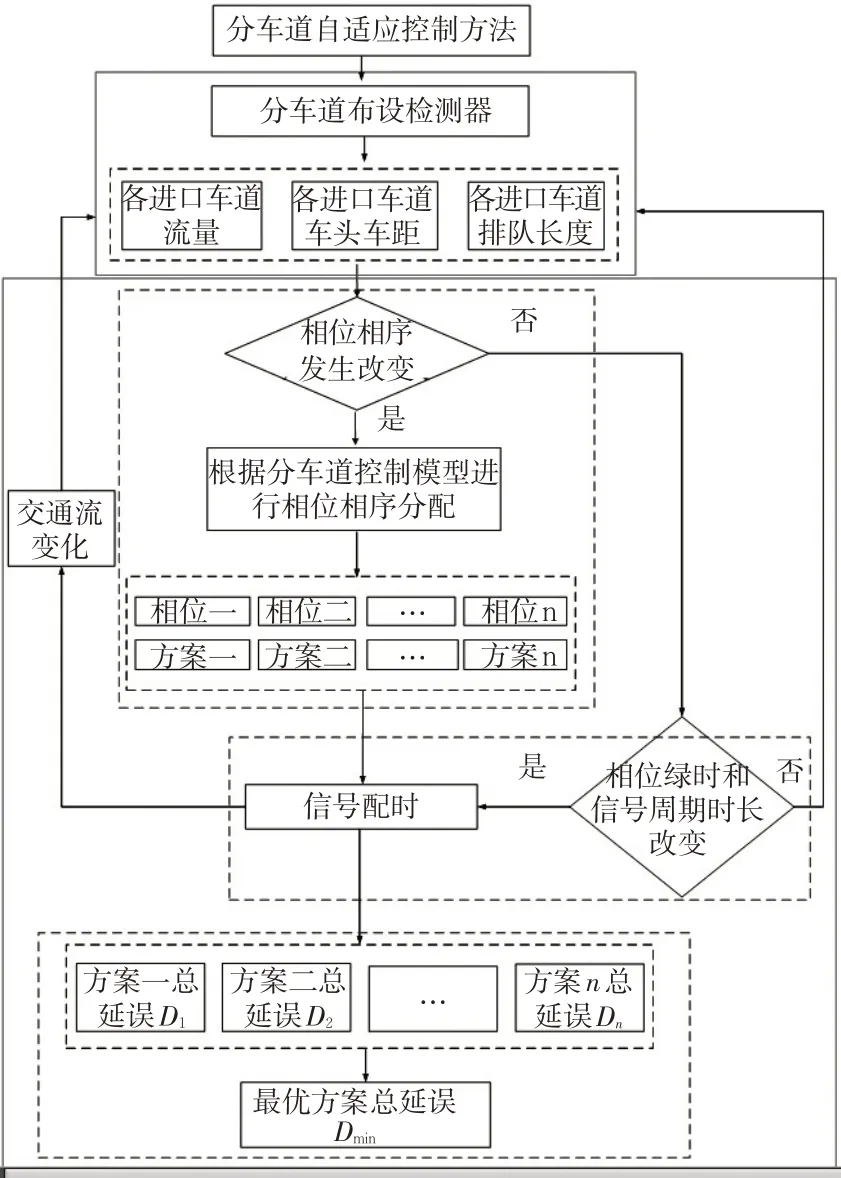
图1 自适应控制具体流程Fig. 1 Adaptive control specific process

2 多路合流交织区说明

2.1 多路合流交织区结构特征

多路合流交织区主要表现为多个进口的车辆在较短的距离内合流，图2 为山地城市主干道系统中常见的3路合流交织区。

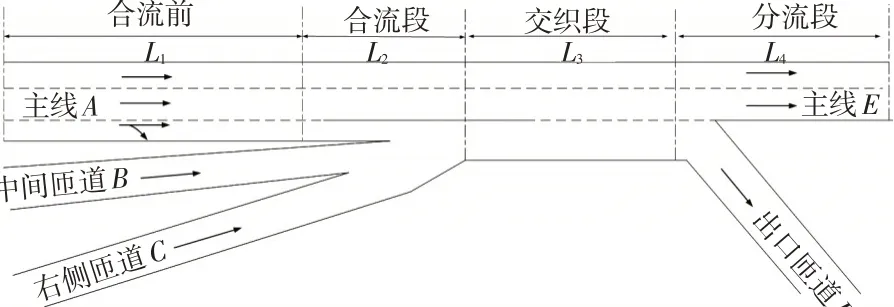
图2 多路合流交织区示意图Fig. 2 Schematic diagram of multi-channel merging weaving section

由图2可见，2股匝道（中间匝道B、右侧匝道C）同时连接1条主线（主线A），在有限的交织长度内变换车道，分流出去。中间匝道B 和右侧匝道C 来向的车辆到主线出口E 会靠近合流区变道，主线A 和中间匝道B 车辆到出口匝道D 会靠近分流区变道，整个交织区入口车道数大于出口车道数，车流紊乱，交织复杂，严重影响道路的通行效率。

2.2 多路合流交织区数据采集

进行分车道自适应控制时首先需要获取实时交通流数据。在数据采集中，对渠化后的交织区使用检测器感知交通流数据，交织区各进口车道检测器布设情况见图3。

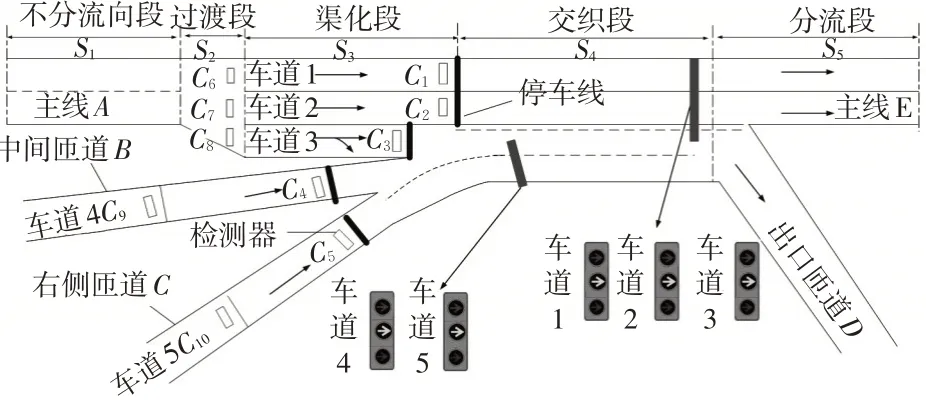
图3 进口道检测器布设Fig. 3 Imported lane detector layout

由图3可知，5个进口车道共布设4组检测器，第1 组包括C1～C3号检测器，布设在停车线位置，第2组包括C6～C8号检测器，布设在进口道过渡段，第3组包括C4、C5号检测器，布设在停车线位置，第4组包括C9、C10号检测器，布设在实际的最大排队长度处，通过以上各车道检测器的布设，可感知各个车道的交通量、车头时距、排队长度等。

3 自适应协同控制模型

3.1 多路合流交织区各车道复杂度

多路合流交织区的进口车道数越多，交织越复杂，形成的冲突点也越多[20]。根据多路合流交织区的入口车道数大于出口车道数，以图3 为例，nA，nB，nC为交织区各进口道，nD，nE为交织区各出口道，结合定向车道渠化，建立各车道复杂度模型，表达式为

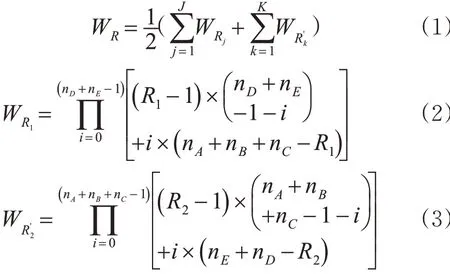
式中:WR为第R 条车道复杂度的计算值；WRj为渠化后的交织区第R 条车道中第j 条进口车道所有流向交叉点数的乘积；WR'k为渠化后的交织区第R 条车道车辆经第k 条出口车道的所有流向上的交叉点数的乘积；R 为交织区段的第R 条车道（由最外侧车道数起），R = 1,2,…,N ，N 为交织区区段的车道总数；R1，R2分别是与R 同一侧车道数起的交织区进口第R1条车道、出口的R2条车道；J 为进入第R 条车道的进口车道的数量；K 为驶离交织区段的第R 条车道的出口车道的数量。

渠化后的交织区各车道的复杂度用概率表示为

式中pN为第N 条车道基于冲突概率的相对复杂度。

3.2 相位相序优化模型

考虑到多路合流交织区存在多种车流方向，交织区内不同车流方向集合可表示为T ={ }T1,T2,…,Tn，共有n 个车流方向。为了全面考虑不同信号相位控制方案下车道复杂度对交织区的影响，采用m × n 维变量矩阵P 表示1个周期的相位组合方案

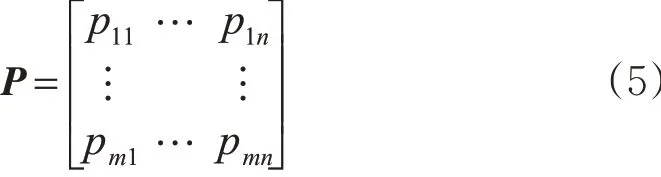
式中:i = 1,2,…,m; j = 1,2,…,n ；矩阵的元素pij为在第i 个相位中第j 条车道通行状态，pij= 0 表示红灯状态，pij= 1表示绿灯通行状态。

由于多路合流交织区进口道数与出口道数不均衡、各进口车道间具有不同程度的影响，为了保证多路合流交织区内车辆的安全高效通行，需要对控制方案的合理性进行约束。结合矩阵变量P 构建分车道控制相位相序约束条件。

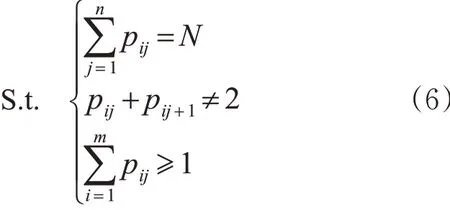
式中: i ∈(1 ,m ); j ∈(1 ,n )。相位矩阵P 可以表达所有的相位组合，i 为交织区相位的数目，j 为车道流向。式（6）中第1 个约束条件表示放行的车道数和交织区内的车道数相匹配；第2 个约束条件表示交织区各车道复杂度较大的车道，不可同时放行；第3个约束条件表示各车道至少放行1次。

3.3 自适应信号配时

自适应信号配时是在不同的相位相序方案下，根据多路合流交织区的交通状况，对周期、饱和度、排队长度约束，确定信号配时，使交织区总延误最小。各车道通过在放行时间内驶出的交通量以及红灯开始时的排队长度得到下1个周期的平均交通量。

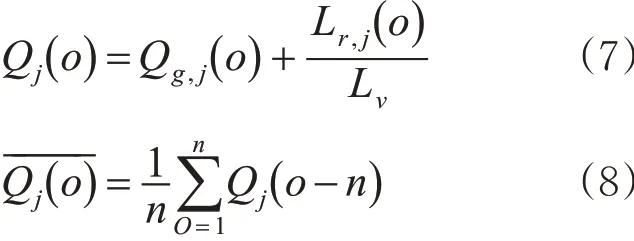
根据实时感知数据，计算各车道车流连续通过时的平均车头时距。

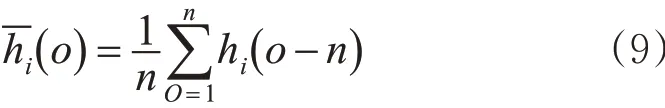
为了避免多路合流交织区发生拥堵，需要约束每个相位饱和度和车辆排队长度在合理的范围内，以保证交织区的通行能力，约束条件见式（10）。

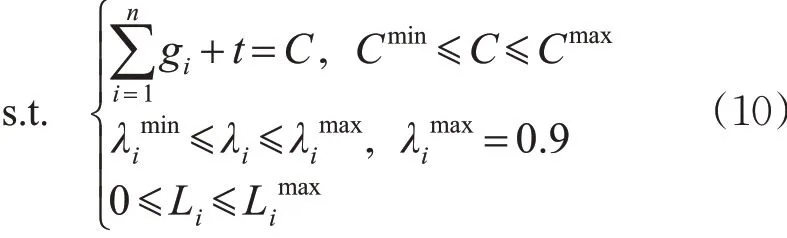
式中:Cmin，Cmax分别为最小和最大的信号周期；C为各相位的有效绿灯时间gi加上清空时间t 等于周期时长；分别为i 相位的最小饱和度、i 相位的饱和度、最大的饱和度，为了保证多路合流交织区的通行能力最大，λimax取0.9；Li为i 相位的排队长度；Limax为多路合流交织区i 相位的实际最大排队长度。

根据以上数据便可求得各进口车道所需绿灯时长。

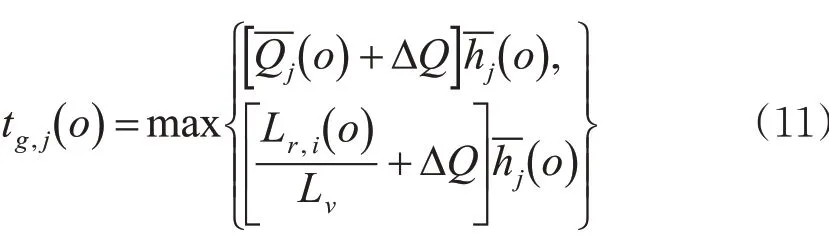
3.4 总延误优化模型

根据Webster 模型，不同车流方向每辆车的平均延误，表达式为

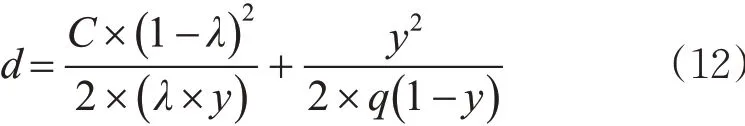
式中:q 为车流量；C 为信号周期；λ 为绿信比，y 为各放行车道的饱和度。

根据相位相序约束条件得到的不同控制方案以及交织区不同车流方向的延误，得到基于总延误的分车道控制优化模型，表达式为

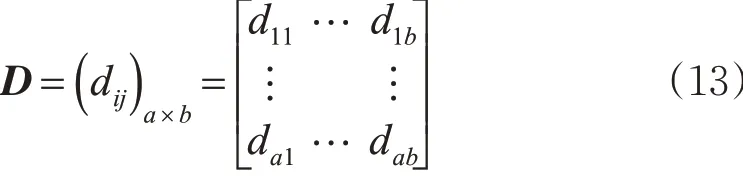
式（13）中，矩阵D 为交织区分车道控制共有a 种方案，b 种车流方向；dij为第i 个分车道控制方案在j方向产生的平均延误。控制方案为i 时，所有车流方向的延误值。交织区的运行效率应保证总延误最小，最小总延误模型为

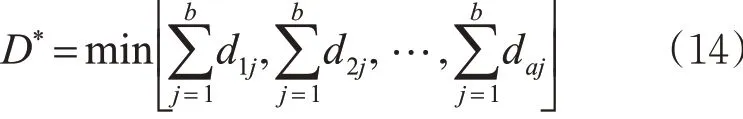
式中:D*在控制方案为i 时，交织区各个车流方向总延误最小，此时的控制方案达到最优的效果，为最佳方案。

4 实例仿真

4.1 交织区现状

在2019 年9 月10 日对重庆市渝中区黄花园与石黄隧道交织区（见图4）进行调查。

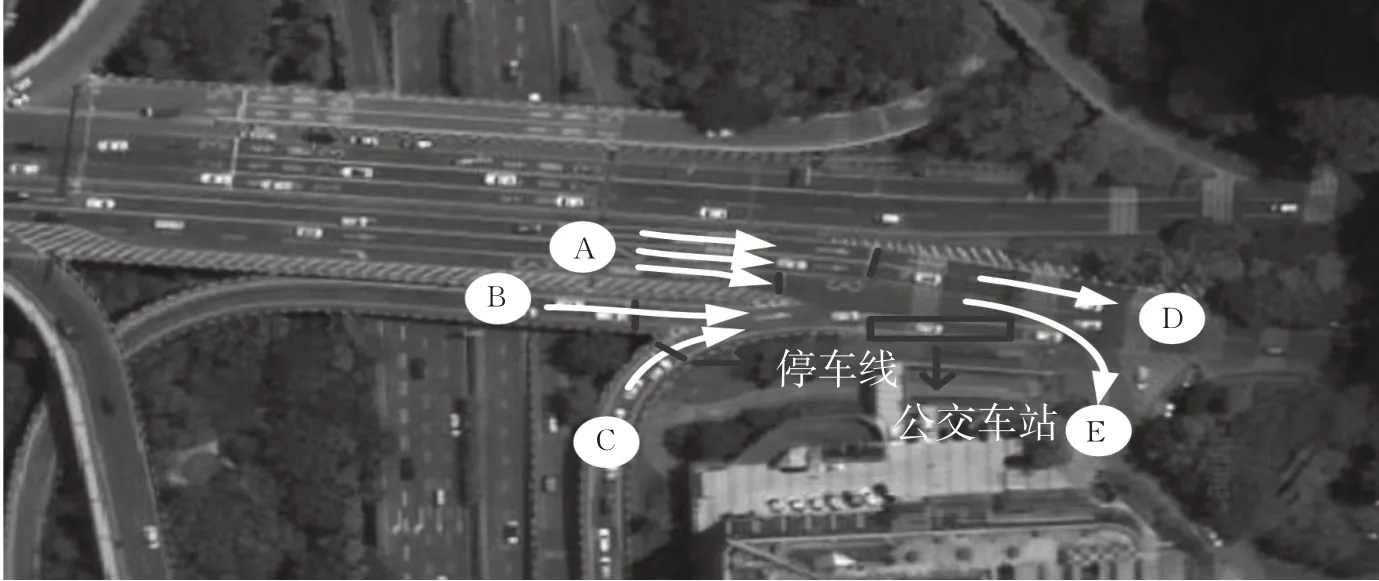
图4 黄花园与石黄隧道交织区渠化示意图Fig. 4 Diagram of channelization of weaving section between Huanghua Garden and Shihuang Tunnel

由图4 可知，黄花园大桥与石黄隧道交织区包括A，B，C，D，E共5个进出口，江北方向入口为3车道，临江门、大溪沟方向入口均为1车道，3方向交织区域处设置有公交站，分别是来自江北方向、大溪沟方向的公交车。各车道车辆通过信号控制在100 m左右的合流路段上自主择道、完成交织后，小部分车流驶入双钢路，而相当大部分车流汇入2 车道的黄石隧道。由于交织区域内有公交车站，小汽车延误明显增加，分车道信号控制不能满足各进口道车辆，造成很大的延误。该交织区采用分车道4 相位控制，相位1 的有效绿灯时间30 s,相位2 的有效绿灯时间为22 s，相位3 有效绿灯时间为15 s，相位4 有效绿灯时间为20 s。高峰小时各进口道汇入流量与流向见表1。

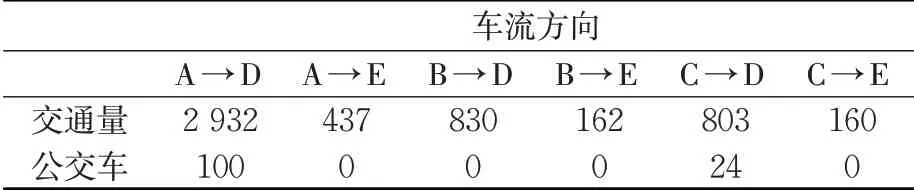
表1 高峰小时交织区汇入流量与流向（08:30—09:30）Tab. 1 Peak-hour interleaving inflow and flow direction（08:30—09:30）pcu/h

根据式（5），在现状4 相位控制条件下，即i = 4时，不同相位不同车道的信号灯状态pij可以表示p11= 1,p12= 1,…,p45= 0 ，那么现有分车道固定控制方式可以用矩阵P 形式表示为

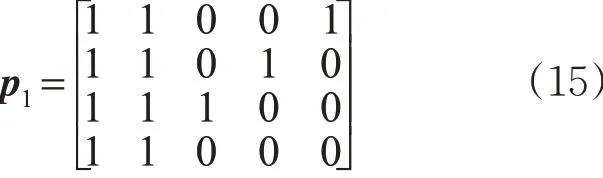
4.2 不同控制模式与仿真结果分析

根据表1 调查的高峰小时交通量，图3 所示的交织区渠化，进行仿真参数设置，设主线速度为60 km/h，上、下匝道最大速度为50 km/h，公交车速度为30 km/h，各个车道上设置检测器，信号控制方案包括相位相序、绿灯时间。即Vissim 中建立仿真运行环境，见图5。

图5 交织区仿真图Fig. 5 interleaved zone simulation diagram

由于多车道交织区的复杂性，1个相位应至少有3个车道的车辆具有通行权。在式（4）中得到车道4和车道5 复杂度相对较高，即pi4+ pi5≠2 i ∈(1,N) ，在式（6）中定义j = 5 , N = 4 ，共有19种控制方案。当n = 2 时，2相位控制方案下有7种控制方案，用p2si表示；当相位数n = 3 时，3相位控制方案下有12种控制方案，用p3si表示。根据2相位和3相位不同的控制方案动态调整信号配时，并通过Vissim 软件得到不同控制方案下各车流方向的延误情况，见表2和表3。

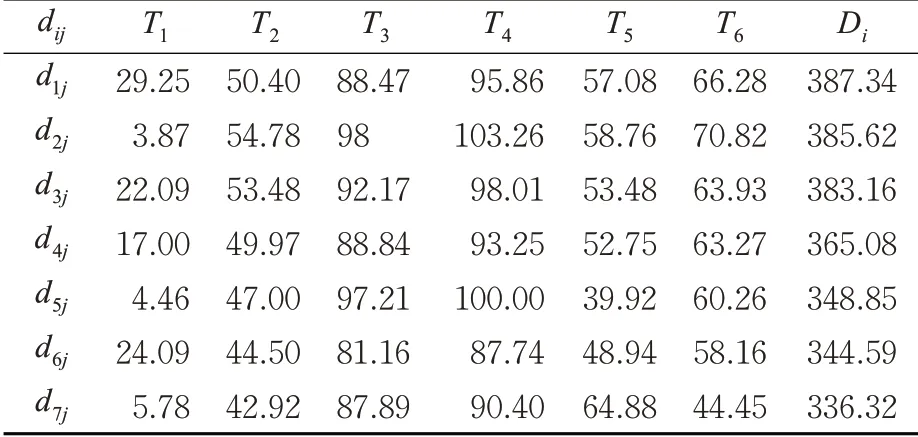
表2 2相位组合方案下各方向的延误Tab. 2 Delays in all directions under the two-phase combination scheme s

在表2 中，T1，T2，… ，Tn( n = 6 )分别表示A →D ，A →E ，B →D ，B →E ，C →D ，C →E方向。由式（13）和式（14）得交织区不同方案不同方向的总延误Di，此时i =(1 ,2,…,7) 。从表2 可以看出，第1 种控制方案（P2S1）各个方向的总延误最大，达到387.34 s，第7 种控制方案（P2S7）各个方向的总延误为336.32 s。相比较2相位控制方案，高峰小时交通量下第7 种控制方案是最佳控制方案，各个方向的总延误最小，相比分车道固定控制下的延误，方案7总延误降低了26%，提高了交织区的运行效率。2相位方案7（P2S7）用矩阵P 形式表示为

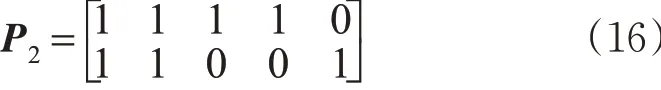
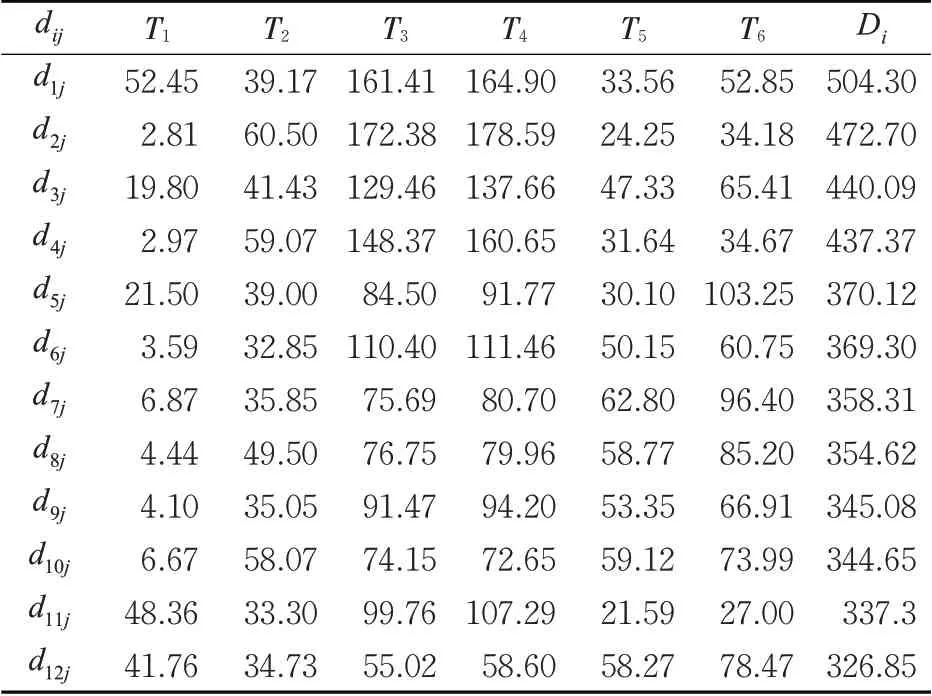
表3 3相位组合方案下各方向的延误Tab. 3 Delays in all directions under the three-phase combination scheme s

由表3 可知，3 相位控制方案i 的取值为i =(1 ,2,3,…,12 )，其中方案1（P3S1）各个方向的总延误504.30 s，总延误最大，方案12（P3S12）各个方向的总延误为326.85 s，总延误最小。比较3 相位12种控制方案，在高峰小时交通量下第12种控制方案是最佳控制方案。延误相对分车道固定控制降低了27%。3相位方案12（P3S12）用矩阵P 形式表示为

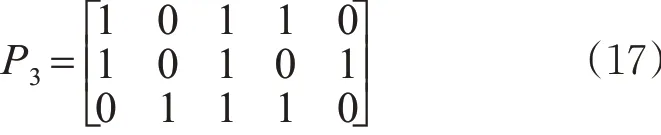
为了更好的比较2 相位和3 相位控制方案中哪个是最佳控制方案，对现状控制（P）、2 相位方案7（P2S7）和3相位方案12（P3S12）进行效果对比，见图6。

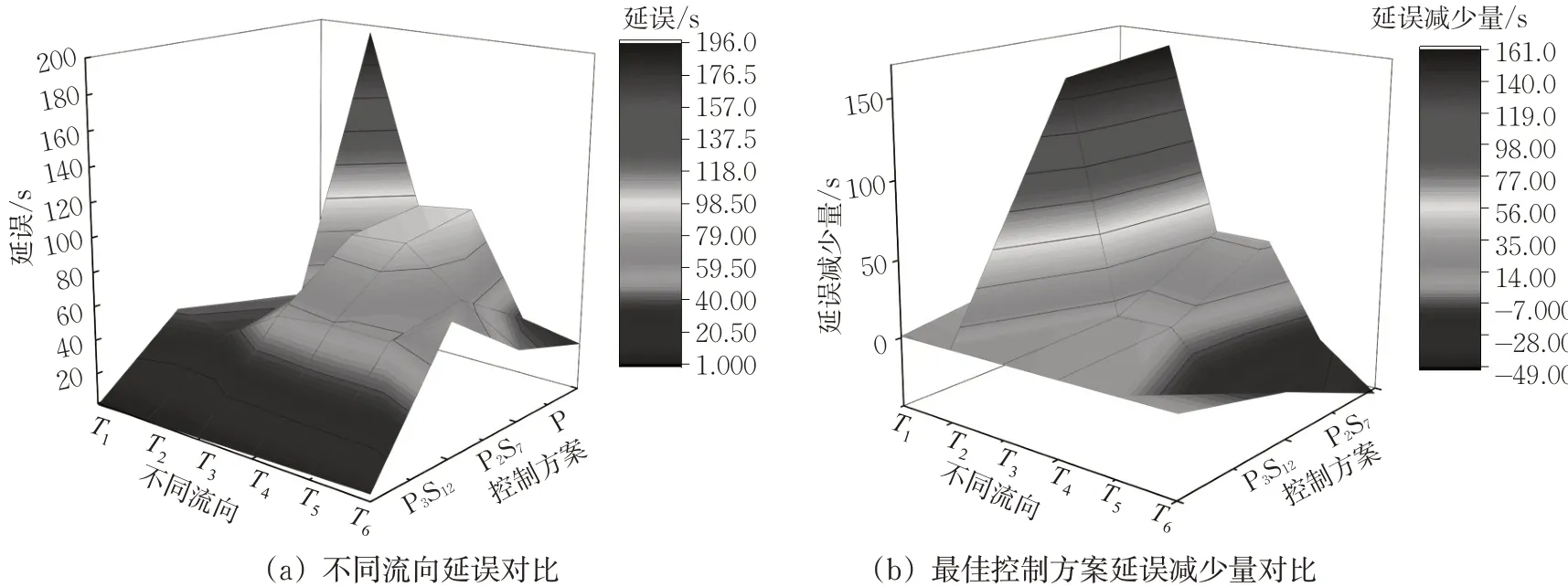
图6 现状控制、2相位方案7和3相位方案12效果对比Fig. 6 Status control，two-phase plan 7 and three-phase plan 12 effect comparison

从图6（a）可以看出，现状控制、2 相位方案7、3相位方案12不同流向的延误波动范围依次降低，且整体服务等级依次为E 级、D 级、D 级。3 相位方案12 各方向平均延误起伏较均匀。从图6（b）可以看出，3相位方案12各方向的延误减少量明显高于2相位方案7。通过对比分析高峰小时交通量下不同控制方案各方向延误、总延误以及服务等级，可以看出3 相位方案12 是高峰小时交通量最优控制方案，总延误最小，不同方向的延误较均匀，服务等级由E级优化为D 级，运行效率最佳。当交织区交通量变化时，仿真不同时段流量状态下，分车道固定控制下的延误与分车道自适应协同控制下的延误，得到车辆总延误效果见图7。

由图7（a）可知，延误随车流量变化而变化，当车流量较少时，分车道固定控制下交织区车辆延误波动在200 s左右，当车流量较大时，分车道固定控制下交织区延误在400 s 左右。由图7（b）可知，延误随车流量变化而变化，当车流量较少时，自适应协同控制下的交织区车辆延误波动范围小于100 s，当车流量较大时，自适应协同控制下交织区车流量延误小于300 s。为了更好的比较不同时段流量状态下交织区分车道固定控制与动态分车道自适应协同控制总延误优化效果，对不同时段分车道固定控制与动态分车道自适应协同控制延误减少量和延误降低率对比分析，见表4。

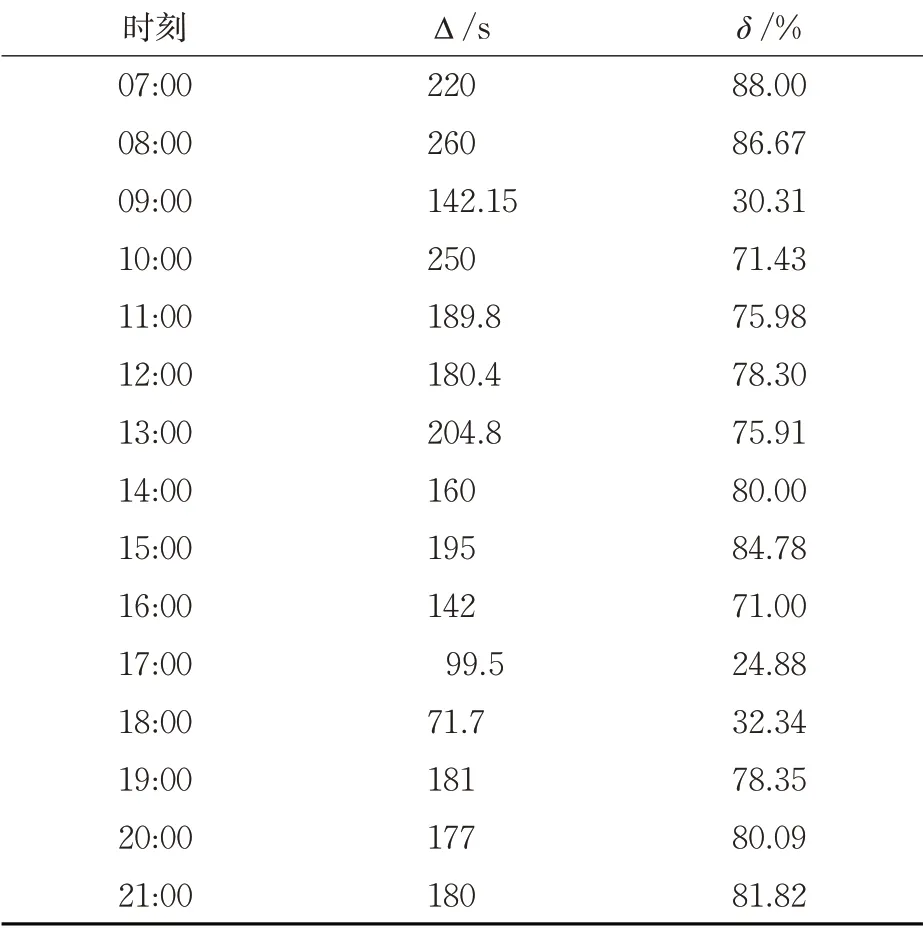
表4 总延误优化数据分析Tab. 4 Total delay optimization data analysis

由表4 可知，不同时段内分车道固定控制延误与动态分车道自适应协同控制延误减少量均为正值，由于黄花园大桥—石黄隧道交织区高峰时段为早高峰08:00—09:00、晚高峰17:00—18:00，分车道自适应控制高峰时段延误降低率在24%～32%，平峰时段降低率为71%～88%。7:00 到21:00 延误平均减少量为176.89 s，平均降低率为69%，分车道自适应协同控制效果显著，明显提高了道路的通行效率。