考虑过分相区的高速铁路列车操纵节能优化*

樊 葱 柏 赟 周雨鹤 汪 茜 文 晶

（北京交通大学综合交通运输大数据应用技术交通运输行业重点实验室 北京100044）

0 引 言

由于牵引能耗增长导致总运营成本增加，高速铁路牵引节能问题日益受到关注。优化列车操纵方案可以在几乎不增加投资的前提下降低高速列车牵引能耗，是一种经济可行的方法。

高速列车操纵与牵引、制动特性及线路条件有关。由于阻力和牵引力的非线性特征，列车操纵节能优化是典型的非线性最优控制问题。该类问题相对复杂，通常使用启发式算法和数值方法求解[1]。其中，启发式算法所得解仅为较优解，无法在理论上证明其最优性，数值方法可以求得最优解，包括间接法、动态规划和直接法[2]。

B.K.Ichikawa[3]首先采用基于极大值原理的间接法搜索以节能为目标的列车最优控制策略。I.P.Milory[4]指出最优操纵策略包括牵引、惰行、制动3个阶段。P.Howlett[5]发现平直道路上的节能方案为依次采用最大牵引、巡航、惰行和最大制动，这种方法被称为“标准四阶段法”。SCG研究所的学者们[6-8]对不同运行条件下列车最优操纵问题进行研究并证明最优解的存在。针对高速铁路列车，刘建强等[9]、王青元等[10]使用间接法证明并求解得到最优节能操纵方案。

动态规划和直接法较间接法计算效率更高，也被广泛用于求解列车节能操纵方案。直接法分为控制参数化方法和控制-状态参数化方法。Wang Y.等[11]和仲维锋等[12]的研究分别说明动态规划和控制参数化方法在线路长度较短的小规模案例上能取得较好结果。但动态规划和控制参数化方法的计算时间极易受变量维度和约束条件数量影响，不适宜求解区间线路长且约束复杂的高速铁路列车节能操纵问题，否则计算时间将显著增加。

控制-状态参数化方法中的伪谱法能够有效处理各种约束，通过离散状态变量避免了数值积分过程，计算速度较快[13]。伪谱法最初多应用于航空领域，解决飞行器轨迹优化等问题[14]。Wang Y.等[11]首次将高斯伪谱法应用于求解列车节能操纵方案，并与动态规划等算法的优化结果进行对比，证明了伪谱法能较快求得优化效果最好的解。Wang P.等[15]考虑信号系统约束，使用高斯伪谱法求解运行调整后的列车最优控制问题，也能在较短时间内得到较好的优化结果。

尽管既有研究在模型快速求解方面取得了一定突破，但现有文献中的模型对于实际约束考虑不全面，如很少考虑列车过分相区的影响，而高速列车在分相区内必须断电惰行。麻存瑞等[16]基于标准四阶段法考虑列车在分相区惰行的要求，采用遗传算法求解定时节能操纵问题。虽然标准四阶段法在一般情况下具有较好的节能效果，但其在巡航阶段保持最大允许速度运行，不一定最适用于考虑分相区惰行的列车节能操纵。因此，有必要对考虑列车在分相区惰行的节能操纵方法进行优化。

本文以高速铁路列车牵引能耗最小为优化目标，建立考虑列车过分相区、曲线限速等实际约束的多阶段最优控制模型，使用GPOPS II(General Pseudospectral Optimal Control Software Version 5.0，以下简称“GPOPS”)求解，验证求解列车节能操纵方案时考虑过分相区约束的必要性和本文模型的优化效果。

1 考虑过分相区的列车最优控制问题

1.1 高速列车多阶段节能控制优化问题

高速列车最优控制问题可以描述为在线路、运行时间等已知的前提下[17]，从一类满足约束的列车操纵方案中找出1个使列车从起点运行到终点过程中牵引能耗最小的方案。列车操纵方案通常包括牵引、巡航、惰行、制动工况，仅牵引、巡航工况可能使用牵引力从而产生牵引能耗。由于不同的操纵方案中各工况的使用情况不同，因此其所需能耗不同，在所有方案中必然存在1种使得列车牵引能耗最小的方案。

由于列车在站间运行的可选操纵方案数量众多，为了缩小可行解的规模以提高求解效率，本文以水平位移s 作为自变量, 将运行区间划分为多个阶段。本文根据限速、坡道和分相区将区间划分为R个阶段，各阶段的限速、坡道唯一，见图1。

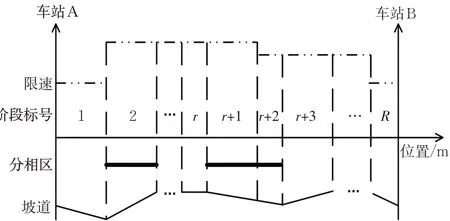
图1 区间阶段划分示意图Fig. 1 Phase division of a railway section

在任一阶段r，除自变量水平位移s外，表征列车运行状态的变量还有速度v 和时间t，记作状态变量x(r)(s)=[x(r)1(s),x(r)2(s)]T=[v(r)(s),t(r)(s)]T。列车运行状态变化的根本原因是列车通过输出不同的牵引力F或制动力B改变受力情况，所以以F、B为控制变量，记作u(r)(s)=[u(r)1(s),u(r)2(s)]T=[F(r)(s),B(r)(s)]T。

1.2 高速铁路分相区

高速列车运行过程中须采用惰行工况通过分相区。分相区是高速铁路接触网上用于隔绝不同相位的区域。隔绝不同相位的原因是电力系统采用3相交流电，而列车运行仅需要单相电，但如果仅从3相电网中的某一相取电，容易造成各相负荷失衡[18]。为解决这一问题，接触网上每隔一段距离就转换为从另1 相取电，并将换相区间设为无电区（分相区）以防止发生短路。由于分相区为无电区间，列车在进入分相区前必须断电，且在分相区内采用惰行工况运行。因此，不考虑列车在分相区惰行的操纵方案无法直接应用到实际操纵中。

若要将不考虑分相区惰行模型求解的列车节能操纵方案应用于实际，需对操纵方案进行修改。例如，标准四阶段法[5]未考虑分相区惰行，当修改该方案使其在分相区惰行并在出分相区后重新牵引至原巡航速度，见图2，则巡航转惰行工况点位置较原方案推后（s1＜s2）以满足运行时分要求。这样所得方案虽然可应用于实际，但不一定是最节能的操纵方案，因此有必要直接在建模时考虑列车在分相区惰行的要求。

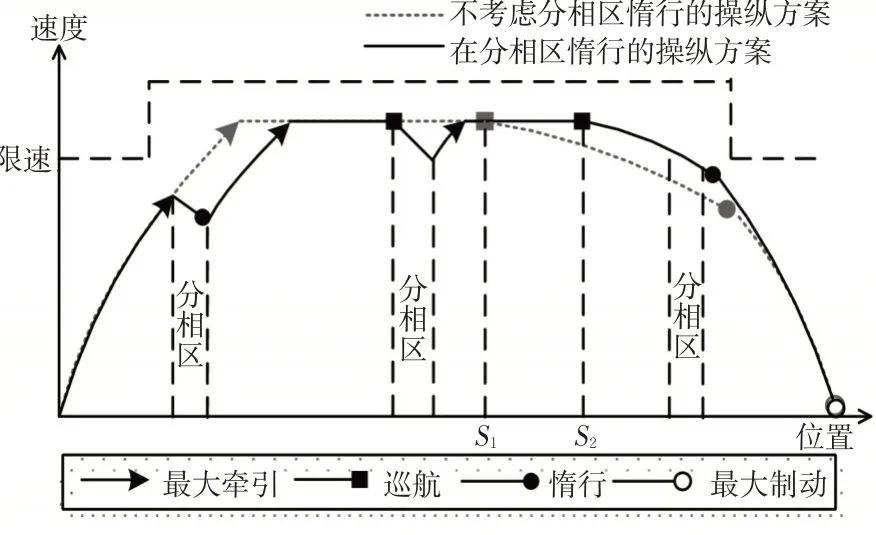
图2 分相区惰行对列车操纵方案的影响示意图Fig. 2 The impact of neutral zones on the train operation

在司机实际驾驶时，为确保列车运行安全，一般在列车车头进入分相区前和列车车尾离开分相区后一段时间（约10 s），列车都处于惰行工况。

2 模型构建

2.1 模型假设

针对考虑过分相区等实际约束的高速列车最优控制问题，本文基于以下假设提出多阶段最优控制模型(multiple-phase optimal control model，MPOC)。

1） 通过对线路坡道进行等效处理[19]，将列车视为一个质点进行计算，不考虑相邻车厢间作用力的影响。

2） 本文研究单列车节能操纵问题，不考虑前、后车对列车运行的影响。

2.2 多阶段最优控制模型

模型的优化目标为最小化列车牵引能耗。

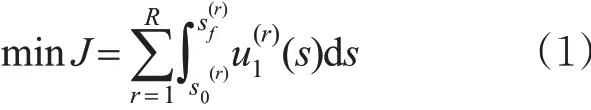
为求解列车运行最优控制问题，首先要对列车运行行为进行描述，建立列车运行模型。根据牛顿第二定律和微分关系，列车在阶段r的运动过程可表示为速度与自变量s有关的导数。

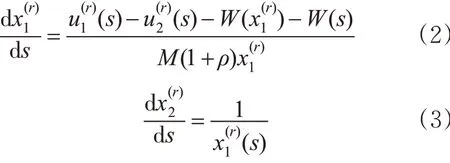
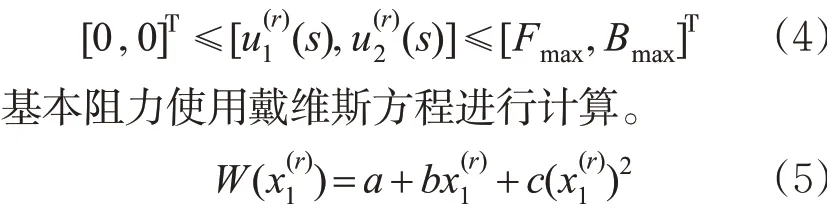
式中:a，b，c为与列车类型有关的常量。

附加阻力通常来源于坡道、曲线，本文将曲线转换为一个固定坡道并加到原坡道上，则附加阻力计算方法为

式中:g 为重力加速度，9.81 m/s2；i(s) 为位置s 处的加算坡度。

按照约束条件是否只要求在某一时间点得到满足，可将其分为点约束和路径约束2种。其中，点约束为只在某一时间点满足的约束[20]，由于运行区间起、终点的状态变量是固定的，因此多阶段最优控制模型的点约束表示为

路径约束是指在某个时间段都必须满足的约束条件[21]，见式（4）。列车从进入分相区前到离开分相区后一段时间内都须断电惰行，属于路径约束。列车惰行时F和B均为0，因此列车过分相区约束可表示为

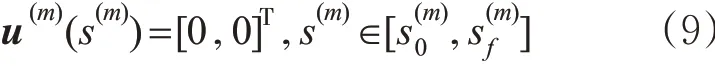
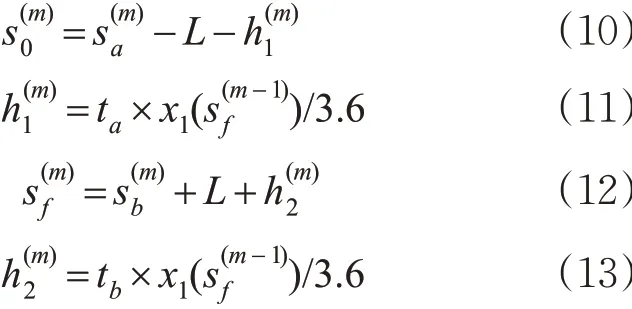
此外，还应始终确保列车运行安全和乘客舒适。为保障安全，列车运行过程中速度不能超过限速

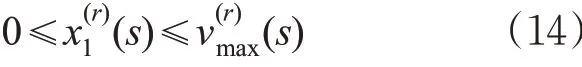
乘客乘车舒适度与列车速度变化有关，速度变化率越大乘客产生不适的可能性越高，因此列车运行加、减速度不能超过给定值

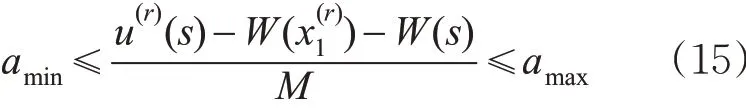
式中:amax和amin分别为最大允许加、减速度，m/s2，通常按照规定取常数。

由于模型将列车运行区间划分为多个阶段，所以还需要通过一些条件对相邻阶段的操纵方案进行连接，才能得到完整的操纵方案。根据线路和时间的连续性，对2个相邻阶段k和k+1，k终点与k+1起点的位置、状态变量是相等的

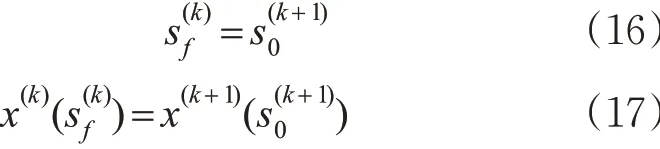
3 算法求解

由于列车运行状况复杂，相邻距离步长的控制变量可能发生突变。相较Gauss 伪谱法，这类解在某些相邻步长内变化较快的最优控制问题能被自适应Radau 伪谱法更高效、精确地求解[21]。因此，针对上述非线性多约束模型，本文选择自适应Radau 伪谱法[18]（以下简称“伪谱法”）进行求解，其基于求解器GPOPS[21]实现。

3.1 MPOC与GPOPS的对应关系

GPOPS是基于伪谱法的Matlab优化工具，其具有固定的结构。GPOPS通常包括主函数、性能指标函数和微分代数方程函数，对多阶段模型，还应指定连接方程函数，本文模型与GPOPS各部分的对应关系见图3。

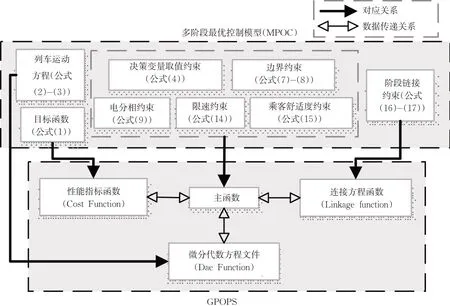
图3 GPOPS结构及与MPOC的对应关系Fig. 3 Structure of GPOPS and the relation between GPOPS and MPOC

由于GPOPS 以列向量方式进行计算以提高运算速度[21]，所以还需将本文模型中的约束转换为列向量形式。其中，式（2），式（3）表示为

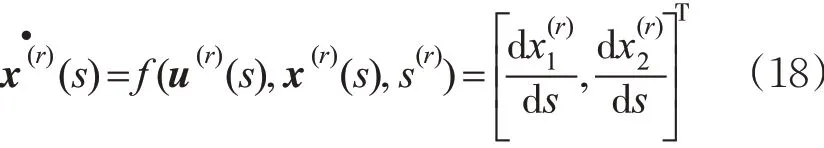
此外，由于决策变量取值约束、限速约束和乘客舒适度约束都为路径约束，这3 类约束可以合并表示为

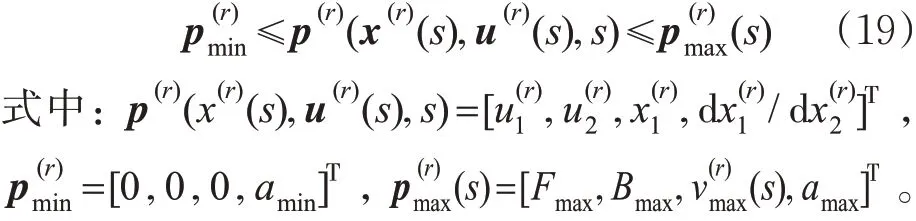
3.2 伪谱法求解列车最优控制问题

伪谱法的基本原理为在[-1,1]上离散控制、状态变量，再借助离散后变量将原问题（连续时间最优控制问题）转换为非线性规划问题（nonlinear programming problem, NLP）进行求解。所以伪谱法的关键步骤为离散变换和非线性规划问题求解。

3.2.1 离散变换

根据利用伪谱法求解的基本原理可知，对多阶段列车最优控制问题进行离散变换并转换为1 个NLP问题可分为4步。

步骤1。将自变量的取值区间映射到[-1,1]上。

步骤2。对控制变量和状态变量进行近似。

步骤3。用新状态变量近似列车运动方程。

步骤4。用新控制变量近似目标函数。

首先对自变量s进行变换将其映射到[-1,1]上。

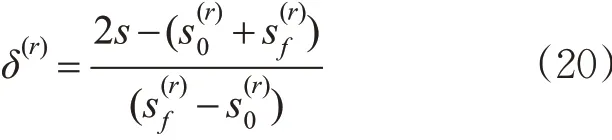
式中:δ(r)为新的自变量且δ(r)∈[-1,1]，其对s 的导数为

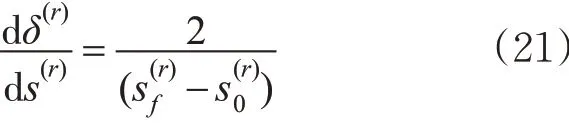
接着近似各阶段r 的控制变量u(r)和状态变量x(r)。伪谱法对变量进行离散变换的基础是插值法，即在某些点（配点）上构造多项式表示连续变量[20]。在此用拉格朗日多项式近似x(δ(r)) 和u(δ(r))。

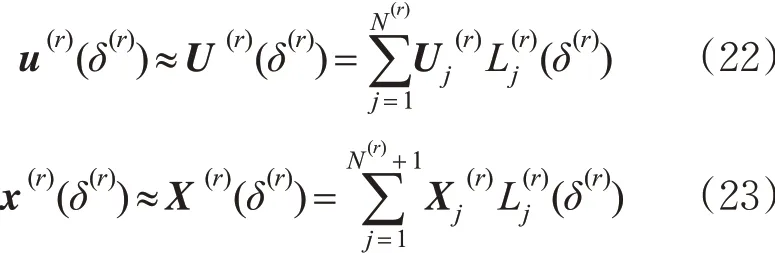
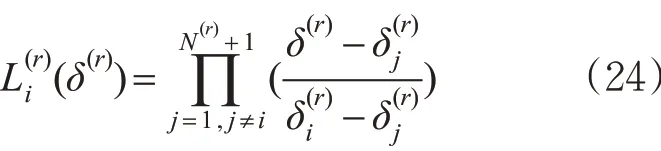
然后利用离散后的状态变量，对列车运动方程进行近似。式（23）对δ(r)求导，得

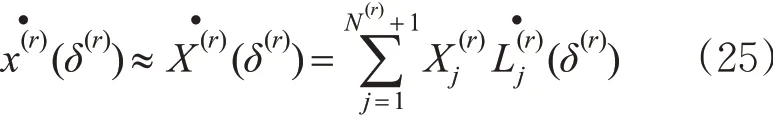
接着结合式（21）和（25），将式（18）在LGR点上离散，即把列车运动方程转换为代数方程。

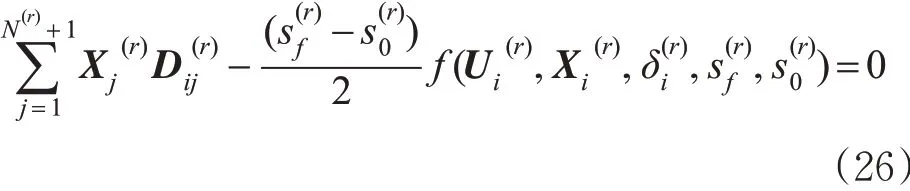
最后，对目标函数进行近似。由于式（1）的右侧为积分项，在此采用高斯积分公式近似目标函数。

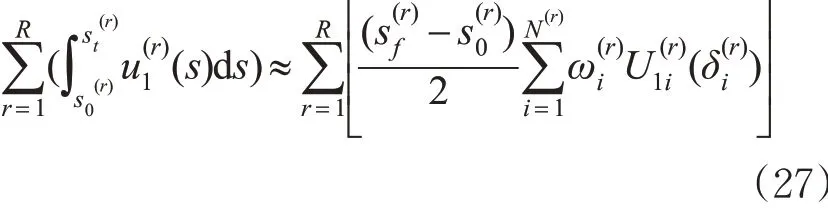
3.2.2 非线性规划问题求解

由于NLP问题规模较大，为快速得到NLP问题的解，需要选择求解能力强的数学规划算法。序列二次规划（sequence quadratic program，SQP）方法被公认为求解复杂NLP 问题的优秀算法之一[21]，在GPOPS 中采用基于SQP 方法的SNOPT 求解器求解离散变换后的NLP问题。

求解NLP问题后，需对各个阶段验算相邻网格点（配点）区间的计算精度是否满足要求（最大误差ε由用户在GPOPS 主函数中输入）。若误差大于ε ，GPOPS将使用hp自适应方法[21]更新网格，并在新的网格上再次进行离散变换和求解NLP问题。

综合以上，GPOPS基于伪谱法求解多阶段最优控制问题的流程图见图4。

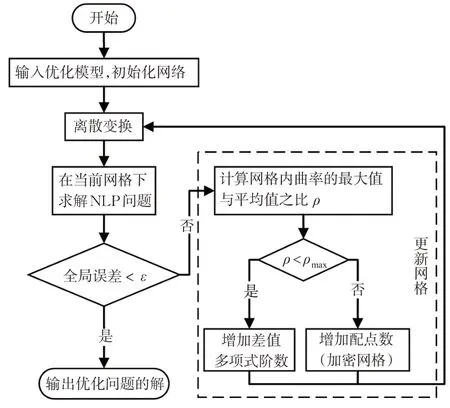
图4 GPOPS求解流程图Fig. 4 Flowchart of GPOPS to solve the proposed model

具体步骤如下。

1） 输入优化模型，自动划分初始网格。

2） 在给定网格下进行离散变换，得到NLP 问题并求解。

3） 检验各阶段相邻网格点形成区间内的点是否满足最大误差ε 。若满足要求，输出解；否则，执行步骤4）。

4） 判断ρ 是否小于曲率阈值ρmax（由用户在GPOPS 的主函数中给定）。若是，说明曲线比较光滑，则增加插值多项式阶数，否则加密网格。更新后返回步骤2）。

4 案例分析

4.1 基础信息

选取武汉—广州高速铁路线路的3个区间进行案例分析，列车采用CRH380A 型动车组。列车和线路参数分别见表1、表2，其中各区间线路高程和分相区位置见图5。按照2.1 中的阶段划分原则，3个站间依次划分为49，23和45个阶段。

表1 列车参数Tab. 1 Train parameters

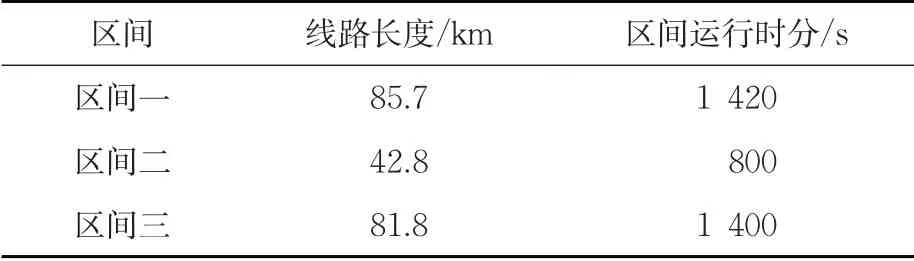
表2 线路参数Tab. 2 Line parameters

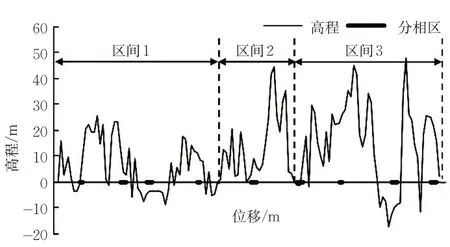
图5 分相区位置及区间高程Fig. 5 Horizontal distances of neutral zones and elevations of sections

案例求解在i5-4200H CPU@2.8GHz 处理器，4GB 内存计算机上的Matlab（R2018b）平台上编程实现，基于GPOPS 求解多阶段最优控制模型。其中，GPOPS中的最大误差ε 取10-6，网格优化的迭代次数为20次，其他参数使用默认值。

4.2 考虑过分相区必要性验证

经理论分析可知，当使用1.2所述方法修改列车节能操纵方案使之满足分相区惰行要求，所得方案（MPOC-C）不一定最利于节能，有必要在模型中考虑分相区约束以最小化牵引能耗。为验证这一必要性，以下将对比MPOC-C和本文模型（MPOC）所求操纵方案及能耗，证明在模型中考虑分相区约束所求操纵方案具有更好的节能效果。

由于MPOC-C 方案由不考虑分相区惰行的列车节能操纵方案（MPOC-N）修改得到，根据阶段划分原则，3个区间依次分为42，21和41个阶段。使用GPOPS 求解得到不同区间上MPOC-N、MPOC-C和MPOC的能耗，结果见表3。

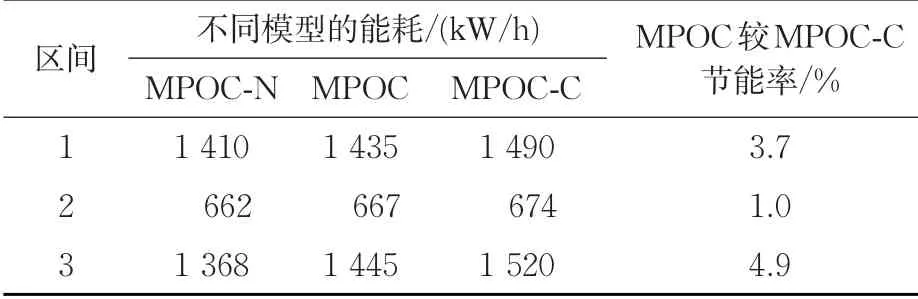
表3 MPOC-N，MPOC-C 和MPOC 能耗对比Tab. 3 Comparison of energy consumption between MPOC-N, MPOC-C and MPOC

由 表3 可 知:相 较MPOC-N，MPOC-C 和MPOC 求解能耗均增加，证明不考虑列车在分相区惰行的模型所求能耗可能偏低；另外，MPOC能耗小于MPOC-C，节能率可达4.9%，表明有必要在模型中考虑列车过分相区约束，更有利于节约列车能耗。

为进一步分析MPOC 的节能原理，MPOC 和MPOC-C 在区间3 上的定时节能操纵方案、能耗变化见图6。

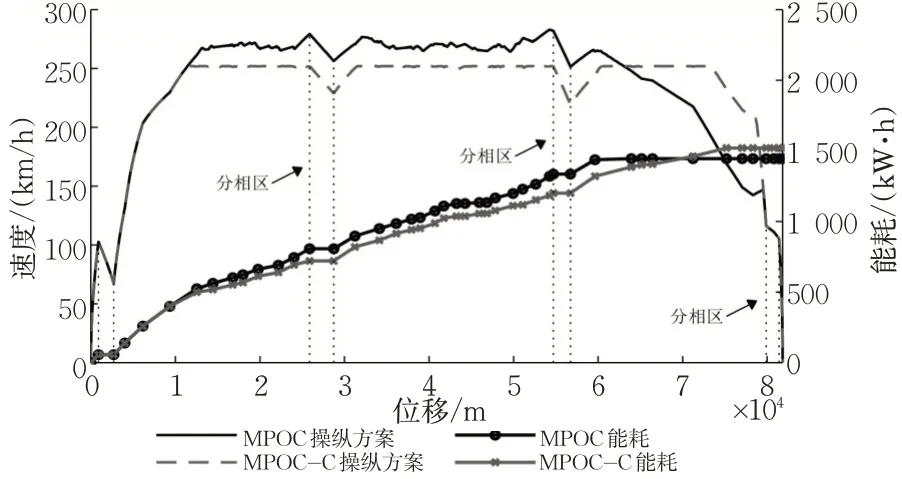
图6 区间3上MPOC-C与MPOC操纵方案与能耗Fig. 6 Train trajectory and energy consumption of MPOC-C and MPOC in section 3

由图6可见:MPOC-C和MPOC的操纵方案在4个分相区均采用了惰行工况，满足实际要求。相较MPOC-C，由于MPOC在模型中直接考虑了列车在分相区惰行约束，所求操纵方案采用更高的巡航速度，从而使得惰行位置提前，减小了列车为保持巡航工况而使用牵引力的时间，最终实现牵引能耗的节约。

4.3 模型节能效果验证

本节将MPOC方法与司机人工操纵（采集自现场，EHD）、考虑分相区惰行的标准四阶段方法[15]（SFS）进行对比，说明本文方法的优化效果。SFS的操纵策略为采用最大牵引力牵引至允许速度（案例中为290 km/h）并保持该速度运行，再根据富余时分采用二分法搜索巡航转惰行点以满足定时约束，具体见文献[16]。由于文献[16]采用遗传算法求解SFS模型，所得解不一定为最优解，所以引入暴力搜索算法（步长为1 m）求SFS 模型的精确解，以保证比较的公平性。

司机操纵能耗和SFS、MPOC 的能耗结果见表4。可知相较司机人工驾驶，SFS 和MPOC 的操纵方案更加节能，且MPOC 在不同坡道（3 个区间）上都具有最好的节能效果。为说明MPOC 方法的节能原因，以区间1 为例，司机操纵方案和SFS，MPOC求解的节能操纵方案见图7。

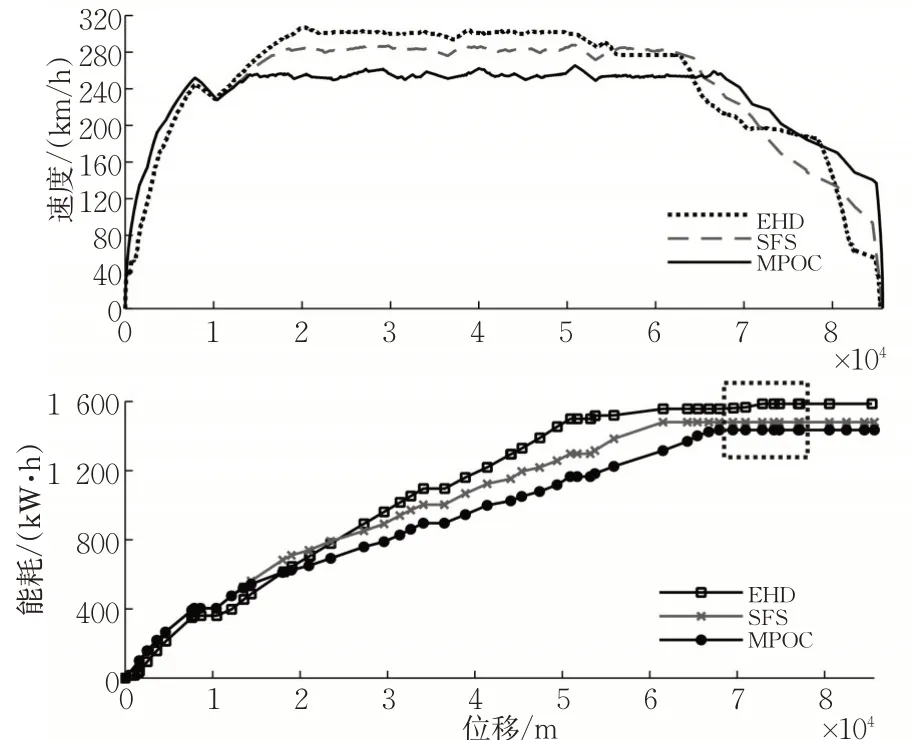
图7 区间1上司机操纵方案和SFS、MPOC求解操纵方案（上图）及能耗（下图）对比Fig. 7 Train trajectory (upper plot) and energy consumption（lower plot）of EHD，SFS and MPOC in section 1

由图7 可见:EHD 和SFS方案的巡航速度比较接近，但由于司机根据经验选择的工况转换点难以保证最优，EHD由巡航工况转为惰行工况一段距离后，又进行2次牵引导致能耗进一步增加（见图7中虚线矩形框）。相较SFS方案，MPOC方案采用更低的巡航速度，在列车出站牵引阶段使用更少的能耗，且在巡航过程中列车所受基本阻力更小，降低了用于克服阻力做功所用牵引能耗。虽然为满足运行时分要求，MPOC 方案的巡航转惰行工况点较SFS 推后，但最终仍比SFS方案更加节能。结果表明MPOC考虑分相区、运行时分等采用最优的巡航速度，所求操纵方案较EHD和SFS具有更好的节能效果。

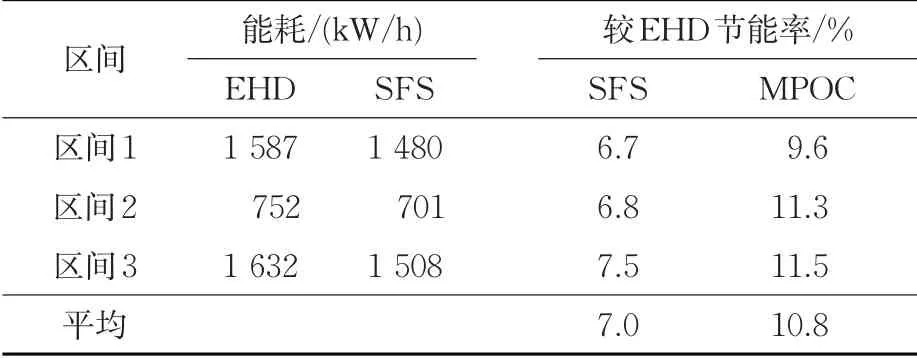
表4 EHD，SFS 和MPOC 能耗对比Tab. 4 Comparison of energy consumption between EHD,SFS and MPOC

由于列车节能操纵方案受区间运行时分影响，为进一步说明MPOC方法的通用性，对不同运行时分下MPOC 和SFS 的节能效果进行研究。不同富余运行时分下MPOC较SFS的节能率见图8。由图可知，在不同线路条件、区间运行时分下，MPOC 能耗都不高于SFS，且富余时分较大时，MPOC的节能效果更好。这是因为当富余时分较小时，为满足运行时分要求，MPOC方案需采用较高的巡航速度，与SFS所求优化方案类似。

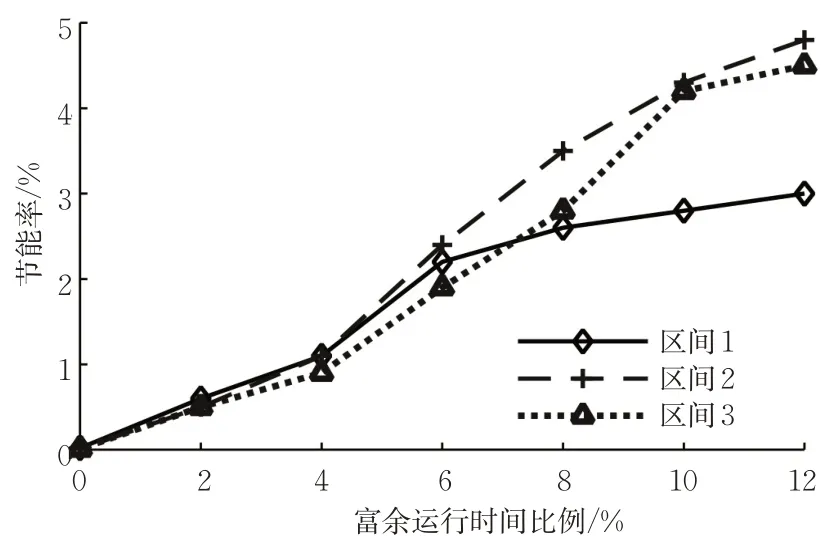
图8 MPOC较SFS节能率随富余时分变化图Fig. 8 Energy-saving effect of MPOC at different runtimes

此外，由于高速铁路站间距大，精确求解高速列车定时节能操纵方案所需时间较长，为验证MPOC方法求解的高效性，不同区间采用MPOC和SFS方法的求解时间见表5。结果表明MPOC方法的求解效率更高，尤其在区间长度较大时（区间1和区间3）节约的求解时间较多，宜用于求解区间长的高速铁路列车节能操纵方案。

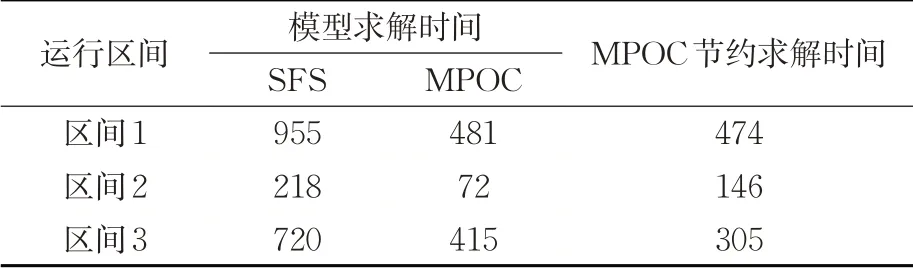
表5 MPOC 与SFS 求解时间对比Tab. 5 Computing time of MPOC and SFS s

5 结束语

1） 有必要在列车节能操纵模型中考虑列车过分相区约束，不仅符合现实操纵要求，而且直接在模型中考虑过分相区约束所得方案在节能方面的表现优于“修改不考虑过分相区约束模型所得解”使其符合实际约束的方案。

2） 本文模型得到的操纵方案相较司机人工驾驶方案的区间平均节能率为10.8%，相较考虑过分相区的标准四阶段模型所得操纵方案的区间平均节能率为4%且求解时间减少。

3） 由于列车实际运行还受到前、后车的影响，而本文研究问题为单列车节能操纵优化，因此下一步将研究考虑过分相区约束的多列车操纵优化。