基于模型预测控制的车道保持策略研究与应用

蒋立伟 檀生辉 吴 勇

（西安电子科技大学芜湖研究院，安徽芜湖241000）

1 车辆动力学模型的建立

首先，在如下假设的前提下，建立车辆的二自由度动力学坐标系和模型，如图1所示：（1）不考虑车辆在Z轴方向的运动，只考虑在X、Y水平面的运动；（2）左、右侧车轮转角一致；（3）车辆行驶速度变化缓慢，忽略前后轴载荷的转移；（4）车身及悬架系统是刚性的；（5）转向时转角直接输入给转向轮。

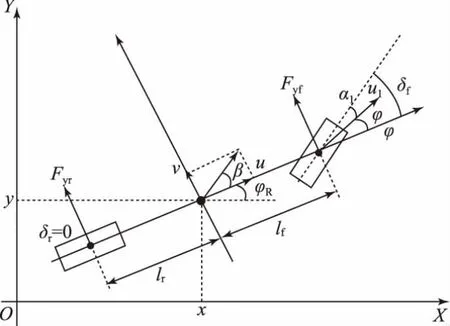
图1 车辆的二自由度动力学坐标系和模型

然后，按如下3个步骤建立车辆动力学模型：

（1）确定汽车质心绝对加速度在车辆坐标系上的分量ay：

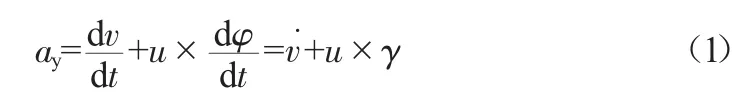
式中：v为车辆沿y轴的速度；u为车辆沿x轴的速度；φ为车辆横摆角（偏航角）；γ为横摆角速度。

（2）确定车辆受到的侧向力∑Fy和横摆力矩∑Mz，前角转向δf很小，后角转向δr=0。

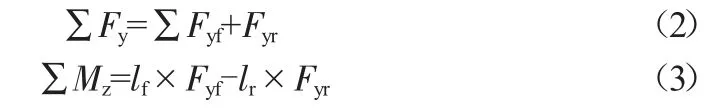
式中：lf、lr分别为前后轴到质心的距离。

前、后轮侧偏力为：

式中：k1、k2分别为前后轮侧偏刚度；αf、αr为侧偏角。

由上述公式得到前后轮侧偏角：

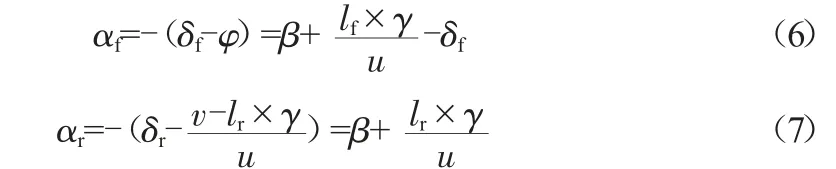
式中：β为质心侧偏角；φ为车辆横摆角（偏航角）；δf为前角转向；δr为后角转向；γ为横摆角速度。

（3）建立外力、外力矩与汽车运动参数的关系及运动微分方程：

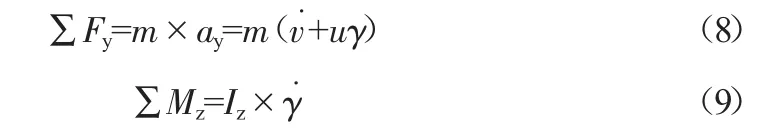
式中：m为整车质量；Iz为车辆绕过质心垂直轴线的转动惯量。

将式（6）～式（9）整理后得到车辆动力学模型如下：

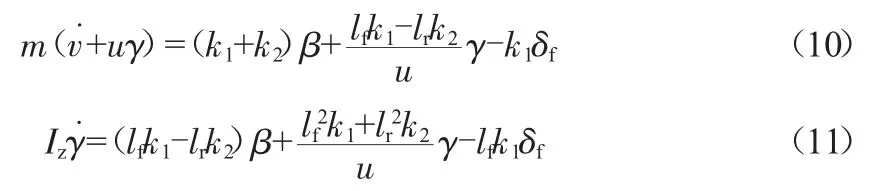
在车辆动力学的基础上，还需建立侧向偏差y、航向角偏差φ和动力学方程之间的关系，车辆运动与道路关系模型如图2所示。

图2 车辆运动与道路关系模型

其中，φR为道路航向角；φV为车辆航向角，联合式（10）、（11）建立系统的状态方程如下：

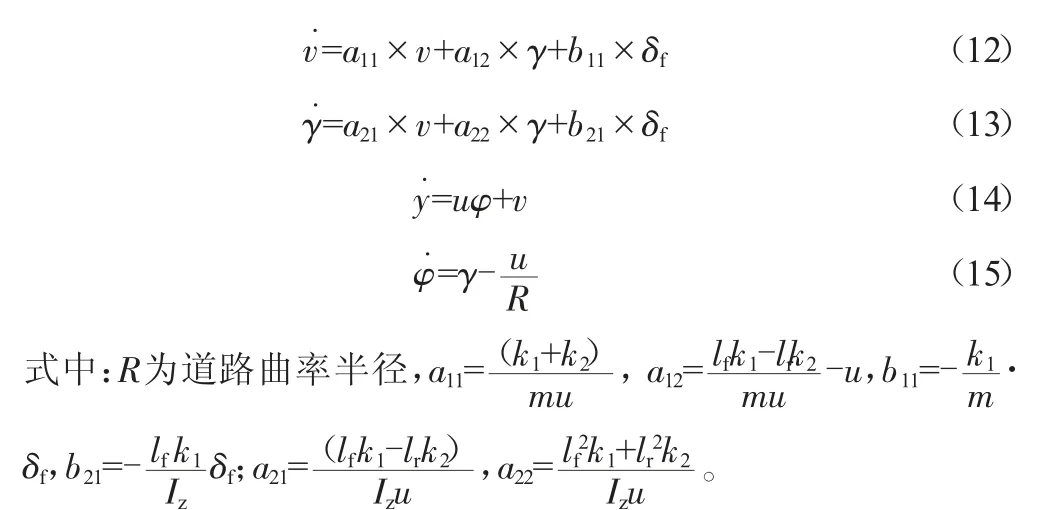
进一步整理得：

其中：

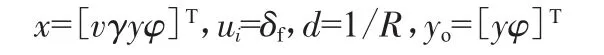
定义：状态变量为侧向速度v、横摆角速度γ、侧向偏差y、航向角偏差φ。控制输入为前轮转角δf，已知输入为道路半径R。

2 基于模型预测控制的车道保持策略建模

基于模型预测控制车道保持策略主要包含：模型预测、滚动优化和反馈矫正、目标横向偏差、横摆角偏差控制模块和纵向控制模块。

车道保持是通过检测车辆与道路中心线的横向偏差和横摆角偏差来控制车辆的方向盘的转角，最终使车辆行驶在道路中心线上，其中所用的车辆参数整车质量m=1 270 kg，绕Z轴转动惯量Iz=1 536.7 kg·m2，前后轴距lf、lr分别为1.015 m、1.895 m，前后轮侧偏刚度k1、k2都为180 000 N/rad。

2.1 模型预测

模型所需相关的参数如下所示：

将上一章节中的状态方程模型式（16）（17）进行离散化，得到：

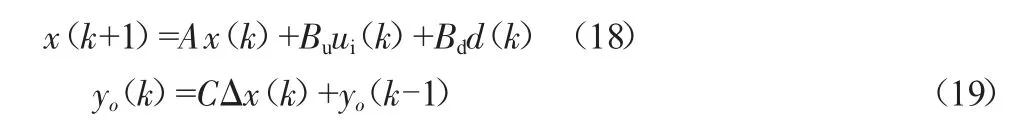
以最新测量值为初始条件，预测时域为p，控制时域为m，得到：Δx（k+1/k）=AΔx（k）+BΔui（k）+BdΔd（k），表示第k个时刻对第k+1个时刻的状态预测，进一步输出方程为：

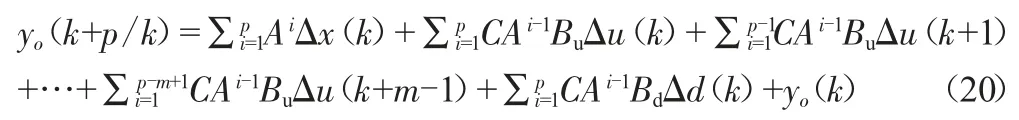
那么，对系统未来p步预测的输出为：

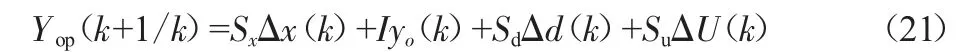
2.2 滚动优化模型

得到车辆模型在预测时域内的预测输出后，建立模型预测输出与期望输出之间的偏差和控制量及其变化率的二次型目标函数，具体如下所示：

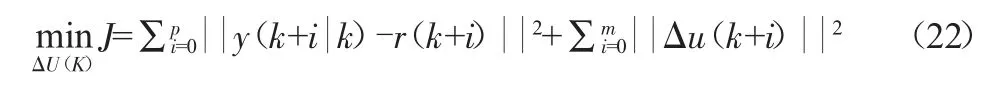
其约束条件为：

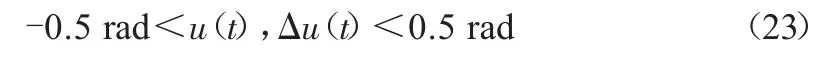
其中，y（k+1）为目标参考序列，即期望的目标横向偏差和横摆角偏差序列，可通过对状态方程（14）（15）积分得到，作为控制模型的输入，如图2所示。通过二次规划的方法可以求解出最优的控制量即前轮偏角。最后通过在每个控制周期不断地求解最优的控制量，形成滚动优化过程。

2.3 反馈矫正

反馈矫正是通过比较模型输出与实际对象输出之间的偏差来修正模型的预测输出。

2.4 目标横向偏差和横摆角偏差模块

作为目标参考序列的期望的目标横向偏差和横摆角偏差序列，可通过对状态方程积分得到作为控制模型的输入，如图2所示。

2.5 纵向控制模块

纵向控制是对设定的目标车速进行PID闭环控制，使车辆保持稳定车速行驶。

3 整车Carsim模型搭建

首先，根据整车参数搭建整车模型，如图3所示，然后根据控制需求添加接口，整车的输入接口包括方向盘转角、节气门开度和制动压力，输出接口包括纵向速度、横向速度、横摆角速度、道路曲率。设计道路模型，包括直道、半圆道、正弦道，总计3.9 km。

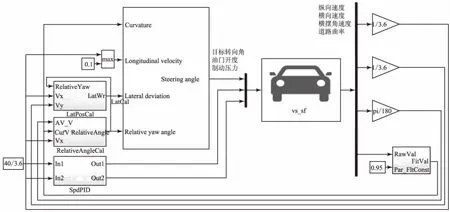
图3 车道保持模型在环仿真系统

4 控制模型与整车模型集成测试

4.1 模型在环仿真测试

将第2节开发的基于MPC的车道保持控制模型与第3节搭建的整车模型在Matlab/Simulink环境中进行集成和联合仿真测试。

模型开始运行后，车辆以40 km/h的车速在道路上匀速行驶，仿真结果如图4所示。

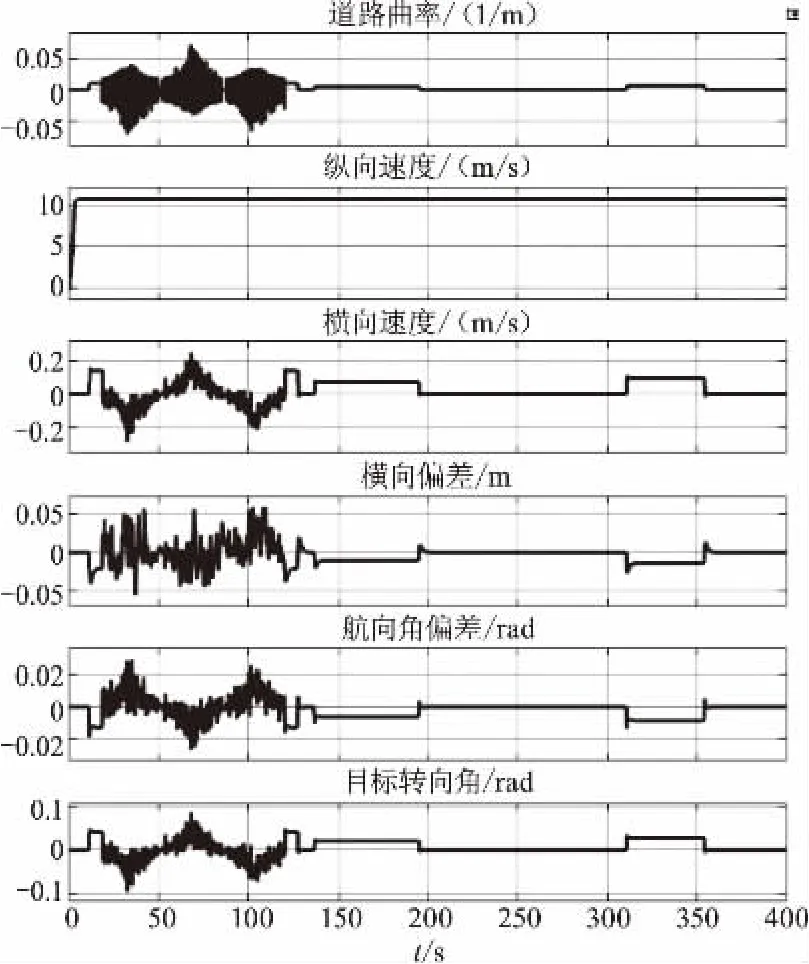
图4 车道保持控制系统过程数据

从图4过程数据可以看到，车辆开始从直道上行驶至10.5 s变为弯道，到18.2 s后变为正弦道路，由于车辆检测到道路曲率的变化，目标转向角根据道路曲率开始调节，使车辆保持在道路中心位置，在此过程中，道路曲率、横向速度、侧向偏差、航向角偏差也随之平稳变化，直到120 s后又进入弯道，如此按照预定的道路行驶，直到行程结束。

在整个行驶过程中，最大侧向偏差不超过6 cm，目标方向盘转角在-0.1～0.1 rad内平稳变化，满足约束条件。基于MPC的车道保持控制效果如图5所示。

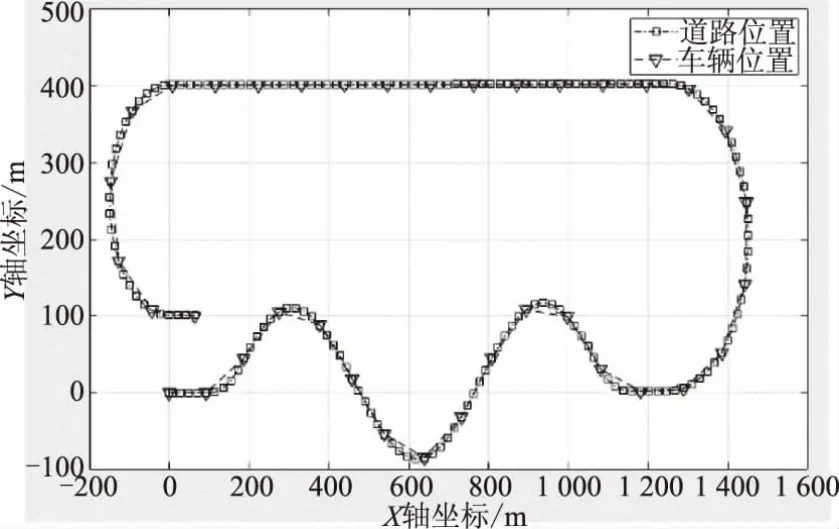
图5 基于MPC的车道保持控制效果

从图5的控制效果可以看到，通过基于MPC的车道保持控制，车辆的位置曲线和道路的位置曲线能高度重合，即较好地实现了车道保持控制。

4.2 实车道路测试

将图3中浮点的控制模型通过定点化和接口配置之后，生成C代码与嵌入式处理器的基础软件集成、编译，并将可执行文件刷写到ADAS ECU中运行，车道保持实车测试结果如图6所示。

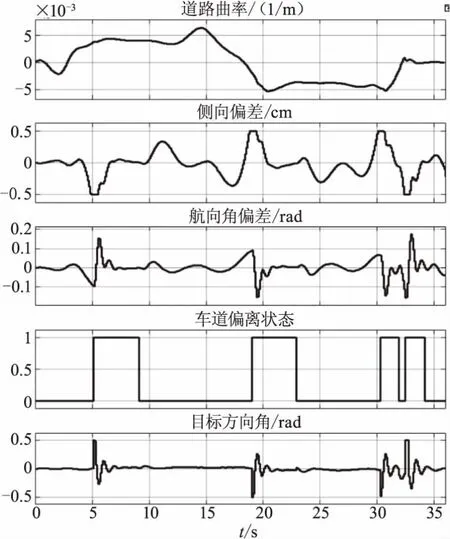
图6 车道保持实车测试结果

控制模型输入所需的道路曲率、车辆航向角等信号，通过CAN总线从感知信号处理的域控制器获取，同时将目标转角控制指令发送给电动助力转向控制器执行，实现车道保持。如图6所示，车辆在行驶过程中，运行基于模型预测控制的车道保持策略的ADAS ECU综合道路曲率、航向角偏差和侧向偏差，给出车道偏离状态，并根据车道偏离状态对转向系统进行快速控制。在整个试验过程中，最大侧向偏差不超过5 cm，转向角控制量超调较小且快速达平稳状态，使车辆始终保持在道路中间位置行驶。

5 结语

本文针对辅助/自动驾驶车道保持系统，提出了一种基于模型预测控制（MPC）的车道保持控制策略。在车辆动力学和状态方程的基础上，开发了基于模型预测控制的车道保持控制策略，并与整车模型进行集成以及模型在环仿真测试，之后通过代码生成和集成，将控制策略刷写到实际ADAS ECU中进行实车道路测试、验证和应用，试验结果表明，在各种道路环境中，该控制策略始终能使车辆保持在道路中间行驶，具有良好的控制效果，提高了车辆的操纵稳定性，保证车辆行驶的安全性和舒适性。