基于贝叶斯网络的发动机推力振荡故障诊断研究

胡 建，蔡 景，胡 维

(南京航空航天大学民航学院， 江苏 南京 211106)

航空发动机控制系统是航空发动机的重要组成部分，为了保证飞机安全飞行，对发动机动力控制提出了更高的控制和精度要求。随着电子技术的快速发展和日趋完善，全权限数字电子式控制(full authority digital electronic control， FADEC)已发展成为航空发动机首选。FADEC由大量的电子元件、传感器和执行机构组成，由于传感器工作于高温、高压、强振动的恶劣环境中，因此故障率较高。发动机推力振荡是一种比较常见的故障类型，由于故障原因非常复杂，并且故障检查比较困难，因此在发动机故障诊断中备受关注[1-3]。为了尽快排除故障，实际应用中，维修人员的排除故障的工作大多是基于FADCE的运行状态或维修手册上列出的步骤进行检查。由于状态监测无法具体到每个部件[4-5]，因此维修人员只能根据经验和手册进行逐一排查，导致效率较低，工作量大，时间成本高[6]。如果能建立故障诊断模型，依据故障表征快速排查故障源，将会节省大量时间，同时可以减少故障保留率和航班延误率。

贝叶斯网络在解决不确定性和关联性的问题方面有着自己特有的优势，并且能够很好地应对故障信息不完备、数据容错能力不足的问题。程雨[7]利用贝叶斯网络实现列控系统故障诊断和维护，提高了故障数据不完整和非确定决策情况下故障诊断精度，优化了维护策略，提高了系统的安全性、可靠性、可用性和可维护性。王丹[8]在故障树分析方法的基础上引入贝叶斯网络分析方法，以转向架系统中的基础制动装置系统为对象，对故障贝叶斯网络进行精确推理。冯锋[9]将贝叶斯网络引入电网故障诊断中，大大提高了诊断效率，弥补了传统诊断方法仅依靠开关量造成诊断精度不高的问题。因此贝叶斯网络在故障诊断中已经得到了大量的应用，但在航空发动机关注的推力振荡故障方面的研究还没有开展过。

为此，本文基于贝叶斯网络原理，针对发动机推力振荡故障问题，以燃油计量振荡为顶事件建立故障树，在此基础上通过研究故障树与贝叶斯网络的转换方法，建立基于贝叶斯网络的故障诊断模型，开展故障诊断研究。

1 贝叶斯网络建模

1.1 建立故障树

故障树分析法(fault tree analysis，FTA)是安全系统工程中比较重要的分析手段，多应用于可靠性、安全性分析和故障诊断中。故障树是根据研究对象和系统中事件之间逻辑关系来建造树状的逻辑图，通过树状的逻辑图可以判断每一个事件发生的概率和原因。

发动机推力振荡的原因非常复杂，但主要原因是燃油计量振荡引起的，因此本文将燃油计量振荡作为顶事件建立故障树，根据燃油计量的部件组成和设计、工作原理，建立了如图1和图2所示的故障树。

图1 燃油计量振荡故障树图

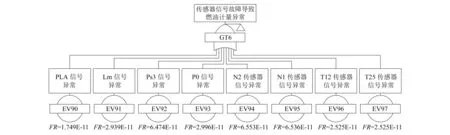
图2 传感器信号故障树

1.2 故障树与贝叶斯网络的转换

贝叶斯网络可以用概率图进行表达，概率图在人工智能、统计学、机器学习等方面广泛使用，它可以清晰地展现出每个变量与其他变量之间的关系，快速处理问题的不确定性。图3是一个简单的贝叶斯网络模型图，其是由5个节点组成的有向无环图，每个变量都转换成了概率图中的节点，因果关系则由有向线段表示出来。

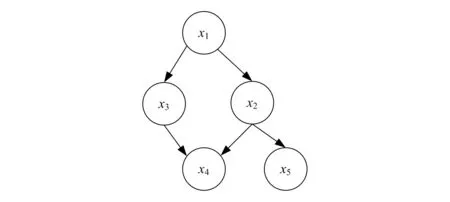
图3 简单贝叶斯网络模型图

该贝叶斯网络中两个相关联的节点的概率关系可以条件概率表进行表示，基本节点可以用先验概率进行表示。

因此该贝叶斯网络的联合概率为：

P(x1,x2,x3,x4,x5)=P(x1)P(x2|x1)·

P(x3|x1)P(x4|x2,x3)P(x5|x3)

(1)

式中：x1,x2,x3,x4,x5分别为5个基本节点，对应的P(·)为节点的概率。

由公式(1)可知，根据贝叶斯网络可以算出每个节点的联合概率。

根据故障树与贝叶斯网络的转换方法，可以将燃油计量振荡故障树中的逻辑门转换为贝叶斯网络对应的关系式，图4和图5分别将逻辑门GT5(燃油作动部件故障导致计量活门位置异常)和 GT34(燃油计量振荡)中对应子节点转化为条件概率。

图4 逻辑门GT5对应的条件概率

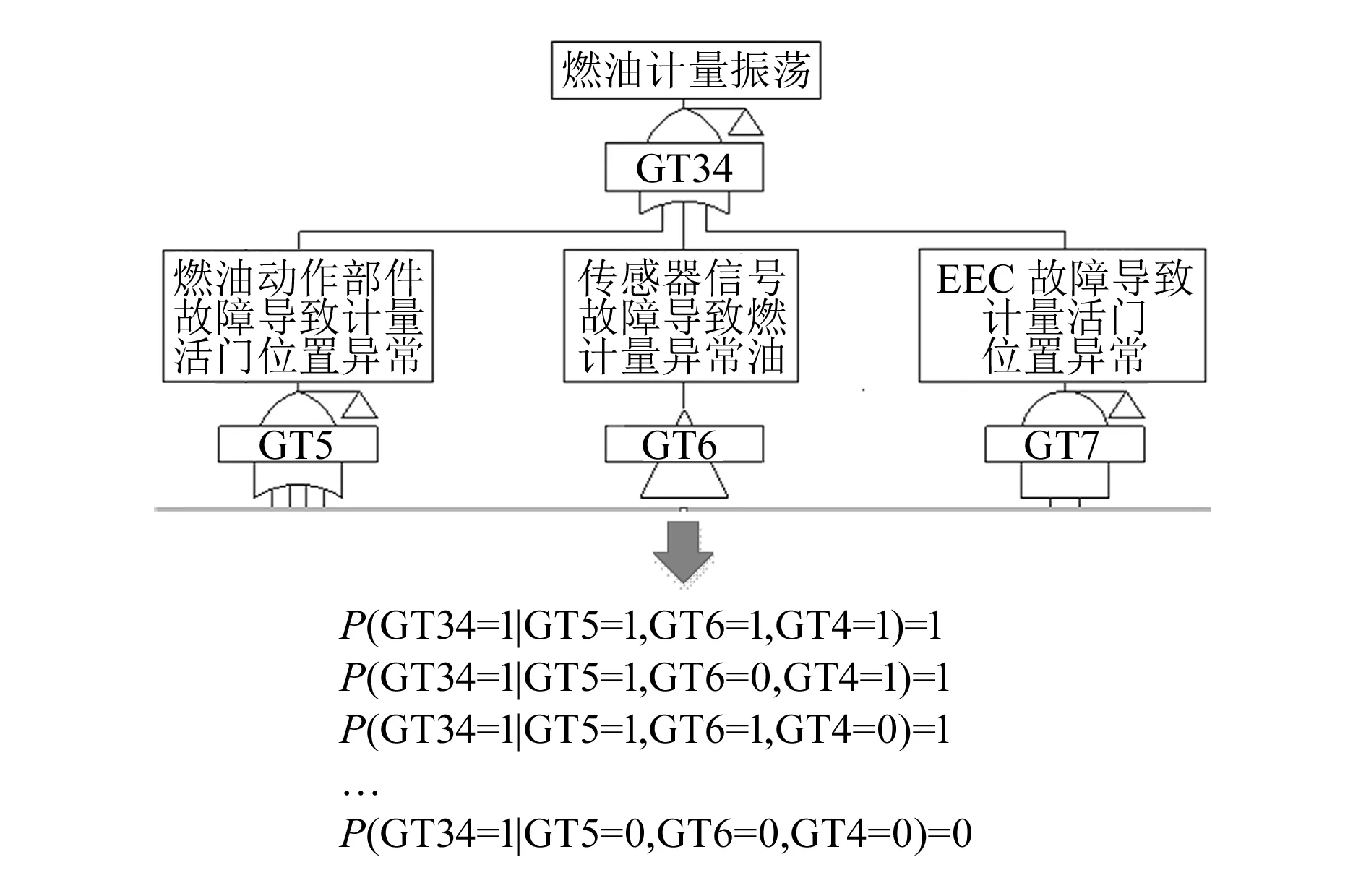
图5 逻辑门GT34对应的条件概率

按照故障树中的逻辑门，用有向线段连接贝叶斯网络中的节点，输出事件作为下一节点的父节点，以此类推，最后得到燃油计量振荡的贝叶斯网络图，如图6所示。

1.3 贝叶斯网络模型

根据图6，在软件Netica中可以构建如图7所示的贝叶斯网络模型。

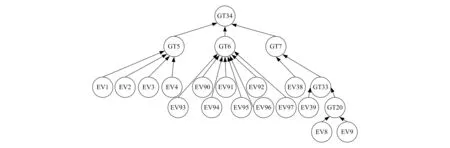
图6 燃油计量振荡的贝叶斯网络图

由图7可以看出，每个节点都有两个模式，即故障和正常。由于Netica显示有效数位过短，所以在界面中显示燃油计量振荡的故障概率为0+。

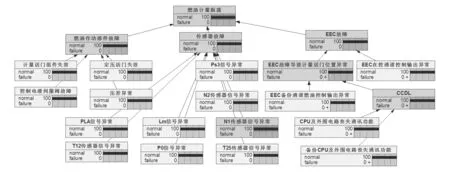
图7 燃油计量振荡贝叶斯网络模型

2 基于贝叶斯网络的故障分析

Netica中建立的贝叶斯网络模型是以贝叶斯概率理论为基础的，用于对节点的后验条件概率分布进行计算[10]。因此，建立的燃油计量振荡贝叶斯网络模型，可以根据基础事件的先验概率和中间节点条件概率求出引起燃油计量振荡故障的各个故障原因的后验概率，诊断分析出造成该故障的根本原因，从而对故障案例进行分析验证，计算出当燃油计量振荡出现故障之后引发该故障的部件故障的后验概率，进而根据引起该故障的后验概率大小，判断得出各个部件故障的可能性[11]。

结合燃油计量振荡的故障案例，对贝叶斯网络模型的诊断验证过程如下：

1)当燃油计量振荡发生故障时，将逻辑门GT34的状态改为故障状态，即“failure”=100%，此时模型中各个节点的参数会根据该参数的变化沿着连接线段自动进行调整。图8为逻辑门 GT34状态更新后的贝叶斯网络模型。

2)由图8可以看出，节点GT34状态改变之后，该模型中各个节点的参数都发生了改变。此时GT5的故障概率已经增长为接近100%。由于燃油作动部件故障又包含了多个部件，从图8可以看出，定压活门失效的概率最大，达到了65.5%，因此对定压活门进行检查。检查结果发现定压活门工作正常。因此，将模型节点EV41(定压活门失效)的参数改为正常，即“normal”=100%，状态更新后的贝叶斯网络模型如图9所示。

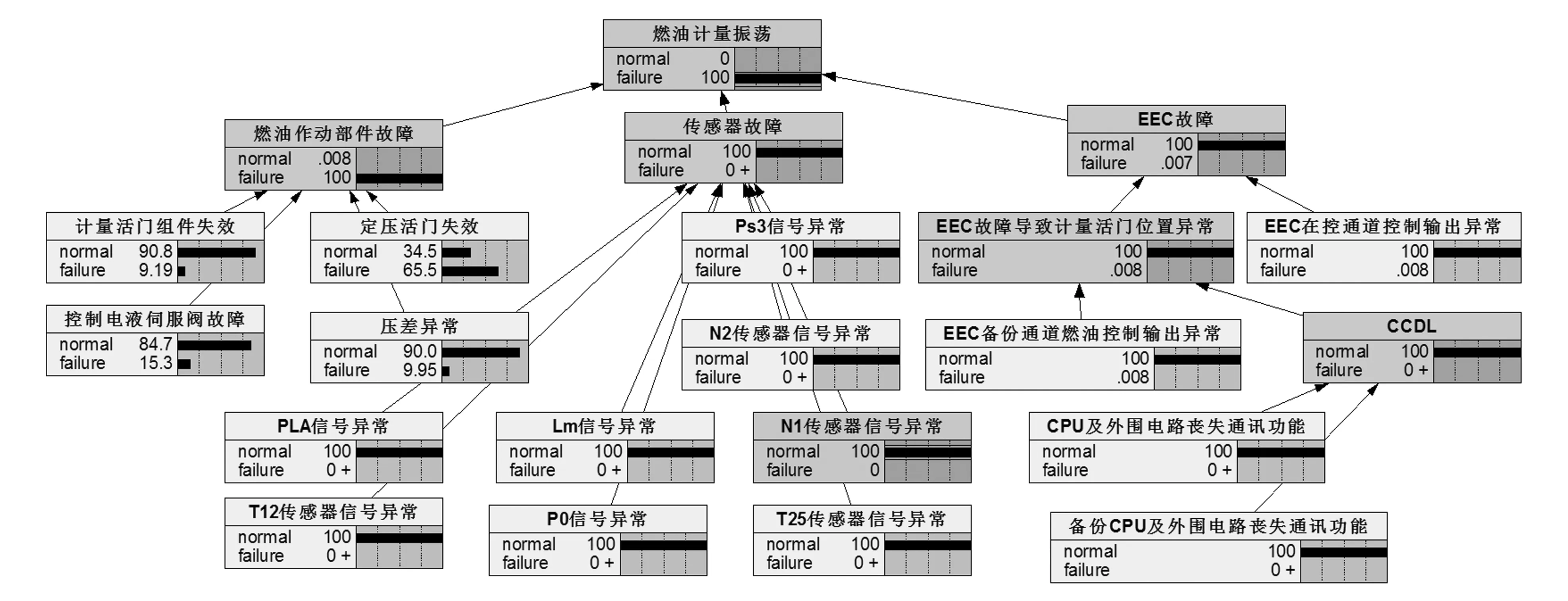
图8 GT34状态更新后的贝叶斯网络模型

3)由图9可以看出，事件节点EV41状态改变之后，该模型中各个节点的参数都发生了改变。此时EV2(控制电液伺服阀故障)的故障概率增长为44.4%，EV3(计量活门组件失效)的故障概率增长为26.7%。因此，对控制电液伺服阀EV2进行检查，检查结果显示工作异常。

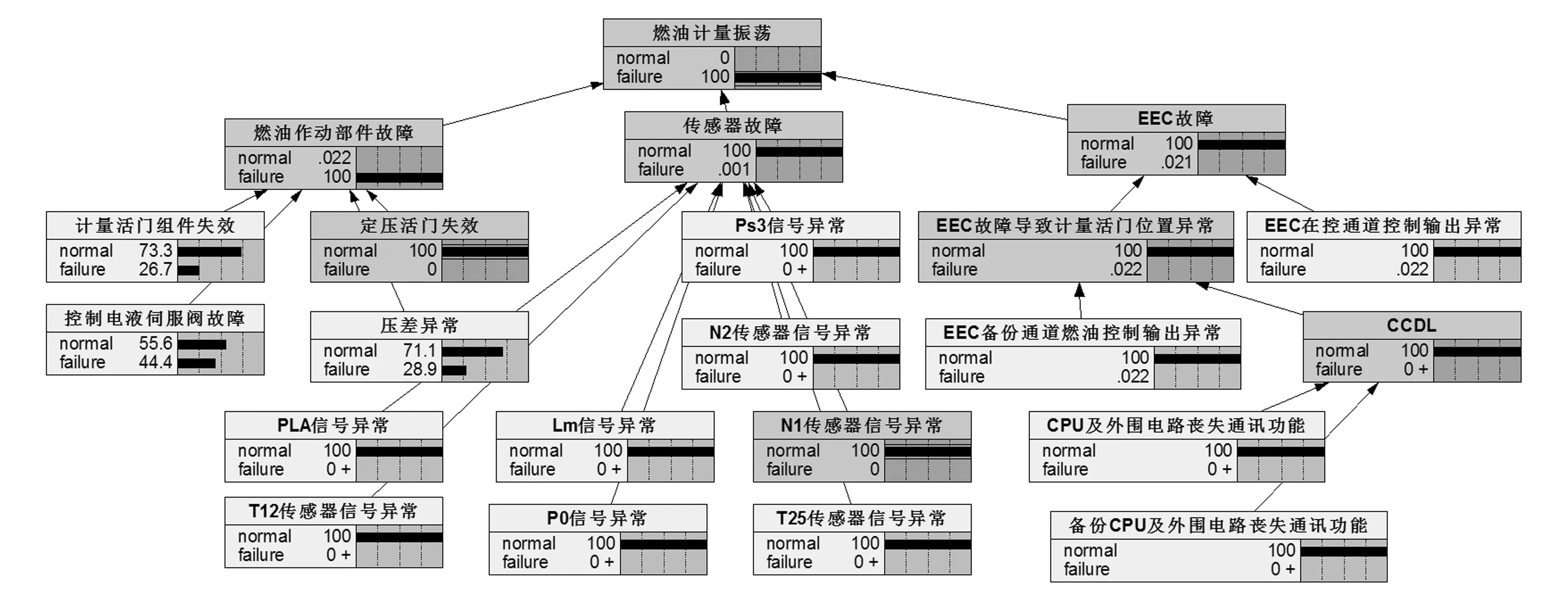
图9 EV41状态更新后的贝叶斯网络模型

经过两次状态更新之后，就可以检查到故障部件。相比于实际中按照经验和手册的方法平均减少了1～2个步骤，有效减少了不必要的检查步骤，节省了时间和人工，提高了故障诊断的效率。

3 结束语

由于发动机的复杂性，当出现一些不常见的故障时，排除故障的过程过于繁琐，往往造成不必要的时间浪费。本文将故障树与贝叶斯网络相结合开展了故障诊断技术研究。研究结果表明，基于贝叶斯网络模型的故障诊断方法，通过少量有针对性的检查就能够对故障做出较准确的诊断，提高了故障诊断效率，同时为编写或改善新发动机维修手册提供一定的参考。