基于非平稳振动信号识别的船舶推进轴系故障诊断方法

金兰

摘要：针对船舶推进轴系维修保障的需要，提出一种船舶推进轴系非平稳振动信号识别的方法，通过求解瞬时频率的改进LMD时频分析，结合参数化时频熵算法提取多分量复合非平稳振动信号的特征，采用仿真信号进行验证分析，并搭建轴系实验台架进行实验验证，实现船舶推进轴系故障诊断。

关键词：船舶推进轴系;非平稳振动信号，LMD时频分析;参数化时频熵;故障诊断

Research on fault diagnosis of propulsion shafting based on identifying the non-stationary vibration signal

Abstract：According to the need of ship propulsion shafting maintenance support， an innovative method of identifying ship propulsion shafting non-stationary vibration signal is proposed. The improved LMD time-frequency analysis is used to solve the instantaneous frequency. The characteristics of the multi-component composite non-stationary vibration signal are extracted by using the parameterized time-frequency entropy algorithm. The simulation signal is used for verification and analysis， and the rotor experimental platform is built and the fault diagnosis of propulsion shafting is realized by experimental verification.

Key words： propulsion shafting; non-stationary vibration signal;LMD time-frequency analysis; parameterized time-frequency entropy; fault diagnosis

0前言

推進轴系作为船舶的主要动力设备，以稳定的输出和高效的效率在海上运输业中占据着不可忽视的作用[1]。但工程实际中经常会出现非平稳振动信号，例如加减速过程、变功率输出等。同时大部分轴系故障的振动信号呈现多分量复合特征，导致传统的故障诊断方法难以进行特征识别和提取[2]。针对该问题，提出一种可靠的、能够对多分量复合非平稳振动信号进行识别和特征提取的方法，以保障旋转机械设备运行的安全性和稳定性。

1非平稳振动信号识别方法

1.1 改进的非平稳振动信号分析

对非平稳振动信号的识别和分析通常采用局域均值分解（Local Mean Decomposition，LMD），对局部时间特征尺度进行划分，得到由包络信号和调频信号相乘的PF分量，LMD是一种自适应时频分析方法[3]，其具体流程如下：

Step 1：求解局部均值函数 ;

Step 2：求解包络估计函数 ;

Step 3：求解纯调频信号 ;

Step 4：求解包络信号 ;

Step 5：求解PF分量。

通过LMD分解对复杂非平稳振动信号进行分解，然后求解单一PF分量的瞬时频率并绘制成时频谱图。

利用LMD得到的时频曲线上存在毛刺、失真等缺陷，提升PF分量瞬时频率的求解效果可改善该问题，对于提高LMD时频分析对多分量复合非平稳振动信号的识别能力尤为重要[4]。改进方法如下：

Step 1：对信号中的极值点进行调整，将其幅值调整为最接近的1或-1;

Step 2：为避免奇异点与毛刺的出现，求出幅值跳跃的差值 ，其中 为信号中的极值点;

Step 3：采用非均匀缩放使曲线更平滑;

（1）

其中 为邻域内点到 的距离，最后将邻域内的所有点都加上经过缩放的差值 。

（2）

Step 4：进行重组得到重构后的纯调频信号 ，对其进行相位求解、展开和求导，最终得到经过修正后的瞬时频率。

1.2非平稳振动信号识别方法

使用参数化的时频熵方法计算不平衡振动信号时频熵，令时频平面有n个面积相等的时频块，其中含有频率成分的时频块有 个，单个时频块内的能量为：

（3）

其中 为瞬时能量，T1、T2为该时频块的起始和结束时间。然后对每一个时频块进行能量归一化，得到 ，其中 为整个时频面的总能量且 。不同的信号在时频平面上具有不同的能量分布状态，可以得到不同的时频熵 。

（4）

基准状态可定义为平稳状态下的单分量信号，此时信号中的能量均集中于基频，每一个含有频率成分的时频块内的能量均为 ， 与 的计算公式如下：

其中 为含有频率成分的时频块数量， 与 为第i个时频块的起始与结束时间， 为标准的时频块基准能量值。利用检测信号每一个含有频率成分的时频块的能量减去基准值 ：

其中 为检测信号时频平面上含有频率成分的时频块个数，将差值累加并平均到每个时频块中求得时频熵。

2 实验设计与故障诊断分析

2.1 实验平台搭建与故障模拟

针对船舶推进轴系等效特征搭建轴系故障模拟实验平台如图1所示。

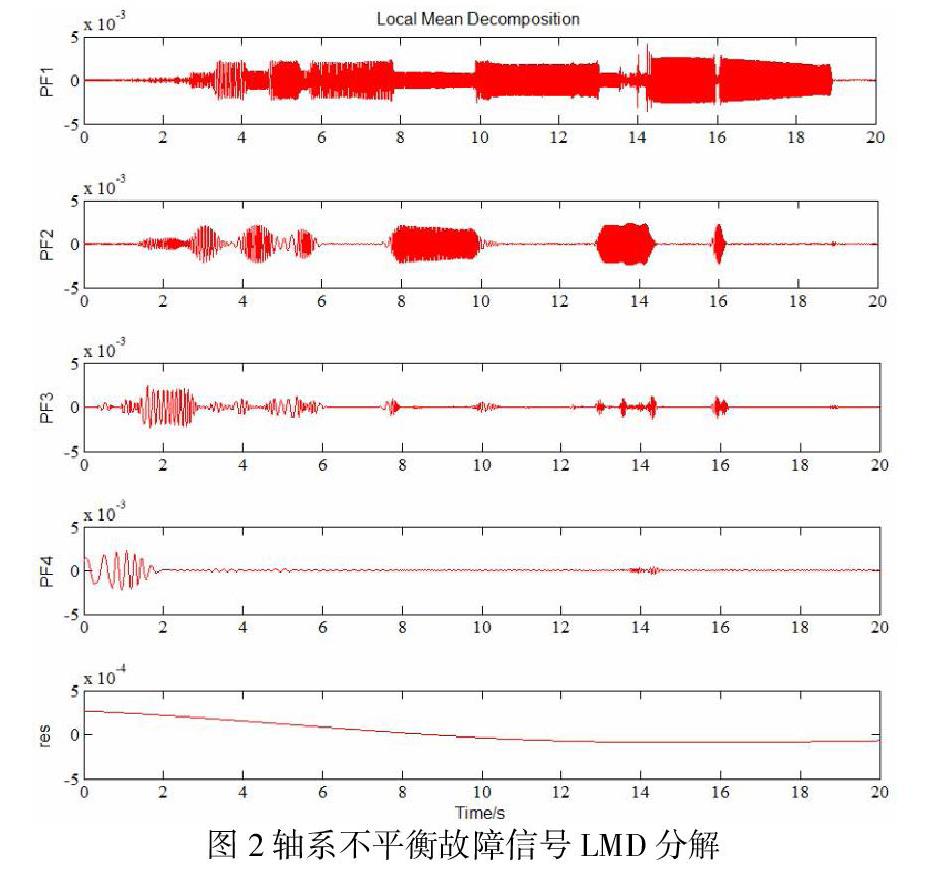
将台架由0加速到3000r/min，加速时间为20s，采样率为1000Hz，分别对轴系不平衡、轴系不对中、碰摩故障的非平稳振动信号采集。采集其波形和频谱，对不平衡故障信号进行LMD分解，结果如图2所示。

2.2基于参数化时频熵的故障诊断

通过参数化的时频熵方法计算轴系不平衡、不对中和碰摩故障下的非平稳振动信号时频熵，实验重复三次，形成故障诊断信号库并进行故障诊断实验验证。从表中可以看出轴系不平衡故障下的参数化时频熵数值基本稳定在5.13～5.26，不平衡故障的参数化时频熵都分布在5.2左右，轴系不对中故障分布在6.4左右，碰摩故障分布在8.3左右，无故障工况下参数化时频熵不超过0.13。

重新设置故障，进行基于改进LMD和参数化时频熵的非平稳振动信号故障诊断实验。从表1中可以看出，对重新设置的计算所得的参数化时频熵与参考值完全匹配，成功识别出了轴系不平衡、轴系不对中、碰摩三种轴系故障和无故障。说明使用基于改进LMD时频分析与参数化时频熵的方法，对轴系故障的多分量复合非平稳振动信号进行识别与特征提取，能够实现对轴系故障的识别。

3 結语

将改进的LMD时频分析与参数化时频熵算法结合，提出一种新的多分量复合非平稳振动信号特征提取方法。用仿真信号和实际轴系振动信号对其效果进行验证，并与其他传统方法进行对比。结果显示该方法对多分量复合非平稳振动信号具有较好的特征提取效果，且克服了传统方法中存在的缺点。

参考文献

[1] 武起立. 基于多体动力学船舶柴油机推进轴系轴承润滑研究[D]. 大连海事大学， 2012.

[2] 彭延峰. 自适应最稀疏时频方法及其在旋转机械故障识别中的应用[D].湖南大学，2017.

[3] Smith J S . The local mean decomposition and its application to EEG perception data.[J]. Journal of the Royal Society Interface， 2005， 2（5）：443-454.

[4] 任达千， 杨世锡， 吴昭同， et al. 基于LMD的信号瞬时频率求取方法及实验[J]. 浙江大学学报（工学版）， 2009， 43（3）：523-528.