动态生成下的高中数学概念教学

王红明

高中数学涉及很多的概念，包括向量、函数、数列、导数等，这些概念是学习高中数学知识的重要基础。教学中为使学生牢固掌握、深入理解高中数学相关概念，促进概念教学质量的进一步提升，应注重采取高效的教学方法。其中在动态生成下，能很好地激发学生的学习积极性，使学生参与到数学概念形成中，加深其印象的同时，有助于其更好地理解与掌握。动态生成是指教师与学生、学生与学生相互合作、探究、对话实现新知识的生成。教学中应提高认识，灵活采用多种方法在动态生成下开展概念教学工作。

一、借助熟悉知识进行动态生成

向量是高中数学的重要概念，指既有大小又有方向的量，分为零向量、单位向量、相等向量、平行向量等。高中数学教学中为使学生更好地掌握向量概念，可从学生熟悉的知识切入教学，更好地吸引学生的注意力，激发其思考热情。众所周知，学生在初中阶段已经学习过有关力的示意图，课堂上要求学生回顾力的示意图的三要素以及画法，然后告知学生力的示意图实质上就是一种向量，在此基础上要求学生回顾所学，讨论以下问题：

（1）向量和数量有什么区别与联系？（2）如何表示向量的大小与方向？（3）向量与有向线段有什么区别？

学生在课堂上通过学习教材内容并与其他学生积极讨论，对向量的概念有了全新认识，得知可用表示向量线段的长度表示向量的大小，用有向线段的箭头表示向量的方向。学生通过学习掌握了两个特殊的向量：单位向量、零向量。其中模为1的向量为单位向量，其方向不受限制;零向量的长度为0，方向是任意的。另外，为获得预期的动态生成效果，顺利完成教学目标，可在课堂上为学生展示如下习题，要求学生进行作答，进一步深化其理解，更好地掌握向量这一重要的概念：

给出下列四个命题：①若a=b都是单位向量，则a=b;②零向量的长度为零，方向是任意的;③若a=b，b=c，则a=c;④若a∥b，b∥c，则a∥c;则正确的命题为（ ）。

A.①②         B.①④         C.②③       D.③④

对于①，单位向量是模为1的向量，并没有说明其方向，因此并不能判断两个单位向量是相等的;对于②零向量为长度为零的向量且方向不确定;对于③两个向量相等需要模与方向均相等;对于④零向量与任意不为零的向量平行，b为零向量时不成立。综上可知只有②③正确，正确选项为C。

二、通过自主学习进行动态生成

学生对函数并不陌生。在初中阶段已较为系统地学习过一次函数、二次函数、反比例函数等，但高中阶段对函数重新进行了定义，而且涉及的内容较为抽象，学习难度较大。为使学生牢固掌握、深入理解函数這一概念，应注重鼓励学生开展自主学习活动，通过动态生成鼓励学生自己进行归纳、总结，在其头脑中留下深刻的印象。一方面，围绕函数概念认真编写导学案，明确学生自主学习的目标、步骤、要求等，在课堂上分发给学生，必要情况下还可录制一些微课视频，在课堂上播放给学生观看。另一方面，专门留出一定的时间，鼓励学生相互交流学习心得，最终在教师的引导与启发下，学生顺利总结出了函数的概念。

学生通过自主学习参与到函数概念的动态生成过程中，从集合角度更加深刻的认识了函数的定义域、值域、对应关系三要素，而且学会了函数的表示方法，很好地增强了学生学习的自信。为使学生更好地理解函数的三要素，课堂上可向学生展示如下习题，要求学生根据自己的理解进行判断，并说出判断理由。

判断下列对应关系是否为集合A到集合B的函数：①A=R，B={x|x>0}， f：x→y=|x|;②A=Z，B=Z， f：x→y=x2;③A=Z，B=Z， f：x→y=;④A={-1，1}，B={0}， f：x→y=0;

该题目重点考查了对函数概念的理解程度。分析时需要学生认真回顾函数的概念，牢牢把握函数概念中的一些关键词，如非空集合、对应关系、任何一个等。对于①，集合A中的元素0，在集合B中无法找到对象，不是函数;由函数概念可知②是函数。③不是函数，如集合A中的2这个元素，无法在集合B中找到对象。④为函数。

三、借助课堂互动进行动态生成

数列是高中数学重要组成部分，包括很多概念，如数列、项、通项公式等，其中数列概念本身并不难记忆与掌握，指按一定的次序排列的比系列数。但要想应用数列中的一些概念，灵活解答相关习题并非易事。其中通项公式在数列中占有重要地位，教学中为使学生能够深刻理解，并能灵活求解数列的通项公式，应通过课堂互动在动态生成下完成教学工作。

课堂上可围绕以下问题学生进行互动：（1）数列有哪些表示方法？（2）怎样用解析式进行表示？（3）数列项公式描述的是谁和谁的关系？（3）怎样求解数列的通项公式？

学生积极回答教师的问题，课堂气氛变得十分活跃，提升了学生的学习体验。在回答问题过程中，学生逐渐认识与掌握了数列通项公式这一概念，但一些学生不知道怎样求解通项公式。课堂上围绕某一具体的数列，继续与学生互动，并为围绕一下例题，为学生示范求解数列通项公式的具体过程，最终学生掌握了求解数列通项公式的一般思路与方法：

已知数列{an}的前n项和Sn=2n2-3n，则数列{an}的通项公式an= ;若其前n项和Sn=3n+1，则数列{an}的通项公式an= 。

所谓数列通项公式是指表示数列第n项an和n之间的关系的公式。根据通项公式求解方法可知，当数列的前n项和为Sn=2n2-3n时，当n=1，a1=S1=2-3=-1;当n≥2时，an=Sn-Sn-1=（2n2-3n）-【2（n-1）2-3（n-1）】=4n-4，a1也适合上式，其通项公式an=4n-5;当数列的前n项和为Sn=3n+1时，当n=1，a1=S1=3+1=4;当n≥2时，an=Sn-Sn-1=3n+1-3n-1-1=2·3n-1，当n=1时不适合上式，因此，通项公式an=4，n=12·3n-1，n≥2 。

四、借助问题情境进行动态生成

导数是高中数学的重要概念，是各类测试考查的重要知识点。教学中为使学生深入的理解导数概念，并能灵活运用，可创设学生熟悉的问题情境，通过动态生成完成这一概念的教学。

考虑学生已学的物理知识，创设以下问题情境，要求学生思考、作答：已知自由落体运动方程为S=gt2，求落体在t0到t0+△t这段时间内的平均速度以及在t0时的瞬时速度。根据所学的物理知识，学生不难求出落体在该时间短内的平均速度=g（2t0+△t），而瞬时速度为在t0→0的极限，显然在t0的瞬时速度v=gt0。从函数角度来看，瞬时速度就是位移函数对时间的瞬时变化率，即函数y=f（x）在x=x0处的瞬时变化率，即为函数y=f（x）在x=x0处的导数。

教学中通过创设学生熟悉的问题情境进行动态生成，学生不仅掌握了导数的概念，而且对其导数概念的理解更为深入，尤其为巩固学生所学，课堂上要求学生思考、解答以下习题，结果学生成功得出正确结果，顺利完成了教学目标：

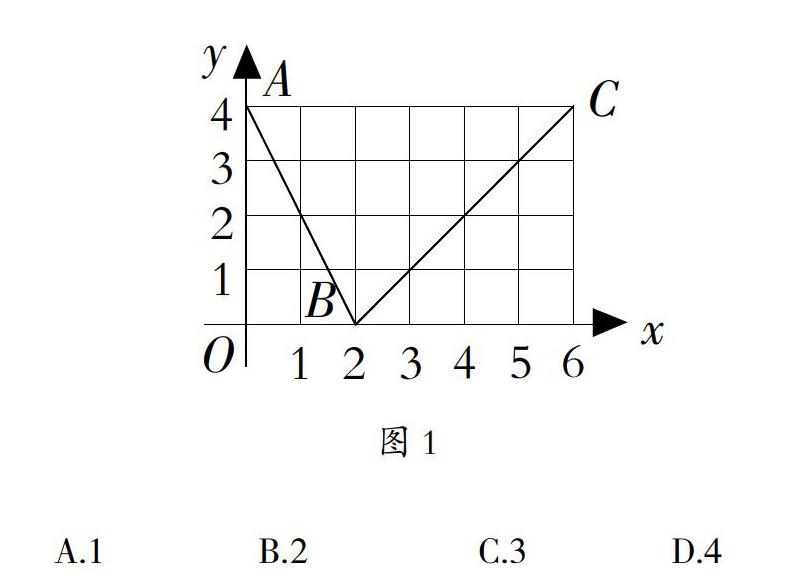
如下图所示，函数f（x）的图像是折线ABC，其中A、B、C的坐标分别为（0，4）、（2，0）、（6，4），那么=（   ）。

A.1                 B.2                   C.3                D.4

该题目灵活考查了导数的概念，只有深入理解导数表示的几何含义，才能顺利求解出该题。很多学生粗心大意，错误的选择了B项。事实上，题目要求的是函数y=f（x）在x=x0處的瞬时变化率，即为函数在x=x0处的导数。根据其定义可知题目中要求的并不是在x=3处的导数，需将其拼凑成在x=3处的导数求解， 即

=2=2f '（3）=2×1=2，正确选项为B。

高中数学概念教学中注重动态生成，不仅能很好地提高学生的学习体验，而且能给学生留下深刻的印象，使其更好地掌握诉求概念本质，因此教学中应提高认识，注重相关理论学习，并结合自身教学经验积极组织学生开展动态生成下的概念教学活动，尤其应做好教学效果的总结，精益求精，对相关的教学细节进行适当的优化与调整，使学生在轻松、欢快的课堂氛围中完成数学概念的学习。

■ 编辑/陆鹤鸣