基于自适应奇异值分解无迹卡尔曼滤波算法的车辆质心侧偏角估计

王 姝, 赵 轩, 余 强

(长安大学 汽车学院，陕西 西安 710064)

0 引言

横摆角速度和质心侧偏角是车辆稳定性控制中最重要的两个参数[1,2]。横摆角速度可以通过陀螺仪采集，但是质心侧偏直接测量困难度较大、设备价格高，目前只能通过非接触式的光学传感器进行，例如可同时使用多普勒效应测量法和绝对测量法的Kistler Correvit S-HR双轴光学传感器。但该传感器在车辆速度小于15 km/h以下时精度不足，并且最大可测量的侧偏角为20°。同时其成本高，对运行环境要求高，该传感器主要用于路面条件较好平整路面上，该条件下车辆几乎没有垂直方向运动。因此考虑到以上因素，车辆上对质心侧偏角均采用的是估计器进行实时在线估计。

近年来国内外大量学者都对质心侧偏角的估计进行了研究，主要分为基于运动学和基于动力学的估计方法。基于运动学的估计方法一般忽略车辆纵向加速度的影响，利用车辆质心侧偏角速度和纵向车速、侧向加速度、横摆角速度、道路坡度之间的运动学关系，对车辆参数、轮胎条件和驾驶操作具有较强的鲁棒性[3]。S. CHUNG等人利用ESP系统已有的传感器，利用积分法求取质心侧偏角，并利用道路坡度信息、侧向加速度信息对质心侧偏角进行补偿[4]。但是在多数文献中都提及由于加速度计和陀螺仪存在偏移误差，基于运动方法质心侧偏角估计容易产生漂移，并且质心侧偏角估计值会随着时间的推移积分累积误差不断增大[7-9]。

基于动力学的车辆质心侧偏角估计方法多采用粒子滤波估计、滑模估计、卡尔曼滤波估计等最优状态估计方法实现估计。

粒子滤波是基于蒙特卡洛模拟理论的近似贝叶斯滤波算法，是一种概率统计的方法[5]。且粒子滤波器克服了在计算状态后验估计过程中解析求解困难的问题，并对系统噪声要求低，可以用于具有各类系统噪声的状态量估计，而不仅限于高斯白噪声。但随着质心侧偏角估计迭代次数的增加，大多数粒子的权值会减小到忽略不计的程度，产生退化粒子，并且这些粒子占用了大量的计算资源，造成资源浪费。因此理论上，虽然粒子滤波器的精度也比非线性卡尔曼滤波精度高，但是这是以状态估计器计算量和实时性为代价的。Chu等人利用无迹粒子滤波对轮胎的侧向力、纵向速度、侧向速度、横摆角速度进行估计[6]。Strano等人提出了一种基于状态依赖-里卡提方程(SDRE)的卡尔曼滤波器的非线性估计方法来估计侧滑角[7]。

滑模变结构控制是一种具有控制不连续性的非线性控制器，其在动态过程中根据系统当前的状态(如模型偏差及其各阶导数等)利用高速率的开关控制法，使系统按照预定滑模面的状态轨迹运动，具有快速响应、鲁棒性强、物理实现简单等优点[8-10]。Stéphant 等人提出了基于滑模观测器的车辆质心侧偏角观测方法[11]。Huang 等人提出了一种基于滑模控制(SMC)的光滑变结构滤波器(SVSF)[12]。Chen等人提出了一种降阶滑模观测器(RO-SMO)以减轻计算负担[13]。王健等人以双曲正切行数为切换函数基于滑模观测器估计车辆的质心侧偏角，有效地减弱了符号切换函数易引起的抖振[14]。滑模估计器由于时间滞后开关、空间滞后开关、系统惯性、系统时间纯滞后、空间死区等原因会造成控制系统抖振，抖振会使控制系统不稳定甚至不可用，尤其是对于离散系统。为此研究学者们提出了许多改进型的滑模变结构控制方法，例如基于遗传算法优化的滑模控制器、鲁棒滑模控制器等。但是抖振是不可能完全消除的，只能一定程度上削弱[15]。

卡尔曼滤波能够利用有限的、非直接的、包含噪声的测量信息估计缺失的信息。经过多年的发展，研究人员进一步提出了扩展卡尔曼滤波、无迹卡尔曼滤波、粒子卡尔曼滤波、交互多模型卡尔曼滤波等多种形式的滤波器，不断改进卡尔曼滤波器性能,使其在线性模型、非线性模型、离散模型、连续模型中都具有良好的状态估计效果，成为一种广泛使用的质心侧偏角状态估计方法。Jin等人基于四轮非线性车辆动力学模型分别建立了基于交互多模型无迹卡尔曼滤波(IMM-UKF)和基于交互多模型扩展卡尔曼滤波(IMM-EKF)的侧偏角估计器[16]。Kim等人采用扩展卡尔曼滤波对车辆的质心侧偏角进行估计[17-18]。Doumiati等人对基于EKF和UKF的车辆质心侧偏角估计器进行了性能对比[19]。Strano等人提出了一种有约束无迹卡尔曼滤波算法，测量噪声以提高估计模型的鲁棒性，避免对车辆的数学模型进行局部线性化，并充分考虑了状态边界[20]。Liu等人提出了一种基于数据融合方法的自适应无迹卡尔曼滤波器(AUKF)来估计系统状态，以提高估计器的鲁棒性[21]。

一些研究人员提出了新的估计方法，使用新的传感器和技术，如差分GPS、雷达、相机和高清地图。Bevly等人利用一个GPS天线和一个惯性导航系统，根据GPS提供的航向角和惯性导航系统提供的车辆横摆角直接估计质心侧偏角[22]。Li 等人还将差分GPS(DA-GPS)与其他低成本的车辆传感器信息相融合利用EKF进行估计[23]。Yoon 等人提出了一种综合陀螺仪、全球定位系统(GPS)和惯性测量单元(IMU)的方法，同时为了抑制陀螺仪的干扰，设计了双卡尔曼滤波器[24]。Botha等人分别利用单摄像机和双摄像机提出了3种基于摄像机图像的质心侧偏角测量方法[25]。但3种基于摄像机图像的质心侧偏角估计方法计算量大，并且在选择测量用摄像头时需要均衡系统精度和运行参数的需求。Jiang 等人提出了一种基于开放街道地图和惯性传感器融合的新方法来估计和预测车辆运动状态[26]。但是考虑到成本问题以及GPS信号在隧道、树荫等遮蔽物附近信号弱甚至信号丢失及估计器运算量的问题，上述方法实用性并不高。

通过对现有车辆质心侧偏角估计方法进行对比，针对无迹卡尔曼滤波(Unscented Kalman Filter，UKF)在系统强非线性或状态模型不精确的情况下，存在状态估计精度降低甚至发散的问题，本研究提出一种基于自适应奇异值分解无迹卡尔曼滤波算法(ASVD-UKF)的车辆质心侧偏角估计方法。该算法采用奇异值分解方法改进无迹卡尔曼率波中状态协方差矩阵的迭代，保证协方差矩阵的非负定性及迭代的稳定性。同时采用自适应因子平衡动力学模型信息与观测信息的权重，控制动力学模型误差对系统状态估值的影响，以改进UKF中状态协方差矩阵的迭代稳定性及估计器的鲁棒性。

1 基于自适应奇异值分解无迹卡尔曼滤波的质心侧偏角估计

1.1 二自由度非线性车辆动力学模型

尽管二自由度线性模型具有计算速度快、计算量小等优点，但是轮胎在非线性区工作与工作在线性区性能有极大的区别。质心侧偏角作为车辆稳定性控制中关键参数，对于它的估计应尽量精确，以保证整个稳定性控制系统的控制精度，因此采用二自由度非线性车辆动力学模型作为估计模型[27]。

图1 车辆二自由度模型

车辆二自由度模型如图1所示。对二自由度车辆模型进行受力分析可得：

(1)

(2)

通过变形可以得到：

(3)

(4)

式中，u为车辆纵向速度；v为车辆侧向速度；a，b分别为前、后轴到车辆质心的距离；m为整车质量；ωr为车辆横摆角速度；δf为前轮转角；β为车辆质心侧偏角；Fy1，Fy2分别为前后轮轮胎侧向力；Iz为车辆绕z轴的转动惯量。

Fy1，Fy2可以利用利用魔术公式MF5.2轮胎模型进行求取，如式(5)所示。

(5)

式中，α为轮胎侧偏角；Fy为轮胎侧向力；Shy和Svy为水平偏移和垂直偏移，以弥补轮胎帘布层转向效应、侧偏离作用或滚动阻力引起的偏移；Cy为形状因子；Dy为峰值因子；By为刚度因子；Ey为曲率因子。由于魔术公式轮胎模型属于经验模型，因此模型中的参数(除Cy以外)都可利用试验数据采用多项式拟合方法获得。

整理可得基于自适应奇异值分解无迹卡尔曼滤波质心侧偏角估计器的状态方程如式(6)所示。

(6)

式中，u为车辆纵向速度；a，b分别为前、后轴到车辆质心的距离；m为整车质量；ωr为车辆横摆角速度；δf为前轮转角；β为车辆质心侧偏角；Fy1，Fy2分别为前后轮轮胎侧向力;Iz为车辆绕z轴的转动惯量。

基于无迹卡尔曼滤波质心侧偏角估计器的测量方程如式(7)所示。

(7)

式中，m为整车质量；ωr为车辆横摆角速度；δf为前轮转角；β为车辆质心侧偏角；ωr为车辆横摆角速度；ay为车辆侧向加速度；Fy1，Fy2分别为前后轮轮胎侧向力；Iz为车辆绕z轴的转动惯量。

将基于自适应奇异值分解无迹卡尔曼滤波的质心侧偏角估计器的状态方程和测量方程表达为标准的状态方程，如式(8)所示：

(8)

式中，X=[β,ωr]T,y=[ay,ωr]T；ωk∈N(0,Qk)、vk∈N(0,Rk)分别为系统观测噪声和测量噪声，且均为高斯白噪声。

1.2 基于自适应奇异值分解无迹卡尔曼滤波算法

为了改善UKF中状态协方差矩阵迭代的非负定性及稳定性，增强估计器的鲁棒性，提出了基于自适应奇异值分解无迹卡尔曼滤波算法。具体建立步骤如下：

(9)

(10)

(2)构建Sigma点。

常见的Sigma点构建方法包括一般型无迹变换、单形无迹变换、球形无迹变换等。本研究采用对称采样方法生成2n+1个Sigma点。在利用UT变换产生Sigma点时需要对方差矩阵P进行分解，常见的矩阵分解方法包括：Cholesky分解、SVD分解、QR分解、Jordan分解[28]。

① 基于Cholesky分解的Sigma点构建

对随机变量Xk-1的协方差矩阵Pk-1进行Cholesky分解，如式(11)所示。

(11)

式中，Lk-1为Cholesky分解的正定下三角矩阵。

则经过Cholesky分解,得到了Sigma点矩阵χk-1(i=0,1,2,…，2n)如式(12)所示。

(12)

因此

χk-1=(χ0,k-1,χ1,k-1,χ2,k-1,…,χn,k-1,χn+1,k-1,…,

(13)

λ=α2(e+κ)-e，

(14)

② 基于SVD的Sigma点构建

由于观测粗差、迭代计算过程中的截断误差和状态模型扰动等会造成式(11)中的方差矩阵Pk-1失去对称正定性，而无法使用Cholesky进行分解。奇异值分解(SVD)是数值稳定和精度较高的一种矩阵分解算法，其突出的优点是不需要被分解矩阵是对称正定矩阵。本研究采用SVD分解方法进行Sigma点的构建。

对方差矩阵Pk-1进行SVD分解，如式(15)所示。

(15)

式中，Uk-1、Vk-1列向量分别为方差矩阵Pk-1的左右奇异向量；Λ为方差矩阵Pk-1奇异值矩阵。

则经过SVD分解得到的Sigma点矩阵如式(16)所示：

因此

(17)

(3)时间更新

χk|k-1=f(χk-1,Uk)+Wk，

(18)

(19)

(20)

(21)

式中，αk为自适应因子。

(22)

进一步利用自适应因子对奇异矩阵进行修正，得到新的Sigma点及先验估计误差的协方差矩阵，如式(23)，式(24)所示。

(23)

(24)

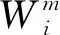
(25)

(4)测量更新

利用测量方程对各Sigma点进行非线性变换。

(26)

(27)

测量值协方差更新如式(28)所示。

(28)

估计值和测量值协方差更新如式(29)所示。

(29)

状态量的更新如式(30)～(32)所示。

(30)

(31)

(32)

2 试验验证

2.1 试验平台的构建

本研究基于双电机驱动电动试验车，利用AD5435硬件在环仿真系统和MATLAB/simulink代码自动生成技术搭建了双电机驱动电动汽车试验平台，对基于自适应奇异值分解无迹卡尔曼滤波算法的车辆质心侧偏角估计算法进行验证。试验平台的搭建包括硬件开发和软件开发两部分。采用AD5435作为车辆的整车控制器，控制器输入信号包括：方向盘的转角、角速度、扭矩，加速踏板角度，制动踏板角度，车速，轮速，电机扭矩，电机功率等。输出信号包括：电机驱动扭矩、电机制动扭矩、液压制动系统制动扭矩。上述输入信号可以通过如下传感器获得：使用安装在转向柱上的方向盘扭矩、角度传感器采集方向盘转角、方向盘角速度、方向盘扭矩；使用霍尔式非接触速度传感器采集4个车轮的转速；采用Passat B5双路加速踏板传感器采集加速踏板角度；采用制动踏板传感器采集制动踏板角度；采用三轴陀螺仪采集车辆的纵向加速度、侧向加速度、横摆角速度；电机转速、扭矩、功率信息可以从电机控制器的CAN信号中获取。试验平台中传感器性能参数如表1所示。

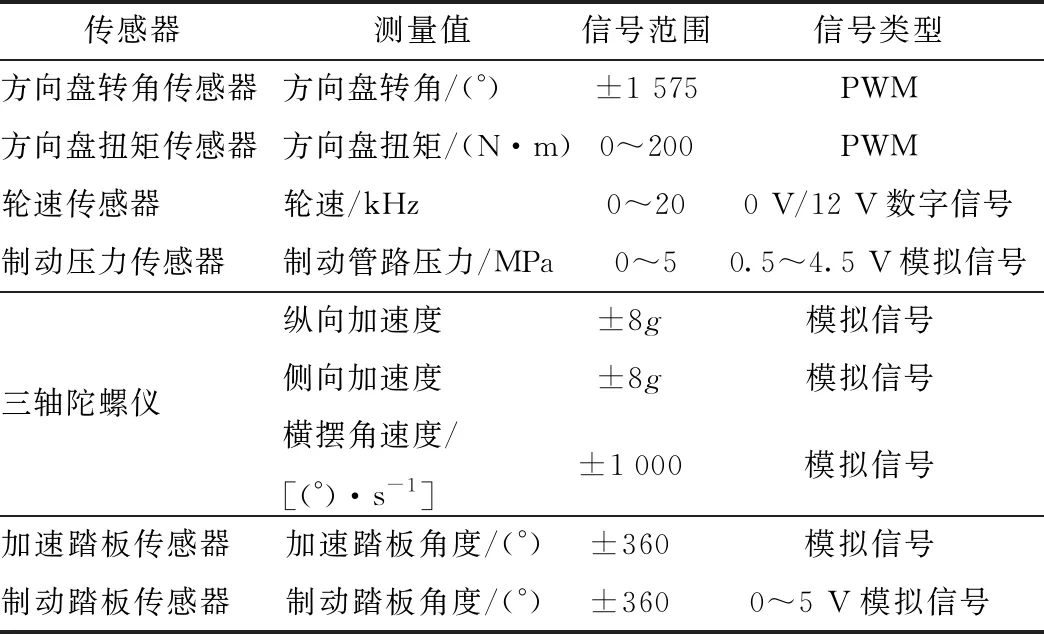
表1 传感器性能参数

同时还需要根据各传感器输出信号的特性，选取合适的板卡。选取A&D5430-01 16路16位模拟量输入板卡用于采集加速踏板传感器、制动踏板传感器、电流传感器信号、三轴陀螺仪信号、方向盘扭矩信号；选取A&D5430-03 32通道数字量输入/输出板卡采集轮速传感器信号；选取A&D5430-17 4通道CAN通讯板卡采集两台电机控制器信号，并向电机控制器输出扭矩指令；选取A&D5430-13 28通道PWM输入/输出板卡采集方向盘角度、角速度信号。

表2 整车基本参数

之后对板卡的Simulink模型进行设置，利用基于Matlab/Simulink的Real-time Workshop(RTW)技术，对模型、板卡设置模型等进行编译，利用ModelDef软件对模型的输入、输出及观测点进行定义；利用VistualConsole对上位机及A&D5435显示屏GUI进行设计，并将编译好的程序下载到A&D5435中，完成试验平台软件部分开发。基于A&D5435的双电机驱动电动汽车试验平台如图2所示。

实车试验是在长安大学车辆综合性能试验场的操稳性广场上进行的，利用建立的分布式驱动电动汽车硬件在环平台对基于ASVD-UKF的质心侧偏角估计器进行验证,并与基于无迹卡尔曼滤波的车辆质心侧偏角估计器进行对比，验证质心侧偏角估计器的准确性。为此本研究分别在双移线工况、单移线工况下进行试验验证。

图2 基于A&D5435的双电机驱动电动汽车试验平台

(1)双移线试验

试验选择在ISO 3888-1标准双移线工况下进行，如图3所示为目标行驶路径。图中，d1=1.1L+0.25，d2=1.3L+0.25，L为车宽。试验道路路面附着系数为0.4。首先驾驶人应使车辆与行驶道路保持水平，并且使方向盘位于中间位置；随后驾驶员操纵车辆在道路上加速直行，使得车辆进入双移线道路的初始车速为60 km/h，期间应不操纵方向盘使得方向盘保持在中间位置，之后驾驶员根据路面的锥桶标记自由行驶。如图4所示为ASVD-UKF 估计器、UKF估计器和试验获得质心侧偏角，如图5所示为试验过程中车辆的侧向加速度。

图3 双移线工况轨迹

图4 车辆质心侧偏角曲线

图5 车辆侧向加速度曲线

双移线工况下基于自适应奇异值分解无迹卡尔曼滤波算法和无迹卡尔曼滤波算法估计得到的车辆质心侧偏角最大误差、平均误差及均方根误差如表3所示。

由表2可知，UKF算法最大误差为1.622 4°，误差较大处主要位于侧向加速度峰值处。ASVD-UKF算法的最大误差为1.297 8°，减小了20.01%。ASVD-UKF算法的平均误差为0.015 2°，UKF算法平均误差为-0.077°，减小了80.26%。ASVD-UKF算法的均方根误差误差为0.357 2°，UKF算法均方根误差为0.445 7°，减小了19.86%。图5为车辆运行过程中的车辆侧向加速度曲线，整个过程中车辆的侧向加速度最大值达到-0.460 4g。一般普遍认为当车辆侧向加速度小于0.4g时，轮胎工作在线性区域，但在峰值处车辆的侧向加速度为0.482 3g，轮胎已经工作在非线性特征区域，但由于采用的是二自由度非线性车辆动力学模型，模型已经充分考虑了轮胎的非线性特征，因此质心侧偏角估计器在此工况下仍能良好估计。

表3 双移线工况车辆质心侧偏角最大误差、平均误差及均方根误差

(2)单移线试验

试验工况选择在SAE J2179—2000标准单移线工况进行，试验道路如图6所示。图中h=3.5 m，b=1.2L+0.25 m，L为车宽，d1=50 m，l2=100 m，l3=15u(u为纵向车速)。首先驾驶人应使车辆与行驶道路保持水平，并且使方向盘位于中间位置；随后驾驶员操纵车辆在道路上加速直行，使得车辆进入单移线道路的初始车速为50 km/h，期间应不操纵方向盘使得方向盘保持在中间位置，之后驾驶员根据路面的锥桶标记自由行驶。如图7所示为ASVD-UKF估计器、UKF估计器和试验获得质心侧偏角，如图8所示为试验过程中车辆的侧向加速度。

图6 单移线工况轨迹

图7 车辆质心侧偏角曲线

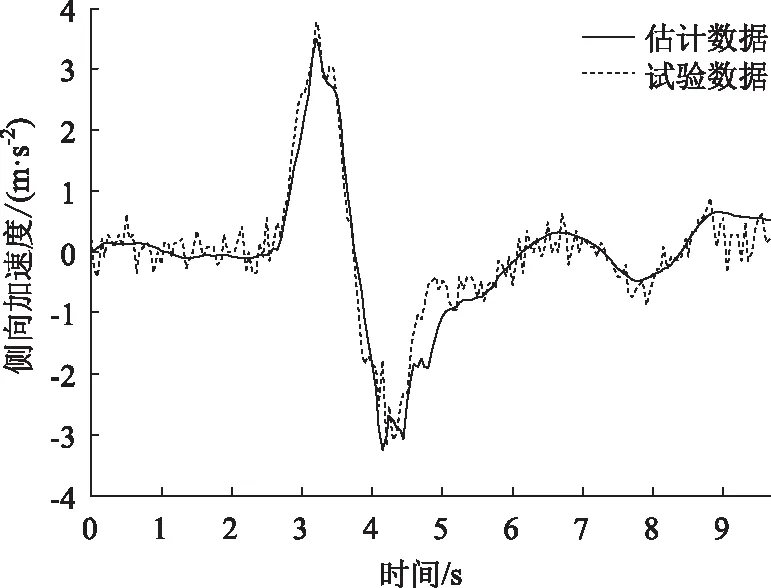
图8 车辆侧向加速度曲线

单移线工况下基于自适应奇异值分解无迹卡尔曼滤波算法和无迹卡尔曼滤波算法估计得到的车辆质心侧偏角最大误差、平均误差及均方根误差如表4所示。

表4 单移线工况车辆质心侧偏角最大误差、平均误差及均方根误差

UKF算法最大误差为1.322 2°， SVD-UKF算法的最大误差为1.021 7°，减小了22.27%。SVD-UKF算法的平均误差为-0.105 8°，UKF算法平均误差为0.036 5°，减小了65.5%。SVD-UKF算法的均方根误差误差为0.240 8°，UKF算法均方根误差为0.385 4°，减小37.52%。如图8所示为车辆运行过程中的车辆侧向加速度曲线，整个过程中车辆的侧向加速度最大值为-0.462 8g，因此基于奇异值分解无迹卡尔曼滤波算法的质心侧偏角估计器可以在车辆线性状态下良好工作。

根据上述仿真结果，基于ASVD-UKF算法的质心侧偏角估计方法在典型车辆稳定性测试工况-双移线工况、单移线工况下能够准确估计出车辆的质心侧偏角，估计平均误差、最大误差及误差的均方根值均明显小于基于UKF算法的估计器，估计精度优于基于UKF算法估计出的质心侧偏角估计器。因此，可以认为基于ASVD-UKF算法的车辆质心侧偏角估计器精度更高，能够满足车辆稳定性控制的要求。

3 结论

(1)通过对现有车辆质心侧偏角获取方法进行分析，利用自适应奇异值分解方法构建sigma点，并在时间更新过程中利用自适应因子对奇异矩阵进行修正，改进了 UKF 中状态协方差矩阵的迭代的稳定性及估计器的鲁棒性。

(2)利用分布式驱动电动汽车半实物仿真平台分别在双移线工况、单移线工况下对基于UKF和ASVD-UKF算法的质心侧偏角估计方法进行了对比验证。与 UKF估计结果的平均绝对误差和均方根误差的比较表明基于ASVD-UKF的估计器性能优于基于UKF的估计器；与真实值对比表明，ASVD-UKF算法精度高，能够满足车辆稳定性控制的需要。