带有丢失数据补偿的高速公路入口匝道MFAC方案
2020-12-28闫帅明卜旭辉朱盼盼许漂漂
闫帅明,卜旭辉,朱盼盼,许漂漂
(河南理工大学 电气工程与自动化学院,河南 焦作 454000)
0 引言
目前,城市高速公路是现代城市地面交通系统的重要组成部分之一。它被用于居民在城市快速旅行,提高车辆效率并有一定的可靠性[1-3]。然而,随着经济的发展,车辆保有率的增高,快速公路承受越来越大的交通压力[4]。入口匝道控制是高速公路交通控制中最有效的控制方法之一。目前有许多关于高速公路的先进控制算法,如时序控制算法[5],感应控制算法[6-7],迭代学习控制(ILC)[8],ALINEA控制算法[9-11]和瓶颈路段匝道控制算法[12]等。通过建立高速公路精确交通流模型的方法,针对入口匝道的控制已有很多研究结果。其中文献[13]基于交通流模型,利用遗传算法提出具有递归环节的动态模糊神经网络实现城市高速公路的入口匝道智能控制,并通过仿真对比验证了算法优越性;文献[14]通过使用模型预测的方法,以平均速度为控制标准提出了多交通的协同控制方案,并通过仿真验证该方案的有效性。在精确的高速公路交通流模型下,上述方案对高速公路控制达到了期望控制效果。
由于高速公路系统结构复杂,道路中行驶车辆的交通机制有所不同,难以用精确的模型描述系统的运行特性。而且,现代高速公路交通控制系统在控制中心和执行器之间传输交通流量输入数据时,可能会由于网络控制中网络拥塞、通信冲突和连接中断等现象造成交通控制中的数据丢失,最终影响控制效果。上述文献大多基于精确交通流模型进行控制且未考虑高速公路网络控制系统中存在的数据丢包问题。
考虑上述问题,本研究基于宏观交通流模型和一般非线性系统无模型自适应控制[15](MFAC)方案,提出了一种在数据丢失的情况下具有丢失数据补偿的MFAC方案。针对在高速公路入口匝道网络控制中存在的随机数据丢包问题,首先,将高速公路车流量密度数据丢失现象描述为取值0/1的伯努利序列,并提出仅利用系统输入和数据丢包下输出数据构造的控制器。其次,考虑到数据丢失对系统控制性能的影响,进一步设计了数据丢失补偿算法。最后通过MATLAB仿真表明,该方案能保证在数据丢失下高速公路输出密度收敛于期望值。
1 系统模型和问题描述
1.1 系统模型
交通流模型描述了随着时间的变化交通流状态变量和交通控制变量之间的关系。宏观动态交通流模型可以准确地描述高速公路各段的交通状况[16]。
本研究采用Papageorgiou[17]提出的宏观交通流模型。图1为高速公路段的划分示意图。
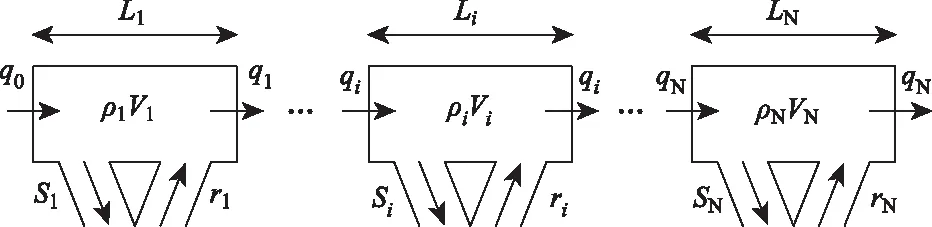
图1 高速公路各路段示意图
快速道路宏观交通流模型的离散化可以如下表示:
(1)
qi(t)=ρi(t)vi(t),
(2)
(3)
(4)
式中,t∈{0,1,…,k}为第k个采样间隔;i∈{1,…,N}为第i个高速公路路段;N为路段的总数;ρi(t)为在第k个时段,路段i上交通流的平均密度;vi(t)为在第t个时段,路段i上车辆的平均速度;qi(t)为在第t个时段,从路段i到路段i+1的交通流量;ri(t)为入口匝道流量,指在第t个时段从入口匝道进入路段i的交通流量;si(t)为出口匝道流量,指在第t个时段从出口匝道驶出路段i的交通流量;Li为高速公路路段i的长度;vf为自由流速度(当车辆密度为零时车辆的最大允许速度);ρm为临界密度,即该路段的最大车流密度;T为采样周期;τ,γ,κ,l,m为常数,为交通特定参数。
注1:模型满足当车辆以最大速度通过检测区域时所用的时间应该小于等于采样周期。即,T≤Lmin/vf,其中Lmin为检测区域的最小值。
假定在第t个到第t+1个采样时间内进入第1个路段的车流量为q0(t),车辆的平均速度等于第1个路段上车辆的平均速度,即v0(t)=v1(t),且进入第N+1个路段的车辆平均速度和密度分别等于路段N上平均速度和密度,即:
vN+1(t)=vN(t),ρN+1(t)=ρN(t)。
(5)
那么,上述高速公路交通流模型的边界条件可归纳为:
ρ0(t)=q0(t)/v1(t),
(6)
v0(t)=v1(t),
(7)
ρN+1(t)=ρN(t),
(8)
vN+1(t)=vN(t)。
(9)
通过上述的模型描述发现,在以缓解交通拥堵的目的下,可以通过限制高速公路入口匝道的车流量来达到控制目的。即,在数学描述中,以入口匝道流量ri(t)为系统的控制输入信号、该路段的车流密度ρi(t)为系统的输出信号。
根据式(1)~(4),高速公路系统第i个路段的非线性离散时间模型如下表示:
ρi(t+1)=f[ρi(t),ri(t)],
(10)
式中f(…)为未知非线性函数。
假设1 除有限时间点外,f(…)关于第2个变量的偏导数是连续的。
假设2 非线性函数f(,)满足全局Lipschitz连续条件,|ρi(t+1)-ρi(t)|≤b|ri(t)-ri(t-1)|,其中b>0。
1.2 问题描述
现代高速公路交通控制系统可用于在现场数据获取单元和控制中心之间传输交通流量输出数据,并在控制中心和执行器之间传输交通流量输入数据。但是,在网络控制中网络拥塞、通信冲突和连接中断等现象是不可避免的,最终导致交通数据丢失。交通数据的丢失将直接影响控制中心对交通系统的控制效果。
由于在本研究交通流密度ρi(t)为控制输出,所以在网络中密度将是控制中心与控制现场之间传递的主要数据。因此,考虑输出的车辆密度ρi(t)在网络传输过程中出现丢包现象,并假设道路交通控制器可以实时监测到高速公路车辆密度是否丢失。本研究将车辆密度数据丢失现象描述为概率已知的伯努利序列[18]α(t),当系统检测到交通流密度数据丢失时α(t)取值为0,否则α(t)取值为1,其定义为:
(11)
由此,本研究的控制目标是,针对式(5),设计合适的控制算法,当测量密度ρi(t)存在部分数据丢失情况时,通过调整输入车辆ri(t)使得输出车流密度能够收敛于期望密度ρd。使控制路段密度能够稳定在期望值附近。
2 控制方案设计
根据上节对问题的描述和控制目标的分析,本节给出具体的控制方案设计。
定理1[15]对于满足假设1和假设2条件的快速交通流量式(5),当|Δri(t)|≠0时有一个称为伪偏导数(PPD)的时变参数φi,c(t)∈R,可以把式(5)转化为以下模型:
Δρi(t+1)=φi.c(t)Δri(t),
(12)
且φi,c(t)为对于任意时刻t收敛。
定理2[15]对于满足假设1和假设2的高速公路式(5),如果存在一个正数t0>1使得:
(13)
那么对于任意t≥t0总可以找到一个有界的整数δ,使得:
(14)
同时存在一个偏导数(PDD)φi,c使得式(5)转换成如下形式:
ρi(t+1)-ρi(t-δt+1)=φi,c(t)[ri(t)-
ri(t-δt)],
(15)
并且对于任意时刻t,φi,c(t)有界。
故系统可以转换成如下数据模型:
ρi(t+1)=ρi(t)+φi,c(t)Δri(t)。
(16)
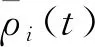
(17)
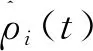
当出现数据丢失时,可以利用式(11)对ρi(t)进行估计,表达如下:
(18)
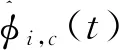
通过以上描述,可以给出在高速公路系统中,出现测量交通流密度丢失情况下带有丢失数据补偿的MFAC方案:
(19)
(20)
(21)
式中λ>0,μ>0,ρ∈(0,1],η∈(0,1],ξ为一个小正数。
该方案的实现流程如图2所示。
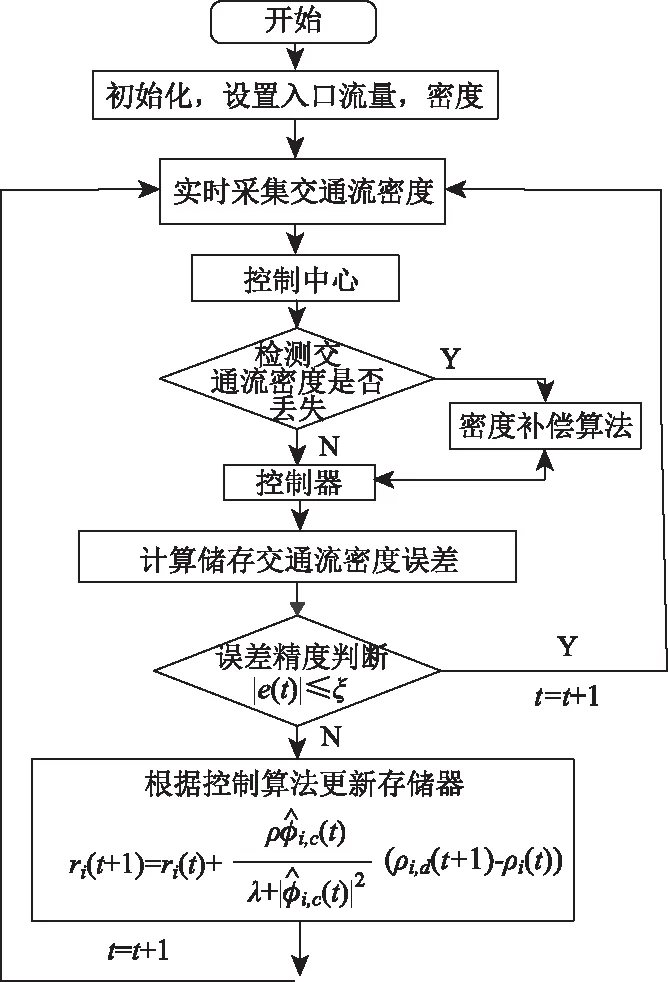
图2 具有数据丢失补偿控制方法流程图
3 收敛性分析
假设3:在高速公路系统中,给定期望密度ρi,d(t+1),总存在一个有界的输入ri(t),使得高速公路系统的输出ρi(t+1)等于期望密度。
ρi(t+1)=ρi,d(t+1)。
(22)
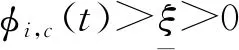
定理3:在满足假设1,假设2,假设3和假设4的条件下,在车辆输出密度丢失的情况下应用方案(14)~(16),当期望密度ρi,d(t)=ρi,d为常值时,则系统的输出误差是收敛的。
对于输出数据丢失时刻kz-1+2有:
(23)
以此,对于输出数据丢失时刻tz-1+1有:
Δri(tz-2)。
(24)
对于数据丢失时刻tz-1 (25) 定义系统跟踪误差为: ei(t)=ρd-ρi(t)。 (26) 利用式(4),式(21)写为: (27) ⋮ (28) 根据上式可推得: (29) 若ei(tz-1)≠0由式(29)可得: Δri(t)≠0, 其中,tz-1 ρi(t)=ρi(t-1)+φi,c(t-1)Δri(t-1) ⋮ =ρi(tz-1)+φi,c(tz-1)Δri(tz-1)+… +φi(t-2)Δri(t-2)。 (30) 将式(29)、(30)代入式(26)得: ei(t)=ei(tz-1)-φi,c(tz-1)Δri(tz-1)-…-φi,c(t-2) Δri(t-2)-φi,c(t-1)Δri(t-1)=ei(tz-1)· (31) (32) (33) (34) 若选择ρ∈(0,1],λ>(b+b1)2/4,可得 (35) 由式(35)可知,存在一个正数d′(t-tz-1),使得: (36) 对式(31)取绝对值,则式(36)可改为: (37) 如上结果可以证明,当输出密度出现丢失的时候,式(19)~(21)能够保证输出误差收敛且有界。 本研究仿真设计一条6 km的单车道高速公路,有12个路段,每个路段的长度为0.5 km,所需密度(期望密度)为ρd=30 veh/km。进入第1段的交通流量是1 500 veh/km。 其中,第4路段有个入口匝道,第7路段有一个出口匝道,入口匝道交通流为r(t)=250+10 sin(t×pi/n),其中n为采样间隔。 表1中列出了每个参数的值和变量的初始值。其中,T满足T≤Lmin/vf。 当在输出数据没有丢失时,MFAC方案用于控制高速公路匝道。其中参数分别为ρ=5,η=0.07,μ=0.09,λ=15,ξ=5×10-5,仿真结果如图3~4所示。 表1 模型参数以及各路段交通流密度和速度的初始值 图3和图4显示了使用MFAC方案时第7路段上数值交通流密度的跟踪误差和跟踪效果。仿真结果表明,随着时间的增加,在没有输出密度丢失的情况下,交通流密度逐渐收敛到期望值。该方案利用高速公路运输系统的输入输出数据,调整入口匝道路段的车流量,使主干道上的交通流密度连续接近所需密度,达到期望的控制效果。 当出现交通流输出密度数据丢失的情况下,使用没有丢失数据补偿的MFAC方案和具有数据丢失的丢失数据补偿的MFAC方案式(19)~(21),研究输出数据丢失率为70%时的跟踪误差和跟踪效果。仿真结果如图5~6所示。 图3 交通流密度的跟踪误差 图4 交通流密度的跟踪效果 图5和图6显示出了当交通流量系统的输出数据丢失率为70%时两种方案下路段7的交通流信息。图5(a)和图6(a)分别为当输出数据丢失率为70%时,没有数据补偿的MFAC方案的跟踪误差和跟踪效果。 图5(b)和图6(b)显示了通过数据补偿获得的跟踪误差和跟踪效果。通过对比发现,在没有改进的算法中,仿真进行到800个采样周期左右跟踪误差可以收敛到零,此时跟踪效果收敛于期密度。在丢失数据补偿的结果中,仿真到500个采样周期时跟踪误差收敛于零,跟踪效果收敛于期望密度。通过对比验证了算法的收敛性和算法的优越性。 图7(a)、(b)显示了当数据丢失率为80%时没有数据丢失补偿的MFAC方案和具有数据丢失补偿MFAC方案的交通流密度跟踪误差。 图8(a)、(b)显示了当数据丢失率为80%时,没有数据丢失补偿的MFAC和具有数据丢失补偿的MFAC的交通流密度跟踪效果。从图7可以看出,在1 300个采样周期左右MFAC方案的跟踪误差收敛于零,跟踪效果收敛于期望密度。在700个采样周期左右改进算法的跟踪误差收敛于零,跟踪效果收敛于期望值。通过对比可知,在任何丢失率下带有数据丢失补偿方案的跟踪误差和跟踪效果要优于普通MFAC方案。 图5 数据丢失70%的交通流密度跟踪误差 图6 数据丢失70%的交通流密度跟踪效果 图7 数据丢失80%的交通流密度跟踪误差 图8 数据丢失80%的交通流密度跟踪效果 从图3~图8可以看出,当系统输出数据丢失时,随时率的增大系统的跟踪误差和密度跟踪效果虽然都能达到收敛但速度会越来越慢,可以看出数据丢失的情况会对系统的稳定造成一定的影响。又通过图5~图8的对比不难看出,该补偿方案很大程度上削弱了数据丢失对控制系统的影响,从结果可以看出该补偿算法已经达到期望效果。 基于宏观交通流模型,将一般离散非线性系统的MFAC方案应用于快速道路交通系统,并通过仿真验证。考虑到高速公路交通控制中的输出交通流密度数据丢失情况,提出了具有丢失数据补偿的MFAC方案。该方案利用MFAC算法内部的伪梯度估计值、输入流量和输出密度历史值构造丢失数据补偿算法对数据丢失时刻交通流密度进行补偿。仿真结果表明,该方案将交通流密度收敛到预期值,而且随着丢失率的增加变化该方案都能达到理想的控制效果。仿真结果验证了该方案的有效性和普遍性。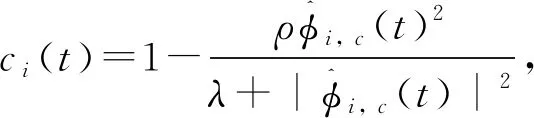
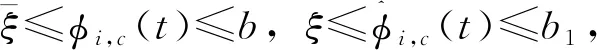
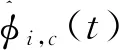
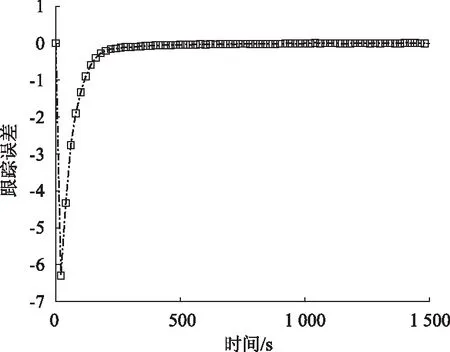
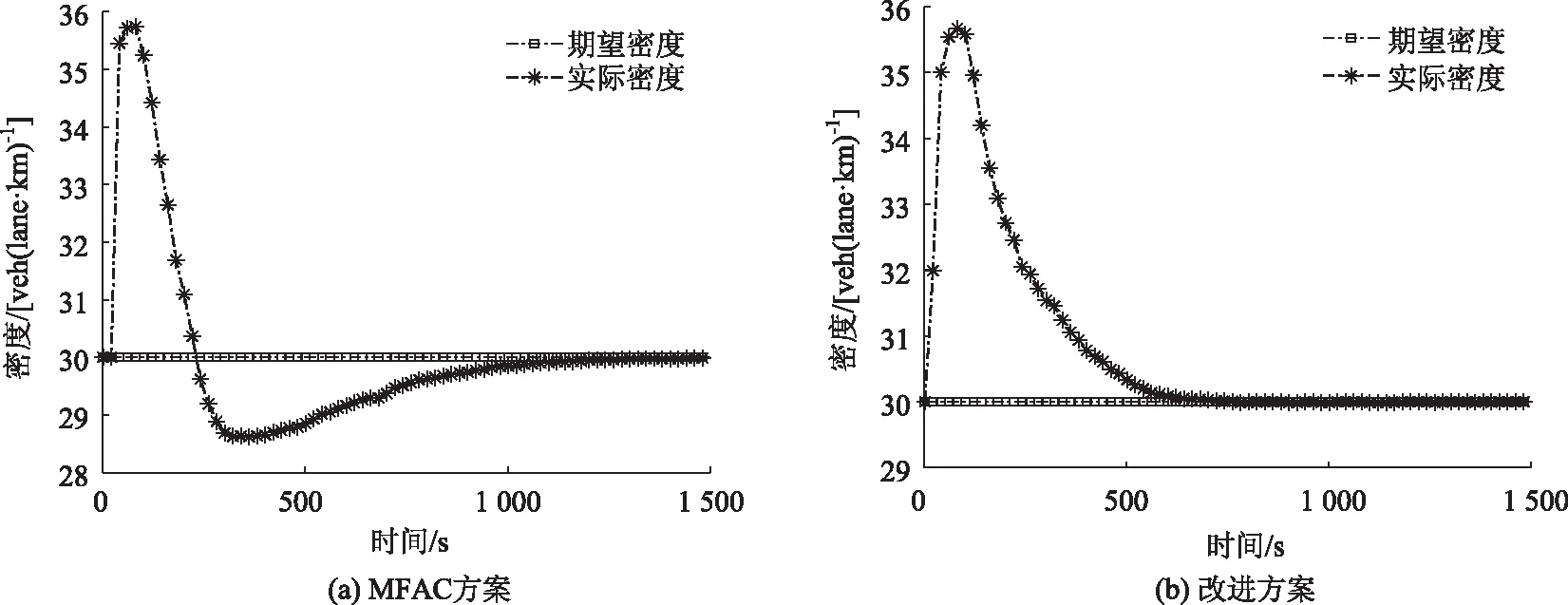
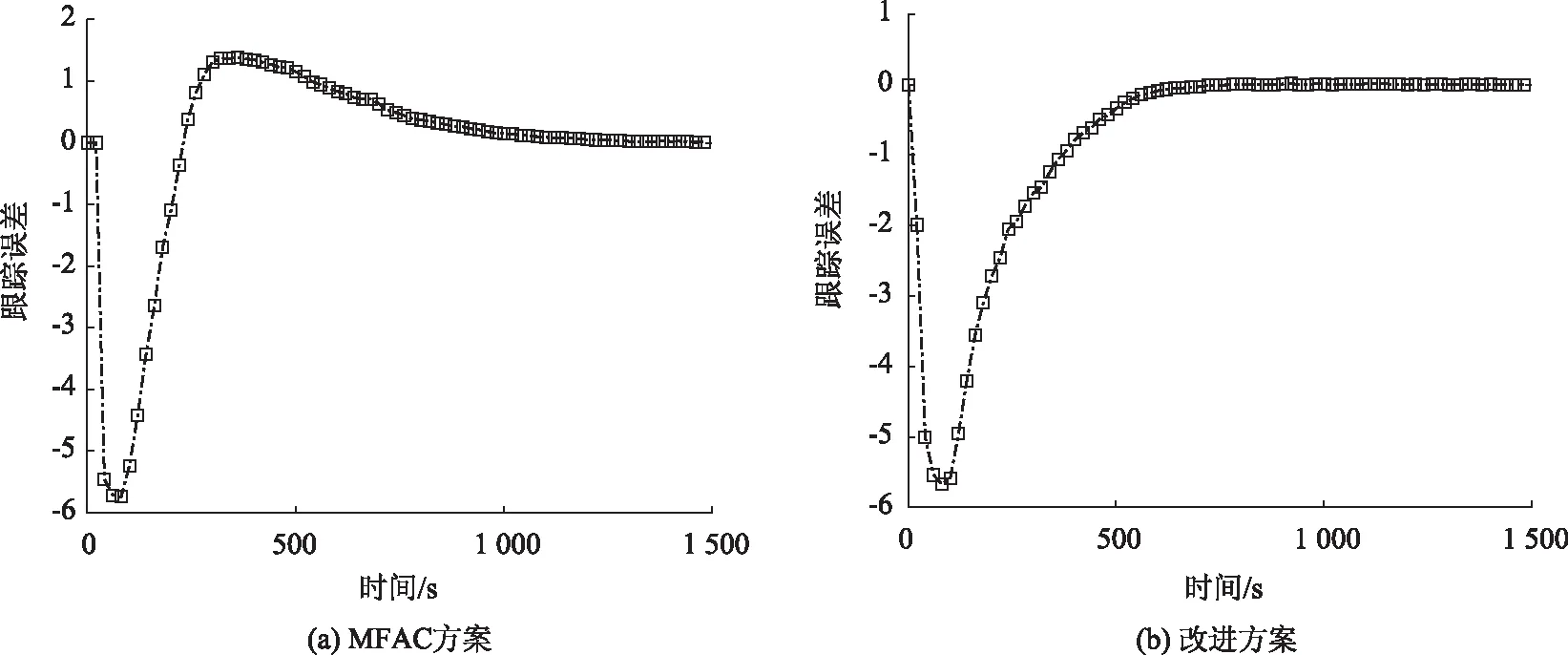
4 仿真研究

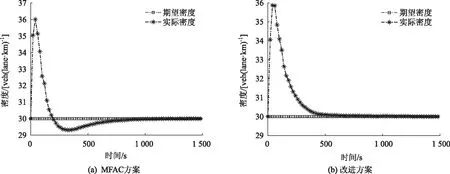
5 结论
